前端程序員必須掌握之三角函數在前端動畫中的應用
作者:HelKyle
原文地址:https://juejin.im/post/5d99b706e51d4577f9285c33
開發(fā)過程中經常有意無意地刻意避開數學相關的知識,你也知道解數學題非常枯燥無趣。平時寫動畫也盡量使用 css3 來實現,timer-function 隨意選用,最多也就調一下 cubic-bezier,找到看著舒服的就行。但是怎樣讓動畫更順滑,寫出更貼近自然的動畫,說實話以前我沒怎么考慮過。
每次當動效設計師提出,能不能這樣那樣的時候,我會理所當然地予以否決。所以有很長一段時間,我非常羨慕那些能用 canvas 繪制很酷炫的動畫的程序員。
先這樣吧,又不是不會動。
今天來分享一下三角函數相關的內容,如果剛學前端的時候有人教我這些,我會很開心。
三角函數
三角函數已經是老生常談了(街舞圈稱之為 Old School),它伴隨我們從初中到大學,太多的公式定理,光是應付考試就花了不少時間。先簡單回顧一下,確保你還記得基礎知識。
勾股定理
最開始學三角函數的時候就是從背勾三股四弦五開始,勾股定理描述的是對于直角三角形,直角兩條邊的平方和等于斜邊的平方。
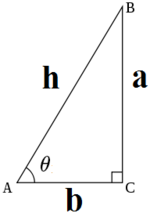
常用三角函數
印象中教科書里面只保留了 sin, cos, tan,其他可以通過變換得到。
sinθ?=?a?/?h
cosθ?=?b?/?h
tanθ?=?a?/?b
極坐標系和單位圓
在笛卡爾直角坐標系中,任一點 (x, y) 都可以轉化成極坐標表示 (r, θ),其中
r?=?Math.sqrt(x^2?+?y^2)
θ?=?Math.atan2(y,?x)
單位圓的定義是半徑為單位長度的圓,圓上任意一點的橫坐標就是對應角度的余弦值,任意點的縱坐標就是對應角度的正弦值。
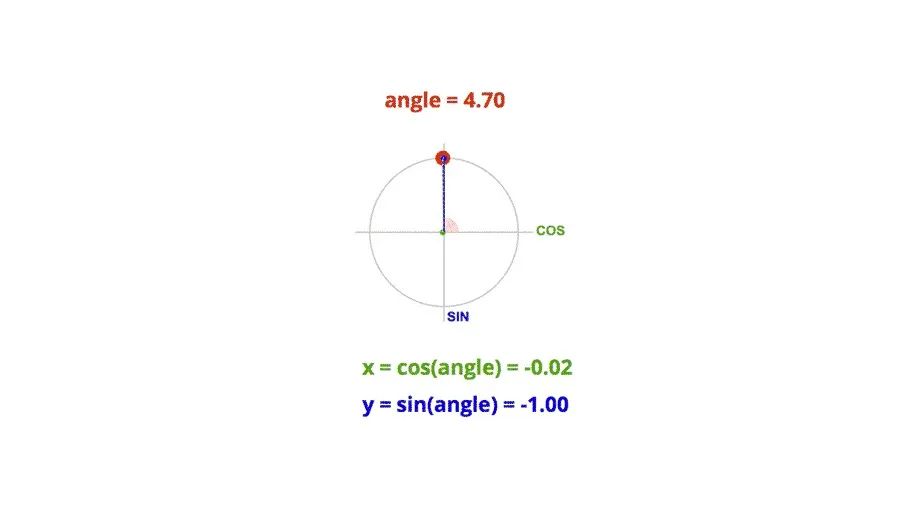
簡單的圖像變換以正弦曲線為例,對函數進行簡單的變換,得到不一樣的結果。
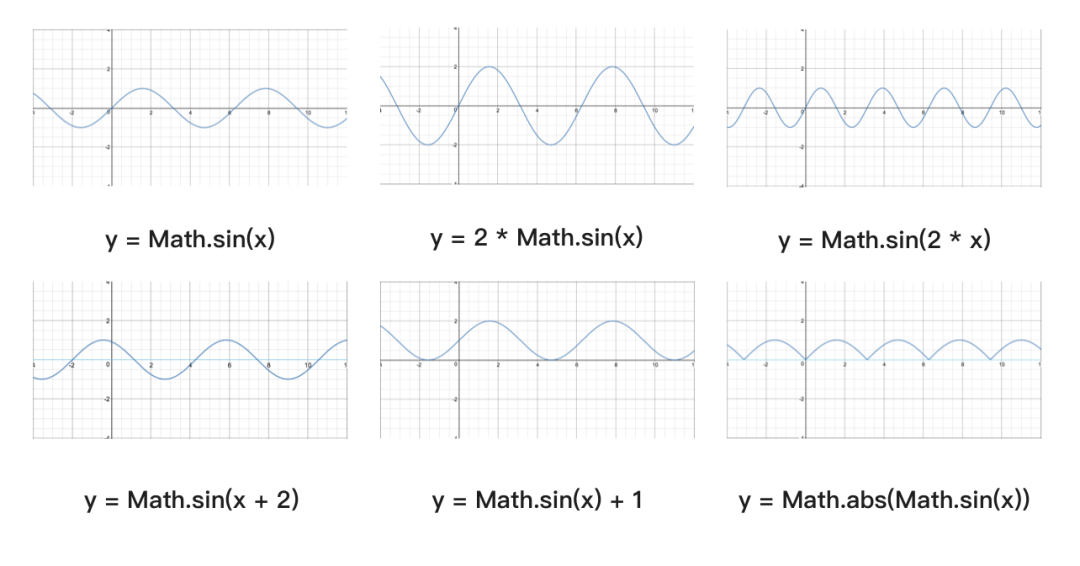
正弦曲線公式:y = A sin(Bx + C) + D
A 控制振幅,A 值越大,波峰和波谷越大,A 值越小,波峰和波谷越小;B 值會影響周期,B 值越大,那么周期越短,B 值越小,周期越長。C 值會影響圖像左右移動,C 值為正數,圖像左移,C 值為負數,圖像右移。D 值控制上下移動。
這個公式非常有用,如果下文的代碼讓你不解,記得回來查看注解。
簡單得回顧一下之后,確保你還記得這些基礎知識,那么這些曾經被得滾瓜爛熟的內容,和前端代碼結合會變成什么樣?
常見的應用場景
圖像應用
最直觀的應用是使用三角函數來繪制 Wave 曲線
for?(let?x?=?0;?x???const?y?=?Math.sin(x?*?a)?*?amplitude
}
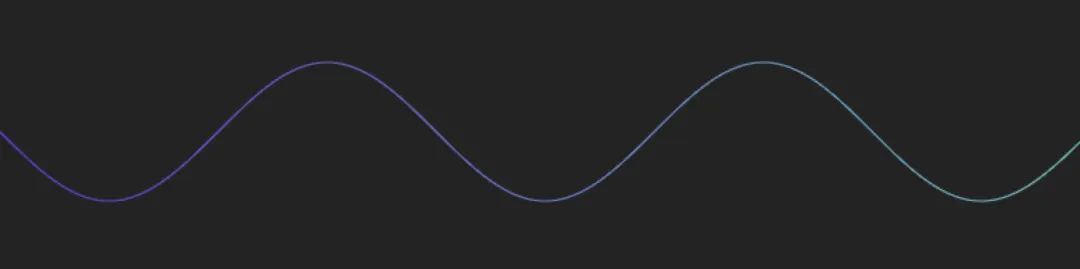
再結合三角函數偏移讓左右成為波谷,中間成為波峰,就能得到曼妙的波紋。
for?(let?x?=?0;?x???const?radians?=?x?/?width?*?Math.PI?*?2
??const?scale?=?(Math.sin(radians?-?Math.PI?*?0.5)?+?1)?*?0.5
??const?y?=?Math.sin(x?*?0.02?+?xSpeed)?*?amplitude?*?scale
}
之前掘金上很火的一篇文章,也是同樣的道理,使用兩層正弦函數繪制曲線,fill 之后加上 stagger 動畫,就能得到非常酷炫的?效果。

如果再結合鼠標位置 + lerp 動畫,就能實現堅果首頁同款的動畫。

這篇文章大部分代碼都可以在我的 Codepen 主頁看到。
SlowInSlowOut
正余弦曲線有很自然地緩入緩出的特性,并且在一個周期里面從 -1 到 1 再回到 -1,非常適合用來模擬一些物理效果。因為真實世界里面,汽車都是緩慢啟動,加速,減速,再緩慢減速直到速度變?yōu)?0 的,突變會讓人很難受。左邊的擺球是線性勻速擺動,右邊是用了三角函數優(yōu)化的結果。顯然左邊的效果設計師會打人。

只需使用 sin 或 cos 乘以最大角度,就可以得到在擺動最大角度之間的 SlowInSlowOut。
ctx.rotate(Math.cos(t?/?180?*?Math.PI)?*?Math.PI?*?0.25)
角度控制
在開發(fā)過程中,我們常常需要跟角度打交道,比如在頭像左上角(45deg)顯示 Notification 紅點,用鼠標控制 rotation 等等。
前端 JS 里面 Math.atan2(y, x) 可以用來計算 (x, y) 和 x 軸正方向的夾角弧度值。
function?getCurrentDegree?()?{
??const?deltaX?=?mouse.x?-?window.innerWidth?*?0.5
??const?deltaY?=?mouse.y?-?window.innerHeight?*?0.5
??return?Math.atan2(deltaY,?deltaX)?*?180?/?Math.PI
}

插一句,三角函數相關的動畫并不一定需要用 js 來寫,比如下面的 DEMO,使用 compass 依賴,同樣可以做到靈活控制在特定角度的動畫(千萬不要手寫各個點的坐標!!!后期沒辦法維護)
@import "compass";
.checkbox:checked {
~ button {
$per: 180 / 4;
@for $i from 1 through 6 {
&:nth-of-type(#{$i}) {
$angle: $per * ($i - 1) * 1deg + 180deg;
$x: cos($angle) * $d;
$y: sin($angle) * $d;
transform: translate($x, $y) rotate(0deg) ;
}
}
}
}

源碼(https://codepen.io/HelKyle/pen/qygvJz)
Case Study
經常用到的場景大概就這些吧,再以一個案例分析來復習一下。
前兩天在 Codepen 首頁看到熱門推薦,作者用存 css 動畫來實現一個行走的動畫,挺新穎的,然而仔細一看,腳步的動畫真心覺得別扭,于是想用三角函數優(yōu)化一下。

繪制頭部:
??drawHead?(t)?{
????ctx.save()
????ctx.beginPath()
????ctx.translate(0,?Math.sin(t)?*?4)
????ctx.arc(80,?-35,?35,?0,?2?*?Math.PI)
????ctx.fill()
????ctx.closePath()
????ctx.restore()
??}
我會給每個方法傳入周期參數 t, t 從 0 到 2 PI , 這樣能保證所有的周期運動時間同步。

身體和陰影的繪制都差不多,直接跳過看腳步動畫。
腳有兩只,按道理應該是抬腳到落腳的動作完成時,其他部位都完成了一個完整的周期,所以在繪制腳的時候,t 需要除以 2。然后第一只腳和第二只腳相差半個腳自身的周期,可以直接將 t 替換成 t + Math.PI 就是第二腳的動畫。
??drawFeet?(t)?{
??t?=?t?/?2
????ctx.translate(Math.cos(t)?*?-50,?0)
????//?另一只腳
????ctx.translate(Math.cos(t?+?Math.PI)?*?-50,?0)
??}

腳步動畫自身周期的一半是在地面上的,可以通過判斷一下 sin 值,小于 0 則不做 y 縱軸方向上的變化。
????ctx.translate(Math.cos(t)?*?-50,?Math.sin(t)?>?0???Math.sin(t)?*?-35?:?0)

還沒完,為了讓腳更加逼真,同樣在前半個周期做一下 rotate 。
????if?(t?Math.PI)?{
??????ctx.rotate(Math.sin(t)?*?Math.PI?/?180?*?-5)
????}

最終得到的效果是這樣的:
源碼(https://codepen.io/HelKyle/pen/Mqgpvb)
總結
現如今前端發(fā)展速度非常迅速,剛入門的同學剛學完 jQuery 就被告知,You Dont Need jQuery。追新的腳本根本停不下來,在學習新框架新技能的同時,也別忘了基礎知識的重要性。
好了,今天就分享到這里,希望一次匯集這么多效果,能讓你下次使用三角函數更得心應手。
以上大部分代碼都可以在我的 Codepen(https://codepen.io/HelKyle/)主頁看到。
