【算法學(xué)習(xí)】動(dòng)態(tài)規(guī)劃

動(dòng)? 態(tài)? 規(guī)? 劃

那些遺忘過(guò)去的人注定要重蹈覆轍。

——喬治·桑塔亞納（1863-1952）

今天咱們來(lái)聊聊動(dòng)態(tài)規(guī)劃。

動(dòng)態(tài)規(guī)劃(dynamic programming)是一種基礎(chǔ)的算法設(shè)計(jì)思想。作為一種尋找最優(yōu)解的通用方法，它是在20世紀(jì)50年代由美國(guó)數(shù)學(xué)家Richard Bellman（也就是之前最短路徑問(wèn)題中Bellman ford算法的發(fā)明者之一）所發(fā)明的。

動(dòng)態(tài)規(guī)劃的思想實(shí)質(zhì)是分治思想和解決冗余。

與分治法類似的是，我們將原問(wèn)題分解成若干個(gè)子問(wèn)題，先求解子問(wèn)題，再?gòu)倪@些子問(wèn)題的解得到原問(wèn)題的解。

與分治法不同的是，經(jīng)分解的子問(wèn)題往往不是互相獨(dú)立的。若用分治法來(lái)解，有些共同部分被重復(fù)計(jì)算了很多次。如果能夠保存已解決的子問(wèn)題的答案，在需要時(shí)再查找，這樣就可以避免重復(fù)計(jì)算、節(jié)省時(shí)間，也就是解決冗余。

?

實(shí)際應(yīng)用中嘗試解決一個(gè)問(wèn)題時(shí)，其實(shí)就是在思考如何將這個(gè)問(wèn)題表達(dá)成狀態(tài)（用哪些變量存儲(chǔ)哪些數(shù)據(jù)），以及如何在狀態(tài)中轉(zhuǎn)移（怎樣根據(jù)一些變量計(jì)算出另一些變量）。

?

什么是狀態(tài)？我們?cè)诮酉聛?lái)的例子中體會(huì)這個(gè)概念。

以Fibonacci數(shù)列為例，每一個(gè)Fibonacci數(shù)就是這個(gè)問(wèn)題的一個(gè)狀態(tài)，每求一個(gè)新數(shù)字只需要之前的兩個(gè)狀態(tài)。這種狀態(tài)計(jì)算很直接，只需要依照固定的模式從舊狀態(tài)計(jì)算出新狀態(tài)就行（a[i]=a[i-1]+a[i-2]），不需要考慮是不是需要更多的狀態(tài)，也不需要選擇哪些舊狀態(tài)來(lái)計(jì)算新狀態(tài)。

?

求Fibonacci數(shù)列的例子過(guò)于簡(jiǎn)單，為了解決更復(fù)雜的問(wèn)題，我們還需要引入階段的概念。

階段是指隨著問(wèn)題的解決，在同一個(gè)時(shí)刻可能會(huì)得到的不同狀態(tài)的集合。

在Fibonacci數(shù)列中，每一步會(huì)計(jì)算得到一個(gè)新數(shù)字，在這里每一步就是一個(gè)階段，而每個(gè)階段只有一個(gè)狀態(tài)（所以我們會(huì)忽略階段的概念）。

我們?cè)僖陨疃葍?yōu)先搜索走迷宮的過(guò)程為例：每一步只能走一格，因?yàn)榭梢韵蛄硗馊齻€(gè)方向走，所以每一步可能會(huì)處于很多個(gè)不同的位置。從頭開始走了幾步就是第幾個(gè)階段，每一步可能處于的位置稱為一個(gè)狀態(tài)，下一步可能到達(dá)的位置的集合就是這個(gè)階段下所有可能的狀態(tài)。

整理一下，假如問(wèn)題有n個(gè)階段，每個(gè)階段都有多個(gè)狀態(tài)，不同階段的狀態(tài)數(shù)不必相同，一個(gè)階段的一個(gè)狀態(tài)可以得到下個(gè)階段的所有狀態(tài)中的幾個(gè)。而我們要求的解一般就是最終階段的某個(gè)狀態(tài)。

?

了解了階段、狀態(tài)的概念后，我們發(fā)現(xiàn)，劃分階段、定義狀態(tài)其實(shí)就相當(dāng)于在劃分子問(wèn)題，也就是在遵循分治思想。

?

而動(dòng)態(tài)規(guī)劃有別于其他算法的關(guān)鍵在于解決冗余。

我們對(duì)問(wèn)題進(jìn)行分類，然后針對(duì)動(dòng)態(tài)規(guī)劃能解決的問(wèn)題進(jìn)行說(shuō)明，了解它是如何解決冗余的：

每個(gè)階段只有一個(gè)狀態(tài)->遞推；

每個(gè)階段的最優(yōu)狀態(tài)都是由上一個(gè)階段的最優(yōu)狀態(tài)得到的->貪心；

每個(gè)階段的最優(yōu)狀態(tài)是由之前所有階段的狀態(tài)的組合得到的->搜索；

每個(gè)階段的最優(yōu)狀態(tài)可以從之前某個(gè)階段的某個(gè)或某些狀態(tài)直接得到而不管之前這個(gè)狀態(tài)是如何得到的->動(dòng)態(tài)規(guī)劃。

在這個(gè)分類中我們也可以看出：一個(gè)問(wèn)題是該用遞推、貪心、搜索還是動(dòng)態(tài)規(guī)劃，完全是由這個(gè)問(wèn)題本身階段間狀態(tài)的轉(zhuǎn)移方式（也就是得出下一個(gè)狀態(tài)的方式）決定的。

重點(diǎn)看有關(guān)動(dòng)態(tài)規(guī)劃的部分。在這個(gè)闡述中，每個(gè)階段的最優(yōu)狀態(tài)可以從之前某個(gè)階段的某個(gè)或某些狀態(tài)直接得到（特別是與后面的階段無(wú)關(guān)），包含了兩種性質(zhì)：最優(yōu)子結(jié)構(gòu)（問(wèn)題的最優(yōu)解所包含的子問(wèn)題的解也是最優(yōu)的）和重疊子問(wèn)題（子問(wèn)題之間是不獨(dú)立的，一個(gè)子問(wèn)題在下一階段決策中可能被多次使用到）；而不管之前這個(gè)狀態(tài)是如何得到的，這個(gè)性質(zhì)叫做無(wú)后效性。

?

還是以Fibonacci數(shù)列為例。在計(jì)算到第100項(xiàng)的時(shí)候，需要用到第99項(xiàng)和98項(xiàng)（最優(yōu)子結(jié)構(gòu)，重疊子問(wèn)題）。這時(shí)候你還需要重新計(jì)算第99項(xiàng)嗎？

不需要，你只需要在第一次計(jì)算的時(shí)候把它記下來(lái)就可以了（無(wú)后效性）。

在要用到第99項(xiàng)時(shí)，如果沒有計(jì)算過(guò)，就按照遞推式計(jì)算；如果計(jì)算過(guò)，直接使用，就像把第99項(xiàng)存儲(chǔ)在一個(gè)緩存區(qū)里一樣，這種方法，叫做“記憶化”，是遞推式求解的技巧。這種技巧，通俗的說(shuō)叫“花費(fèi)空間來(lái)節(jié)省時(shí)間”：動(dòng)態(tài)規(guī)劃就是通過(guò)這樣的方式“記憶”過(guò)去，節(jié)省每次重新計(jì)算的時(shí)間。

?

我們可以用一個(gè)表來(lái)記錄所有已解的子問(wèn)題的答案。不管該子問(wèn)題以后是否被用到，只要它被計(jì)算過(guò)，就將其結(jié)果填入表中。這是動(dòng)態(tài)規(guī)劃法的基本思路。具體的動(dòng)態(tài)規(guī)劃算法多種多樣，但它們具有相同的填表格式。

我們將這個(gè)表稱為最優(yōu)決策表。最優(yōu)決策表是一個(gè)二維表，其中行表示決策的階段，列表示問(wèn)題狀態(tài)，表格需要填寫的數(shù)據(jù)一般對(duì)應(yīng)此問(wèn)題的在某個(gè)階段某個(gè)狀態(tài)下的最優(yōu)值（如最短路徑，最長(zhǎng)公共子序列，最大價(jià)值等），填表的過(guò)程就是根據(jù)遞推關(guān)系依次填寫，最后根據(jù)整個(gè)表格的數(shù)據(jù)通過(guò)簡(jiǎn)單的取舍或者運(yùn)算求得問(wèn)題的最優(yōu)解。

再以最長(zhǎng)遞增子序列問(wèn)題為例。

對(duì)于長(zhǎng)度為N的數(shù)組A[n] = {a[0], a[1], a[2], ..., a[n-1]}，將以a[j]結(jié)尾的最大遞增子序列長(zhǎng)度設(shè)為L(zhǎng)[j]，那么狀態(tài)轉(zhuǎn)移方程為：

L[j] = max(L[i]) + 1）, ??0<=i

我們對(duì)每一個(gè)A[n]中的元素都計(jì)算以他們各自結(jié)尾的最大遞增子序列的長(zhǎng)度，想求a[j]結(jié)尾的最大遞增子序列的長(zhǎng)度時(shí)，我們就需要遍歷j之前的所有位置i，找出a[i] < a[j]，計(jì)算這些i中，能產(chǎn)生最大L[i]的i，之后就可以求出L[j]。我們要求的問(wèn)題——數(shù)組A的最大遞增子序列的長(zhǎng)度，就是L[n-1]。

在這個(gè)問(wèn)題中，計(jì)算每一個(gè)L[i]的過(guò)程就是一個(gè)階段，對(duì)每一個(gè)以a[i]為結(jié)尾的子序列的長(zhǎng)度就是該階段的一個(gè)狀態(tài)。我們只需要求出每個(gè)階段的一個(gè)最優(yōu)狀態(tài)，計(jì)入表格，就可以一步步得出最終狀態(tài)，而不需要每次都循環(huán)尋找一個(gè)遞增子序列。

?

所以，尋找符合“最優(yōu)子結(jié)構(gòu)”的狀態(tài)和狀態(tài)轉(zhuǎn)移方程的定義就是我們?cè)诶脛?dòng)態(tài)規(guī)劃解決問(wèn)題時(shí)要做的。在找到之后，這個(gè)問(wèn)題就可以以“記憶化地求解遞推式”的方法來(lái)解決。而尋找到的定義，才是動(dòng)態(tài)規(guī)劃的本質(zhì)。

?

需要注意的是，一個(gè)問(wèn)題可能有多種不同的狀態(tài)定義和狀態(tài)轉(zhuǎn)移方程定義，即使存在一個(gè)有后效性的定義，也不代表該問(wèn)題一定不適用于動(dòng)態(tài)規(guī)劃。

?

總結(jié)一下解決問(wèn)題的具體步驟：

??? (1)劃分階段：按照問(wèn)題的時(shí)間或空間特征，把問(wèn)題分為若干個(gè)階段。在劃分階段時(shí)，注意劃分后的階段一定要是有序的或者是可排序的，否則問(wèn)題就無(wú)法求解。

??? (2)確定狀態(tài)和狀態(tài)變量：將問(wèn)題發(fā)展到各個(gè)階段時(shí)所處于的各種客觀情況用不同的狀態(tài)表示出來(lái)。當(dāng)然，狀態(tài)的選擇要滿足無(wú)后效性。

??? (3)確定決策并寫出狀態(tài)轉(zhuǎn)移方程：因?yàn)闆Q策和狀態(tài)轉(zhuǎn)移有著天然的聯(lián)系，狀態(tài)轉(zhuǎn)移就是根據(jù)上一階段的狀態(tài)和決策來(lái)導(dǎo)出本階段的狀態(tài)。所以如果確定了決策，狀態(tài)轉(zhuǎn)移方程也就可寫出。

??? (4)尋找邊界條件：給出的狀態(tài)轉(zhuǎn)移方程是一個(gè)遞推式，需要一個(gè)遞推的終止條件或邊界條件。

我們?cè)儆脛?dòng)態(tài)規(guī)劃的方法具體解決一個(gè)問(wèn)題：背包問(wèn)題。

一

0-1背包

有n件物品和容量為m的背包。給出每件物品的重量以及價(jià)值，求解：讓裝入背包的物品重量不超過(guò)背包容量的最大價(jià)值。

這個(gè)問(wèn)題的特點(diǎn)是每個(gè)物品只有一件供你選擇放還是不放，也就是只能在0和1之間選擇。

設(shè)dp[i][j]表示前i件物品，總重量不超過(guò)j的最大價(jià)值,W[i]表示第i件物品的重量，V[i]表示第i件物品的價(jià)值。可得出狀態(tài)轉(zhuǎn)移方程：

dp[i][j]=max{dp[i-1][j–w[i]]+v [i],dp[i-1][j] }；

?

然后就到了coding time！

//動(dòng)態(tài)規(guī)劃：01背包問(wèn)題
#include using namespace std;
int main(){  //輸入，N為物品總數(shù)量，M為背包容量，v[]表價(jià)值，w[]表重量  cout<<"輸入物品的數(shù)量和背包的最大容量："<<endl;  int N,M;  cin>>N>>M;  cout<<"輸入物品的重量、價(jià)值："<<endl;   int v[105],w[105];  for (int i=1;i<=N;i++)      cin>> w[i]>>v[i];  //初始化最優(yōu)決策表   int dp[105][105];  for (int j=0;j<=M;j++)      dp[0][j]=0;  //利用dp方程填表   for (int i=1;i<=N;i++)      for (int j=0;j<=M;j++)    {            if(w[i]<=j) dp[i][j]= (dp[i-1] [j-w[i]]+v[i])>dp[i-1][j]? (dp[i-1] [j-w[i]]+v[i]):dp[i-1][j];            else dp[i][j]=dp[i-1][j];    }  //輸出   cout<<"最大價(jià)值為"<<dp[N][M];  return 0;}

?

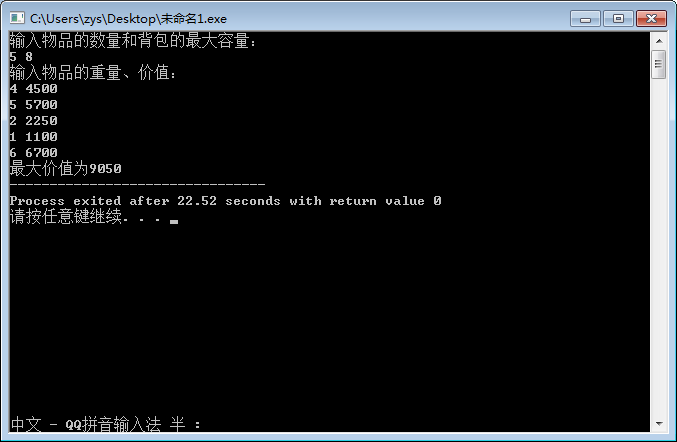
二

完全背包

有n種物品，每種物品無(wú)限個(gè)，和容量為m的背包。給出每件物品的重量以及價(jià)值，求解：讓裝入背包的物品重量不超過(guò)背包容量的最大價(jià)值。

特點(diǎn)是每個(gè)物品可以無(wú)限選用。我們將選擇的數(shù)量計(jì)為k。

?

還是依照之前的定義，直接給出狀態(tài)轉(zhuǎn)移方程：

dp[i][j] = max{ dp[i-1][ j - w[i] * k] + v[i] * k};?

（0 <= k * w[i] <= j）

?

code

//動(dòng)態(tài)規(guī)劃：完全背包問(wèn)題
#include using namespace std;
int main(){  //輸入，N為物品總數(shù)量，M為背包容量，v[]表價(jià)值，w[]表重量  cout<<"輸入物品的數(shù)量和背包的最大容量："<<endl;  int N,M;  cin>>N>>M;  cout<<"輸入物品的重量、價(jià)值："<<endl;   int v[105],w[105];  for (int i=1;i<=N;i++)      cin>> w[i]>>v[i];  //初始化最優(yōu)決策表       int dp[105][105];  for (int j=0;j<=M;j++)      dp[0][j]=0;  //利用dp方程填表      for (int i=1;i<=N;i++)      for (int j=0;j<=M;j++){         for (int k = 0; k * w[i] <= j; k++){          dp[i][j]= (dp[i-1] [j-w[i]*k]+v[i]*k)>dp[i-1][j]? (dp[i-1] [j-w[i]*k]+v[i]*k):dp[i-1][j];        }      }  //輸出   cout<<"最大價(jià)值為"<<dp[N][M];  return 0;}

?

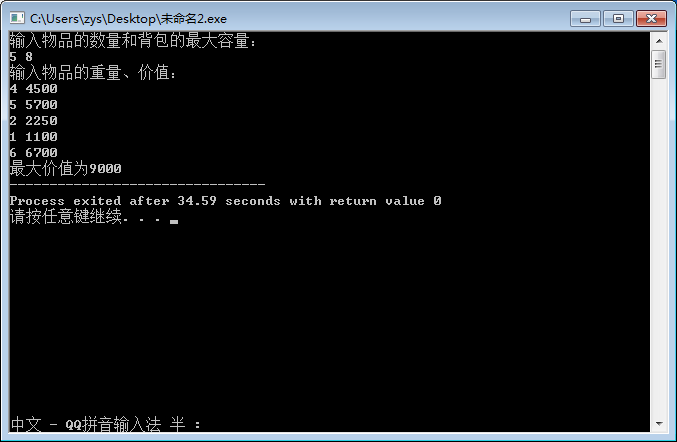
三

多重背包

有n件物品和容量為m的背包。給出每件物品的重量，價(jià)值，數(shù)量。求解：讓裝入背包的物品重量不超過(guò)背包容量的最大價(jià)值。

特點(diǎn)是每個(gè)物品都有了一定的數(shù)量限制。

?

狀態(tài)轉(zhuǎn)移方程：

dp[i][j] = max{ dp[i-1][ j - w[i] * k ] + v[i] * k };?

（0 <= k * w[i] <= j，0<=k<=n[i]）

?

code

//動(dòng)態(tài)規(guī)劃：多重背包問(wèn)題
#include using namespace std;
int main(){  //輸入，N為物品總數(shù)量，M為背包容量，v[]表價(jià)值，w[]表重量，n[]表數(shù)量   cout<<"輸入物品的數(shù)量和背包的最大容量："<<endl;  int N,M;  cin>>N>>M;  cout<<"輸入物品的重量、價(jià)值、數(shù)量："<<endl;   int v[105],w[105],n[105];  for (int i=1;i<=N;i++)      cin>> w[i]>>v[i]>>n[i];  //初始化最優(yōu)決策表   int dp[105][105];  for (int j=0;j<=M;j++)      dp[0][j]=0;  //利用dp方程填表   for (int i=1;i<=N;i++)      for (int j=0;j<=M;j++){         for (int k = 0;k * w[i] <= j && k<=n[i]; k++){          dp[i][j]= (dp[i-1] [j-w[i]*k]+v[i]*k)>dp[i-1][j]? (dp[i-1] [j-w[i]*k]+v[i]*k):dp[i-1][j];        }      }  //輸出   cout<<"最大價(jià)值為"<<dp[N][M];  return 0;}

?

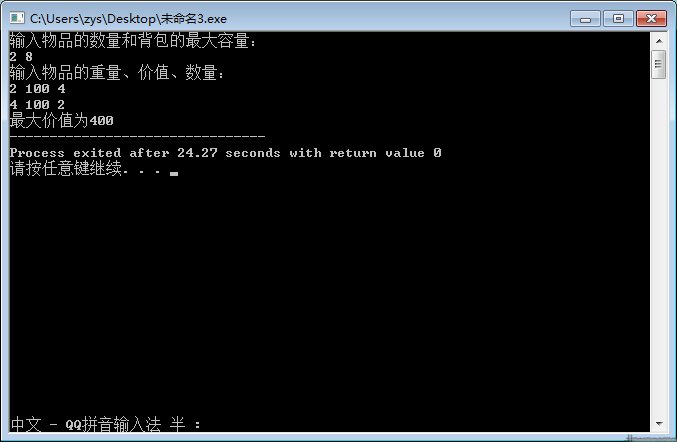
關(guān)于背包問(wèn)題可以有很多拓展，這里只是簡(jiǎn)單地暴力地運(yùn)用dp方程實(shí)現(xiàn)了問(wèn)題而已，還有很大的優(yōu)化提升空間。具體拓展可以看看dd_engi大牛的背包九講，很詳細(xì)。

那么，本期就到此為止了。蟹蟹大家的閱讀。

#

-The End-

文/今天不太想說(shuō)話的新手舟

版/真的要考試了的小白舟

碼/這期減少了題目量的工人舟

審/老板短短的路走走停停

#