夜夜嗨色刺激,操骚逼屄视频,69欧美在线,欧美夜夜操,小h片在线观看,日本一区视频免费,9999久久久久,综合色图91

算法的重要性，我就不多說了吧，想去大廠，就必須要經過基礎知識和業(yè)務邏輯面試+算法面試。所以，為了提高大家的算法能力，這個公眾號后續(xù)每天帶大家做一道算法題，題目就從LeetCode上面選！

今天和大家聊的問題叫做?不同路徑，我們先來看題面：

https://leetcode-cn.com/problems/unique-paths/

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

題意

一個機器人位于一個 m x n 網格的左上角（起始點在下圖中標記為“Start” ）。

機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為“Finish”）。

問總共有多少條不同的路徑？

樣例

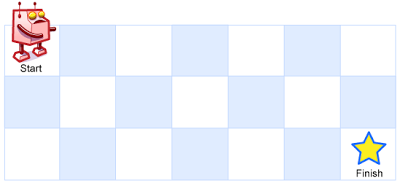
示例?1:

輸入: m = 3, n = 2
輸出: 3
解釋:
從左上角開始，總共有 3 條路徑可以到達右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例?2:

輸入: m = 7, n = 3
輸出: 28

解題

https://www.cnblogs.com/techflow/p/12872847.html

解法

在我寫題解的時候，我突然想起來上一次見到它好像是在某個綜藝節(jié)目當中。它被作為一道智力題來考一些明星嘉賓，好像一眾明星里面，只有關曉彤做了出來。。。

它作為智力題有一個標準的模板式解法：

對于圖中的C點來說，從起點通往它的路徑數(shù)量等于通往A點和B點路徑的和。

這個結論我們很多人都知道，因為C點只有兩個來源，一個是A點一個是B點。它既可以從A點來，也可以從B點來，所以應該是一個加和的關系。

這當然是沒錯的，但不知道大家從這個過程當中有沒有什么感悟。C點的上游是A點和B點，也就是說C狀態(tài)是由A狀態(tài)或者是B狀態(tài)轉移到的。這不就是一個動態(tài)規(guī)劃算法嗎？

我們用dp記錄每一個位置的答案的話，那么可以很輕松地寫出狀態(tài)轉移方程：

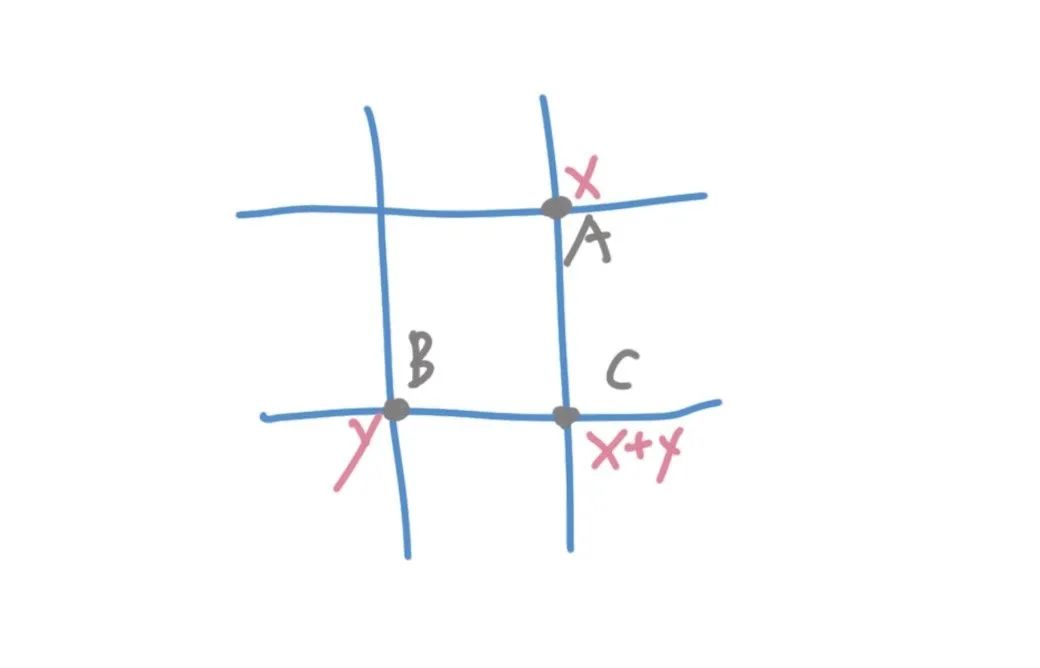
dp[i][j] = dp[i-1][j] + dp[i][j-1]

我們用代碼把這個方程實現(xiàn)就能解出問題了。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = [[0 for _ in range(n+2)] for _ in range(m+2)]
        
        dp[0][1] = 1
        
        for i in range(1, m+1):
            # 特殊處理第一列，因為第一列只有1種
            dp[i][1] = dp[i-1][1]
            for j in range(2, n+1):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
                
        return dp[m][n]

one more solution

如果只有上面這一種解法，那么這道題完全沒有說的必要，也太簡單了。這道題還有另外一種解法，會更加簡單。

在上面的解法當中，我們是把這個問題當成了算法題來解決的，使用動態(tài)規(guī)劃算法進行建模，適配題目來解決它。但如果我們換個思路，完全可以把它當做數(shù)學問題來解。

我們來分析一下問題，機器人要從左上角走到右下角，地圖是沒有缺陷的，所有點都可以到達。由于機器人沒辦法走回頭路，也就是說機器人在通往終點的過程當中走過的路程是確定的。也就是要走n-1條橫邊和m-1條豎邊。

邊的總數(shù)和種類都確定了，其實這個問題可以轉化一下。我們把走的橫邊看成是白球，走的豎邊看成是黑球，那么這道題其實就可以轉化成，我們有n-1個白球，m-1個黑球，現(xiàn)在把它們排成一排，一共有多少種方法？

這個是小學的組合數(shù)學問題，我們要從整體的n+m-2個物體當中，選出n-1個，那么顯然答案就是：

不過，雖然我們用一個式子就表達了，但是要求解這個組合數(shù)，還是需要通過循環(huán)的。我們把它轉化成:

接著我們用循環(huán)求解即可。

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        ret = 1
        
        for i in range(1, n):
            ret = ret * (n+m-1-i) // i
        return ret

相比于上面的做法更加簡短，雖然兩者看起來都是

的算法，好像差別不大。但是每個數(shù)的階乘和組合數(shù)都是可以預處理的，在頻繁求解的場景下，顯然要比動態(tài)規(guī)劃算法更快。

好了，今天的文章就到這里，如果覺得有所收獲，請順手點個在看或者轉發(fā)吧，你們的支持是我最大的動力。

上期推文：

LeetCode1-50題匯總，速度收藏！

LeetCode40-60題匯總，速度收藏！

LeetCode刷題實戰(zhàn)61：旋轉鏈表

?LeetCode刷題實戰(zhàn)62：不同路徑

題意

解題

解法

one more solution