人人透人人摸,国产精品一线在线观看,国产精品久久久精品,亚洲经典免费视频,小泽玛莉亚黑人初体验,久久99精品波多野结衣一区,日韩激情小说,天堂AV在线资源

點擊上方“小白學(xué)視覺”，選擇加"星標"或“置頂”

重磅干貨，第一時間送達

編者按

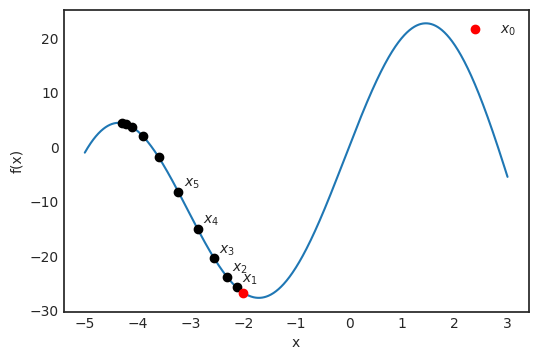
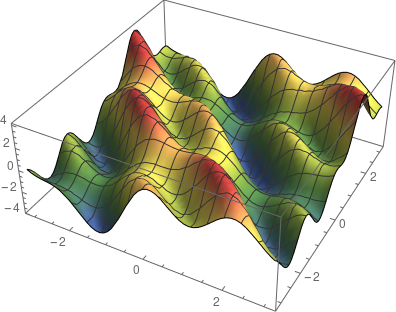
什么是優(yōu)化呢？優(yōu)化就是尋找函數(shù)的極值點。既然是針對函數(shù)的，其背后最重要的數(shù)學(xué)基礎(chǔ)是什么呢？沒錯，就是微積分。那什么是微積分呢？微積分就是一門利用極限研究函數(shù)的科學(xué)。本文從一維函數(shù)的優(yōu)化講起，拓展到多維函數(shù)的優(yōu)化，詳細闡述了優(yōu)化背后的數(shù)學(xué)基礎(chǔ)。

深度學(xué)習(xí)中的優(yōu)化是一項極度復(fù)雜的任務(wù)，本文是一份基礎(chǔ)指南，旨在從數(shù)學(xué)的角度深入解讀優(yōu)化器。

一般而言，神經(jīng)網(wǎng)絡(luò)的整體性能取決于幾個因素。通常最受關(guān)注的是網(wǎng)絡(luò)架構(gòu)，但這只是眾多重要元素之一。還有一個常常被忽略的元素，就是用來擬合模型的優(yōu)化器。

為了說明優(yōu)化的復(fù)雜性，此處以 ResNet 為例。ResNet18 有 11,689,512 個參數(shù)。尋找最佳參數(shù)配置，也就是在 11,689,512 維的空間中定位一個點。如果暴力搜索的話，可以把這個空間分割成網(wǎng)格。假設(shè)將每個維度分成十格，那么就要檢查 10^11689512（10 的 11689512 次方）組可能的配置，對每一組配置都要計算損失函數(shù)，并找出損失最小的配置。

10 的 11689512 次方是一個什么概念？已知宇宙中的原子才只有 10^83 個，宇宙的年齡只有 4.32 x 10^17 秒（約 137 億年）。如果從大爆炸開始，每秒檢查 10^83 個原子，我們現(xiàn)在才檢查了 4.32*10^1411 個，遠遠小于上述網(wǎng)格可能的配置數(shù)。

所以優(yōu)化器非常重要。它們就是用來處理這種難以理解的復(fù)雜性的。有了它，你就可以將訓(xùn)練網(wǎng)絡(luò)的時間壓縮在幾天內(nèi)，而不是數(shù)十億年間。下文將從數(shù)學(xué)角度深入研究優(yōu)化器，并了解它們是如何完成這一看似不可能的任務(wù)的。

優(yōu)化的基礎(chǔ)

我們從簡單的地方開始。假設(shè)要最大化單變量函數(shù)。（在機器學(xué)習(xí)中，通常以最小化損失函數(shù)為目標，不過最小化就等同于最大化函數(shù)的負值。）

定義：

對函數(shù)作圖：

最直觀的方法是將這條線劃分成網(wǎng)格，檢查每個點的值，然后選擇函數(shù)值最大的點。正如引言中所說，這是不可擴展的，因此要找其他解決方案。將這條線想象成一座要爬到頂峰的山。假設(shè)位于紅點處：

如果要到達山峰，該往哪個方向走？當然，應(yīng)該向斜率增加的地方前進。這個概念對應(yīng)的是函數(shù)的導(dǎo)數(shù)。在數(shù)學(xué)上，導(dǎo)數(shù)定義為：

乍看之下，導(dǎo)數(shù)非常神秘，但它的幾何意義非常簡單。仔細看一下求導(dǎo)的點：

對任何 x 和 y，通過 f(x) 和 f(y) 的這條線定義為：

一般而言，如果用 at+b 定義一條直線，那稱 a 為這條線的斜率。這個值既可以是正值也可以是負值，斜率為正，直線向上走；斜率為負，直線向下走。絕對值越大，直線越陡。如果像導(dǎo)數(shù)定義中一樣，讓 y 越來越接近 x，那么這條線就會成為 x 處的切線。

（圖注）在 x=-2.0 時，f(x)的切線和逼近線。

切線為：

切線方向記為向量(1,f’(x))。

如果從 x_0=-2.0 的位置開始登山，應(yīng)該沿切線上升的方向前進。如果切線的斜率較大，可以大步邁進；如果斜率接近零，應(yīng)該小步小步往上爬，以免越過峰值。如果用數(shù)學(xué)語言表示，我們應(yīng)該用下面這種方式定義下一個點：

式中 λ 是個參數(shù)，設(shè)置前進的步長。這就是所謂的學(xué)習(xí)率。通常，后續(xù)步驟定義為：

正導(dǎo)數(shù)意味著斜率在增加，所以可以前進；而負導(dǎo)數(shù)意味著斜率在減少，所以要后退。可視化這個過程：

如你所見，這個簡單的算法成功地找到了峰值。但如圖所示，這并非函數(shù)的全局最大值。在所有的優(yōu)化算法中，這都是一個潛在的問題，但還是有解決辦法的。

在這個簡單的例子中，我們只最大化了單變量函數(shù)。這樣雖然可以有效地說明這個概念，但在現(xiàn)實生活中，可能存在數(shù)百萬變量，神經(jīng)網(wǎng)絡(luò)中就是如此。下一部分將會介紹，如何將這樣簡單的算法泛化到多維函數(shù)的優(yōu)化。

多維優(yōu)化

在單變量函數(shù)中，可以將導(dǎo)數(shù)視為切線的斜率。但遇到多個變量，則不能如此。先來看個具體的例子。定義函數(shù)：

這個函數(shù)將是這部分的 toy example 。

對 f(x,y)作圖。

這是一個有兩個變量的函數(shù)，圖像是一個曲面。馬上可以發(fā)現(xiàn)，這樣很難定義切線的概念，因為與曲面上一個點相切的線有很多。事實上，可以做一個完整的平面。這就是切平面。

f(x,y)在點 (0,0) 處的切平面。

但切平面有兩個非常特別的方向。以點 (0,0) 處的切平面為例。對每一個多變量函數(shù)來說，先固定所有變量只取一個能動的變量，這樣這個函數(shù)基本上就變成單變量函數(shù)了。示例函數(shù)變?yōu)椋?/span>

和：

可以用垂直于坐標軸的平面分割曲面，來可視化上面這兩個函數(shù)。平面和曲面相交處就是 f(x,0) 或 f(0,y)，這取決于你用哪個平面。

用垂直的平面切割曲面，可視化 f(0,x)。

對這些函數(shù)，就可以像上文一樣定義導(dǎo)數(shù)了。這就是所謂的偏導(dǎo)數(shù)。要泛化之前發(fā)現(xiàn)峰值的算法，偏導(dǎo)數(shù)起著至關(guān)重要的作用。用數(shù)學(xué)語言定義：

每個偏導(dǎo)數(shù)表示切平面上的一個方向。

切平面上偏導(dǎo)數(shù)的方向。

偏導(dǎo)數(shù)的值是特殊切線的斜率。最陡的方向根據(jù)梯度確定，定義為：

注意，梯度是參數(shù)空間中的方向。可以輕松在二維平面中繪制出梯度，如下圖所示：

f(x,y)的梯度。

綜上所述，發(fā)現(xiàn)峰值的算法現(xiàn)在成為：

這就是所謂的梯度上升（gradient ascent）。如果要求函數(shù)最小值，就要沿負梯度的方向邁出一步，也就是下降最陡的方向：

這就是所謂的梯度下降（gradient descent），你可能會很頻繁地看到它，因為在機器學(xué)習(xí)中，實際上是要最小化損失。

為什么梯度指向最陡的上升方向？

在這種情況下，要知道為什么梯度給出的是最陡峭的上升方向。為了給出精確的解釋，還要做一些數(shù)學(xué)計算。除了用垂直于 x 軸或 y 軸的垂直平面切割曲面外，還可以用 (a,b) 任意方向的垂直平面切割曲面。對于偏導(dǎo)數(shù)，有：

可以將它們視為 f(x,y) 沿 (1,0) 和(0,1)方向的導(dǎo)數(shù)。盡管這些方向特別重要，但也可以任意規(guī)定這些方向。也就是說，假設(shè)方向為：

這個方向的導(dǎo)數(shù)定義為：

注意，最后一個等式就是方向向量和梯度的點積，這可能和高中幾何課堂上遇到的點積是相同的。所以：

問題是，哪個方向的方向?qū)?shù)最大？答案是上升程度最陡峭的方向，所以如果要優(yōu)化，得先知道這個特定的方向。這個方向就是之前提過的梯度，點積可以寫作：

式中的 |.| 表示向量長度，α是兩向量間的夾角（這在任意維數(shù)上都是成立的，不只是二維）。顯而易見，當 cosα=1，即 α=0 時，表達式取最大值。這就意味著這兩個向量是平行的，所以 e 的方向和梯度方向是相同的。

訓(xùn)練神經(jīng)網(wǎng)絡(luò)

現(xiàn)在要從理論轉(zhuǎn)戰(zhàn)實踐了，了解如何訓(xùn)練神經(jīng)網(wǎng)絡(luò)。假設(shè)任務(wù)是將有 n 維特征向量的圖像分成 c 類。從數(shù)學(xué)角度看，神經(jīng)網(wǎng)絡(luò)代表將 n 維特征空間映射到 c 維空間的函數(shù) f：

神經(jīng)網(wǎng)絡(luò)本身是參數(shù)化的函數(shù)。方便起見，將參數(shù)標記為 m 維向量：

為了表現(xiàn)出對參數(shù)的依賴，習(xí)慣記為：

將神經(jīng)網(wǎng)絡(luò)的參數(shù)空間映射為實數(shù)。損失函數(shù)記為：

式中的

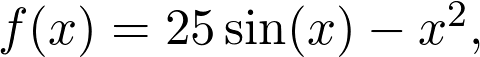
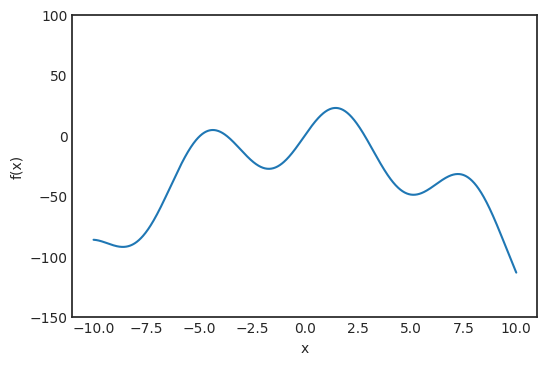
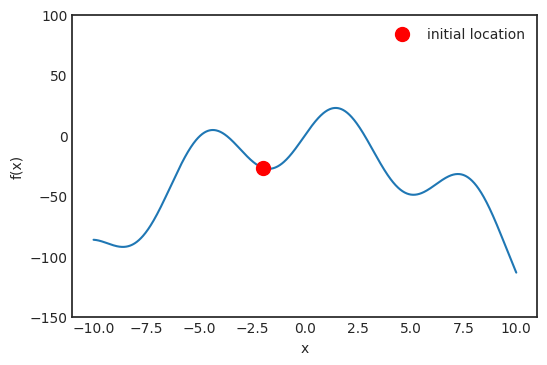
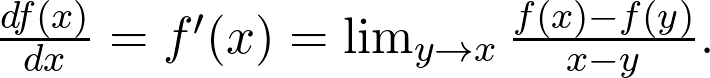
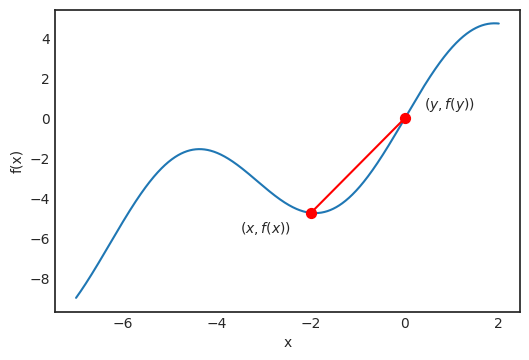
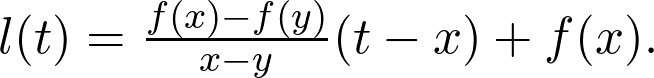
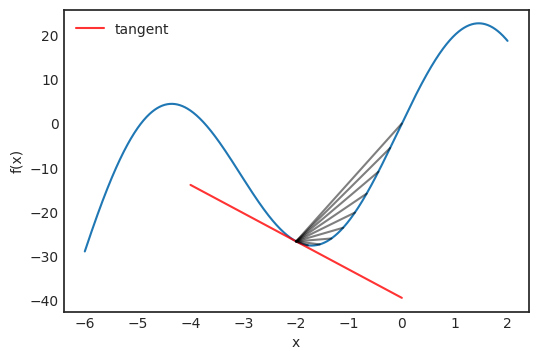
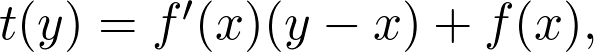
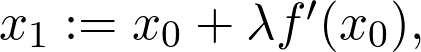
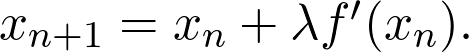
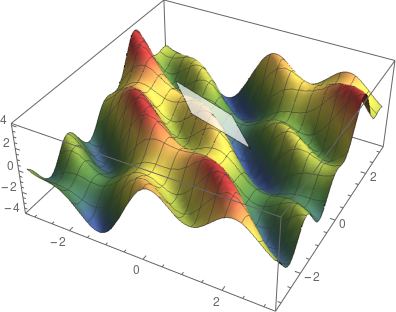
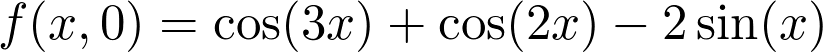
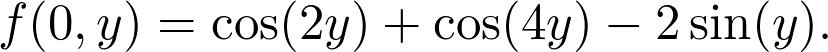
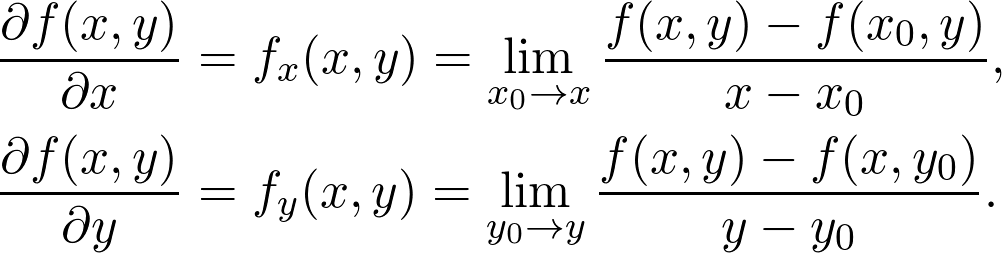
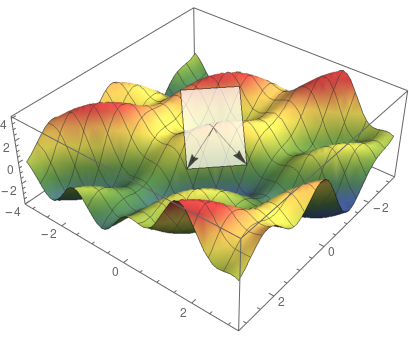
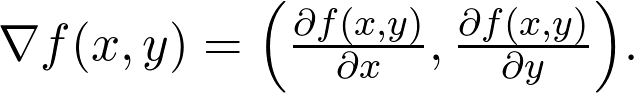
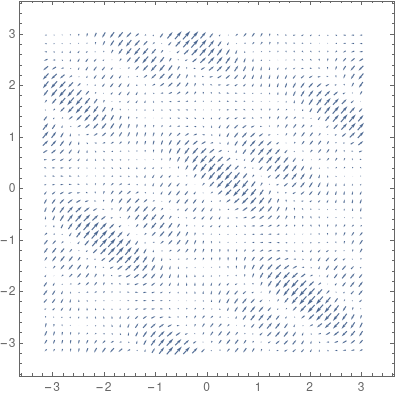
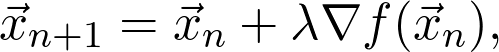
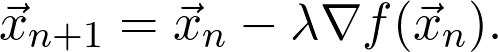
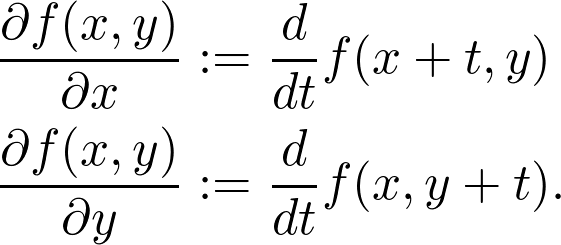
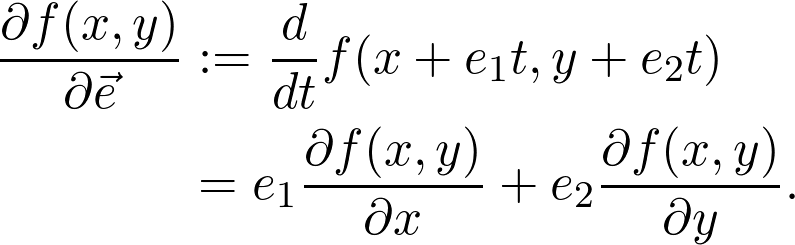
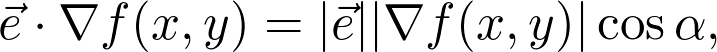
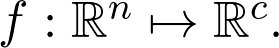
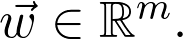
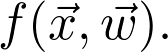
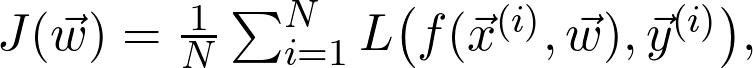
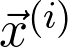是觀測值為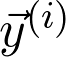

的第 i 個數(shù)據(jù)點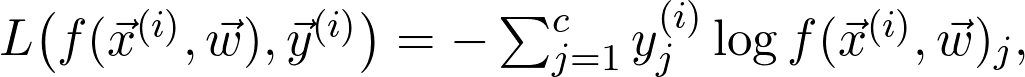

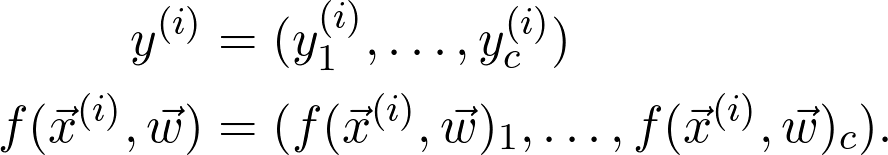
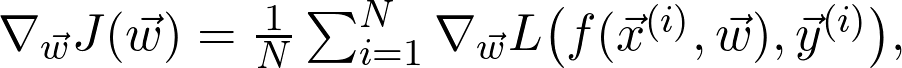
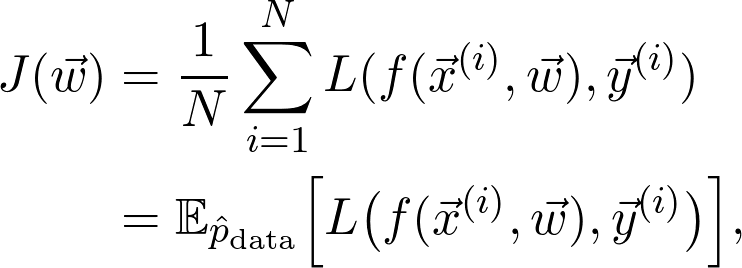
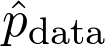L 是損失函數(shù)項。例如，如果 J 是交叉熵損失，則：

式中

這看似簡單，但難以計算。在真實世界中有數(shù)百萬個數(shù)據(jù)點 N，更別說參數(shù) m 的數(shù)量了。所以，一共有數(shù)百萬項，因此要計算數(shù)百萬個導(dǎo)數(shù)來求最小值。那么在實踐中該如何解決這一問題？

隨機梯度下降

要用梯度下降，得先計算：

如果 N 很大，那么計算量就很大，而一般都希望 N 大一點（因為想要盡量多的數(shù)據(jù)）。可以化簡嗎？一種方式是忽略一部分。盡管這看起來像個不靠譜的方案，但卻有堅實的理論基礎(chǔ)。要理解這一點，首先注意 J 其實可以寫成期望值：

式中的

是訓(xùn)練數(shù)據(jù)給出的（經(jīng)驗）概率分布。可以將序列寫成：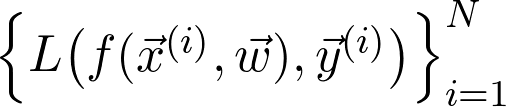

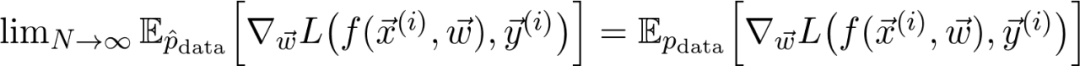
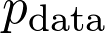這樣就成了獨立同分布的隨機變量。根據(jù)大數(shù)定律：

式中

是真正的總體分布（這是未知的）。再詳細點說，因為增加了訓(xùn)練數(shù)據(jù)，損失函數(shù)收斂到真實損失。因此，如果對數(shù)據(jù)二次采樣，并計算梯度：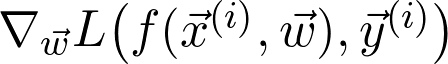

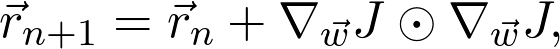
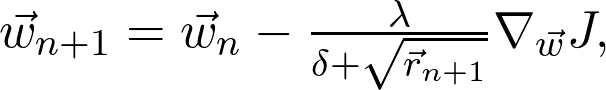
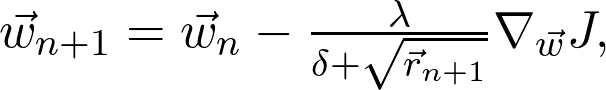
對某些 i，如果計算足夠，仍然可以得到合理的估計。這就是所謂的隨機梯度下降，記為 SGD （Stochastic Gradient Descent）。

我認為，研究人員和數(shù)據(jù)科學(xué)家能有效訓(xùn)練深度神經(jīng)網(wǎng)絡(luò)依賴于三個基礎(chǔ)發(fā)展：將 GPU 作為通用的計算工具、反向傳播還有隨機梯度下降。可以肯定地說，如果沒有 SGD，就無法廣泛應(yīng)用深度學(xué)習(xí)。

與幾乎所有新方法一樣，SGD 也引入了一堆新問題。最明顯的是，二次采樣的樣本量要有多大？太小可能會造成梯度估計有噪聲，太大則會造成收益遞減。選擇子樣本也需要謹慎。例如如果所有子樣本都屬于一類，估計值可能會相差甚遠。但在實踐中，這些問題都可以通過實驗和適當隨機化數(shù)據(jù)來解決。

改善梯度下降

梯度下降（以及 SGD 變體）存在一些問題，因此這些方法在某些情況下可能會無效。例如，學(xué)習(xí)率控制著梯度方向上前進的步長。在這個參數(shù)上一般會犯兩個錯誤。第一，步長太大，以至于損失無法收斂，甚至可能分散；第二，步長太小，可能因為前進太慢，永遠都無法到達局部最小值。為了闡明這個問題，以 f(x)=x+sin x 函數(shù)為例進行研究：

假設(shè)從 x_0=2.5 開始進行梯度下降，學(xué)習(xí)率 α 分別為 1、0.1 和 0.01。

理解起來可能不夠直觀，所以對每個學(xué)習(xí)率的 x-s 繪圖：

當 α=1 時，圖像在兩點間震蕩，無法收斂到局部最小值；當 α=0.01 時，收斂得似乎很慢。在本例中，α=0.1 似乎是合適的。那在一般情況下該如何確定這個值呢？這里的中心思想是，學(xué)習(xí)率不一定是恒定的。同理，如果梯度幅度很大，就應(yīng)該降低學(xué)習(xí)率，避免跳得太遠。另一方面，如果梯度幅度較小，那可能意味著接近局部最優(yōu)值了，所以要避免超調(diào)（overshooting）的話，學(xué)習(xí)率絕對不能再增加了。動態(tài)改變學(xué)習(xí)率的算法也就是所謂的自適應(yīng)算法。

最流行的自適應(yīng)算法之一是 AdaGrad。它會累積存儲梯度幅度和大小，并根據(jù)記錄調(diào)整學(xué)習(xí)率。AdaGrad 定義了累積變量 r_0=0 并根據(jù)規(guī)則進行更新：

式中的

表示兩個向量的分量乘積。將其用于度量學(xué)習(xí)率：

式中的 δ 是為了保持數(shù)據(jù)穩(wěn)定的數(shù)值，平方根是根據(jù)分量取的。首先，當梯度大時，累積變量會很快地增長，學(xué)習(xí)率會下降。當參數(shù)接近局部最小值時，梯度會變小，學(xué)習(xí)率會停止下降。

當然，AdaGrad 是一種可能的解決方案。每一年都會有越來越多先進的優(yōu)化算法，來解決梯度下降相關(guān)的問題。但即便是最先進的方法，使用并調(diào)整學(xué)習(xí)率，都是很有好處的。

另一個關(guān)于梯度下降的問題是要確定全局最優(yōu)值或與之接近的局部最優(yōu)值。看前面的例子，梯度下降通常會陷入局部最優(yōu)值。為了更好地了解這一問題和更好的解決辦法，建議您閱讀 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 所著的《深度學(xué)習(xí)》（Deep Learning）第八章（https://www.deeplearningbook.org/）。

深度神經(jīng)網(wǎng)絡(luò)的損失函數(shù)什么樣？

前面的例子只可視化了非常簡單的玩具示例，比如 f(x)=25sin x-x^2。這是有原因的：繪制超過兩個變量的函數(shù)圖像很難。考慮到固有的局限性，我們最多只能在三個維度上進行觀察和思考。但為了了解神經(jīng)網(wǎng)絡(luò)中的損失函數(shù)，可以采取一些技巧。Hao Li 等人發(fā)表的論文《Visualizing the Loss Landscape of Neural Nets》（https://arxiv.org/pdf/1712.09913.pdf）就是有關(guān)這個的，他們選擇兩個隨機方向，對二變量函數(shù)繪圖，從而可視化損失函數(shù)。

（為了避免因尺度不變而引起的失真，他們還在隨機方向中引入了一些歸一化因素。）他們的研究揭示了在 ResNet 架構(gòu)中，殘差連接是如何影響損失，讓優(yōu)化變得更容易的。

圖像來源：Hao Li 等人所著《Visualizing the Loss Landscape of Neural Nets》（https://arxiv.org/pdf/1712.09913.pdf）。

無論殘差連接做出了多顯著的改善，我在這里主要是想說明多維優(yōu)化的難度。在圖中的第一部分可以看出，有多個局部最小值、峰值和平穩(wěn)值等。好的架構(gòu)可以讓優(yōu)化變得更容易，但完善的優(yōu)化實踐，可以處理更復(fù)雜的損失情況。架構(gòu)和優(yōu)化器是相輔相成的。

總結(jié)

我們在前文中已經(jīng)了解了梯度背后的直觀理解，并從數(shù)學(xué)角度以精確的方式定義了梯度。可以看出，對于任何可微函數(shù)，無論變量數(shù)量如何，梯度總是指向最陡的方向。從概念上來講非常簡單，但當應(yīng)用在有數(shù)百萬變量的函數(shù)上時，存在著很大的計算困難。隨機梯度下降可以緩解這個問題，但還存在陷入局部最優(yōu)、選擇學(xué)習(xí)率等諸多問題。因此，優(yōu)化問題還是很困難的，需要研究人員和從業(yè)人員多加關(guān)注。事實上，有一個非常活躍的社區(qū)在不斷地進行改善，并取得了非常驚人的成績！

下載1：OpenCV-Contrib擴展模塊中文版教程

在「小白學(xué)視覺」公眾號后臺回復(fù)：擴展模塊中文教程，即可下載全網(wǎng)第一份OpenCV擴展模塊教程中文版，涵蓋擴展模塊安裝、SFM算法、立體視覺、目標跟蹤、生物視覺、超分辨率處理等二十多章內(nèi)容。

下載2：Python視覺實戰(zhàn)項目52講

在「小白學(xué)視覺」公眾號后臺回復(fù)：Python視覺實戰(zhàn)項目，即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計數(shù)、添加眼線、車牌識別、字符識別、情緒檢測、文本內(nèi)容提取、面部識別等31個視覺實戰(zhàn)項目，助力快速學(xué)校計算機視覺。

下載3：OpenCV實戰(zhàn)項目20講

在「小白學(xué)視覺」公眾號后臺回復(fù)：OpenCV實戰(zhàn)項目20講，即可下載含有20個基于OpenCV實現(xiàn)20個實戰(zhàn)項目，實現(xiàn)OpenCV學(xué)習(xí)進階。

交流群

歡迎加入公眾號讀者群一起和同行交流，目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學(xué)影像、GAN、算法競賽等微信群（以后會逐漸細分），請掃描下面微信號加群，備注：”昵稱+學(xué)校/公司+研究方向“，例如：”張三?+?上海交大?+?視覺SLAM“。請按照格式備注，否則不予通過。添加成功后會根據(jù)研究方向邀請進入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告，否則會請出群，謝謝理解~

AI | 優(yōu)化背后的數(shù)學(xué)基礎(chǔ)