從有理數(shù)到實數(shù)和數(shù)的連續(xù)體
日期?:?2022年02月12日?? ? ??
正文共?:10551字
無理數(shù)或?qū)崝?shù)的定義; 實數(shù)集為什么是連續(xù)的、實數(shù)集里的數(shù)為什么可以和數(shù)軸上的點一一對應; 無理數(shù)的獨特性質(zhì); 無理數(shù)為什么也滿足有理數(shù)的運算法則和運算性質(zhì)(如乘法結合律、分配律等);
第一部分 從有理數(shù)集到連續(xù)的實數(shù)集
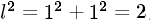 ,如果那個交點是有理點,那么l就應該是一個有理數(shù),則l可以用這種形式唯一表示,即l=q,按規(guī)定p和q沒有比1大的公因子,把l換成后有(p/q)^2=2,接下來我們將導出與此相悖的結論出來。稍作變換得到
,如果那個交點是有理點,那么l就應該是一個有理數(shù),則l可以用這種形式唯一表示,即l=q,按規(guī)定p和q沒有比1大的公因子,把l換成后有(p/q)^2=2,接下來我們將導出與此相悖的結論出來。稍作變換得到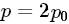 ,是整數(shù),把前面等式的p換作
,是整數(shù),把前面等式的p換作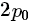 后有
后有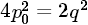 ,即
,即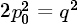 ,這說明是偶數(shù),顯然q也必須是偶數(shù),這就證明了p和q有公因子2,這與前面的"p和q沒有比1大的公因子"這個規(guī)定矛盾,而造成這種矛盾的起因就是我們一開始假設那個交點是有理點,所以數(shù)軸上的點并非都有有理數(shù)與之對應,可稱沒有有理數(shù)與之對應的點為"無理點",很容易能在數(shù)軸上構造出無數(shù)多個無理點出來。
,這說明是偶數(shù),顯然q也必須是偶數(shù),這就證明了p和q有公因子2,這與前面的"p和q沒有比1大的公因子"這個規(guī)定矛盾,而造成這種矛盾的起因就是我們一開始假設那個交點是有理點,所以數(shù)軸上的點并非都有有理數(shù)與之對應,可稱沒有有理數(shù)與之對應的點為"無理點",很容易能在數(shù)軸上構造出無數(shù)多個無理點出來。第二部分 定義實數(shù)的方式
第三部分 回顧Dedekind對實數(shù)的定義方式

Courant and Robbins, What Is Mathematics? Second Edition, P60? John Stillwell, Numbers and Geometry, P260? Richard Dedekind,?Essays on the Theory of Numbers, P5? Richard Dedekind,?Essays on the Theory of Numbers, P5? Richard Dedekind,?Essays on the Theory of Numbers, P9? Richard Courant, Fritz John, Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, P2? Terence Tao, Analysis I, third edition, P117? David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, P21? David French Belding, Kevin J. Mitchell, Foundations of Analysis, 2nd Edition, P21? Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P984? Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P986? D.C. Goldrei, Classic Set Theory: For Guided Independent Study,P8? Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P987? P. Ehrlich,Real Numbers, Generalizations of the Reals, and Theories of Continua, page x? Hans Niels Jahnke ,A History of Analysis,P306? S. C. Malik, Principles of Real Analysis,P18? Courant and Robbins, What Is Mathematics? Second Edition, P71? Rudiments of Mathematics Part 1, Academic Publishers,P15? Richard Dedekind, Essays on the Theory of Numbers, P7? Morris Kline, Mathematical Thought from Ancient to Modern Times, Vol. 3, 1990 edition, P986?
—?THE END —

評論
圖片
表情
