一個(gè)決策的做出，需要考慮一系列盤根錯(cuò)節(jié)的問題。

決策樹是一個(gè)通過特征學(xué)習(xí)決策規(guī)則，用于預(yù)測(cè)目標(biāo)的監(jiān)督機(jī)器學(xué)習(xí)模型。顧名思義，該模型通過提出一系列的問題將數(shù)據(jù)進(jìn)行分解，從而做出決策。

下圖示例中用決策樹決定某一天的活動(dòng)：

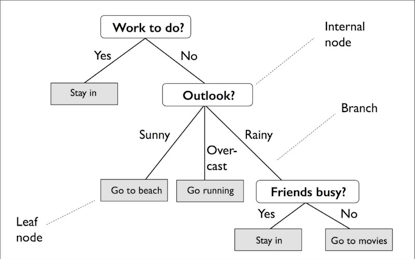
根據(jù)訓(xùn)練集的特征，決策樹模型學(xué)習(xí)一系列問題來推斷樣本的類標(biāo)簽。從圖中可以看出，如果可解讀性是重要因素，決策樹模型是個(gè)不錯(cuò)的選擇。

盡管上圖顯示了基于分類目標(biāo)（分類）的決策樹的概念，但如果目標(biāo)為實(shí)數(shù)，它也同樣使用（回歸）。

本教程將討論如何使用Python的scikit-learn庫構(gòu)建決策樹模型。其中將包括：

• 決策樹的基本概念
• 決策樹學(xué)習(xí)算法背后的計(jì)算
• 信息增益和不純性度量
• 分類樹
• 回歸樹

決策樹的基本概念

決策樹是通過遞歸拆分構(gòu)成的——先從根節(jié)點(diǎn)開始（也稱為父節(jié)點(diǎn)），將每個(gè)節(jié)點(diǎn)分為左右子節(jié)點(diǎn)。這些節(jié)點(diǎn)可以再進(jìn)一步分裂成其他子節(jié)點(diǎn)。

比如說上圖中，根節(jié)點(diǎn)為Work to do?，然后根據(jù)是否有活動(dòng)需要完成而分裂為子節(jié)點(diǎn)Stay in和Outlook。Outlook節(jié)點(diǎn)再繼續(xù)分裂為三個(gè)子節(jié)點(diǎn)。

那么，如何確定各個(gè)節(jié)點(diǎn)的最佳分裂點(diǎn)呢？

從根節(jié)點(diǎn)開始，數(shù)據(jù)在能產(chǎn)生最大信息增益 (IG) 的特征上產(chǎn)生分裂（下文將有更詳細(xì)的解釋）。在迭代過程中，該分裂過程將在每個(gè)子節(jié)點(diǎn)持續(xù)重復(fù)，直到所有的葉子達(dá)到純性為止，即每個(gè)節(jié)點(diǎn)的樣本都屬于同一類。

在實(shí)踐中，可能會(huì)形成節(jié)點(diǎn)過多的樹，導(dǎo)致過度擬合。因此，一般情況下會(huì)通過限制樹的最大深度來進(jìn)行剪枝。

信息增益最大化

為了在最具信息的特征分裂節(jié)點(diǎn)，首先必須定義一個(gè)目標(biāo)函數(shù)，并通過樹學(xué)習(xí)算法對(duì)其進(jìn)行優(yōu)化。這里，目標(biāo)函數(shù)是在各個(gè)分裂點(diǎn)處實(shí)現(xiàn)最大化的信息增益，定義如下：

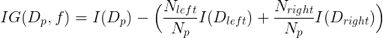
方程式中，f為執(zhí)行分裂的特征，Dp，Dleft和Dright分別為為父子節(jié)點(diǎn)的數(shù)據(jù)集。I為不純性度量，Np為父節(jié)點(diǎn)上樣本的總數(shù)，而Nleft和Nright為子節(jié)點(diǎn)的樣本數(shù)量。

在下面的例子中，本文將更詳細(xì)地討論用于分類和回歸決策樹的不純性度量。但現(xiàn)在，只需理解信息增益簡(jiǎn)單來說就是父節(jié)點(diǎn)不純性和子節(jié)點(diǎn)不純性之和之間的差值，子節(jié)點(diǎn)的不純性越低，則信息增益越大。

注意，上面的方程式只適用于二叉決策樹，即每個(gè)父節(jié)點(diǎn)只分裂為兩個(gè)子節(jié)點(diǎn)。若一個(gè)決策樹包含超過兩個(gè)節(jié)點(diǎn)，那么只需求所有節(jié)點(diǎn)的不純性的總和即可。

分類樹

首先討論分類決策樹（也稱為分類樹）。下面的例子將使用費(fèi)雪鳶尾花卉(iris)數(shù)據(jù)集，機(jī)器學(xué)習(xí)領(lǐng)域的經(jīng)典數(shù)據(jù)集。它包含了來自三個(gè)不同物種的150朵鳶尾花的屬性，分別是Setosa, Versicolor和Virginica。

這些將是本里的目標(biāo)。本例旨在預(yù)測(cè)某個(gè)鳶尾花屬于哪一種類。將花瓣長(zhǎng)度和寬度（以厘米為單位）儲(chǔ)存為列，也稱為該數(shù)據(jù)集的特征。

首先導(dǎo)入數(shù)據(jù)集，并將特征設(shè)為x，目標(biāo)為y：

from sklearn import datasets

iris = datasets.load_iris() # Load iris dataset

X = iris.data[:, [2, 3]] # Assign matrix X

y = iris.target #Assign vector y

使用scikit-learn訓(xùn)練一個(gè)最大深度為4的決策樹。代碼如下：

from sklearn.tree import DecisionTreeClassifier # Import decision tree classifier model

tree = DecisionTreeClassifier(criterion='entropy', # Initialize and fitclassifier

max_depth=4, random_state=1)

tree.fit(X, y)

注意，在這里criterion被設(shè)為‘熵’。該標(biāo)準(zhǔn)被稱為不純性度量（上文有提到）。在分類中，熵是最常見的不純性度量或分裂標(biāo)準(zhǔn)。它的定義如下：

方程式中，p(i|t) 為一個(gè)特定節(jié)點(diǎn)t中屬于c類樣本的部分。因此，如果一個(gè)節(jié)點(diǎn)上的所有樣本都屬于同一類，則熵值為0；如果類型均勻分布，則熵值最大。

為了能更直觀地了解熵，在此編寫類1概率范圍 [0,1] 的不純性指數(shù)。代碼如下：

import numpy as np

import matplotlib.pyplot as plt

def entropy(p):

return - p * np.log2(p) - (1- p) * np.log2(1 - p)

x = np.arange(0.0, 1.0, 0.01) # Create dummy data

e = [entropy(p) if p != 0 else None for p in x] # Calculate entropy

plt.plot(x, e, label='entropy', color='r') # Plot impurity indices

for y in [0.5, 1.0]:

plt.axhline(y=y, linewidth=1,color='k',linestyle='--')

plt.xlabel('p(i=1)')

plt.ylabel('Impurity Index')

plt.legend()

plt.show()

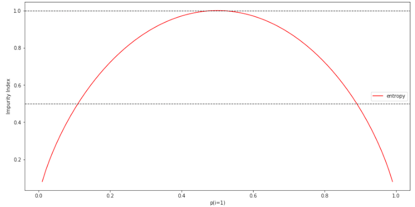
正如所見，當(dāng)p(i=1|t)= 1時(shí)，熵值為0。而當(dāng)所有類型均勻分布，而p(i=1|t)= 0.5時(shí)，熵值為1.

現(xiàn)在回到iris的例子，本文將把訓(xùn)練好的分類樹可視化，然后觀察熵值如何決定每次的分裂。

scikit-learn有一個(gè)很好的功能，它允許用戶在訓(xùn)練之后將決策樹導(dǎo)出為.dot文件，然后可以使用GraphViz之類的軟件將其可視化。除了GraphViz之外，還將使用一個(gè)名為pydotplus的Python庫。它具有類似于GraphViz的功能，可將.dot數(shù)據(jù)文件轉(zhuǎn)換為決策樹圖像文件。

若要安裝pydotplus和graphviz，可在終端執(zhí)行下列指令：

pip3 install pydotplusapt install graphviz

下列代碼可以PNG格式創(chuàng)建本例的決策樹圖像：

from pydotplus.graphviz import graph_from_dot_data

from sklearn.tree import export_graphviz

dot_data = export_graphviz( # Create dot data

tree, filled=True, rounded=True,

class_names=['Setosa','Versicolor','Virginica'],

feature_names=['petallength', 'petal width'],

out_file=None

)

graph = graph_from_dot_data(dot_data) # Create graph from dot data

graph.write_png('tree.png') # Write graphto PNG image

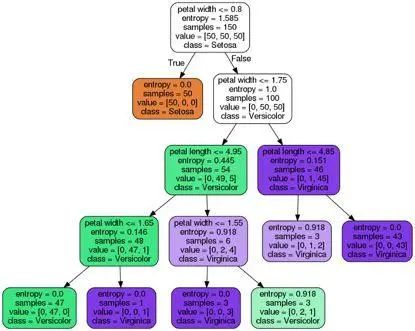
從存在圖像文件tree.png的決策樹圖中，可觀察到?jīng)Q策樹根據(jù)訓(xùn)練數(shù)據(jù)中所進(jìn)行的分裂點(diǎn)。在根節(jié)點(diǎn)處先從150個(gè)樣本開始，然后根據(jù)花瓣寬度是否≤1.75厘米為分裂點(diǎn)，分成兩個(gè)子節(jié)點(diǎn)，各有50和100個(gè)樣本。在第一次分裂后，可看出左子節(jié)點(diǎn)已達(dá)純性，只包含setosa類的樣本（熵值 = 0）。而右邊進(jìn)一步分裂，將樣本分為versicolor和virginica類。

從最終熵值可看出深度為4的決策樹在對(duì)花進(jìn)行分類方面表現(xiàn)得很好。

回歸樹

回歸樹的例子本文將使用波士頓房?jī)r(jià)(Boston Housing)數(shù)據(jù)集。這是另一個(gè)非常流行的數(shù)據(jù)集，包含了波士頓教區(qū)房屋的信息，共有506個(gè)樣本和14個(gè)屬性。

出于簡(jiǎn)化和可視化的考量，這里將只使用兩個(gè)屬性，即MEDV（屋主自住房屋價(jià)值的中位數(shù)，單元為1000美元）為目標(biāo)，LSTAT（地位較低的人口比率）為特征。

首先，將必需的屬性從scikit-learn導(dǎo)入到pandas 數(shù)據(jù)幀DataFrame中。

import pandas as pd

from sklearn import datasets

boston = datasets.load_boston() # Load Boston Dataset

df = pd.DataFrame(boston.data[:, 12]) # Create DataFrame using only the LSATfeature

df.columns = ['LSTAT']

df['MEDV'] = boston.target # Create new column with the targetMEDV

df.head()

使用scikit-learn中的工具DecisionTreeRegressor來訓(xùn)練回歸樹：

from sklearn.tree import DecisionTreeRegressor # Import decision tree regression model

X = df[['LSTAT']].values # Assign matrix X

y = df['MEDV'].values # Assign vector y

sort_idx = X.flatten().argsort() # Sort X and y by ascendingvalues of X

X = X[sort_idx]

y = y[sort_idx]

tree = DecisionTreeRegressor(criterion='mse', # Initialize and fit regressor

max_depth=3)

tree.fit(X, y)

注意，這里的criterion與分類樹中所用的不同。在分類時(shí)，熵作為不純性度量是一個(gè)很有用的標(biāo)準(zhǔn)。然而，若將決策樹用于回歸，則需要一個(gè)適合連續(xù)變量的不純性度量，因此這里使用子節(jié)點(diǎn)的加權(quán)均方誤差 (MSE) 來定義不純性度量：

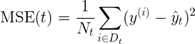
方程式中，Nt為節(jié)點(diǎn)t的訓(xùn)練樣本數(shù)量，Dt為節(jié)點(diǎn)t的訓(xùn)練子集，y(i)為真實(shí)目標(biāo)值，而t為預(yù)測(cè)目標(biāo)值（樣本均值）：

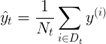
現(xiàn)在，將MEDV和LSTAT之間的關(guān)系進(jìn)行建模，看看回歸樹的直線擬合是什么樣的：

plt.figure(figsize=(16, 8))

plt.scatter(X, y, c='steelblue', # Plot actual target againstfeatures

edgecolor='white',s=70)

plt.plot(X, tree.predict(X), # Plot predicted targetagainst features

color='black', lw=2)

plt.xlabel('% lower status of the population [LSTAT]')

plt.ylabel('Price in $1000s [MEDV]')

plt.show()

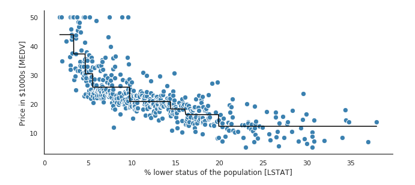
從上圖可看出，深度為3的決策樹就能反映數(shù)據(jù)的總體趨勢(shì)。

本文討論了決策樹的基本概念，最小化不純性的算法，以及如何創(chuàng)建用于分類和回歸的決策樹。

在實(shí)踐中，為樹選擇合適的深度是很重要的，以避免數(shù)據(jù)過度擬合或擬合不足。了解如何將決策樹結(jié)合成整體的隨機(jī)森林也是有益的，基于其隨機(jī)性，通常比單個(gè)決策樹具有更好的泛化性能。這有助于降低模型的方差。此外，它對(duì)數(shù)據(jù)集中的異常值不太敏感，不需要太多的參數(shù)調(diào)優(yōu)。

本文部分素材來源于網(wǎng)絡(luò)，如有侵權(quán)，聯(lián)系刪除。

? ?視頻號(hào)?· 每天一個(gè)小知識(shí)

今日學(xué)習(xí)推薦

【機(jī)器學(xué)習(xí)集訓(xùn)營(yíng)】

線上線下結(jié)合，挑戰(zhàn)年薪 40 萬

零起步--全方位機(jī)器學(xué)習(xí)知識(shí)覆蓋

GPU--全程GPU云平臺(tái)為實(shí)驗(yàn)護(hù)航

重實(shí)戰(zhàn)--全過程實(shí)際工業(yè)項(xiàng)目經(jīng)驗(yàn)

師帶徒--專家級(jí)講師手把手教學(xué)

助內(nèi)推--考點(diǎn)無死角攻破，直推名企

長(zhǎng)按識(shí)別二維碼

咨詢課程

實(shí)戰(zhàn)引導(dǎo)

?

購買，咨詢，查看課程，請(qǐng)點(diǎn)擊【閱讀原文】
↓?↓?↓??