風(fēng)控ML[10] | 風(fēng)控建模中的自動(dòng)分箱的方法有哪些

之前有位讀者朋友說(shuō)有空介紹一下自動(dòng)分箱的方法，這個(gè)確實(shí)在我們實(shí)際建模過(guò)程前是需要解決的一個(gè)問(wèn)題，簡(jiǎn)單來(lái)說(shuō)就是把連續(xù)變量通過(guò)分箱的方式轉(zhuǎn)換為類(lèi)別變量。關(guān)于這個(gè)話題，我也借著這個(gè)主題來(lái)系統(tǒng)的梳理總結(jié)一下幾點(diǎn)：為什么要分箱？不分箱可以入模型嗎？自動(dòng)分箱的常用方法有哪些？評(píng)估分箱效果好壞的方法有哪些？ 如果篇幅允許，就順便把實(shí)現(xiàn)的Python代碼也分享下，如果太長(zhǎng)了就另外起一篇文章來(lái)講。因此，本篇文章主要從下面幾個(gè)模塊來(lái)展開(kāi)說(shuō)說(shuō)。

00 Index

01 分箱是什么意思，為什么要分箱，什么時(shí)候分箱？
02 常見(jiàn)的自動(dòng)分箱方法有哪些？
03 如何評(píng)估分箱效果的好壞
04 設(shè)計(jì)一個(gè)基于風(fēng)控建模的自動(dòng)分箱輪子

01 分箱是什么意思，為什么要分箱，什么時(shí)候分箱？

分箱的意思就是將連續(xù)性變量通過(guò)幾個(gè)劃分點(diǎn)，分割成幾段的過(guò)程。比如說(shuō)我們有一個(gè)字段「年齡」，通過(guò)分箱可以變成：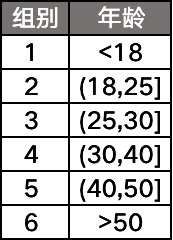

那到了這里有同學(xué)就會(huì)問(wèn)了，為什么要對(duì)連續(xù)性變量進(jìn)行分箱呢？直接拿來(lái)用不行嗎？要回答這個(gè)問(wèn)題，我們先要搞清楚分箱的好處有有哪些，主要有2點(diǎn)：
1）對(duì)變量進(jìn)行分箱后，會(huì)對(duì)異常數(shù)據(jù)有較強(qiáng)的魯棒性，變量會(huì)更加穩(wěn)定；
2）變量分箱后，對(duì)于風(fēng)控建模常用的LR，這種表達(dá)能力有限的線性模型，可以提升模型的表達(dá)能力，加強(qiáng)模型擬合能力。
嗯，講了一些好處，還是有一個(gè)問(wèn)題需要解決的，那就是：不分箱直接使用變量進(jìn)入模型可以嗎？
Actually，對(duì)于風(fēng)控評(píng)分卡的大多數(shù)模型，是可以的，只不過(guò)有些模型，如果直接把連續(xù)變量進(jìn)入模型的話，帶來(lái)的模型效果會(huì)不太理想。那么，下面我將從兩類(lèi)我們常用的風(fēng)控模型來(lái)說(shuō)下：
1）LR：本身屬于線性模型，表達(dá)能力有限，將變量分箱后意味著引入了更多的非線性特征，有助于提升模型擬合能力，一般情況下都進(jìn)行WOE分箱之后再進(jìn)入模型；
2）GBDT：作為Boosting類(lèi)集成分類(lèi)器模型的經(jīng)典，這是一類(lèi)將弱分類(lèi)器提升為強(qiáng)分類(lèi)器的算法，其中的提升樹(shù)（Boosting tree）中間過(guò)程會(huì)產(chǎn)生大量決策樹(shù)，如果輸入的變量是分箱后高稀疏特征的話，一是會(huì)導(dǎo)致模型訓(xùn)練效果過(guò)低，二是會(huì)特別容易過(guò)擬合。一般都是輸入連續(xù)型變量或者是非稀疏的OneHot；
3）XGBoost：它與GBDT類(lèi)似，可以簡(jiǎn)單理解為XGBoost是一種基于GBDT的極度梯度提升的模型，優(yōu)化了正則項(xiàng)和將損失函數(shù)展開(kāi)到二階，在算法精度、訓(xùn)練速度、泛化能力上有較大的優(yōu)化。同GBDT，使用高稀疏的分箱特征入模型的話，速度還是會(huì)比較慢的。
4）CatBoost：CatBoost的主要“賣(mài)點(diǎn)”就是可以直接處理類(lèi)別變量，也就是不需要OneHot直接入模，它也是可以直接對(duì)連續(xù)變量直接使用的；
總的來(lái)說(shuō)，像LR這類(lèi)的線性模型一般都是需要對(duì)連續(xù)變量分箱的，而對(duì)于GBDT、XGBoost這類(lèi)的非線性模型，可以直接輸入連續(xù)變量。

02 常見(jiàn)的自動(dòng)最優(yōu)分箱方法有哪些？

在介紹了分箱的好處以及應(yīng)用的場(chǎng)景后，我們需要知道一些方法去進(jìn)行分箱，最直觀的自動(dòng)分箱方法就是等頻和等距分箱，不過(guò)這類(lèi)過(guò)于簡(jiǎn)單理論的方法，往往效果并不是特別地好。所以今天介紹一下3種業(yè)界常用的自動(dòng)最優(yōu)分箱方法。
1）基于CART算法的連續(xù)變量最優(yōu)分箱
2）基于卡方檢驗(yàn)的連續(xù)變量最優(yōu)分箱
3）基于最優(yōu)KS的連續(xù)變量最優(yōu)分箱

基于CART算法的連續(xù)變量最優(yōu)分箱

回顧一下CART，全稱(chēng)為分類(lèi)與回歸樹(shù)（Classification And Regression Tree），由于CART生成的決策樹(shù)都是二叉決策樹(shù)，并且該算法是基于最小基尼指數(shù)遞歸的方式選擇最優(yōu)的二值劃分點(diǎn)，不斷地把數(shù)據(jù)集劃分成D1和D2兩部分，依此類(lèi)推直到滿(mǎn)足停止條件。
所以連續(xù)分箱也是可以借助相同的理論來(lái)使用，其實(shí)現(xiàn)步驟如下：
1，給定連續(xù)變量 V，對(duì)V中的值進(jìn)行排序；
2，依次計(jì)算相鄰元素間中位數(shù)作為二值劃分點(diǎn)的基尼指數(shù)；
3，選擇最優(yōu)（劃分后基尼指數(shù)下降最大）的劃分點(diǎn)作為本次迭代的劃分點(diǎn)；
4，遞歸迭代步驟2-3，直到滿(mǎn)足停止條件。（一般是以劃分后的樣本量作為停止條件，比如葉子節(jié)點(diǎn)的樣本量>=總樣本量的10%）

基于卡方檢驗(yàn)的連續(xù)變量最優(yōu)分箱

卡方檢驗(yàn)相信很多同學(xué)會(huì)比較熟悉，它是基于卡方分布的一種假設(shè)檢驗(yàn)的方法，主要是用于兩個(gè)分類(lèi)變量之間的獨(dú)立性檢驗(yàn)，其基本思想就是根據(jù)樣本數(shù)據(jù)推斷兩個(gè)分類(lèi)變量是否相互獨(dú)立，其卡方值的計(jì)算公式如下：

其中，A是實(shí)際頻數(shù)，E是期望頻數(shù)。那么這應(yīng)該怎么算呢？可以參考一下下面的例子：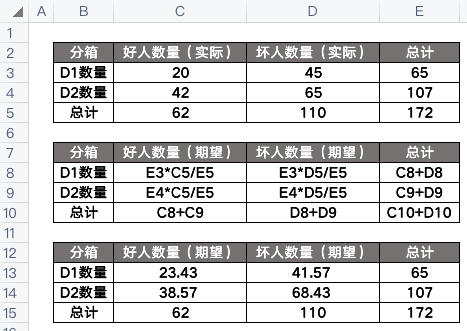

套入上面的公式，算得卡方值為1.26:

這個(gè)卡方值我們可以通過(guò)查找卡方表來(lái)確定是否拒絕原假設(shè)，這里的原假設(shè)是假設(shè)兩個(gè)數(shù)據(jù)集D1和D2沒(méi)有區(qū)別，也就是不需要拆分，可以合并。

import?pandas?as?pd
import?numpy?as?np
from?scipy.stats?import?chi2
p?=?[0.995,?0.990,?0.975,?0.950,?0.900,?0.100,?0.050,?0.025,?0.010,?0.005]
df?=?pd.DataFrame(np.array([chi2.isf(p,?df=i)?for?i?in?range(1,10)]),?columns=p,?index=list(range(1,10)))
df

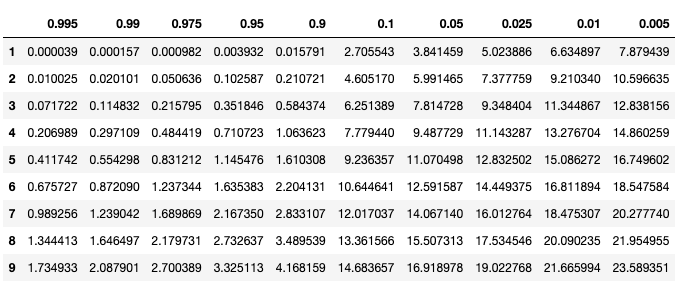
要想讀懂上表，我們需要知道自由度n（縱軸）以及顯著性水平p（橫軸），其中：
自由度n = (行數(shù)-1)* (列數(shù)-1)，上面例子中n = (2-1)* (2-1) = 1，所以我們只需要看表中第一行，而我們算出來(lái)的卡方值是1.26，也就是顯著性水平p介于0.1～0.9之間，p大于0.05，我們就認(rèn)為原假設(shè)成立！ 也就是說(shuō)兩個(gè)數(shù)據(jù)集可以合并！總的來(lái)說(shuō)，就是算出來(lái)的卡方值越小，就越證明這兩個(gè)數(shù)據(jù)集是同一類(lèi)，可以合并。
因此，卡方最優(yōu)分箱的理論基礎(chǔ)就在這兒，卡方分箱算法原名叫ChiMerge算法，分成2階段：初始化階段和自底向上合并階段，主要實(shí)現(xiàn)步驟如下：
1，給定連續(xù)變量 V，對(duì)V中的值進(jìn)行排序，然后每個(gè)元素值單獨(dú)一組，完成初始化階段；
2，對(duì)相鄰的組，兩兩計(jì)算卡方值；
3，合并卡方值最小的兩組；
4，遞歸迭代步驟2-3，直到滿(mǎn)足停止條件。（一般是卡方值都高于設(shè)定的閾值，或者達(dá)到最大分組數(shù)等等）

基于最優(yōu)KS的連續(xù)變量最優(yōu)分箱

KS相信大家也都不陌生，可以稍微回顧下《風(fēng)控建模的KS》 ，不過(guò)這里的KS值不是基于模型計(jì)算的，而是基于變量計(jì)算的，不過(guò)，計(jì)算邏輯和原理都是相通的。

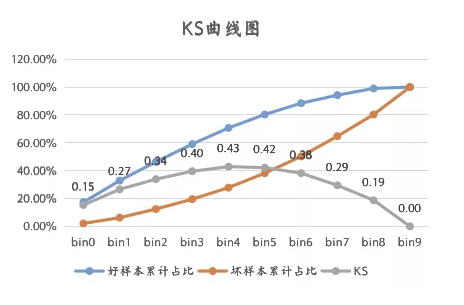所以，我們的最優(yōu)KS分箱方法實(shí)現(xiàn)步驟如下：
1，給定連續(xù)變量 V，對(duì)V中的值進(jìn)行排序；
2，每一個(gè)元素值就是一個(gè)計(jì)算點(diǎn)，對(duì)應(yīng)上圖中的bin0～9；
3，計(jì)算出KS最大的那個(gè)元素，作為最優(yōu)劃分點(diǎn)，將變量劃分成兩部分D1和D2；
4，遞歸迭代步驟3，計(jì)算由步驟3中產(chǎn)生的數(shù)據(jù)集D1 D2的劃分點(diǎn)，直到滿(mǎn)足停止條件。（一般是分箱數(shù)量達(dá)到某個(gè)閾值，或者是KS值小于某個(gè)閾值）
我們需要知道，分箱后的連續(xù)變量，其KS值肯定是比原來(lái)的要小的，所以我們要設(shè)置好停止條件，不然分箱后的變量效果不太好了。

03 如何評(píng)估分箱效果的好壞

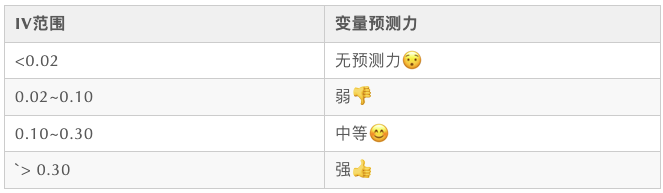
這個(gè)比較簡(jiǎn)單，就是看變量的IV值，具體可以參考之前的一篇文章。《風(fēng)控建模的WOE與IV》

04 設(shè)計(jì)一個(gè)基于風(fēng)控建模的自動(dòng)分箱輪子

一般來(lái)說(shuō)，如果要造一個(gè)基于風(fēng)控建模的連續(xù)變量分箱框架，需要考慮什么內(nèi)容呢？我覺(jué)得應(yīng)該有下面幾點(diǎn)是需要關(guān)注的：
1，最小的分組數(shù)量
2，badrate比例控制
3，缺失值的處理邏輯
4，分箱后IV值計(jì)算與判斷（不能低于0.02）
5，分箱的數(shù)量不能太多，以免太過(guò)于稀疏。
基于上面的考慮，我將會(huì)在未來(lái)設(shè)計(jì)一個(gè)連續(xù)變量自動(dòng)分箱的“輪子”，到時(shí)候把源碼也放出來(lái)，歡迎大家來(lái)補(bǔ)充。

Reference

https://blog.csdn.net/xgxyxs/article/details/90413036
https://zhuanlan.zhihu.com/p/44943177
https://blog.csdn.net/hxcaifly/article/details/84593770
https://blog.csdn.net/haoxun12/article/details/105301414/
https://www.bilibili.com/read/cv12971807