適合初學(xué)者的樹
回復(fù)交流,加入前端編程面試算法每日一題群
引言
不同與我們之前介紹的線性結(jié)構(gòu),今天我們介紹一種非線性結(jié)構(gòu):樹,本章重點(diǎn)介紹樹與二叉樹的基礎(chǔ)必會(huì)內(nèi)容,在開始這一章節(jié)前,請(qǐng)思考以下內(nèi)容:
-
什么是樹? -
什么是二叉樹? -
什么是平衡二叉樹? -
在代碼中如何表示一棵二叉樹? -
二叉樹的前序、中序、后序遍歷又是什么?如何實(shí)現(xiàn)?能否用遞歸及迭代兩種方式實(shí)現(xiàn)喃? -
什么是 BST 樹? -
什么是 AVL 樹? -
什么是紅黑樹? -
什么是 Trie 樹? -
什么是 B 、B+ 樹?
下面進(jìn)入本節(jié)內(nèi)容??
8.1 樹
不同于我們上面介紹的線性結(jié)構(gòu),樹是一種非線性結(jié)構(gòu)。
圖:
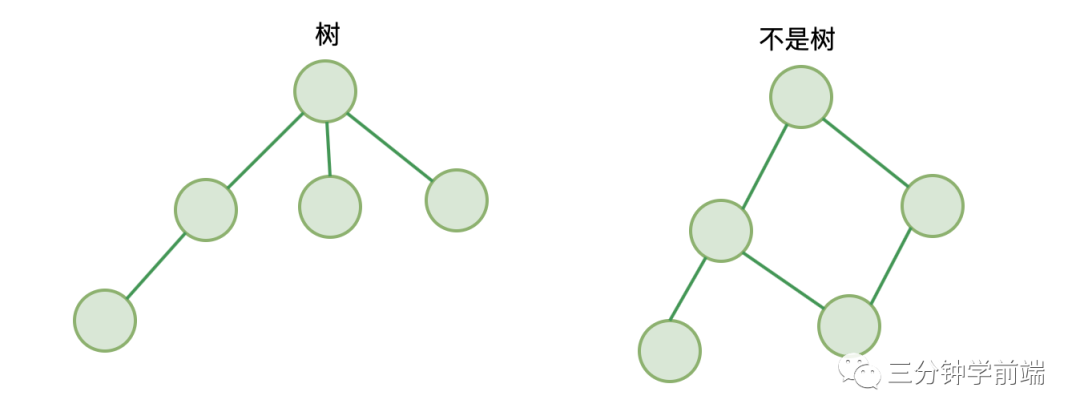
它遵循:
-
僅有唯一一個(gè)根節(jié)點(diǎn),沒有節(jié)點(diǎn)則為空樹 -
除根節(jié)點(diǎn)外,每個(gè)節(jié)點(diǎn)都有并僅有唯一一個(gè)父節(jié)點(diǎn) -
節(jié)點(diǎn)間不能形成閉環(huán)
這就是樹!
樹有幾個(gè)概念:
-
擁有相同父節(jié)點(diǎn)的節(jié)點(diǎn),互稱為兄弟節(jié)點(diǎn) -
節(jié)點(diǎn)的深度 :從根節(jié)點(diǎn)到該節(jié)點(diǎn)所經(jīng)歷的邊的個(gè)數(shù) -
節(jié)點(diǎn)的高度 :節(jié)點(diǎn)到葉節(jié)點(diǎn)的最長(zhǎng)路徑 -
樹的高度:根節(jié)點(diǎn)的高度
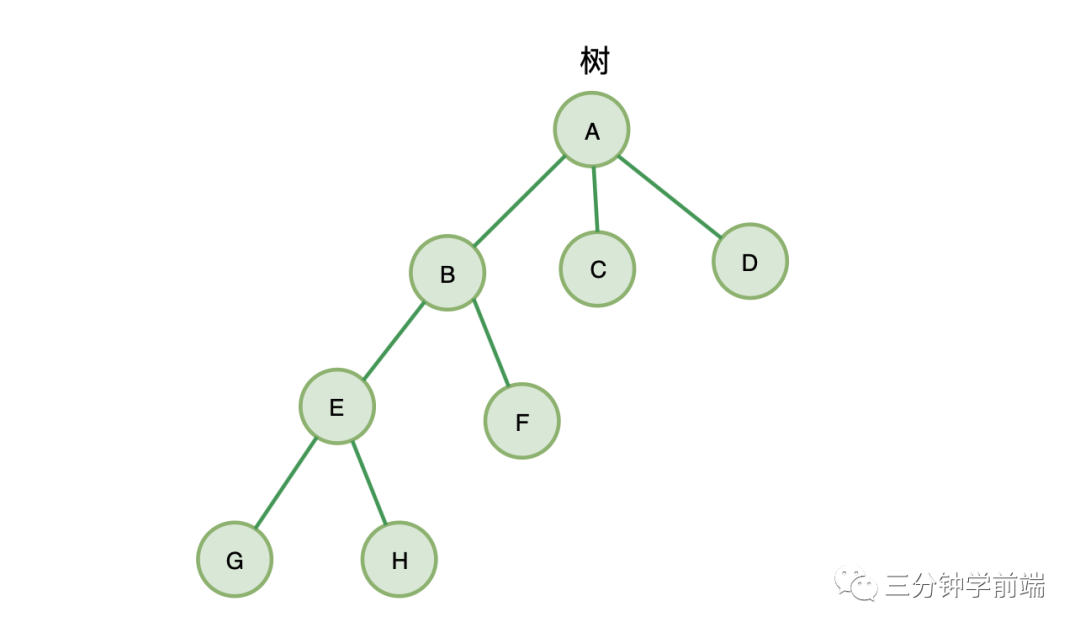
B、C、D就互稱為兄弟節(jié)點(diǎn),其中,節(jié)點(diǎn)B的高度為2,節(jié)點(diǎn)B的深度為 1,樹的高度為3
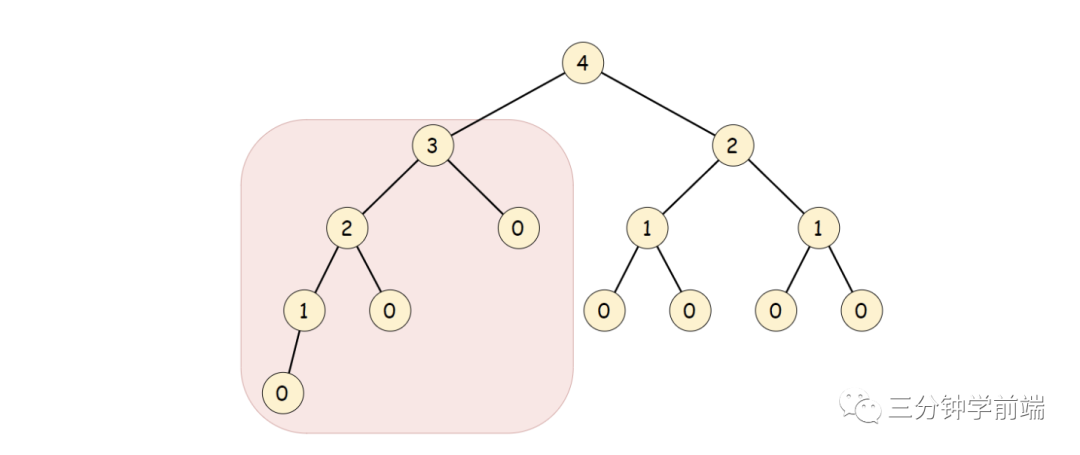
高度
樹的高度計(jì)算公式:

下圖每個(gè)節(jié)點(diǎn)值都代表來當(dāng)前節(jié)點(diǎn)的高度:
8.2 二叉樹
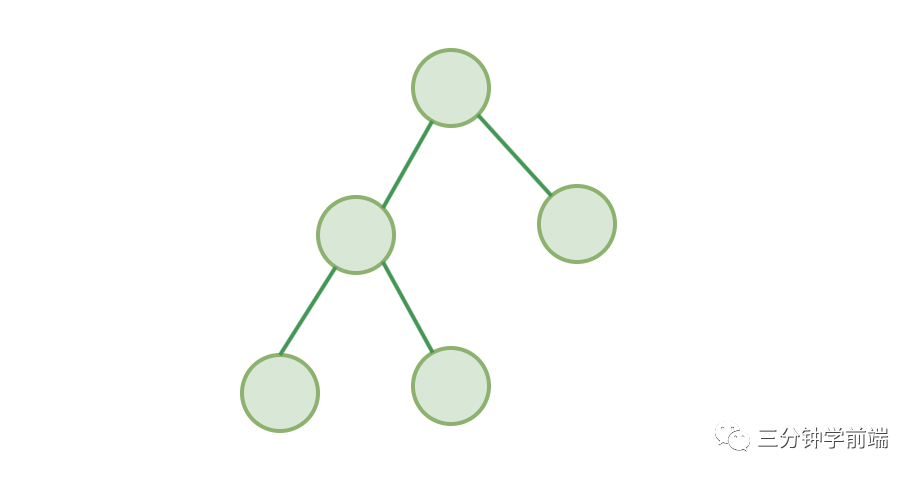
二叉樹,故名思義,最多僅有兩個(gè)子節(jié)點(diǎn)的樹(最多能分兩個(gè)叉的樹???♀?):
圖:
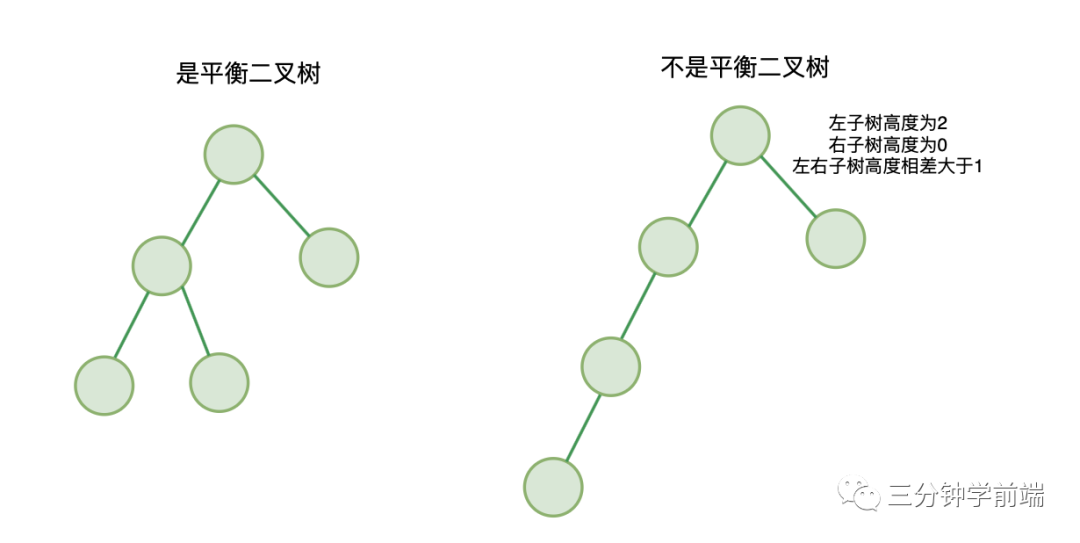
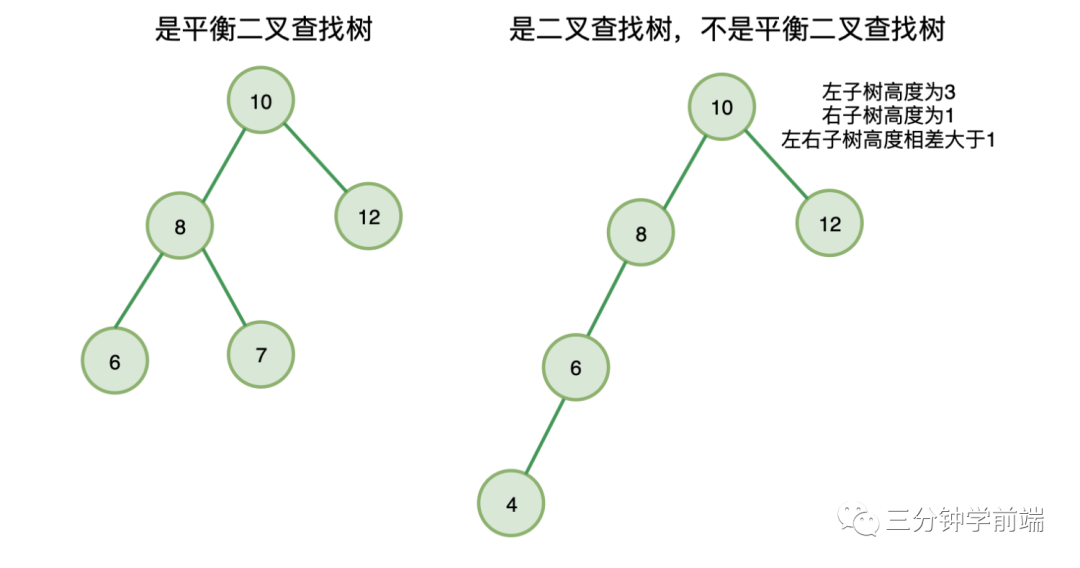
8.3 平衡二叉樹
二叉樹中,每一個(gè)節(jié)點(diǎn)的左右子樹的高度相差不能大于 1,稱為平衡二叉樹。
另外還有滿二叉樹、完全二叉樹等:
-
滿二叉樹:除了葉結(jié)點(diǎn)外每一個(gè)結(jié)點(diǎn)都有左右子葉且葉子結(jié)點(diǎn)都處在最底層的二叉樹 -
完全二叉樹:深度為h,除第 h 層外,其它各層 (1~h-1) 的結(jié)點(diǎn)數(shù)都達(dá)到最大個(gè)數(shù),第h 層所有的結(jié)點(diǎn)都連續(xù)集中在最左邊
8.4 在代碼中如何去表示一棵二叉樹
8.4.1 鏈?zhǔn)酱鎯?chǔ)法
二叉樹的存儲(chǔ)很簡(jiǎn)單,在二叉樹中,我們看到每個(gè)節(jié)點(diǎn)都包含三部分:
-
當(dāng)前節(jié)點(diǎn)的 val -
左子節(jié)點(diǎn) left -
右子節(jié)點(diǎn) right
所以我們可以將每個(gè)節(jié)點(diǎn)定義為:
function Node(val) {
// 保存當(dāng)前節(jié)點(diǎn) key 值
this.val = val
// 指向左子節(jié)點(diǎn)
this.left = null
// 指向右子節(jié)點(diǎn)
this.right = null
}
一棵二叉樹可以由根節(jié)點(diǎn)通過左右指針連接起來形成一個(gè)樹。
function BinaryTree() {
let Node = function (val) {
this.val = val
this.left = null
this.right = null
}
let root = null
}
8.4.2 數(shù)組存儲(chǔ)法(適用于完全二叉樹)
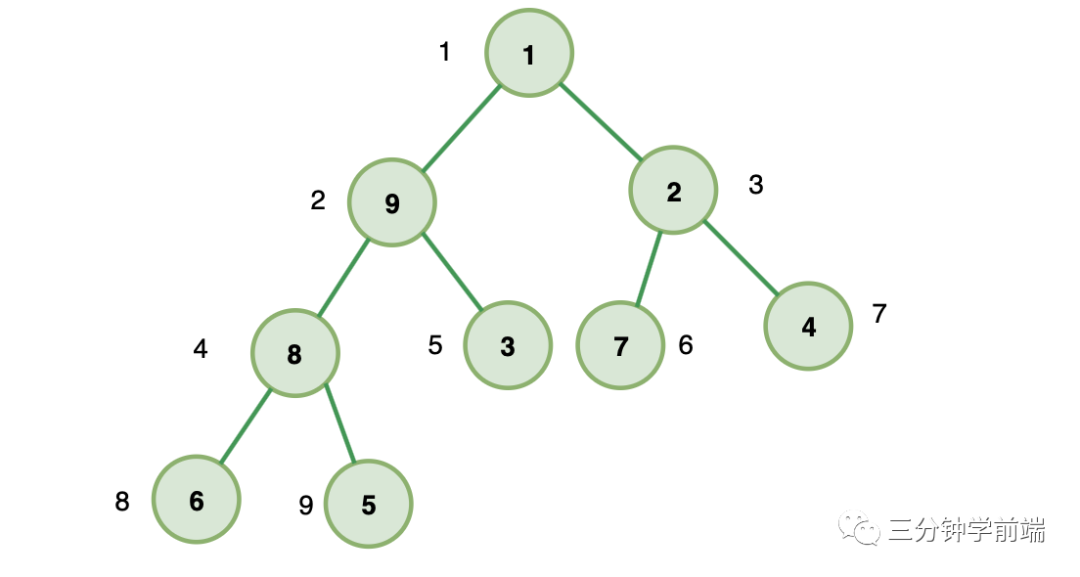
下圖就是一棵完全二叉樹,
如果我們把根節(jié)點(diǎn)存放在位置 i=1 的位置,則它的左子節(jié)點(diǎn)位置為 2i = 2 ,右子節(jié)點(diǎn)位置為 2i+1 = 3 。
如果我們選取 B 節(jié)點(diǎn) i=2 ,則它父節(jié)點(diǎn)為 i/2 = 1 ,左子節(jié)點(diǎn) 2i=4 ,右子節(jié)點(diǎn) 2i+1=5 。
以此類推,我們發(fā)現(xiàn)所有的節(jié)點(diǎn)都滿足這三種關(guān)系:
-
位置為 i 的節(jié)點(diǎn),它的父節(jié)點(diǎn)位置為 i/2 -
它的左子節(jié)點(diǎn) 2i -
它的右子節(jié)點(diǎn) 2i+1
因此,如果我們把完全二叉樹存儲(chǔ)在數(shù)組里(從下標(biāo)為 1 開始存儲(chǔ)),我們完全可以通過下標(biāo)找到任意節(jié)點(diǎn)的父子節(jié)點(diǎn)。從而完整的構(gòu)建出這個(gè)完全二叉樹。這就是數(shù)組存儲(chǔ)法。
數(shù)組存儲(chǔ)法相對(duì)于鏈?zhǔn)酱鎯?chǔ)法不需要為每個(gè)節(jié)點(diǎn)創(chuàng)建它的左右指針,更為節(jié)省內(nèi)存。
8.5 二叉樹的遍歷
二叉樹的遍歷可分為:
-
前序遍歷 -
中序遍歷 -
后序遍歷
所謂前、中、后,不過是根的順序,即也可以稱為先根遍歷、中根遍歷、后根遍歷
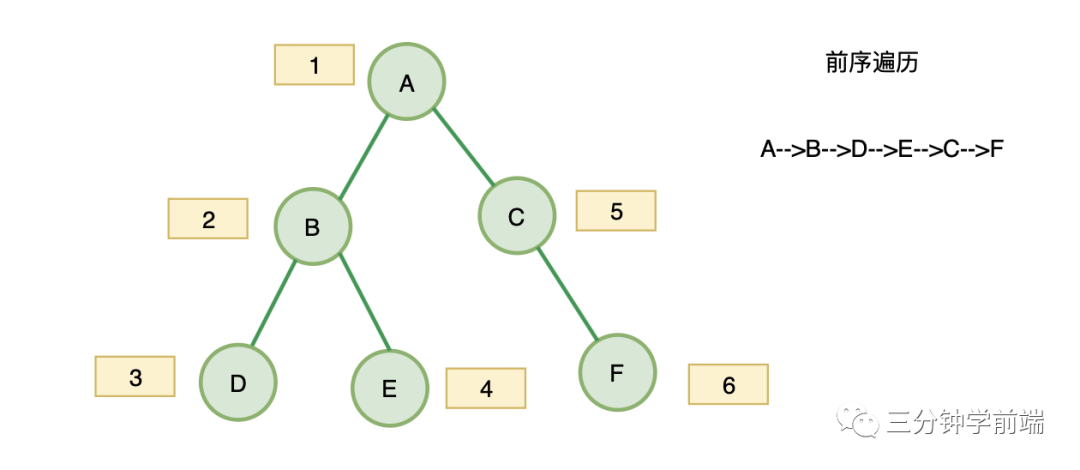
1. 前序遍歷
對(duì)于二叉樹中的任意一個(gè)節(jié)點(diǎn),先打印該節(jié)點(diǎn),然后是它的左子樹,最后右子樹
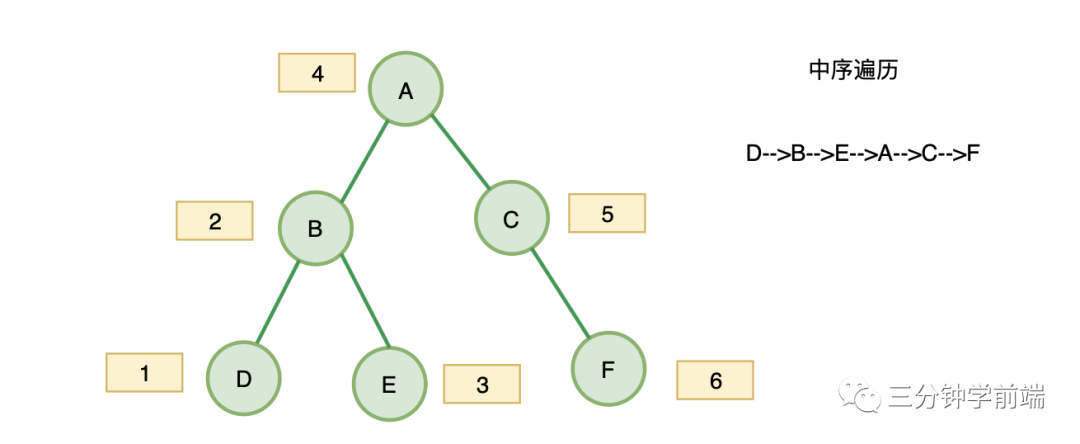
2. 中序遍歷
對(duì)于二叉樹中的任意一個(gè)節(jié)點(diǎn),先打印它的左子樹,然后是該節(jié)點(diǎn),最后右子樹
3. 后序遍歷
對(duì)于二叉樹中的任意一個(gè)節(jié)點(diǎn),先打印它的左子樹,然后是右子樹,最后該節(jié)點(diǎn)

4. 代碼實(shí)現(xiàn)(前序遍歷為例)
所以,遍歷二叉樹的過程也就是一個(gè)遞歸的過程,例如前序遍歷,先遍歷根節(jié)點(diǎn),然后是根的左子樹,最后右子樹;遍歷根節(jié)點(diǎn)的左子樹的時(shí)候,又是先遍歷左子樹的根節(jié)點(diǎn),然后左子樹的左子樹,左子樹的右子樹…….
所以,它的核心代碼就是:
// 前序遍歷核心代碼
const preOrderTraverseNode = (node) => {
if(node) {
// 先根節(jié)點(diǎn)
result.push(node.val)
// 然后遍歷左子樹
preOrderTraverseNode(node.left)
// 再遍歷右子樹
preOrderTraverseNode(node.right)
}
}
完整代碼如下:
遞歸實(shí)現(xiàn)
// 前序遍歷
const preorderTraversal = (root) => {
let result = []
var preOrderTraverseNode = (node) => {
if(node) {
// 先根節(jié)點(diǎn)
result.push(node.val)
// 然后遍歷左子樹
preOrderTraverseNode(node.left)
// 再遍歷右子樹
preOrderTraverseNode(node.right)
}
}
preOrderTraverseNode(root)
return result
};
我們既然可以使用遞歸實(shí)現(xiàn),那么是否也可以使用迭代實(shí)現(xiàn)喃?
迭代實(shí)現(xiàn)
利用棧來記錄遍歷的過程,實(shí)際上,遞歸就使用了調(diào)用棧,所以這里我們可以使用棧來模擬遞歸的過程
-
首先根入棧 -
將根節(jié)點(diǎn)出棧,將根節(jié)點(diǎn)值放入結(jié)果數(shù)組中 -
然后遍歷左子樹、右子樹,因?yàn)闂J窍热牒蟪觯裕覀兿扔易訕淙霔#缓笞笞訕淙霔? -
繼續(xù)出棧(左子樹被出棧)…….
依次循環(huán)出棧遍歷入棧,直到棧為空,遍歷完成
// 前序遍歷
const preorderTraversal = (root) => {
const list = [];
const stack = [];
// 當(dāng)根節(jié)點(diǎn)不為空的時(shí)候,將根節(jié)點(diǎn)入棧
if(root) stack.push(root)
while(stack.length > 0) {
const curNode = stack.pop()
// 第一步的時(shí)候,先訪問的是根節(jié)點(diǎn)
list.push(curNode.val)
// 我們先打印左子樹,然后右子樹
// 所以先加入棧的是右子樹,然后左子樹
if(curNode.right !== null) {
stack.push(curNode.right)
}
if(curNode.left !== null) {
stack.push(curNode.left)
}
}
return list
}
復(fù)雜度分析:
空間復(fù)雜度:O(n)
時(shí)間復(fù)雜度:O(n)
至此,我們已經(jīng)實(shí)現(xiàn)了二叉樹的前序遍歷,嘗試思考一下二叉樹的中序遍歷如何實(shí)現(xiàn)喃?
8.6 二叉查找樹(BST樹)
有的筆者也稱它為二叉搜索樹,都是一個(gè)意思。
二叉樹本身沒有多大的意義,直到有位大佬提出一個(gè) trick。
如果我們規(guī)定一顆二叉樹上的元素?fù)碛许樞颍斜人〉脑卦谒淖笞訕洌人蟮脑卦谒挠易訕洌敲次覀儾痪涂梢院芸斓夭檎夷硞€(gè)元素了嗎?
不得不說這是一個(gè)非常天才的想法,于是,二叉查找樹誕生了。
所以,二叉查找樹與二叉樹不同的是,它在二叉樹的基礎(chǔ)上,增加了對(duì)二叉樹上節(jié)點(diǎn)存儲(chǔ)位置的限制:二叉搜索樹上的每個(gè)節(jié)點(diǎn)都需要滿足:
-
左子節(jié)點(diǎn)值小于該節(jié)點(diǎn)值 -
右子節(jié)點(diǎn)值大于等于該節(jié)點(diǎn)值
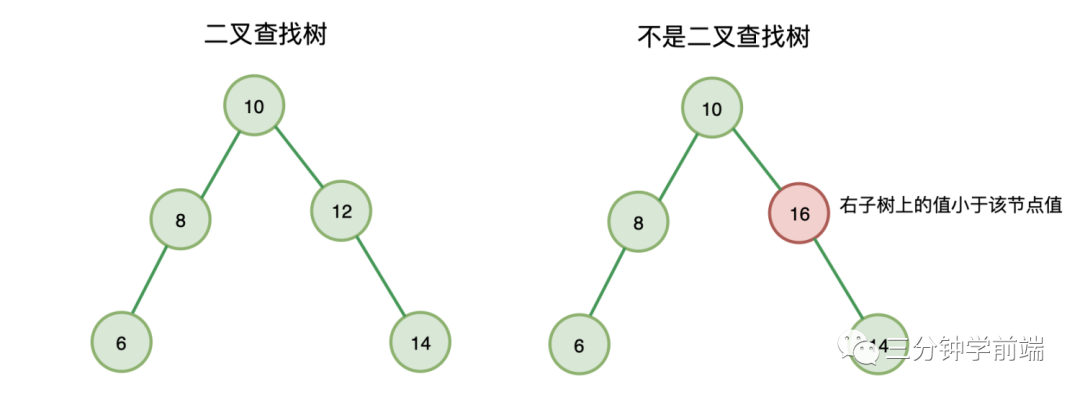
在二叉樹中,所有子節(jié)點(diǎn)值都是沒有固定規(guī)律的,所以使用二叉樹存儲(chǔ)結(jié)構(gòu)存儲(chǔ)數(shù)據(jù)時(shí),查找數(shù)據(jù)的時(shí)間復(fù)雜度為 O(n),因?yàn)樗檎颐恳粋€(gè)節(jié)點(diǎn)。
而使用二叉查找樹就不同了,例如上圖,我們?nèi)绻檎?6 ,先從根節(jié)點(diǎn) 10 比較,6 比 10 小,則查找左子樹,再與 8 比較,6 比 8 小,繼續(xù)查找 8 的左子樹,也就是 6,我們找到了元素,結(jié)束。
8.6.1 基本操作
function BinarySearchTree() {
let Node = function (key) {
this.key = key
this.left = null
this.right = null
}
let root = null
// 插入
this.insert = function(key){}
// 查找
this.search = function(key){}
// 刪除
this.remove = function(key){}
// 最大值
this.max = function(){}
// 最小值
this.min = function(){}
// 中序遍歷
this.inOrderTraverse = function(){}
// 先序遍歷
this.preOrderTraverse = function(){}
// 后序遍歷
this.postOrderTraverse = function(){}
}
插入:
-
首先創(chuàng)建一個(gè)新節(jié)點(diǎn) -
判斷樹是否為空,為空則設(shè)置插入的節(jié)點(diǎn)為根節(jié)點(diǎn),插入成功,返回 -
如果不為空,則比較該節(jié)點(diǎn)與根結(jié)點(diǎn),比根小,插入左子樹,否則插入右子樹
function insert(key) {
// 創(chuàng)建新節(jié)點(diǎn)
let newNode = new Node(key)
// 判斷是否為空樹
if(root === null) {
root = newNode
} else {
insertNode(root, newNode)
}
}
// 將 insertNode 插入到 node 子樹上
function insertNode(node, newNode) {
if(newNode.key < node.key) {
// 插入 node 左子樹
if(node.left === null) {
node.left = newNode
} else {
insertNode(node.left, newNode)
}
} else {
// 插入 node 右子樹
if(node.right === null) {
node.right = newNode
} else {
insertNode(node.right, newNode)
}
}
}
最值:
最小值:樹最左端的節(jié)點(diǎn)
最大值:樹最右端的節(jié)點(diǎn)
// 最小值
function min() {
let node = root
if(node) {
while(node && node.left !== null) {
node = node.left
}
return node.key
}
return null
}
// 最大值
function max() {
let node = root
if(node) {
while(node && node.right !== null) {
node = node.right
}
return node.key
}
return null
}
查找:
function search(key) {
return searchNode(root, key)
}
function searchNode(node, key) {
if(node === null)
return false
if(key < node.key) {
return searchNode(node.left, key)
} else if(key > node.key) {
return searchNode(node.right, key)
} else {
return true
}
}
刪除:
function remove(key) {
root = removeNode(root, key)
}
function removeNode(node, key) {
if(node === null)
return null
if(key < node.key) {
return removeNode(node.left, key)
} else if(key > node.key) {
return removeNode(node.right, key)
} else {
// key = node.key 刪除
//葉子節(jié)點(diǎn)
if(node.left === null && node.right === null) {
node = null
return node
}
// 只有一個(gè)子節(jié)點(diǎn)
if(node.left === null) {
node = node.right
return node
}
if(node.right === null) {
node = node.left
return node
}
// 有兩個(gè)子節(jié)點(diǎn)
// 獲取右子樹的最小值替換當(dāng)前節(jié)點(diǎn)
let minRight = findMinNode(node.right)
node.key = minRight.key
node.right = removeNode(node.right, minRight.key)
return node
}
}
// 獲取 node 樹最小節(jié)點(diǎn)
function findMinNode(node) {
if(node) {
while(node && node.right !== null) {
node = node.right
}
return node
}
return null
}
8.6.2 遍歷
中序遍歷:
顧名思義,中序遍歷就是把根放在中間的遍歷,即按先左節(jié)點(diǎn)、然后根節(jié)點(diǎn)、最后右節(jié)點(diǎn)(左根右)的遍歷方式。
由于BST樹任意節(jié)點(diǎn)都大于左子節(jié)點(diǎn)值小于等于右子節(jié)點(diǎn)值的特性,所以 中序遍歷其實(shí)是對(duì)??進(jìn)行排序操作 ,并且是按從小到大的順序排序。
function inOrderTraverse(callback) {
inOrderTraverseNode(root, callback)
}
function inOrderTraverseNode(node, callback) {
if(node !== null) {
// 先遍歷左子樹
inOrderTraverseNode(node.left, callback)
// 然后根節(jié)點(diǎn)
callback(node.key)
// 再遍歷右子樹
inOrderTraverseNode(node.right, callback)
}
}
// callback 每次將遍歷到的結(jié)果打印到控制臺(tái)
function callback(key) {
console.log(key)
}
先序遍歷:
已經(jīng)實(shí)現(xiàn)的中序遍歷,先序遍歷就很簡(jiǎn)單了,它是按根左右的順序遍歷
function preOrderTraverse() {
preOrderTraverseNode(root, callback)
}
function preOrderTraverseNode(node, callback) {
if(node !== null) {
// 先根節(jié)點(diǎn)
callback(node.key)
// 然后遍歷左子樹
preOrderTraverseNode(node.left, callback)
// 再遍歷右子樹
preOrderTraverseNode(node.right, callback)
}
}
// callback 每次將遍歷到的結(jié)果打印到控制臺(tái)
function callback(key) {
console.log(key)
}
后序遍歷:
后序遍歷按照左右根的順序遍歷,實(shí)現(xiàn)也很簡(jiǎn)單。
function postOrderTraverse() {
postOrderTraverseNode(root, callback)
}
function postOrderTraverseNode(node, callback) {
if(node !== null) {
// 先遍歷左子樹
postOrderTraverseNode(node.left, callback)
// 然后遍歷右子樹
postOrderTraverseNode(node.right, callback)
// 最后根節(jié)點(diǎn)
callback(node.key)
}
}
// callback 每次將遍歷到的結(jié)果打印到控制臺(tái)
function callback(key) {
console.log(key)
}
8.6.3 BST樹的局限
在理想情況下,二叉樹每多一層,可以存儲(chǔ)的元素都增加一倍。也就是說 n 個(gè)元素的二叉搜索樹,對(duì)應(yīng)的樹高為 O(logn)。所以我們查找元素、插入元素的時(shí)間也為 O(logn)。
當(dāng)然這是理想情況下,但在實(shí)際應(yīng)用中,并不是那么理想,例如一直遞增或遞減的給一個(gè)二叉查找樹插入數(shù)據(jù),那么所有插入的元素就會(huì)一直出現(xiàn)在一個(gè)樹的左節(jié)點(diǎn)上,數(shù)型結(jié)構(gòu)就會(huì)退化為鏈表結(jié)構(gòu),時(shí)間復(fù)雜度就會(huì)趨于 O(n),這是不好的。
而我們上面的平衡樹就可以很好的解決這個(gè)問題,所以平衡二叉查找樹(AVL樹,下一章節(jié)探討)由此誕生。
8.7 平衡二叉查找樹(AVL樹)
故名思義,既滿足左右子樹高度不大于 1, 又滿足任意節(jié)點(diǎn)值大于它的左子節(jié)點(diǎn)值,小于等于它的右子節(jié)點(diǎn)值。
AVL 這個(gè)名字的由來,是它的兩個(gè)發(fā)明者G. M. Adelson-Velsky 和 Evgenii Landis 的縮寫,AVL最初是他們兩人在1962 年的論文「An algorithm for the organization of information」中提出來一種數(shù)據(jù)結(jié)構(gòu)
8.8 紅黑樹
紅黑樹也是一種特殊的「二叉查找樹」。
到目前為止我們學(xué)習(xí)的 AVL 樹和即將學(xué)習(xí)的紅黑樹都是二叉查找樹的變體,可見二叉查找樹真的是非常重要基礎(chǔ)二叉樹,如果忘了它的定義可以先回頭看看。
紅黑樹是一種比較難的數(shù)據(jù)結(jié)構(gòu),面試中很少有面試官讓你手寫一個(gè)紅黑樹,最多的話是考察你是否理解紅黑樹,以及為什么有了 AVL 樹還需要紅黑樹,本部分就主要介紹這塊。
8.8.1 什么是紅黑樹
紅黑樹是一種自平衡(并不是絕對(duì)平衡)的二叉查找樹,它除了滿足二分查找樹的特點(diǎn)外,還滿足以下條件:
-
節(jié)點(diǎn)是紅色或黑色 -
根節(jié)點(diǎn)必須是黑色節(jié)點(diǎn) -
所有的葉子節(jié)點(diǎn)都必須是值為 NULL 的黑節(jié)點(diǎn) -
如果一個(gè)節(jié)點(diǎn)是紅色的,則它兩個(gè)子節(jié)點(diǎn)都是黑色的 -
從任一節(jié)點(diǎn)到達(dá)它的每個(gè)葉子節(jié)點(diǎn)的所有的路徑,都有相同數(shù)目的黑色節(jié)點(diǎn)

很多人不理解為神馬要有那么多條條框框,這里引用王爭(zhēng)老師的說法:
我們都玩過魔方吧,其實(shí)魔方的復(fù)原是有固定算法的,遇到哪幾面是什么樣的,你就對(duì)應(yīng)轉(zhuǎn)幾下,只要跟著這個(gè)復(fù)原步驟,最終肯定能把魔方復(fù)原。紅黑樹也是的,它也有固定的條條框框,在插入、刪除時(shí)也有固定的調(diào)整方案。
這些條條框框保證紅黑樹的自平衡,保證紅黑樹從根節(jié)點(diǎn)到達(dá)每一個(gè)葉子節(jié)點(diǎn)的最長(zhǎng)路徑不會(huì)超過最短路徑的 2 倍。
而節(jié)點(diǎn)的路徑長(zhǎng)度決定著對(duì)節(jié)點(diǎn)的查詢效率,這樣我們確保了,最壞情況下的查找、插入、刪除操作的時(shí)間復(fù)雜度不超過 O(logn) ,并且有較高的插入和刪除效率。
8.8.2 紅黑樹 VS 平衡二叉樹(AVL樹)
-
插入和刪除操作,一般認(rèn)為紅黑樹的刪除和插入會(huì)比 AVL 樹更快。因?yàn)椋t黑樹不像 AVL 樹那樣嚴(yán)格的要求平衡因子小于等于1,這就減少了為了達(dá)到平衡而進(jìn)行的旋轉(zhuǎn)操作次數(shù),可以說是犧牲嚴(yán)格平衡性來換取更快的插入和刪除時(shí)間。 -
紅黑樹不要求有不嚴(yán)格的平衡性控制,但是紅黑樹的特點(diǎn),使得任何不平衡都會(huì)在三次旋轉(zhuǎn)之內(nèi)解決。而 AVL 樹如果不平衡,并不會(huì)控制旋轉(zhuǎn)操作次數(shù),旋轉(zhuǎn)直到平衡為止。 -
查找操作,AVL樹的效率更高。因?yàn)?AVL 樹設(shè)計(jì)比紅黑樹更加平衡,不會(huì)出現(xiàn)平衡因子超過 1 的情況,減少了樹的平均搜索長(zhǎng)度。
8.9 Trie 樹
8.9.1 什么是 Trie 樹
Trie 樹,也稱為字典樹或前綴樹,顧名思義,它是用來處理字符串匹配問題的數(shù)據(jù)結(jié)構(gòu),以及用來解決集合中查找固定前綴字符串的數(shù)據(jù)結(jié)構(gòu)。
8.9.2 Trie樹的應(yīng)用:字符串匹配
在搜索引擎中輸入關(guān)鍵字,搜索引擎都會(huì)彈出下拉框,顯示各種關(guān)鍵字提示,例如必應(yīng):
必應(yīng)是如何處理這一過程的喃?
或者,假設(shè)我們有n個(gè)單詞的數(shù)據(jù)集,任意輸入一串字符,如何在數(shù)據(jù)集中快速匹配出具有輸入字符前綴的單詞?
這樣類似的問題還有很多,在日常開發(fā)中,遇到類似的問題,我們應(yīng)該如何去處理?選擇怎樣的數(shù)據(jù)結(jié)構(gòu)與算法?尤其是遇到大規(guī)模數(shù)據(jù)時(shí),如何更高效的處理?
最簡(jiǎn)單的方法就是暴力,將數(shù)據(jù)集中的每個(gè)字符串,逐個(gè)字符的匹配輸入字符,所有字符都匹配上則前綴匹配成功。這種方式也是我們開發(fā)當(dāng)中最常用,最簡(jiǎn)單的方式,時(shí)間復(fù)雜度為 O(m*n) ,其中 m 為輸入字符串長(zhǎng)度, n 為數(shù)據(jù)集規(guī)模。
這個(gè)時(shí)間復(fù)雜度是很高的,當(dāng) n 很大時(shí),暴力法性能就會(huì)很差,此時(shí)必須重新尋找合適的算法。
我們知道在樹上查找、插入都比較方便,一般時(shí)間復(fù)雜度只與樹的高度相關(guān),我們可以通過樹結(jié)構(gòu)來處理,也就是我們要說的 Trie 樹。其實(shí),引擎搜索關(guān)鍵字提示底層也是通過 Trie 樹實(shí)現(xiàn)的。
舉個(gè)例子:假設(shè)數(shù)據(jù)集有:are 、 add 、 adopt 、set 、so ,它構(gòu)鍵過程:
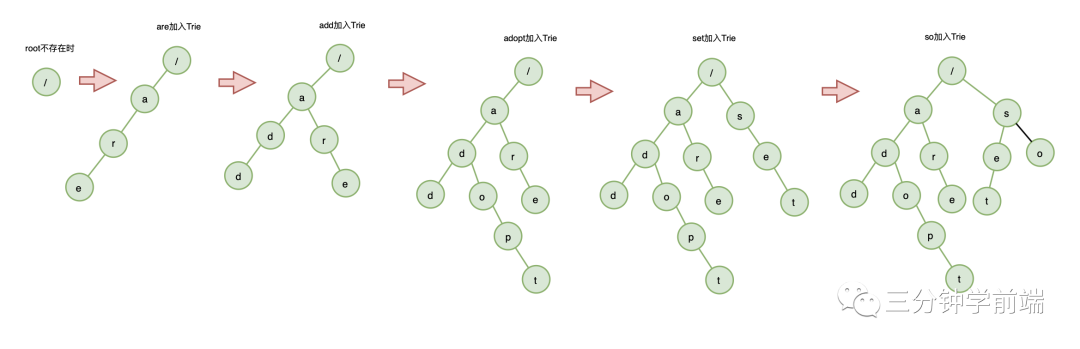
當(dāng)所以的字符串插入完成,Trie樹就構(gòu)建完成了。
Trie樹的本質(zhì)是利用字符串的公共前綴,將重復(fù)的前綴合并在一起,其中根節(jié)點(diǎn)不包含任何信息,每個(gè)節(jié)點(diǎn)表示一個(gè)字符串中的字符,從根節(jié)點(diǎn)到葉節(jié)點(diǎn)的路徑,表示一個(gè)字符串。
在字符串匹配的時(shí)候,我們只要按照樹的結(jié)構(gòu)從上到下匹配即可。
8.10 B 樹、B+ 樹(感興趣進(jìn))
8.10.1 多叉查找樹
既然二叉查找樹已經(jīng)理解了,那多叉查找樹就很好理解了,它與二叉查找樹唯一不同的是,它是多叉的。也就是說,多叉查找樹允許一個(gè)節(jié)點(diǎn)存儲(chǔ)多個(gè)元素,并且可以擁有多個(gè)子樹。
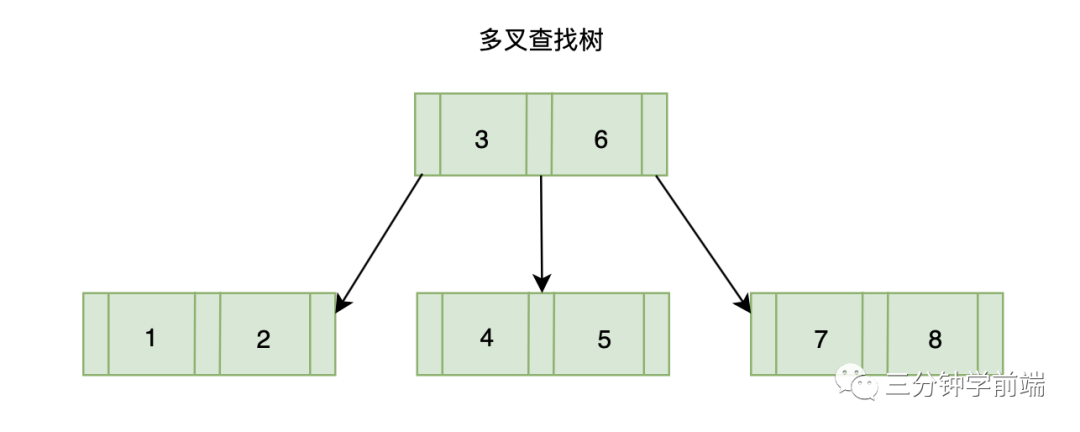
為什么在有二叉查找樹的情況下,還要有多叉查找樹喃?
我們知道樹的深度越高,時(shí)間復(fù)雜度越高,性能越差,多叉查找樹相對(duì)于二叉查找樹來說,每個(gè)節(jié)點(diǎn)不止能擁有兩個(gè)子節(jié)點(diǎn),每層存放的節(jié)點(diǎn)數(shù)可比二叉查找樹多,自然多叉查找樹的的深度就要更小,性能也就更好。例如主要用于各大存儲(chǔ)文件系統(tǒng)與數(shù)據(jù)庫系統(tǒng)中的 B 樹。
8.10.2 B 樹(B-tree)
B 樹,又稱平衡多叉查找樹。它是一種自平衡的多叉查找樹。
如果一棵多路查找樹滿足以下規(guī)則,則稱之為 B 樹:
-
排序方式:所有節(jié)點(diǎn)關(guān)鍵字是按遞增次序排列,并遵循左小右大原則; -
子節(jié)點(diǎn)數(shù):非葉節(jié)點(diǎn)的子節(jié)點(diǎn)數(shù)>1,且<=M ,且M>=2,空樹除外(注:M階代表一個(gè)樹節(jié)點(diǎn)最多有多少個(gè)查找路徑,M=M叉(或路),當(dāng)M=2則是2叉樹,M=3則是3叉); -
關(guān)鍵字?jǐn)?shù):枝節(jié)點(diǎn)(非根非葉)的關(guān)鍵字?jǐn)?shù)量(K)應(yīng)滿足 (M+1)/2 < K < M -
所有葉子節(jié)點(diǎn)均在同一層、葉子節(jié)點(diǎn)除了包含了關(guān)鍵字和關(guān)鍵字記錄的指針外也有指向其子節(jié)點(diǎn)的指針只不過其指針地址都為null對(duì)應(yīng)下圖最后一層節(jié)點(diǎn)的空格子;
最后,我們使用一張圖加深一下理解:

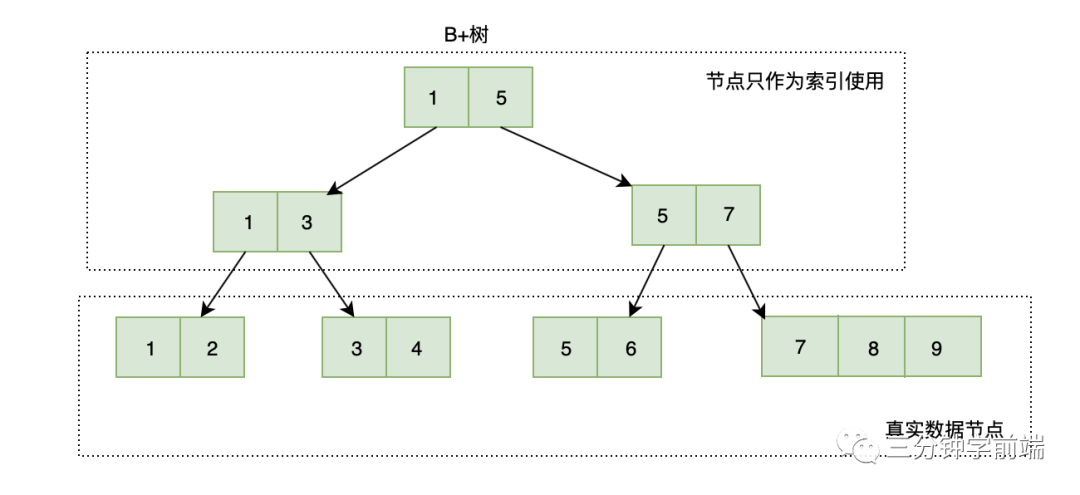
8.10.3 B+樹
B+樹與B樹一樣都是多叉平衡查找樹(又名多路平衡查找樹),B+樹與B樹不同的是:
-
B+樹改進(jìn)了B樹,讓內(nèi)結(jié)點(diǎn)(非葉節(jié)點(diǎn))只作索引使用,去掉了其中指向data的指針,使得每個(gè)結(jié)點(diǎn)中能夠存放更多的key, 因此能有更大的出度。
這有什么用?這樣就意味著存放同樣多的key,樹的層高能進(jìn)一步被壓縮,使得檢索的時(shí)間更短
-
中間節(jié)點(diǎn)的元素?cái)?shù)量與子樹一致,而B樹子樹數(shù)量與元素?cái)?shù)量多1
-
葉子節(jié)點(diǎn)是一個(gè)鏈表,可以通過指針順序查找
8.11 加深
8.11.1 二叉樹的中序遍歷
遞歸實(shí)現(xiàn):
// 中序遍歷
const inorderTraversal = (root) => {
let result = []
var inorderTraversal = (node) => {
if(node) {
// 先遍歷左子樹
inorderTraversal(node.left)
// 再根節(jié)點(diǎn)
result.push(node.val)
// 最后遍歷右子樹
inorderTraversal(node.right)
}
}
inorderTraversal(root)
return result
};
迭代實(shí)現(xiàn):
const inorderTraversal = function(root) {
let list = []
let stack = []
let node = root
while(stack.length || node) {
if(node) {
stack.push(node)
node = node.left
continue
}
node = stack.pop()
list.push(node.val)
node = node.right
}
return list
};
進(jìn)一步簡(jiǎn)化:
// 中序遍歷
const inorderTraversal = (root) => {
let list = []
let stack = []
let node = root
while(node || stack.length) {
// 遍歷左子樹
while(node) {
stack.push(node)
node = node.left
}
node = stack.pop()
list.push(node.val)
node = node.right
}
return list
}
復(fù)雜度分析:
-
空間復(fù)雜度:O(n) -
時(shí)間復(fù)雜度:O(n)
更多解答
8.11.2 二叉樹的后序遍歷
遞歸實(shí)現(xiàn)
// 后序遍歷
const postorderTraversal = function(root) {
let result = []
var postorderTraversalNode = (node) => {
if(node) {
// 先遍歷左子樹
postorderTraversalNode(node.left)
// 再遍歷右子樹
postorderTraversalNode(node.right)
// 最后根節(jié)點(diǎn)
result.push(node.val)
}
}
postorderTraversalNode(root)
return result
};
迭代實(shí)現(xiàn)
解題思路: 后序遍歷與前序遍歷不同的是:
-
后序遍歷是左右根 -
而前序遍歷是根左右
如果我們把前序遍歷的 list.push(node.val) 變更為 list.unshift(node.val) (遍歷結(jié)果逆序),那么遍歷順序就由 根左右 變更為 右左根
然后我們僅需將 右左根 變更為 左右根 即可完成后序遍
// 后序遍歷
const postorderTraversal = (root) => {
const list = [];
const stack = [];
// 當(dāng)根節(jié)點(diǎn)不為空的時(shí)候,將根節(jié)點(diǎn)入棧
if(root) stack.push(root)
while(stack.length > 0) {
const node = stack.pop()
// 根左右=>右左根
list.unshift(node.val)
// 先進(jìn)棧左子樹后右子樹
// 出棧的順序就變更為先右后左
// 右先頭插法入list
// 左再頭插法入list
// 實(shí)現(xiàn)右左根=>左右根
if(node.left !== null) {
stack.push(node.left)
}
if(node.right !== null) {
stack.push(node.right)
}
}
return list
}
復(fù)雜度分析:
-
空間復(fù)雜度:O(n) -
時(shí)間復(fù)雜度:O(n)
更多解答
8.11.3 二叉樹的層次遍歷
給定一個(gè)二叉樹,返回其節(jié)點(diǎn)值自底向上的層次遍歷。(即按從葉子節(jié)點(diǎn)所在層到根節(jié)點(diǎn)所在的層,逐層從左向右遍歷)
例如:給定二叉樹 [3,9,20,null,null,15,7] ,
3
/ \
9 20
/ \
15 7
返回其自底向上的層次遍歷為:
[
[15,7],
[9,20],
[3]
]
解法一:BFS(廣度優(yōu)先遍歷)
BFS 是按層層推進(jìn)的方式,遍歷每一層的節(jié)點(diǎn)。題目要求的是返回每一層的節(jié)點(diǎn)值,所以這題用 BFS 來做非常合適。BFS 需要用隊(duì)列作為輔助結(jié)構(gòu),我們先將根節(jié)點(diǎn)放到隊(duì)列中,然后不斷遍歷隊(duì)列。
const levelOrderBottom = function(root) {
if(!root) return []
let res = [],
queue = [root]
while(queue.length) {
let curr = [],
temp = []
while(queue.length) {
let node = queue.shift()
curr.push(node.val)
if(node.left) temp.push(node.left)
if(node.right) temp.push(node.right)
}
res.push(curr)
queue = temp
}
return res.reverse()
};
復(fù)雜度分析
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(n)
解法二:DFS(深度優(yōu)先遍歷)
DFS 是沿著樹的深度遍歷樹的節(jié)點(diǎn),盡可能深地搜索樹的分支
DFS 做本題的主要問題是:DFS 不是按照層次遍歷的。為了讓遞歸的過程中同一層的節(jié)點(diǎn)放到同一個(gè)列表中,在遞歸時(shí)要記錄每個(gè)節(jié)點(diǎn)的深度 depth 。遞歸到新節(jié)點(diǎn)要把該節(jié)點(diǎn)放入 depth 對(duì)應(yīng)列表的末尾。
當(dāng)遍歷到一個(gè)新的深度 depth ,而最終結(jié)果 res 中還沒有創(chuàng)建 depth 對(duì)應(yīng)的列表時(shí),應(yīng)該在 res 中新建一個(gè)列表用來保存該 depth 的所有節(jié)點(diǎn)。
const levelOrderBottom = function(root) {
const res = []
var dep = function (node, depth){
if(!node) return
res[depth] = res[depth]||[]
res[depth].push(node.val)
dep(node.left, depth + 1)
dep(node.right, depth + 1)
}
dep(root, 0)
return res.reverse()
};
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(h),h為樹的高度
更多解答
8.11.4 二叉樹的層序遍歷
給你一個(gè)二叉樹,請(qǐng)你返回其按 層序遍歷 得到的節(jié)點(diǎn)值。(即逐層地,從左到右訪問所有節(jié)點(diǎn))。
示例:二叉樹:[3,9,20,null,null,15,7] ,
3
/ \
9 20
/ \
15 7
返回其層次遍歷結(jié)果:
[
[3],
[9,20],
[15,7]
]
感謝 @plane-hjh 的解答:
這道題和二叉樹的層次遍歷相似,只需要把 reverse() 去除就可以了
廣度優(yōu)先遍歷
const levelOrder = function(root) {
if(!root) return []
let res = [],
queue = [root]
while(queue.length) {
let curr = [],
temp = []
while(queue.length) {
let node = queue.shift()
curr.push(node.val)
if(node.left) temp.push(node.left)
if(node.right) temp.push(node.right)
}
res.push(curr)
queue = temp
}
return res
};
深度優(yōu)先遍歷
const levelOrder = function(root) {
const res = []
var dep = function (node, depth){
if(!node) return
res[depth] = res[depth]||[]
res[depth].push(node.val)
dep(node.left, depth + 1)
dep(node.right, depth + 1)
}
dep(root, 0)
return res
};
更多解答
8.11.5 重構(gòu)二叉樹:從前序與中序遍歷序列構(gòu)造二叉樹
輸入某二叉樹的前序遍歷和中序遍歷的結(jié)果,請(qǐng)重建該二叉樹。假設(shè)輸入的前序遍歷和中序遍歷的結(jié)果中都不含重復(fù)的數(shù)字。
注意:你可以假設(shè)樹中沒有重復(fù)的元素。
例如,給出
前序遍歷 preorder = [3,9,20,15,7]
中序遍歷 inorder = [9,3,15,20,7]
返回如下的二叉樹:
3
/ \
9 20
/ \
15 7
限制:
0 <= 節(jié)點(diǎn)個(gè)數(shù) <= 5000
推薦 @luweiCN 的解答:
仔細(xì)分析前序遍歷和中序遍歷可以知道(以題目為例):
-
前序遍歷的第一個(gè)元素一定是根節(jié)點(diǎn),這里是 3 -
找到根節(jié)點(diǎn)之后,根節(jié)點(diǎn)在中序遍歷中把數(shù)組一分為二,即兩個(gè)數(shù)組 [9]和[15, 20, 7],這兩個(gè)數(shù)組分別是根節(jié)點(diǎn)3的左子樹和右子樹的中序遍歷。 -
前序遍歷數(shù)組去掉根節(jié)點(diǎn)之后是 [9,20,15,7],而這個(gè)數(shù)組的第1項(xiàng)[9](左子樹的大小)和后3項(xiàng)[20, 15, 7](右子樹的大小)又分別是左子樹和右子樹的前序遍歷 到這里已經(jīng)很明顯了,用遞歸
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
const buildTree = function (preorder, inorder) {
if (preorder.length) {
let head = new TreeNode(preorder.shift());
let index = inorder.indexOf(head.val);
head.left = buildTree(
preorder.slice(0, index),
inorder.slice(0, index)
);
head.right = buildTree(preorder.slice(index), inorder.slice(index + 1));
// 這里要注意,preorder前面shift一次長(zhǎng)度比inorder小1
return head;
} else {
return null;
}
};
更多解答
8.11.6 二叉樹的最大深度
給定一個(gè)二叉樹,找出其最大深度。
二叉樹的深度為根節(jié)點(diǎn)到最遠(yuǎn)葉子節(jié)點(diǎn)的最長(zhǎng)路徑上的節(jié)點(diǎn)數(shù)。
說明: 葉子節(jié)點(diǎn)是指沒有子節(jié)點(diǎn)的節(jié)點(diǎn)。
示例:給定二叉樹 [3,9,20,null,null,15,7] ,
3
/ \
9 20
/ \
15 7
返回它的最大深度 3
解答:遞歸
const maxDepth = function(root) {
if(!root) return 0
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right))
};
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(log?n)
更多解答
8.11.7 二叉樹的最近公共祖先
給定一個(gè)二叉樹, 找到該樹中兩個(gè)指定節(jié)點(diǎn)的最近公共祖先。
百度百科中最近公共祖先的定義為:“對(duì)于有根樹 T 的兩個(gè)結(jié)點(diǎn) p、q,最近公共祖先表示為一個(gè)結(jié)點(diǎn) x,滿足 x 是 p、q 的祖先且 x 的深度盡可能大(一個(gè)節(jié)點(diǎn)也可以是它自己的祖先)。”
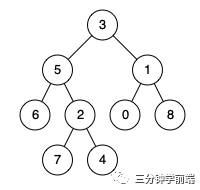
例如,給定如下二叉樹: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
輸出: 3
解釋: 節(jié)點(diǎn) 5 和節(jié)點(diǎn) 1 的最近公共祖先是節(jié)點(diǎn) 3。
示例 2:
輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
輸出: 5
解釋: 節(jié)點(diǎn) 5 和節(jié)點(diǎn) 4 的最近公共祖先是節(jié)點(diǎn) 5。因?yàn)楦鶕?jù)定義最近公共祖先節(jié)點(diǎn)可以為節(jié)點(diǎn)本身。
說明:
-
所有節(jié)點(diǎn)的值都是唯一的。 -
p、q 為不同節(jié)點(diǎn)且均存在于給定的二叉樹中。
解答:遞歸實(shí)現(xiàn)
解題思路:
如果樹為空樹或 p 、 q 中任一節(jié)點(diǎn)為根節(jié)點(diǎn),那么 p 、 q 的最近公共節(jié)點(diǎn)為根節(jié)點(diǎn)
如果不是,即二叉樹不為空樹,且 p 、 q 為非根節(jié)點(diǎn),則遞歸遍歷左右子樹,獲取左右子樹的最近公共祖先,
-
如果 p、q節(jié)點(diǎn)在左右子樹的最近公共祖先都存在,說明p、q節(jié)點(diǎn)分布在左右子樹的根節(jié)點(diǎn)上,此時(shí)二叉樹的最近公共祖先為root -
若 p、q節(jié)點(diǎn)在左子樹最近公共祖先為空,那p、q節(jié)點(diǎn)位于左子樹上,最終二叉樹的最近公共祖先為右子樹上p、q節(jié)點(diǎn)的最近公共祖先 -
若 p、q節(jié)點(diǎn)在右子樹最近公共祖先為空,同左子樹p、q節(jié)點(diǎn)的最近公共祖先為空一樣的判定邏輯 -
如果 p、q節(jié)點(diǎn)在左右子樹的最近公共祖先都為空,則返回null
代碼實(shí)現(xiàn):
const lowestCommonAncestor = function(root, p, q) {
if(root == null || root == p || root == q) return root
const left = lowestCommonAncestor(root.left, p, q)
const right = lowestCommonAncestor(root.right, p, q)
if(left === null) return right
if(right === null) return left
return root
};
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(n)
更多解答
8.11.8 平衡二叉樹
給定一個(gè)二叉樹,判斷它是否是高度平衡的二叉樹。
本題中,一棵高度平衡二叉樹定義為:
一個(gè)二叉樹每個(gè)節(jié)點(diǎn) 的左右兩個(gè)子樹的高度差的絕對(duì)值不超過1。
示例 1:
給定二叉樹 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
返回 true 。
示例 2:
給定二叉樹 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/ \
4 4
返回 false 。
解答一:自頂向下(暴力法)
解題思路: 自頂向下的比較每個(gè)節(jié)點(diǎn)的左右子樹的最大高度差,如果二叉樹中每個(gè)節(jié)點(diǎn)的左右子樹最大高度差小于等于 1 ,即每個(gè)子樹都平衡時(shí),此時(shí)二叉樹才是平衡二叉樹
代碼實(shí)現(xiàn):
const isBalanced = function (root) {
if(!root) return true
return Math.abs(depth(root.left) - depth(root.right)) <= 1
&& isBalanced(root.left)
&& isBalanced(root.right)
}
const depth = function (node) {
if(!node) return -1
return 1 + Math.max(depth(node.left), depth(node.right))
}
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(nlogn),計(jì)算 depth存在大量冗余操作 -
空間復(fù)雜度:O(n)
解答二:自底向上(優(yōu)化)
解題思路: 利用后續(xù)遍歷二叉樹(左右根),從底至頂返回子樹最大高度,判定每個(gè)子樹是不是平衡樹 ,如果平衡,則使用它們的高度判斷父節(jié)點(diǎn)是否平衡,并計(jì)算父節(jié)點(diǎn)的高度,如果不平衡,返回 -1 。
遍歷比較二叉樹每個(gè)節(jié)點(diǎn) 的左右子樹深度:
-
比較左右子樹的深度,若差值大于 1則返回一個(gè)標(biāo)記-1,表示當(dāng)前子樹不平衡 -
左右子樹有一個(gè)不是平衡的,或左右子樹差值大于 1,則二叉樹不平衡 -
若左右子樹平衡,返回當(dāng)前樹的深度(左右子樹的深度最大值 +1)
代碼實(shí)現(xiàn):
const isBalanced = function (root) {
return balanced(root) !== -1
};
const balanced = function (node) {
if (!node) return 0
const left = balanced(node.left)
const right = balanced(node.right)
if (left === -1 || right === -1 || Math.abs(left - right) > 1) {
return -1
}
return Math.max(left, right) + 1
}
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(n)
更多解答
8.11.9 路徑總和
給定一個(gè)二叉樹和一個(gè)目標(biāo)和,判斷該樹中是否存在根節(jié)點(diǎn)到葉子節(jié)點(diǎn)的路徑,這條路徑上所有節(jié)點(diǎn)值相加等于目標(biāo)和。
說明: 葉子節(jié)點(diǎn)是指沒有子節(jié)點(diǎn)的節(jié)點(diǎn)。
示例: 給定如下二叉樹,以及目標(biāo)和 sum = 22 ,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true , 因?yàn)榇嬖谀繕?biāo)和為 22 的根節(jié)點(diǎn)到葉子節(jié)點(diǎn)的路徑 5->4->11->2。
解題思路:
只需要遍歷整棵樹
-
如果當(dāng)前節(jié)點(diǎn)不是葉子節(jié)點(diǎn),遞歸它的所有子節(jié)點(diǎn),傳遞的參數(shù)就是 sum 減去當(dāng)前的節(jié)點(diǎn)值; -
如果當(dāng)前節(jié)點(diǎn)是葉子節(jié)點(diǎn),判斷參數(shù) sum 是否等于當(dāng)前節(jié)點(diǎn)值,如果相等就返回 true,否則返回 false。
代碼實(shí)現(xiàn):
var hasPathSum = function(root, sum) {
// 根節(jié)點(diǎn)為空
if (root === null) return false;
// 葉節(jié)點(diǎn) 同時(shí) sum 參數(shù)等于葉節(jié)點(diǎn)值
if (root.left === null && root.right === null) return root.val === sum;
// 總和減去當(dāng)前值,并遞歸
sum = sum - root.val
return hasPathSum(root.left, sum) || hasPathSum(root.right, sum);
};
更多解答
8.11.10 對(duì)稱二叉樹
給定一個(gè)二叉樹,檢查它是否是鏡像對(duì)稱的。
例如,二叉樹 [1,2,2,3,4,4,3] 是對(duì)稱的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面這個(gè) [1,2,2,null,3,null,3] 則不是鏡像對(duì)稱的:
1
/ \
2 2
\ \
3 3
進(jìn)階:
你可以運(yùn)用遞歸和迭代兩種方法解決這個(gè)問題嗎?
解答:
一棵二叉樹對(duì)稱,則需要滿足:根的左右子樹是鏡像對(duì)稱的
也就是說,每棵樹的左子樹都和另外一顆樹的右子樹鏡像對(duì)稱,左子樹的根節(jié)點(diǎn)值與右子樹的根節(jié)點(diǎn)值相等
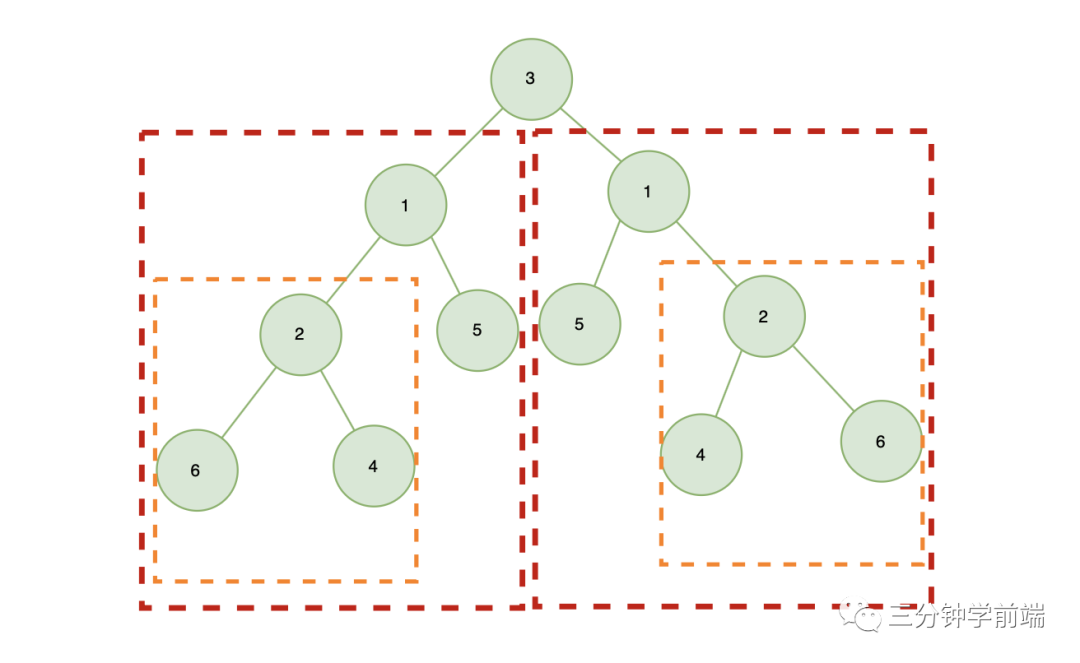
所以,我們需要比較:
-
左右子樹的根節(jié)點(diǎn)值是否相等 -
左右子樹是否鏡像對(duì)稱
邊界條件:
-
左右子樹都為 null時(shí),返回true -
左右子樹有一個(gè) null時(shí),返回false
解法一:遞歸
const isSymmetric = function(root) {
if(!root) return true
var isEqual = function(left, right) {
if(!left && !right) return true
if(!left || !right) return false
return left.val === right.val
&& isEqual(left.left, right.right)
&& isEqual(left.right, right.left)
}
return isEqual(root.left, root.right)
};
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(n)
解法二:迭代
利用棧來記錄比較的過程,實(shí)際上,遞歸就使用了調(diào)用棧,所以這里我們可以使用棧來模擬遞歸的過程
-
首先根的左右子樹入棧 -
將左右子樹出棧,比較兩個(gè)數(shù)是否互為鏡像 -
如果左右子樹的根節(jié)點(diǎn)值相等,則將左子樹的 left、右子樹的right、左子樹的right、右子樹的left依次入棧 -
繼續(xù)出棧(一次出棧兩個(gè)進(jìn)行比較)…….
依次循環(huán)出棧入棧,直到棧為空
const isSymmetric = function(root) {
if(!root) return true
let stack = [root.left, root.right]
while(stack.length) {
let right = stack.pop()
let left = stack.pop()
if(left && right) {
if(left.val !== right.val) return false
stack.push(left.left)
stack.push(right.right)
stack.push(left.right)
stack.push(right.left)
} else if(left || right) {
return false
}
}
return true
};
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(n) -
空間復(fù)雜度:O(n)
劍指Offer&leetcode101:對(duì)稱二叉樹
8.11.11給定一個(gè)二叉樹, 找到該樹中兩個(gè)指定節(jié)點(diǎn)間的最短距離
function TreeNode(val) { this.val = val; this.left = this.right = null; }
解答:
求最近公共祖先節(jié)點(diǎn),然后再求最近公共祖先節(jié)點(diǎn)到兩個(gè)指定節(jié)點(diǎn)的路徑,再求兩個(gè)節(jié)點(diǎn)的路徑之和
const shortestDistance = function(root, p, q) {
// 最近公共祖先
let lowestCA = lowestCommonAncestor(root, p, q)
// 分別求出公共祖先到兩個(gè)節(jié)點(diǎn)的路經(jīng)
let pDis = [], qDis = []
getPath(lowestCA, p, pDis)
getPath(lowestCA, q, qDis)
// 返回路徑之和
return (pDis.length + qDis.length)
}
// 最近公共祖先
const lowestCommonAncestor = function(root, p, q) {
if(root === null || root === p || root === q) return root
const left = lowestCommonAncestor(root.left, p, q)
const right = lowestCommonAncestor(root.right, p, q)
if(left === null) return right
if(right === null) return left
return root
}
const getPath = function(root, p, paths) {
// 找到節(jié)點(diǎn),返回 true
if(root === p) return true
// 當(dāng)前節(jié)點(diǎn)加入路徑中
paths.push(root)
let hasFound = false
// 先找左子樹
if (root.left !== null)
hasFound = getPath(root.left, p, paths)
// 左子樹沒有找到,再找右子樹
if (!hasFound && root.right !== null)
hasFound = getPath(root.right, p, paths)
// 沒有找到,說明不在這個(gè)節(jié)點(diǎn)下面,則彈出
if (!hasFound)
paths.pop()
return hasFound
}
更多解答
8.11.12 二叉搜索樹中第K小的元素
給定一個(gè)二叉搜索樹,編寫一個(gè)函數(shù) kthSmallest 來查找其中第 k 個(gè)最小的元素。
說明:你可以假設(shè) k 總是有效的,1 ≤ k ≤ 二叉搜索樹元素個(gè)數(shù)。
示例 1:
輸入: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
輸出: 1
示例 2:
輸入: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
輸出: 3
進(jìn)階:如果二叉搜索樹經(jīng)常被修改(插入/刪除操作)并且你需要頻繁地查找第 k 小的值,你將如何優(yōu)化 kthSmallest 函數(shù)?
解答:
我們知道:中序遍歷其實(shí)是對(duì)??進(jìn)行排序操作 ,并且是按從小到大的順序排序,所以本題就很簡(jiǎn)單了
解題思路: 中序遍歷二叉搜索樹,輸出第 k 個(gè)既可
代碼實(shí)現(xiàn)(遞歸):
const kthSmallest = function(root, k) {
let res = null
let inOrderTraverseNode = function(node) {
if(node !== null && k > 0) {
// 先遍歷左子樹
inOrderTraverseNode(node.left)
// 然后根節(jié)點(diǎn)
if(--k === 0) {
res = node.val
return
}
// 再遍歷右子樹
inOrderTraverseNode(node.right)
}
}
inOrderTraverseNode(root)
return res
}
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(k) -
空間復(fù)雜度:不考慮遞歸棧所占用的空間,空間復(fù)雜度為 O(1)
代碼實(shí)現(xiàn)(迭代):
const kthSmallest = function(root, k) {
let stack = []
let node = root
while(node || stack.length) {
// 遍歷左子樹
while(node) {
stack.push(node)
node = node.left
}
node = stack.pop()
if(--k === 0) {
return node.val
}
node = node.right
}
return null
}
復(fù)雜度分析:
-
時(shí)間復(fù)雜度:O(H+K) -
空間復(fù)雜度:空間復(fù)雜度為 O(H+K)
更多解答
8.11.13 實(shí)現(xiàn) Trie(前綴樹)
實(shí)現(xiàn)一個(gè) Trie (前綴樹),包含 insert , search , 和 startsWith 這三個(gè)操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true
說明:
-
你可以假設(shè)所有的輸入都是由小寫字母 a-z 構(gòu)成的。 -
保證所有輸入均為非空字符串。
解答:
我們可以搭建一個(gè)初始 Trie 樹結(jié)構(gòu):
// Trie 樹
var Trie = function() {};
// 插入
Trie.prototype.insert = function(word) {};
// 搜索
Trie.prototype.search = function(word) {};
// 前綴匹配
Trie.prototype.startsWith = function(prefix) {};
1. 如何存儲(chǔ)一個(gè) Trie 樹
首先,我們需要實(shí)現(xiàn)一個(gè) Trie 樹,我們知道,二叉樹的存儲(chǔ)(鏈?zhǔn)酱鎯?chǔ))是通過左右指針來實(shí)現(xiàn)的,即二叉樹中的節(jié)點(diǎn):
function BinaryTreeNode(key) {
// 保存當(dāng)前節(jié)點(diǎn) key 值
this.key = key
// 指向左子節(jié)點(diǎn)
this.left = null
// 指向右子節(jié)點(diǎn)
this.right = null
}
在這里,它不止有兩個(gè)字節(jié)點(diǎn),它最多有 a-z 總共有26個(gè)子節(jié)點(diǎn)。最簡(jiǎn)單的實(shí)現(xiàn)是把她們保存在一個(gè)字典里:
-
isEnd:當(dāng)前是否是結(jié)束節(jié)點(diǎn) -
children:當(dāng)前節(jié)點(diǎn)的子節(jié)點(diǎn),這里我們使用key:value形式實(shí)現(xiàn),key為子節(jié)點(diǎn)字符,value指向子節(jié)點(diǎn)的孩子節(jié)點(diǎn)
var TrieNode = function() {
// next 放入當(dāng)前節(jié)點(diǎn)的子節(jié)點(diǎn)
this.next = {};
// 當(dāng)前是否是結(jié)束節(jié)點(diǎn)
this.isEnd = false;
};
所以:
// Trie 樹
var Trie = function() {
this.root = new TrieNode()
};
2. 插入
-
首先判斷插入節(jié)點(diǎn)是否為空,為空則返回 -
遍歷待插入字符,從根節(jié)點(diǎn)逐字符查找 Trie 樹,如果字符查找失敗則插入,否則繼續(xù)查找下一個(gè)字符 -
待插入字符遍歷完成,設(shè)置最后字符的 isEnd為true -
返回插入成功
Trie.prototype.insert = function(word) {
if (!word) return false
let node = this.root
for (let i = 0; i < word.length; i++) {
if (!node.next[word[i]]) {
node.next[word[i]] = new TrieNode()
}
node = node.next[word[i]]
}
node.isEnd = true
return true
};
3. 搜索
Trie.prototype.search = function(word) {
if (!word) return false
let node = this.root
for (let i = 0; i < word.length; ++i) {
if (node.next[word[i]]) {
node = node.next[word[i]]
} else {
return false
}
}
return node.isEnd
};
4. 前綴匹配
Trie.prototype.startsWith = function(prefix) {
if (!prefix) return true
let node = this.root
for (let i = 0; i < prefix.length; ++i) {
if (node.next[prefix[i]]) {
node = node.next[prefix[i]]
} else {
return false
}
}
return true
};最近開源了一個(gè)github倉(cāng)庫:百問百答,在工作中很難做到對(duì)社群?jiǎn)栴}進(jìn)行立即解答,所以可以將問題提交至 https://github.com/Advanced-Frontend/Just-Now-QA ,我會(huì)在每晚花費(fèi) 1 個(gè)小時(shí)左右進(jìn)行處理,更多的是鼓勵(lì)與歡迎更多人一起參與探討與解答??
最后
號(hào)內(nèi)回復(fù):
120 套模版
