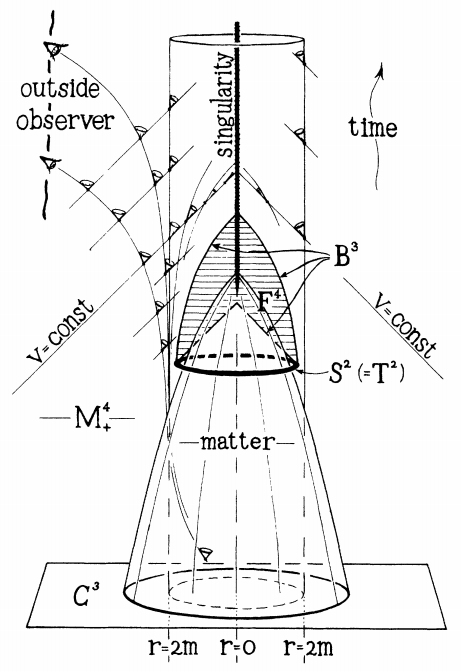
數(shù)學家為啥能研究黑洞,還能拿諾貝爾物理學獎?

不想看公式就直接看留言。說黑洞,不得不說愛因斯坦提出的廣義相對論中的場方程。

愛因斯坦場方程
左側(cè)
: Ricci 曲率張量 : 標量曲率,由 Ricci 曲率張量縮并而來 : 4 維時空的度量張量 : 宇宙學常數(shù)
右側(cè)
: 牛頓的重力常數(shù) : 光速 : 應力-能量張量
曲率張量聽上去是不是很高大上,其實這里指的是 2 階張量,可以直接用一個矩陣表示。只是它們都是物理量,不受坐標系選擇的影響。
愛因斯坦場方程是描述了時空中每一點處能量動量的數(shù)量關系,但是每一點的上面那些張量可以不同。用到的背景工具是黎曼幾何以及張量分析。
我們可以簡單地想象成一張嵌在 3 維空間中的 2 維曲面,然后你在這些面上生活,只是它那里是 4 維的。
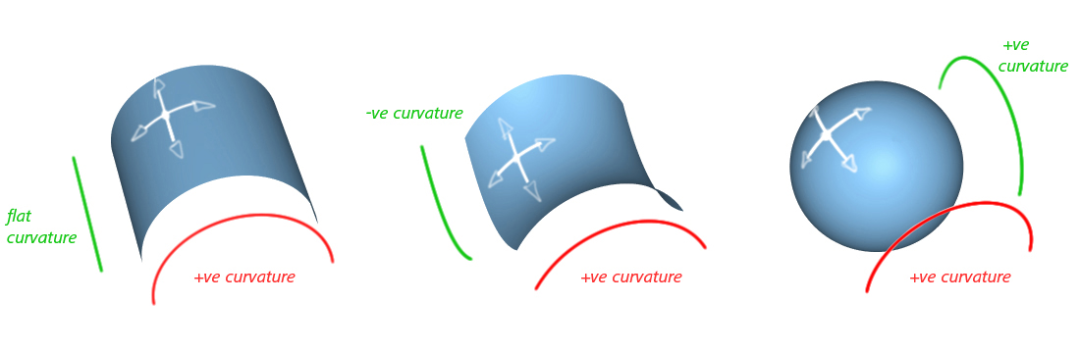
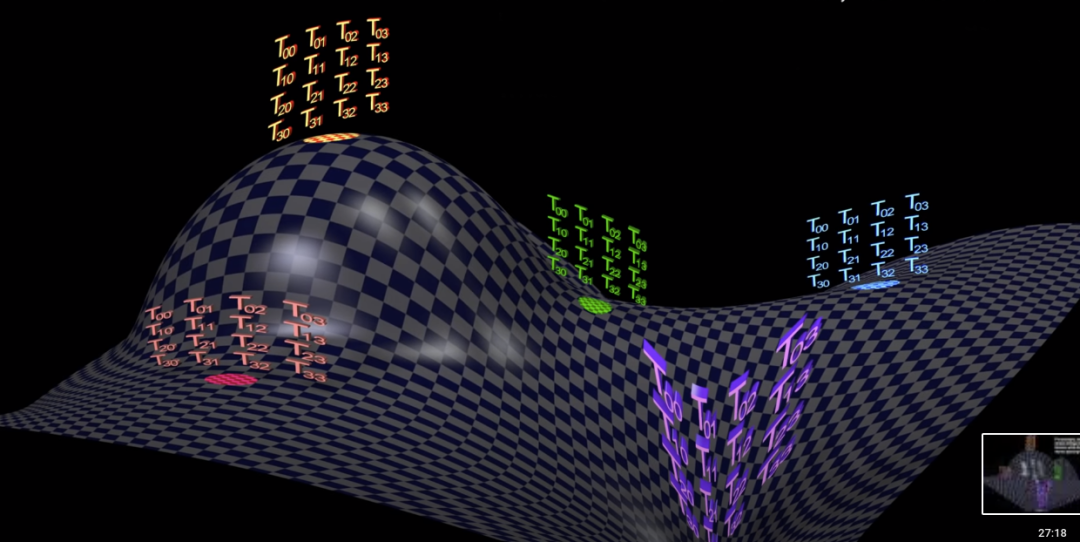
上面那個場方程中的張量在時空中每一點可以不同,相當于在每一點配上了好幾個矩陣,每點的標量 R 其實也類似,這里省略。可以設想宇宙中每點都有好幾把尺子,它們還可以處處不同。
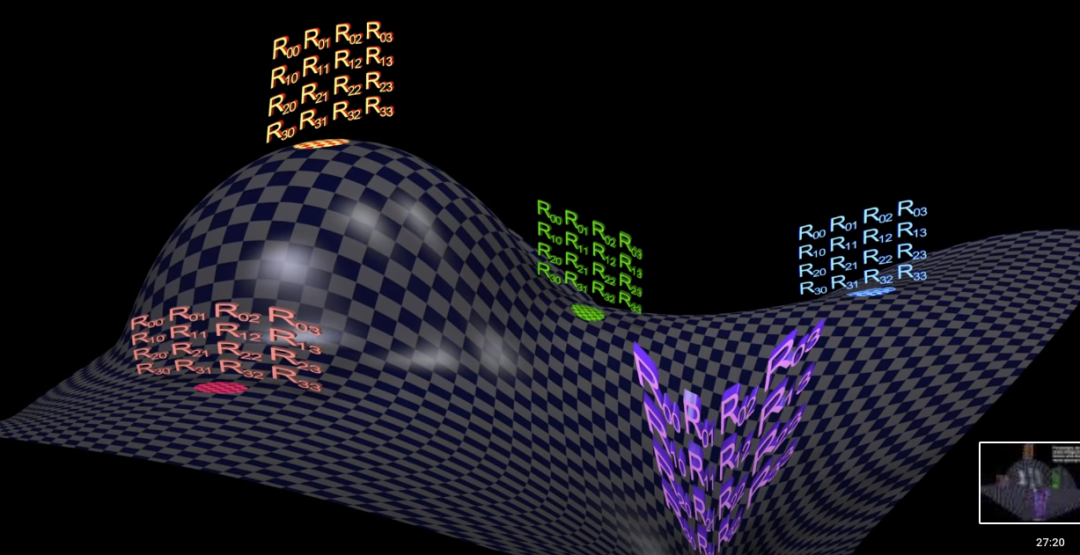
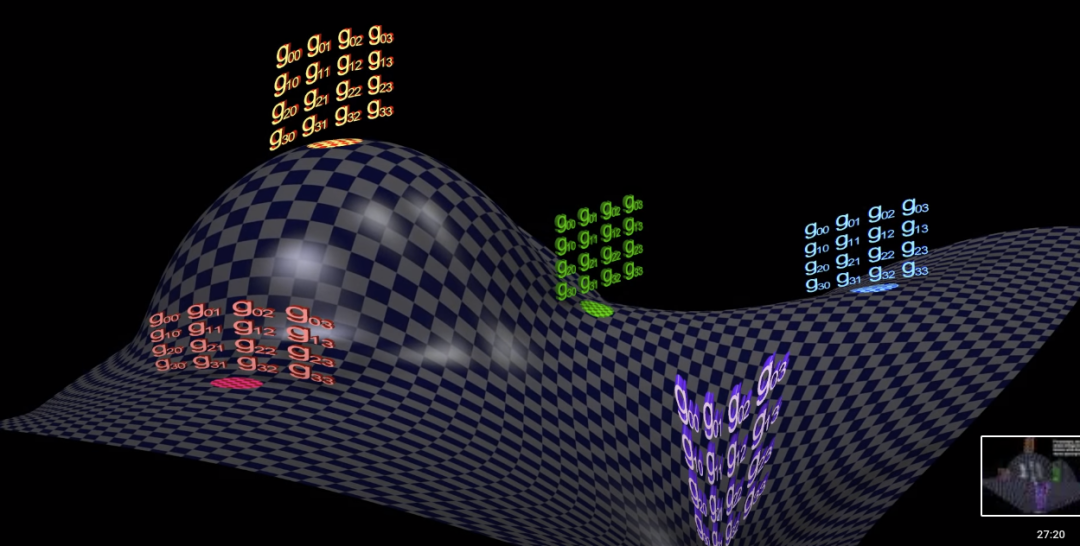
愛因斯坦認為,引力場或者物質(zhì)的存在導致了時空的彎曲,而時空的彎曲恰恰體現(xiàn)了引力本身。上面的場方程就是把愛因斯坦的這個思想給數(shù)量化了。
可是,這個跟黑洞有神馬關系?愛因斯坦在場方程中早就想到黑洞這回事了?
方程的解
這個方程的左邊對應時空彎曲,而右邊對應物質(zhì)及其運動。愛因斯坦拍腦袋(上帝給了他靈感吧),再加上一些數(shù)學家的幫助,他終于搞定了這個方程。
但是,這相當于只是給時空中每一點下了一些規(guī)矩,具體時空是怎么樣的,需要求解這個場方程才知道。解方程也意味著構(gòu)造時空,換句話說,不同的解對應著一個不同的宇宙。那么我們所處的宇宙到底是怎么樣的呢?

第一個從數(shù)學上求解這個方程的是德國天文物理學家卡爾·施瓦西,他得出,
其中,
注意它的分母,
數(shù)學家、物理學家有辦法,給它取個名字特殊化就可以了,對,就叫它奇點。史瓦西認為,奇點附近將具有極大的引力,邊上任何物質(zhì),連光都得被吸進去了。后來美國物理學家惠勒將它命名為黑洞。

那么它存在嗎?仔細看,其中的

史瓦西的解最讓人振奮的一面是,它從數(shù)學上預言了黑洞。注意,是數(shù)學上。那么我們實際的宇宙到底有沒有黑洞呢?拍腦袋是定不下來的,要么就問上帝,要么根據(jù)實際觀測來推斷。
彭羅斯做了什么
這次數(shù)學家彭羅斯得了諾貝爾獎,是因為他從純數(shù)學的角度研究黑洞,并提出了所謂的奇點定理,從而從理論上去除了對解的對稱性要求。
像上面史瓦西等人提出的一些解的存在是嚴重依賴對稱性的,而真實宇宙環(huán)境中的對稱性會不會有那么完美呢?那么依賴這種解的黑洞是不是不存在呢?天體坍縮是否能滿足這個對稱性從而形成黑洞呢?

在彭羅斯之前,天文界的主流觀點認為黑洞多半是意淫出來的,在我們所處的宇宙中估計是不存在。
而彭羅斯在上世紀六十年代,從純數(shù)學的角度來研究天體物理。他在 1965 年的論文(Gravitational Collapse and Space-Time Singularities)中指出,即使偏離球面對稱仍然會出現(xiàn)時空奇點。
也就是說,不管對稱不對稱之類的要求,最終都會出現(xiàn)一個數(shù)學上的奇點,這個奇點就能形成黑洞。從而重新燃起了天文學界對黑洞的熱情,促使人們繼續(xù)去尋找黑洞。