AVL樹的C++實現
首先,AVL 樹是二叉查找樹,即任意一個節(jié)點的左子結點小于當前結點,右子結點大于當前結點。
然后,AVL 樹是平衡樹,任意一個結點的左子樹和右子樹高度差的絕對值小于等于 1。
定義
template <typename T>
class AVLTreeNode {
public:
T key;
int height = 1; //樹高
AVLTreeNode* l;
AVLTreeNode* r;
AVLTreeNode(T _key, AVLTreeNode* _l, AVLTreeNode* _r) : key(_key), l(_l), r(_r) {}
};
template <typename T>
class AVLTree {
public:
AVLTreeNode<T>* root;
AVLTree() { this->root = nullptr; }
~AVLTree();
int height(AVLTreeNode<T>* tree);
int height();
void insert(T key);
void remove(T key);
AVLTreeNode<T>* find(T key);
void print();
private:
AVLTreeNode<T>* LLRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* LRRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* RRRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* RLRotation(AVLTreeNode<T>* k2);
AVLTreeNode<T>* insert(T key, AVLTreeNode<T>* root);
AVLTreeNode<T>* remove(AVLTreeNode<T>* del, AVLTreeNode<T>* root);
AVLTreeNode<T>* find(T key, AVLTreeNode<T>* root);
AVLTreeNode<T>* findmax(AVLTreeNode<T>* root);
AVLTreeNode<T>* findmin(AVLTreeNode<T>* root);
};
旋轉
AVL 樹的旋轉有 4 種,LL,RR,LR,RL。
LL
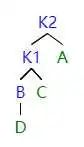
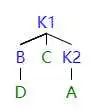
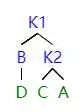
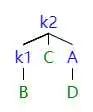
如圖所示,當左子樹的左子樹影響平衡的時候,我們需要進行 LL 旋轉。
首先,我們把 k1 提起來 (就像提繩子一樣),這時候 k1 是根結點。但是這時候會發(fā)現 k1 有三個子節(jié)點,不符合二叉樹的定義。同時又因為 k2 剛好被轉過去,沒有左子結點。所以我們就把 k1 原先的右子樹給 k2 當左子樹。
因為 k2 之前是根節(jié)點,所以 k2>k1 的右子結點 > k1,如上操作之后,符合 AVL 樹的定義。
每次旋轉之后都重新計算樹高。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::LLRotation(AVLTreeNode<T>* k2) {
AVLTreeNode<T>* k1;
k1 = k2->l;
k2->l = k1->r;
k1->r = k2;
k2->height = max(height(k2->l), height(k2->r)) + 1;
k1->height = max(height(k1->l), k2->height) + 1;
return k1;
}
RR
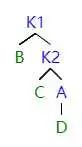
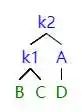
理解 LL 之后,RR 就很好理解。
當右子樹的右子樹影響平衡之后,我們首先把 k2 提起來,現在 k1 缺少右子結點,我們就把 k2 之前的左子樹給過去。
因為 k2>k2 的左子結點 > k1,操作之后符合 AVL 樹的定義。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::RRRotation(AVLTreeNode<T>* k1) {
AVLTreeNode<T>* k2;
k2 = k1->r;
k1->r = k2->l;
k2->l = k1;
k1->height = max(height(k1->l), height(k1->r)) + 1;
k2->height = max(height(k2->r), k1->height) + 1;
return k2;
}
LR
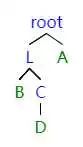
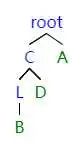
當左子樹的右子樹影響平衡的時候,我們對右子樹進行一次 RR 旋轉,之后就轉化為 LL 旋轉。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::LRRotation(AVLTreeNode<T>* root) {
root->l = RRRotation(root->l);
return LLRotation(root);
}
RL
理解以上幾個之后,RL 也就很好理解了,此處不再贅述,請讀者自行思考。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::RLRotation(AVLTreeNode<T>* root) {
root->r = LLRotation(root->r);
return RRRotation(root);
}
插入
我們遞歸查找插入的位置,回溯的過程中發(fā)現不平衡就去進行旋轉。
template <typename T>
AVLTreeNode<T>* AVLTree<T>::insert(T key, AVLTreeNode<T>* root) {
if (root == nullptr) {
root = new AVLTreeNode<T>(key, nullptr, nullptr);
}
else if (key < root->key) {//插入到左子樹
root->l = insert(key, root->l);
if (height(root->l) - height(root->r) == 2) {
if (key < root->l->key) {
root = LLRotation(root);
}
else {
root = LRRotation(root);
}
}
}
else if (key > root->key) {//插入到右子樹
root->r = insert(key, root->r);
if (height(root->r) - height(root->l) == 2) {
if (key > root->r->key) {
root = RRRotation(root);
}
else {
root = RLRotation(root);
}
}
}
root->height = max(height(root->l), height(root->r)) + 1;
return root;
}
template <typename T>
void AVLTree<T>::insert(T key) {
root = insert(key, root);
}
查找和刪除
template <typename T>
AVLTreeNode<T>* AVLTree<T>::find(T key) {
return find(key, root);
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::find(T key, AVLTreeNode<T>* root) {
if (root == nullptr)
return root;
if (key > root->key) {
return find(key, root->r);
}
else if (key < root->key) {
return find(key, root->l);
}
else
return root;
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::findmax(AVLTreeNode<T>* root) {
if (root->r == nullptr)
return root;
return findmax(root->r);
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::findmin(AVLTreeNode<T>* root) {
if (root->l == nullptr)
return root;
return findmin(root->l);
}
template <typename T>
AVLTreeNode<T>* AVLTree<T>::remove(AVLTreeNode<T>* del, AVLTreeNode<T>* root) {
//沒找到直接返回
if (root == nullptr || del == nullptr)
return root;
if (del->key < root->key) {//需要刪除的結點在左子樹中
root->l = remove(del, root->l);
if (height(root->r) - height(root->l) == 2) {
if (height(root->r->l) > height(root->r->r)) {
root = RLRotation(root);
}
else {
root = RRRotation(root);
}
}
}
else if (del->key > root->key) {//需要刪除的結點在右子樹中
root->r = remove(del, root->r);
if (height(root->l) - height(root->r) == 2) {
if (height(root->l->r) > height(root->l->l)) {
root = LRRotation(root);
}
else {
root = LLRotation(root);
}
}
}
else {
//左右子樹都不為空,刪除后,我們可以用左子樹的最大結點或右子樹的最小結點來替換這個結點
if (root->l != nullptr && root->r != nullptr) {
if (height(root->l) > height(root->r)) {
//用左子樹的最大結點,好處是刪除后還是平衡的,無需旋轉
AVLTreeNode<T>* mx = findmax(root->l);
root->key = mx->key;
root->l = remove(mx, root->l);
}
else {
//用右子樹的最大結點,好處同上
AVLTreeNode<T>* mn = findmin(root->r);
root->key = mn->key;
root->r = remove(mn, root->r);
}
}
else {
AVLTreeNode<T>* tmp = root;
root = (root->l == nullptr) ? root->r : root->l;
delete tmp;
}
}
return root;
}
template <typename T>
void AVLTree<T>::remove(T key) {
root = remove(find(key), root);
}
總結
至于析構,遍歷等等的代碼和此處不再給出,請參照正常的二叉樹操作自行思考。
AVL 樹的實現實際上不難,由于各種教材上冗長的介紹,使得我們有一種認為它難的錯覺。
評論
圖片
表情
