蒙特卡洛樹是什么算法？

點(diǎn)擊上方“小白學(xué)視覺”，選擇加"星標(biāo)"或“置頂”

重磅干貨，第一時(shí)間送達(dá)

編輯：憶臻

https://www.zhihu.com/question/39916945

本文僅作為學(xué)術(shù)分享，如果侵權(quán)，會(huì)刪文處理

?

蒙特卡洛樹是什么算法？

作者：陸君慨
https://www.zhihu.com/question/39916945/answer/83799720

蒙特卡羅樹搜索(Monte Carlo Tree Search)并不是一種"模擬人"的算法。而是通過隨機(jī)的對游戲進(jìn)行推演來逐漸建立一棵不對稱的搜索樹的過程。可以看成是某種意義上的強(qiáng)化學(xué)習(xí)，當(dāng)然這一點(diǎn)學(xué)界還有一些爭議。

蒙特卡羅樹搜索大概可以被分成四步。選擇(Selection)，拓展(Expansion)，模擬(Simulation)，反向傳播(Backpropagation)。

在開始階段，搜索樹只有一個(gè)節(jié)點(diǎn)，也就是我們需要決策的局面。

搜索樹中的每一個(gè)節(jié)點(diǎn)包含了三個(gè)基本信息：代表的局面，被訪問的次數(shù)，累計(jì)評分。

在選擇階段，需要從根節(jié)點(diǎn)，也就是要做決策的局面R出發(fā)向下選擇出一個(gè)最急迫需要被拓展的節(jié)點(diǎn)N，局面R是是每一次迭代中第一個(gè)被檢查的節(jié)點(diǎn)；

對于被檢查的局面而言，他可能有三種可能：

1)該節(jié)點(diǎn)所有可行動(dòng)作都已經(jīng)被拓展過

2)該節(jié)點(diǎn)有可行動(dòng)作還未被拓展過

3)這個(gè)節(jié)點(diǎn)游戲已經(jīng)結(jié)束了(例如已經(jīng)連成五子的五子棋局面)

對于這三種可能：

1)如果所有可行動(dòng)作都已經(jīng)被拓展過了，那么我們將使用UCB公式計(jì)算該節(jié)點(diǎn)所有子節(jié)點(diǎn)的UCB值，并找到值最大的一個(gè)子節(jié)點(diǎn)繼續(xù)檢查。反復(fù)向下迭代。

2)如果被檢查的局面依然存在沒有被拓展的子節(jié)點(diǎn)(例如說某節(jié)點(diǎn)有20個(gè)可行動(dòng)作，但是在搜索樹中才創(chuàng)建了19個(gè)子節(jié)點(diǎn))，那么我們認(rèn)為這個(gè)節(jié)點(diǎn)就是本次迭代的的目標(biāo)節(jié)點(diǎn)N，并找出N還未被拓展的動(dòng)作A。執(zhí)行步驟[2]

3)如果被檢查到的節(jié)點(diǎn)是一個(gè)游戲已經(jīng)結(jié)束的節(jié)點(diǎn)。那么從該節(jié)點(diǎn)直接執(zhí)行步驟{4]。

每一個(gè)被檢查的節(jié)點(diǎn)的被訪問次數(shù)在這個(gè)階段都會(huì)自增。

在反復(fù)的迭代之后，我們將在搜索樹的底端找到一個(gè)節(jié)點(diǎn)，來繼續(xù)后面的步驟。

[2]拓展(Expansion)

在選擇階段結(jié)束時(shí)候，我們查找到了一個(gè)最迫切被拓展的節(jié)點(diǎn)N，以及他一個(gè)尚未拓展的動(dòng)作A。在搜索樹中創(chuàng)建一個(gè)新的節(jié)點(diǎn)Nn作為N的一個(gè)新子節(jié)點(diǎn)。Nn的局面就是節(jié)點(diǎn)N在執(zhí)行了動(dòng)作A之后的局面。

[3]模擬(Simulation)

為了讓Nn得到一個(gè)初始的評分。我們從Nn開始，讓游戲隨機(jī)進(jìn)行，直到得到一個(gè)游戲結(jié)局，這個(gè)結(jié)局將作為Nn的初始評分。一般使用勝利/失敗來作為評分，只有1或者0。

[4]反向傳播(Backpropagation)

在Nn的模擬結(jié)束之后，它的父節(jié)點(diǎn)N以及從根節(jié)點(diǎn)到N的路徑上的所有節(jié)點(diǎn)都會(huì)根據(jù)本次模擬的結(jié)果來添加自己的累計(jì)評分。如果在[1]的選擇中直接發(fā)現(xiàn)了一個(gè)游戲結(jié)局的話，根據(jù)該結(jié)局來更新評分。

每一次迭代都會(huì)拓展搜索樹，隨著迭代次數(shù)的增加，搜索樹的規(guī)模也不斷增加。當(dāng)?shù)搅艘欢ǖ牡螖?shù)或者時(shí)間之后結(jié)束，選擇根節(jié)點(diǎn)下最好的子節(jié)點(diǎn)作為本次決策的結(jié)果。

一次迭代的圖例[1]:

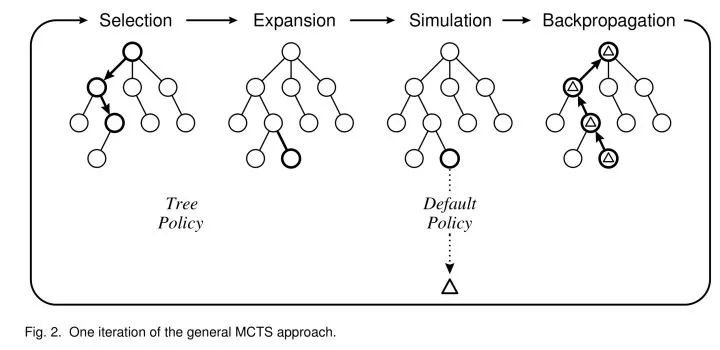
上面描述的是UCT (UCB for Tree)算法，可以說是最經(jīng)典的蒙特卡羅樹搜索算法了。但隨著算法的發(fā)展，MCTS已經(jīng)有了非常大的改變。例如很多圍棋AI都已經(jīng)不再使用純粹的UCB公式而改用效果更好的UCB1-Tuned了[2]，而搜索方法上也有了非常多的改動(dòng)了。

Reference:

[1]:Browne C B, Powley E, Whitehouse D, et al. A Survey of Monte Carlo Tree Search Methods[J]. IEEE Transactions on Computational Intelligence & Ai in Games, 2012, 4:1(1):1-43.

[2]:P. Auer, N. Cesa-Bianchi, and P. Fischer, “Finite-time Analysis ?of the Multiarmed Bandit Problem,” Mach. Learn., vol. 47, no. 2, ?pp. 235–256, 2002.

作者：vczh
https://www.zhihu.com/question/39916945/answer/247549008

傳統(tǒng)意義上講，算法名字帶有蒙特卡洛的意思就是，他對搜索空間的搜索都是隨機(jī)給一個(gè)方向的，譬如說蒙塔卡羅算圓周率，就是在一個(gè)正方形里面隨機(jī)取點(diǎn)，看看落在圓里面有多少。蒙特卡洛光線追蹤，在需要對環(huán)境積分的時(shí)候隨機(jī)取角度射光線。蒙特卡洛走迷宮，隨便走。

作者：Xiaohu Zhu
https://www.zhihu.com/question/39916945/answer/247549008

什么是 MCTS？

全稱 Monte Carlo Tree Search，是一種人工智能問題中做出最優(yōu)決策的方法，一般是在組合博弈中的行動(dòng)（move）規(guī)劃形式。它結(jié)合了隨機(jī)模擬的一般性和樹搜索的準(zhǔn)確性。

MCTS 受到快速關(guān)注主要是由計(jì)算機(jī)圍棋程序的成功以及其潛在的在眾多難題上的應(yīng)用所致。超越博弈游戲本身，MCTS 理論上可以被用在以 {狀態(tài) state，行動(dòng) action} 對定義和用模擬進(jìn)行預(yù)測輸出結(jié)果的任何領(lǐng)域。

基本算法

基本的 MCTS 算法非常簡單：根據(jù)模擬的輸出結(jié)果，按照節(jié)點(diǎn)構(gòu)造搜索樹。其過程可以分為下面的若干步：

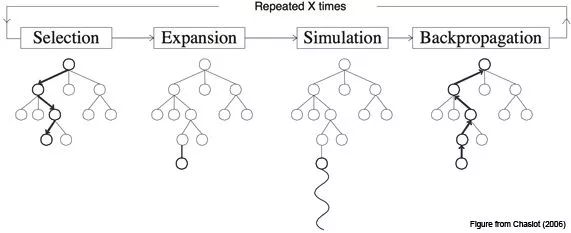
選擇 Selection：從根節(jié)點(diǎn) R 開始，遞歸選擇最優(yōu)的子節(jié)點(diǎn)（后面會(huì)解釋）直到達(dá)到葉子節(jié)點(diǎn) L。

1. 擴(kuò)展 Expansion：如果 L 不是一個(gè)終止節(jié)點(diǎn)（也就是，不會(huì)導(dǎo)致博弈游戲終止）那么就創(chuàng)建一個(gè)或者更多的字子節(jié)點(diǎn)，選擇其中一個(gè) C。

2. 模擬 Simulation：從 C 開始運(yùn)行一個(gè)模擬的輸出，直到博弈游戲結(jié)束。

3. 反向傳播 Backpropagation：用模擬的結(jié)果輸出更新當(dāng)前行動(dòng)序列。

參看Tutorial 了解關(guān)于這個(gè)過程更多的信息。

每個(gè)節(jié)點(diǎn)并需包含兩個(gè)重要的信息：一個(gè)是根據(jù)模擬結(jié)果估計(jì)的值和該節(jié)點(diǎn)已經(jīng)被訪問的次數(shù)。

按照最為簡單和最節(jié)約內(nèi)存的實(shí)現(xiàn)，MCTS 將在每個(gè)迭代過程中增加一個(gè)子節(jié)點(diǎn)。不過，要注意其實(shí)根據(jù)不同的應(yīng)用這里也可以在每個(gè)迭代過程中增加超過一個(gè)子節(jié)點(diǎn)。

?

節(jié)點(diǎn)選擇

Bandits 和 UCB

在樹向下遍歷時(shí)的節(jié)點(diǎn)選擇通過選擇最大化某個(gè)量來實(shí)現(xiàn)，這其實(shí)類似于 Multiarmed bandit problem，其中的參與者必須選擇一個(gè) slot machine（bandit）來最大化每一輪的估計(jì)的收益。我們可以使用 Upper Confidence Bounds（UCB）公式常常被用來計(jì)算這個(gè)：

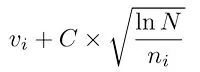
其中 v_i 是節(jié)點(diǎn)估計(jì)的值，n_i 是節(jié)點(diǎn)被訪問的次數(shù)，而 N 則是其父節(jié)點(diǎn)已經(jīng)被訪問的總次數(shù)。C 是可調(diào)整參數(shù)。

Exploitation 和 Exploration

UCB 公式對已知收益的 exploitation 和鼓勵(lì)接觸那些相對未曾訪問的節(jié)點(diǎn)的 exploration 進(jìn)行平衡。收益估計(jì)基于隨機(jī)模擬，所以節(jié)點(diǎn)必須被訪問若干次來缺包估計(jì)變得更加可信；MCTS 估計(jì)會(huì)在搜索的開始不大可靠，而最終會(huì)在給定充分的時(shí)間后收斂到更加可靠的估計(jì)上，在無限時(shí)間下能夠達(dá)到最優(yōu)估計(jì)。

MCTS 和 UCT

Kocsis 和 Szepervari 在 2006 年首先構(gòu)建了一個(gè)完備的 MCTS 算法，通過擴(kuò)展 UCB 到 minimax 樹搜索，并將其命名為 Upper Confidence Bounds for Trees（UCT）方法。這其實(shí)是用在當(dāng)前眾多 MCTS 實(shí)現(xiàn)中的算法版本。

UCT 可以被描述為 MCTS 的一個(gè)特例：UCT = MCTS + UCB。

優(yōu)點(diǎn)

MCTS 提供了比傳統(tǒng)樹搜索更好的方法。

Aheuristic

MCTS 不要求任何關(guān)于給定的領(lǐng)域策略或者具體實(shí)踐知識(shí)來做出合理的決策。這個(gè)算法可以在沒有任何關(guān)于博弈游戲除基本規(guī)則外的知識(shí)的情況下進(jìn)行有效工作；這意味著一個(gè)簡單的 MCTS 實(shí)現(xiàn)可以重用在很多的博弈游戲中，只需要進(jìn)行微小的調(diào)整，所以這也使得 MCTS 是對于一般的博弈游戲的很好的方法。

Asymmetric

MCTS 執(zhí)行一種非對稱的樹的適應(yīng)搜索空間拓?fù)浣Y(jié)構(gòu)的增長。這個(gè)算法會(huì)更頻繁地訪問更加有趣的節(jié)點(diǎn)，并聚焦其搜索時(shí)間在更加相關(guān)的樹的部分。

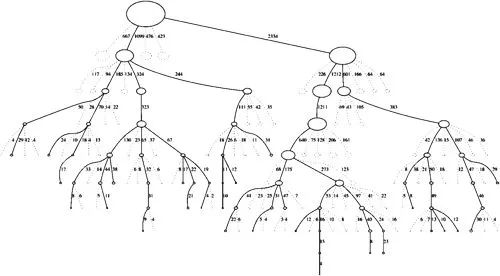
這使得 MCTS 更加適合那些有著更大的分支因子的博弈游戲，比如說 19X19 的圍棋。這么大的組合空間會(huì)給標(biāo)準(zhǔn)的基于深度或者寬度的搜索方法帶來問題，所以 MCTS 的適應(yīng)性說明它（最終）可以找到那些更加優(yōu)化的行動(dòng)，并將搜索的工作聚焦在這些部分。

任何時(shí)間算法可以在任何時(shí)間終止，并返回當(dāng)前最有的估計(jì)。當(dāng)前構(gòu)造出來的搜索樹可以被丟棄或者供后續(xù)重用。簡潔算法實(shí)現(xiàn)非常方便

缺點(diǎn)

MCTS 有很少的缺點(diǎn)，不過這些缺點(diǎn)也可能是非常關(guān)鍵的影響因素。

行為能力

MCTS 算法，根據(jù)其基本形式，在某些甚至不是很大的博弈游戲中在可承受的時(shí)間內(nèi)也不能夠找到最好的行動(dòng)方式。這基本上是由于組合步的空間的全部大小所致，關(guān)鍵節(jié)點(diǎn)并不能夠訪問足夠多的次數(shù)來給出合理的估計(jì)。

速度

MCTS 搜索可能需要足夠多的迭代才能收斂到一個(gè)很好的解上，這也是更加一般的難以優(yōu)化的應(yīng)用上的問題。例如，最佳的圍棋程序可能需要百萬次的交戰(zhàn)和領(lǐng)域最佳和強(qiáng)化才能得到專家級(jí)的行動(dòng)方案，而最有的 GGP 實(shí)現(xiàn)對更加復(fù)雜的博弈游戲可能也就只要每秒鐘數(shù)十次（領(lǐng)域無關(guān)的）交戰(zhàn)。對可承受的行動(dòng)時(shí)間，這樣的 GGP 可能很少有時(shí)間訪問到每個(gè)合理的行動(dòng)，所以這樣的情形也不大可能出現(xiàn)表現(xiàn)非常好的搜索。

幸運(yùn)的是，算法的性能可以通過一些技術(shù)顯著提升。

提升

很多種 MCTS 強(qiáng)化的技術(shù)已經(jīng)出現(xiàn)了。這些基本上可以歸納為領(lǐng)域知識(shí)或者領(lǐng)域獨(dú)立兩大類。

領(lǐng)域知識(shí)

特定博弈游戲的領(lǐng)域知識(shí)可以用在樹上來過濾掉不合理的行動(dòng)或者在模擬過程中產(chǎn)生重要的對局（更接近人類對手的表現(xiàn)）。這意味著交戰(zhàn)結(jié)果將會(huì)更加的現(xiàn)實(shí)而不是隨機(jī)的模擬，所以節(jié)點(diǎn)只需要少量的迭代就能給出一個(gè)現(xiàn)實(shí)的收益值。

領(lǐng)域知識(shí)可以產(chǎn)生巨大的性能提升，但在速度和一般性上也會(huì)有一定的損失。

領(lǐng)域獨(dú)立

領(lǐng)域獨(dú)立強(qiáng)化能夠應(yīng)用到所有的問題領(lǐng)域中。這些一般用在樹種（如 AMAF），還有一些用在模擬（如 在交戰(zhàn)時(shí)傾向于勝利的行動(dòng)）。領(lǐng)域獨(dú)立強(qiáng)化并不和特定的領(lǐng)域綁定，具有一般性，這也是當(dāng)前研究的重心所在。

背景和歷史

1928：John von Neumann 的 minimax 定理給出了關(guān)于對手樹搜索的方法，這形成了計(jì)算機(jī)科學(xué)和人工智能的從誕生至今的決策制定基礎(chǔ)。
1940s：Monte Carlo 方法形成，作為一種通過隨機(jī)采樣解決不太適合樹搜索解決的弱良定義問題的方法。
2006：Rémi Coulomb 和其他研究者組合了上面兩種想法給出了一個(gè)新的圍棋程序中行動(dòng)規(guī)劃的觀點(diǎn)——MCTS。Kocsis 和 Szepesvári 將此觀點(diǎn)形式化進(jìn) UCT 算法。

研究興趣

從 MCTS 誕生后幾年內(nèi)，就有超過 150 篇與 MCTS 相關(guān)的研究論文發(fā)布，平均下來是每兩周一篇新的文章。這些文章中包含了大概 50 個(gè)推薦的變體、強(qiáng)化和優(yōu)化，這和傳統(tǒng)樹搜索自其 1928 年誕生開始的加強(qiáng)的數(shù)量也差不太多。

這個(gè)新的研究領(lǐng)域當(dāng)前是 AI 中非常熱的研究話題，有很多的開放的研究問題有待發(fā)掘和解決。

下載1：OpenCV-Contrib擴(kuò)展模塊中文版教程
在「小白學(xué)視覺」公眾號(hào)后臺(tái)回復(fù)：擴(kuò)展模塊中文教程，即可下載全網(wǎng)第一份OpenCV擴(kuò)展模塊教程中文版，涵蓋擴(kuò)展模塊安裝、SFM算法、立體視覺、目標(biāo)跟蹤、生物視覺、超分辨率處理等二十多章內(nèi)容。

下載2：Python視覺實(shí)戰(zhàn)項(xiàng)目52講
在「小白學(xué)視覺」公眾號(hào)后臺(tái)回復(fù)：Python視覺實(shí)戰(zhàn)項(xiàng)目，即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計(jì)數(shù)、添加眼線、車牌識(shí)別、字符識(shí)別、情緒檢測、文本內(nèi)容提取、面部識(shí)別等31個(gè)視覺實(shí)戰(zhàn)項(xiàng)目，助力快速學(xué)校計(jì)算機(jī)視覺。

下載3：OpenCV實(shí)戰(zhàn)項(xiàng)目20講
在「小白學(xué)視覺」公眾號(hào)后臺(tái)回復(fù)：OpenCV實(shí)戰(zhàn)項(xiàng)目20講，即可下載含有20個(gè)基于OpenCV實(shí)現(xiàn)20個(gè)實(shí)戰(zhàn)項(xiàng)目，實(shí)現(xiàn)OpenCV學(xué)習(xí)進(jìn)階。

交流群

歡迎加入公眾號(hào)讀者群一起和同行交流，目前有SLAM、三維視覺、傳感器、自動(dòng)駕駛、計(jì)算攝影、檢測、分割、識(shí)別、醫(yī)學(xué)影像、GAN、算法競賽等微信群（以后會(huì)逐漸細(xì)分），請掃描下面微信號(hào)加群，備注：”昵稱+學(xué)校/公司+研究方向“，例如：”張三?+?上海交大?+?視覺SLAM“。請按照格式備注，否則不予通過。添加成功后會(huì)根據(jù)研究方向邀請進(jìn)入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告，否則會(huì)請出群，謝謝理解~