來自公眾號(hào):AI科技大本營(yíng)
作者:Your DevOps Guy
翻譯:火火醬~,責(zé)編:晉兆
什么是動(dòng)態(tài)規(guī)劃?它又有什么重要的呢?
在本文中,我將介紹由Richard Bellman在20世紀(jì)50年代提出的動(dòng)態(tài)規(guī)劃(dynamic programming)概念,這是一種強(qiáng)大的算法設(shè)計(jì)技術(shù)——將問題分解成多個(gè)小問題,存儲(chǔ)它們的解,通過將其結(jié)合在一起,最終得到原始問題的解決方案。FAANG編程面試中最難的問題通常都屬于這一類。你在面試的過程中也很可能會(huì)被要求解決這樣的問題,因此,了解這項(xiàng)技術(shù)的重要性自然不言而喻。接下來,我將解釋什么是動(dòng)態(tài)規(guī)劃,給出一個(gè)解決動(dòng)態(tài)規(guī)劃問題的秘訣,并且和大家一起分析幾個(gè)示例,以便你能夠更好地理解其應(yīng)用場(chǎng)合和應(yīng)用方法。和我以往有關(guān)編程面試的文章一樣,在本文中,我將分享自己在使用這種方法解決問題時(shí)的思考過程,這樣當(dāng)你在面對(duì)其中一個(gè)問題時(shí),按照這個(gè)過程一定也能解決。不需要死記硬背,我們只需要通過了解技術(shù)和實(shí)踐,將想法轉(zhuǎn)化成代碼技能。編程的重點(diǎn)不在于學(xué)習(xí)編程語言,而在于分析問題,考慮不同的解決方案,從中選出最優(yōu)解,然后通過某種編程語言將其轉(zhuǎn)化為現(xiàn)實(shí)。 動(dòng)態(tài)規(guī)劃
動(dòng)態(tài)規(guī)劃
動(dòng)態(tài)規(guī)劃是一種解決最優(yōu)化、搜索和計(jì)數(shù)問題的通用技術(shù),這些問題都可以被分解為多個(gè)子問題。要應(yīng)用動(dòng)態(tài)規(guī)劃,問題就必須具備以下兩個(gè)屬性:- 最優(yōu)子結(jié)構(gòu)(Optimal substructure)
- 重疊子問題(Overlapping subproblems)
如果大小為n的問題的最優(yōu)解可以由大小小于n的問題的同一實(shí)例的最優(yōu)解推導(dǎo)出,則該問題具有最優(yōu)子結(jié)構(gòu)。例如,如果從巴黎到莫斯科的最短路徑會(huì)經(jīng)過柏林,那么可以由巴黎到柏林的最短路徑和柏林到莫斯科的最短路徑組成。如果一個(gè)問題可以通過組合非重疊子問題的最優(yōu)解來解決,這種策略被稱為分治法。這就是歸并排序和快速排序不屬于動(dòng)態(tài)規(guī)劃問題的原因。舉一個(gè)大家都很熟悉的例子,斐波那契數(shù)列,即從第三項(xiàng)開始,每一項(xiàng)都等于前兩項(xiàng)之和。斐波那契數(shù)列可以表示為F(0)?=?F(1)?=?1
F(n)?=?F(n-1)?+?F(n-2)
大家都說一張圖片勝過千言萬語,所以......(摘自《Elements of programming interviews》)
? ? ? ?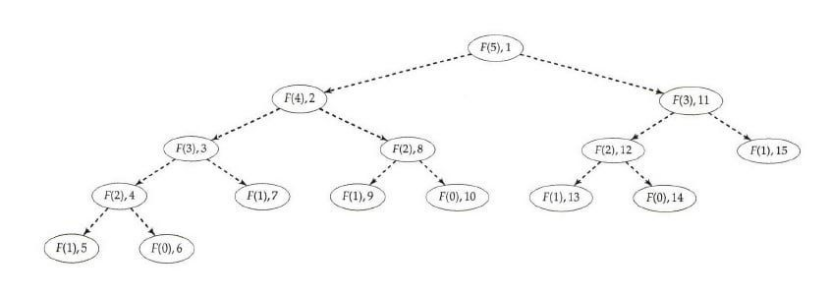 ? ? ?要想解出F(n),就需要解出F(n-1)和F(n-2),但是F(n-1)又需要F(n-2)和F(n-3)。這樣一來,F(xiàn)(n-2)是重復(fù)的,來自于同一個(gè)問題的兩個(gè)不同實(shí)例——計(jì)算一個(gè)斐波那契數(shù)。
? ? ?要想解出F(n),就需要解出F(n-1)和F(n-2),但是F(n-1)又需要F(n-2)和F(n-3)。這樣一來,F(xiàn)(n-2)是重復(fù)的,來自于同一個(gè)問題的兩個(gè)不同實(shí)例——計(jì)算一個(gè)斐波那契數(shù)。- 要想解決一個(gè)大小為n的問題,我們可以調(diào)用相同的函數(shù)來解決同一問題的一個(gè)實(shí)例,但實(shí)例規(guī)模比原始問題規(guī)模小一些。
- 我們一直不斷地調(diào)用該函數(shù),直到到達(dá)基礎(chǔ)用例,也就是停止條件,在此處即n = 0或n = 1。
這就引出了遞歸和動(dòng)態(tài)規(guī)劃之間的關(guān)系。 遞歸和動(dòng)態(tài)規(guī)劃
遞歸和動(dòng)態(tài)規(guī)劃
從概念上講,動(dòng)態(tài)規(guī)劃涉及到遞歸問題。我們希望通過同一個(gè)問題的較小實(shí)例來解決原始問題,而遞歸是在代碼中實(shí)現(xiàn)這一點(diǎn)的最佳選擇。與純遞歸函數(shù)的不同之處在于,我們將用空間來換取時(shí)間:我們將存儲(chǔ)各子問題的最優(yōu)解,進(jìn)而高效地找到原始問題的最優(yōu)解。當(dāng)然,這并不是說我們都必須使用遞歸來解決動(dòng)態(tài)規(guī)劃問題。還可以通過一種迭代方法來編寫動(dòng)態(tài)規(guī)劃解決方案。自下而上的動(dòng)態(tài)規(guī)劃我們需要將所有子問題的解決方案填入表格(從基本用例開始),并用它來構(gòu)建我們正在尋找的解決方案。這個(gè)過程是通過迭代的方式完成的,你可以從下面列別中任選其一作為存儲(chǔ)子問題解決方案的數(shù)據(jù)結(jié)構(gòu):自上而下的動(dòng)態(tài)規(guī)劃編寫遞歸算法并添加緩存層,以避免重復(fù)的函數(shù)調(diào)用。或許現(xiàn)在看起來有點(diǎn)糊涂,但等一會(huì)兒講到示例后,一切都會(huì)清楚得多。 如何解決動(dòng)態(tài)規(guī)劃問題
如何解決動(dòng)態(tài)規(guī)劃問題
如果一個(gè)問題想要通過動(dòng)態(tài)規(guī)劃來解決的話,就必須具備最優(yōu)子結(jié)構(gòu)和重疊子問題這兩個(gè)屬性。當(dāng)直覺告訴你動(dòng)態(tài)規(guī)劃或許是一個(gè)可行的解決方案時(shí),你需要驗(yàn)證其是否具備這兩個(gè)屬性。下面讓我們?cè)囍惺芤幌拢裁礃拥膯栴}可以用動(dòng)態(tài)規(guī)劃來解決。一切以“找到”開頭的問題:解決動(dòng)態(tài)規(guī)劃問題的步驟很不幸,解決動(dòng)態(tài)規(guī)劃問題并沒有什么通用秘訣。我們需要在經(jīng)歷過很多問題之后,才能逐漸掌握其訣竅。這確實(shí)不容易,畢竟這可能會(huì)是你在面試中遇到的最難的問題了。但也先不要?dú)怵H,簡(jiǎn)單來講,就是用相對(duì)簡(jiǎn)單的工具針對(duì)問題進(jìn)行建模,并不需要花哨的數(shù)據(jù)結(jié)構(gòu)或算法。我已經(jīng)解決過很多此類問題了,但有時(shí)還是會(huì)覺得毫無頭緒,找不到解決方法。練習(xí)得越多,就越容易。以下這幾點(diǎn)或許能帶你走近解決動(dòng)態(tài)規(guī)劃問題的秘訣:- 證明重疊子問題和次優(yōu)結(jié)構(gòu)特性。
- 編寫自上而下或自下而上的動(dòng)態(tài)規(guī)劃解決方案。
復(fù)雜度分析因問題而異,但一般來說,時(shí)間復(fù)雜度可以表示為: 時(shí)間~子問題個(gè)數(shù)*每個(gè)子問題的時(shí)間
計(jì)算自下而上解決方案的空間復(fù)雜度很簡(jiǎn)單,因?yàn)槠涞扔诖鎯?chǔ)子問題解決方案所需的空間(多維數(shù)組)。 示例
示例
我已經(jīng)根據(jù)所涉及的獨(dú)立維度的數(shù)量對(duì)問題進(jìn)行了分類。這一步并不是必須的,但我發(fā)現(xiàn)在設(shè)計(jì)解決方案時(shí),遵循一定的心理模型是非常有用的。隨著編寫的代碼越來越多,你會(huì)找到一些模式,而這就是其中之一。不妨試一下,如果覺得有用的話就用起來吧。因?yàn)楝F(xiàn)在大家都已經(jīng)對(duì)這個(gè)問題非常熟悉了,所以我就直接給出遞歸解決方案:int?fib(int?n)?{
??if?(n?==?0?||?n?==?1)
????return?1;
??else
????return?fib(n?-?1)?+?fib(n?-?2);
??}
}
- 檢查我們需要的值是否已經(jīng)在緩存中了。如果是,就返回它。
int?fib(int?n)?{
??vector<int>?cache(n?+?1,?-1);
??return?fib_helper(n,?cache);
}
int?fib_helper(int?n,?vector<int>?&cache)?{
???if(-1?!=?cache[n])
?????return?cache[n];
???if?(n?==?0?||?n?==?1)
?????cache[n]?=?1;
??else
????cache[n]?=?fib_helper(n?-?1,?cache)?+?fib_helper(n?-?2,?cache);
??return?cache[n];
}
這里,用到自下而上的解決方案,我們通過構(gòu)建一個(gè)表(從基本用例為起點(diǎn)),來形成要找的問題的解決方案。這個(gè)表是一個(gè)一維數(shù)組:我們只需要存儲(chǔ)較小的問題的解,就可以推導(dǎo)出原始問題的解。int?fib(int?n)?{
????vector<int>?f(n?+?1,?0);??
????f[1]?=?1;
????for(int?i?=?2;?i?<=?n;?i++)
???????f[i]?=?f[i?-?1]?+?f[i?-?2];
????return?f[n];
}
這種方法可以進(jìn)一步優(yōu)化內(nèi)存,但并不會(huì)優(yōu)化時(shí)間(也可以通過其他技術(shù)更快地計(jì)算斐波納契數(shù)列,但這就是另一篇文章的內(nèi)容了),只需要使用3個(gè)變量,而不必使用數(shù)組,因?yàn)槲覀冎恍枰檭蓚€(gè)值,即f (n - 1)和f (n - 2),就可以得到我們想要的輸出——f (n)。int?fib(int?n)?{??
????if?(n?==?0?||?n?==?1)
??????return?1;
????//Variables?that?represent?f(n?-?1),?f(n?-?2)?and?f(n)
????int?n1=?1,?n2?=?1,?f?=?0;
????for?(int?i?=?2;?i?<=?n;?i++)?{
????????f=?n1?+?n2;
????????n2?=?n1;
????????n1?=?f;
????}
????return?f;
}
這種方法更高級(jí),也更常見。如果只需要跟蹤:- 幾個(gè)變量,或許我們就可以擺脫一維數(shù)組,將其變成幾個(gè)變量。
- 二維矩陣中的幾行,或許我們可以將其減少成幾個(gè)一維數(shù)組。
通過降維,我們提高了空間的復(fù)雜度。現(xiàn)在,你不必記住所有的細(xì)節(jié),但在進(jìn)行過一些實(shí)踐之后,要試著自己提出這些優(yōu)化方案,從而增強(qiáng)自己分析問題并將想法轉(zhuǎn)化為代碼的能力。在面試中,我會(huì)選擇更簡(jiǎn)單的版本,只討論潛在的優(yōu)化方案。只有在編寫了自己的“標(biāo)準(zhǔn)化”動(dòng)態(tài)規(guī)劃解決方案,并且時(shí)間充足的時(shí)候,才動(dòng)手實(shí)施這些優(yōu)化。假設(shè)你正在爬一段有n個(gè)臺(tái)階的樓梯,每次可以爬1或2個(gè)臺(tái)階。那么要想爬到頂端的話,一共有多少種不同的方法呢?- 說明:有三種方法可以爬到頂端:1階+ 1階+ 1階,1階+ 2階,2階+ 1階
先試著自己解決一下這個(gè)問題。你可能會(huì)想到一個(gè)遞歸解決方案。回顧一下我的說明和前面的示例,看看是否可以自行編寫出自上而下的的解決方案。提示一下:既然這個(gè)問題以“有多少種方式”開頭,那就應(yīng)該能想到采用動(dòng)態(tài)規(guī)劃的潛在可能性。在這種情況下,如果想要到達(dá)第N階,就要經(jīng)過第N-1階或第N-2階,因?yàn)橐淮慰梢耘?階或2階。如果我們能解決這兩個(gè)子問題的話,就可以找到一般問題的解。我們將f(N)稱為到第N階的方法數(shù)。- 要得到f(N),就要先求出f(N-1)和 f(N-2)。
- 要得到f(N-1),就要先求出f(N-2)和 f(N-3)。
- 要得到f(N-2),就要先求出f(N-3)和 f(N-4)。
不需要繼續(xù)羅列下去了吧,你應(yīng)該已經(jīng)發(fā)現(xiàn)了:- 這個(gè)問題有重疊的子問題:你需要多次計(jì)算f(N-2), f(N-3), f(N-4),... ...
- 這個(gè)問題向我們展現(xiàn)了最優(yōu)子結(jié)構(gòu):通過f(N-1)和f(N-2)的最優(yōu)解,可以得到f(N)的最優(yōu)解。
這表示我們可以通過動(dòng)態(tài)規(guī)劃來求解該問題。因?yàn)槲乙呀?jīng)在上一個(gè)例子中寫過代碼了,所以這里就不再寫代碼了。大家可以在下方鏈接中試著編寫并測(cè)試一下自己的解決方案。(鏈接地址:https://leetcode.com/problems/climbing-stairs/?ref=hackernoon.com)給定一個(gè)未排序的整數(shù)數(shù)組,求最長(zhǎng)遞增子序列的長(zhǎng)度。例如,對(duì)于數(shù)組[10,9,2,5,3,7,101,18]而言,其輸出為4,即序列[2,3,7,101]我們需要找到大小為n的數(shù)組的最長(zhǎng)遞增子序列的長(zhǎng)度。這聽起來像是一個(gè)可以通過動(dòng)態(tài)規(guī)劃來解決的優(yōu)化問題,那么讓我們來試一下。假設(shè)我們已經(jīng)有了大小為N的問題的解,稱其為s(n),然后我們?cè)跀?shù)組中增加了一個(gè)額外元素,稱為Y。那么,你能重復(fù)使用X的解決方案來解決這個(gè)新問題么?這個(gè)問題通常會(huì)為我們帶來一些啟發(fā)。在這里,我們需要知道新元素是否可以擴(kuò)展任一現(xiàn)有序列:- 迭代數(shù)組中的每一個(gè)元素,我們稱其為X。
- 如果新元素Y大于X,那么序列可以擴(kuò)展一個(gè)元素。
- 如果我們已經(jīng)存儲(chǔ)了所有子問題的解,那么獲取新長(zhǎng)度是非常簡(jiǎn)單的——只需在數(shù)組中進(jìn)行查找即可。我們可以根據(jù)子問題的最優(yōu)解得出新問題的解。
- 返回新的最長(zhǎng)遞增子序列的長(zhǎng)度。
- 最優(yōu)子結(jié)構(gòu):我們已經(jīng)證明了大小為n的問題的最優(yōu)解可以由子問題的最優(yōu)解計(jì)算出來。
- 重疊子問題:要想計(jì)算s(n),則需要s(0), s(1),... ...,s(n-1)。同樣,要計(jì)算s(n-1),則需要s(0), s(1),... ...,s(n-2)。同樣的問題需要進(jìn)行多次計(jì)算。
int?lengthOfLIS(const?vector<int>&?nums)?{
if(nums.empty())
return?0;
vector<int>?dp(nums.size(),?1);
int?maxSol?=?1;
for(int?i?=?0;?i?for(int?j?=?0;?j?if(nums[i]?>?nums[j]){
dp[i]?=?max(dp[i],?dp[j]?+?1);
}
}
maxSol?=?max(maxSol,?dp[i]);
}
return?maxSol;???
}
大家可以在下方鏈接中試著編寫并測(cè)試一下自己的解決方案。
(鏈接地址:https://leetcode.com/problems/longest-increasing-subsequence/?ref=hackernoon.com)對(duì)于給定的n,有多少結(jié)構(gòu)唯一的存儲(chǔ)值為1... ...n的BST(二叉搜索樹)?- 說明:給定n = 5, 總共有42個(gè)唯一的BST
我們一起來看看這個(gè)例子。假設(shè)我們有數(shù)字1、2、3、4、5,如何定義BST?我只需要選擇其中一個(gè)數(shù)作為根,先假設(shè)其為數(shù)字3,則:我們可以解決(1,2)和(4,5)的相同子問題(暫且稱其為解決方案L和R),數(shù)一數(shù)以3為根可以形成多少個(gè)BST,即L*R。如果我們對(duì)每一個(gè)可能的根都這樣做,并且把所有的結(jié)果相加的話,就可以得到我們所需的解決方案C(n)。如你所見,有條不紊地從幾個(gè)例子出發(fā),可以幫助我們更好地設(shè)計(jì)算法。- 解決(1到根-1)和(根+1到n)兩個(gè)數(shù)字的相同問題;
- 將每個(gè)子問題的兩個(gè)結(jié)果相乘;
實(shí)際上,我們并不關(guān)心數(shù)組兩邊的數(shù)字是什么。我們只需要子樹的大小,即根的左右兩邊的元素個(gè)數(shù)。這個(gè)問題中的每個(gè)實(shí)例都會(huì)產(chǎn)生相同的結(jié)果。在之前的例子中,L和R都是C(2)的解。我們只需要計(jì)算一次C(2),緩存,然后重復(fù)使用即可。int?numTrees(int?n)?{
vector<int>?dp(n?+?1,?0);
dp[0]?=?1;
dp[1]?=?1;
for(int?i?=?2;?i?<=?n;?++i){
for(int?j?=?0;?j?dp[i]?+=?dp[j]?*?dp[i?-?1?-?j];
}
}
return?dp.back();
}
大家可以在下方鏈接中試著編寫并測(cè)試一下自己的解決方案。
(鏈接地址:https://leetcode.com/problems/unique-binary-search-trees/?ref=hackernoon.com)這些問題通常比較難建模,因?yàn)樗婕皟蓚€(gè)維度。常見的例子是,在兩個(gè)字符串中迭代,或移動(dòng)映射。- 自上而下的解決方案和之前沒有太大的區(qū)別:找到遞歸并使用緩存。
- 對(duì)于自下而上的解決方案,一個(gè)2D數(shù)組就足以存儲(chǔ)結(jié)果了。像我之前提到的,可能會(huì)減少一個(gè)或幾個(gè)一維數(shù)組,但是沒有必要太在意。之所以提到這一點(diǎn)只是以防你在解決問題時(shí)看到會(huì)有點(diǎn)摸不著頭腦。
我曾在另一篇文章中說過,學(xué)習(xí)是迭代的。首先,要把注意力集中在理解基礎(chǔ)知識(shí)上,然后再一點(diǎn)一點(diǎn)地增加更多的細(xì)節(jié)。給定m×n的非負(fù)數(shù)網(wǎng)格,找出一條從左上到右下的路徑,使路徑上所有數(shù)字之和最小。注意:你只能選擇向下移動(dòng)或向右移動(dòng)。- 輸入:[ [1,3,1], [1,5,1], [4,2,1] ]
最小化問題應(yīng)該會(huì)讓你想到動(dòng)態(tài)規(guī)劃。進(jìn)一步分析,路徑可以經(jīng)過任意單元格C(i,j)(即不在上邊框或左邊框),單元格A = (i-1, j)和B=(i,j-1)。由此,我們發(fā)現(xiàn),有些問題需要進(jìn)行多次計(jì)算。此外,我們?nèi)绻繟和B的最優(yōu)解,就可以計(jì)算出當(dāng)前單元格的最優(yōu)解為min(sol (A),sol(B)) + 1,因?yàn)槲覀冎荒芡ㄟ^當(dāng)前單元格來表示A或B,要想移動(dòng)到當(dāng)前單元格就需要多走一步。換句話說,這是一個(gè)最優(yōu)子結(jié)構(gòu)和重疊問題。我們可以使用動(dòng)態(tài)規(guī)劃。int?minPathSum(const?vector<vector<int>>&?grid)?{
const?int?nrow?=?grid.size();
if(nrow?==?0)
return?0;
const?int?ncol?=?grid[0].size();
vector<vector<int>>?minSum(nrow,?vector<int>(ncol,?0));
minSum[0][0]?=?grid[0][0];
for(int?col?=?1;?col?minSum[0][col]?=?minSum[0][col?-?1]?+?grid[0][col];
for(int?row?=?1;?row?minSum[row][0]?=?minSum[row?-?1][0]?+?grid[row][0];
for(int?col?=?1;?col?for(int?row?=?1;?row?minSum[row][col]?=?min(minSum[row?-?1][col],?minSum[row][col?-?1])?+?grid[row][col];
}
}
return?minSum[nrow?-?1][ncol?-?1];
}
邊界條件定義在矩陣的邊界上。只有一種方法可以獲得邊界上的點(diǎn):從上一個(gè)點(diǎn)向右或向下移動(dòng)一個(gè)格子。大家可以在下方鏈接中試著編寫并測(cè)試一下自己的解決方案。(鏈接地址:https://leetcode.com/problems/minimum-path-sum/?ref=hackernoon.com)給定兩個(gè)整數(shù)數(shù)組val[0..n - 1]和wt [0 . .n-1],分別表示與n個(gè)物品相關(guān)的值和權(quán)重。同時(shí),給定一個(gè)代表背包容量的整數(shù)W,求val [?]的最大值子集,保證這個(gè)子集的權(quán)重之和小于或等于W。背包里的物品都必須保持完整,要么選擇完整的物品,要么不選(0 - 1屬性)。試著想出一個(gè)遞歸解決方案。在此基礎(chǔ)上,添加一個(gè)緩存層,我們就會(huì)得到一個(gè)自上而下的動(dòng)態(tài)規(guī)劃解決方案了!意思是,對(duì)于每一樣物品,我們都有兩個(gè)選擇:- 我們可以把這樣物品放到背包里(如果合適的話),背包的總價(jià)值增加,容量減少。
- 我們可以放棄這樣物品,背包里的價(jià)值和容量不變。
在試過所有組合之后,我們只選擇最大值。這個(gè)過程極其緩慢,但卻是邁向最終解決方案的第一步。我們必須在兩個(gè)選項(xiàng)之間做出決定(向集合中添加一個(gè)元素或跳過它),在許多問題中都面臨這樣的選擇,所以我們一定要了解,并理解其應(yīng)用場(chǎng)合和方式。//?Recursive.?Try?to?turn?this?into?a?piece?of?top-down?DP?code.int?knapSack(int?W,?int?wt[],?int?val[],?int?n)?{
????if?(n?==?0?||?W?==?0)
????????return?0;
????if?(wt[n?-?1]?>?W)
????????return?knapSack(W,?wt,?val,?n?-?1);
????else
????????return?max(val[n?-?1]?+?knapSack(W?-?wt[n?-?1],??wt,?val,?n?-?1),?knapSack(W,?wt,?val,?n?-?1));
}
//?C?style,?in?case?you?are?not?familiar?with?C++?vectorsint?knapSack(int?W,?int?wt[],?int?val[],?int?n)?{
????int?i,?w;
????int?K[n?+?1][W?+?1];
????for?(i?=?0;?i?<=?n;?i++)?{
????????for?(w?=?0;?w?<=?W;?w++)?{
????????????if?(i?==?0?||?w?==?0)
????????????????K[i][w]?=?0;
????????????else?if?(wt[i?-?1]?<=?w)
????????????????K[i][w]?=?max(?val[i?-?1]?+?K[i?-?1][w?-?wt[i?-?1]],?K[i?-?1][w]);
????????????else
????????????????K[i][w]?=?K[i?-?1][w];
????????}
????}
????return?K[n][W];
}
給定兩個(gè)字符串text 1和text 2,返回它們最長(zhǎng)公共子序列的長(zhǎng)度。字符串的子序列是在不改變其余字符相對(duì)順序的情況下,從原字符串中刪除一些字符(也可以不刪除)后生成的新字符串,例如,“ace”是“abcde”的子序列,但“aec”不是。兩個(gè)字符串共同的子序列就被稱為其公共子序列。- 輸入:text 1 = “abcde”, text 2 = “ace”
- 說明:最長(zhǎng)公共子序列是?“ace” ,且其長(zhǎng)度為3
同樣,計(jì)算最長(zhǎng)X的問題,動(dòng)態(tài)規(guī)劃應(yīng)該可以幫得上忙。鑒于大家已經(jīng)有了一些動(dòng)態(tài)規(guī)劃的經(jīng)驗(yàn)了,我就直接從示例中的兩個(gè)屬性說起。我們將字符串稱為A和B,這個(gè)問題的解為f(A, B),解題思路是看最后兩個(gè)字符是否相等:- 如果相等,那么LCS的長(zhǎng)度至少為1。我們需要調(diào)用f(A[0:n-1], B[0:n-1])來查找該索引前的LCS,并加1,因?yàn)锳[n]和B[n]是相同的。
- 如果不相等,我們就刪除兩個(gè)字符串的最后一個(gè)字符——一次刪一個(gè),并查找生成LCS的路徑。換句話說,我們?nèi)(A[0: n-1], B)和f(A, B[0:n-1])的最大值。
- 重疊子問題:我們來看看可能會(huì)出現(xiàn)的調(diào)用:(“abcde”, “ace”)產(chǎn)生x1 = (“abcd”, “ace”)和y1 = (“abcde”, “ac”);x1將產(chǎn)生x12 = (“abc”, “ace”) 和y12= (“abcd”, “ac”);y1將產(chǎn)生(“abcd”, “ac”)和(“abcde”, “a”)。如你所見,同樣的問題需要計(jì)算很多次。
- 最優(yōu)子結(jié)構(gòu):與最長(zhǎng)遞增子序列非常類似。如果我們?cè)谄渲幸粋€(gè)字符串A’中添加一個(gè)額外的字符,就可以從所有的緩存結(jié)果中快速計(jì)算出解決方案,而這些結(jié)果是我們解A和B得到的。
雖然用例子來證明理論并不是開始數(shù)學(xué)證明的好方法,但是對(duì)于應(yīng)付編程面試來說已經(jīng)綽綽有余了。int?longestCommonSubsequence(const?string?&text1,?const?string?&text2)?{
const?int?n?=?text1.length();
const?int?m?=?text2.length();
vector<vector<int>>?dp(n?+?1,?vector<int>(m?+?1,0));
for(int?i?=?1;?i?<=?n;?i++){
??for(int?j?=?1;?j?<=?m;?j++){
????if(text1[i-1]?==?text2[j-1])
??????dp[i][j]?=?dp[i-1][j-1]+1;
????else?
??????dp[i][j]?=?max(dp[i-1][j],?dp[i][j-1]);
????}
}
return?dp[n][m];
}
大家可以在下方鏈接中試著編寫并測(cè)試一下自己的解決方案。(鏈接地址:https://leetcode.com/problems/longest-common-subsequence/?ref=hackernoon.com) 總結(jié)
總結(jié)
我們一定要了解這些問題,因?yàn)楹芏嗥渌麊栴}都只是在此基礎(chǔ)上的變種而已,但是不要死記硬背。主動(dòng)去了解動(dòng)態(tài)規(guī)劃的使用場(chǎng)景和應(yīng)用方式,并堅(jiān)持練習(xí),直到可以輕松地將自己的想法轉(zhuǎn)換成代碼。如你所見,這是需要講究方法的。我們不一定要用到高級(jí)的算法或數(shù)據(jù)結(jié)構(gòu)知識(shí)才能解決問題,數(shù)組就足夠了。我沒有完成時(shí)間/空間復(fù)雜度分析,大家可以把它作為課后練習(xí)。歡迎大家隨時(shí)在評(píng)論中留言,提出問題或分享觀點(diǎn)。原文鏈接:
https://hackernoon.com/all-you-need-to-know-about-dynamic-programming-0tj3e5l
本文由AI科技大本營(yíng)翻譯,轉(zhuǎn)載請(qǐng)注明出處
 動(dòng)態(tài)規(guī)劃
動(dòng)態(tài)規(guī)劃 ? ? ?
? ? ? 遞歸和動(dòng)態(tài)規(guī)劃
遞歸和動(dòng)態(tài)規(guī)劃 如何解決動(dòng)態(tài)規(guī)劃問題
如何解決動(dòng)態(tài)規(guī)劃問題 示例
示例 總結(jié)
總結(jié)