算法與數(shù)據(jù)結(jié)構(gòu)（五）哈希表

在講哈希表之前，我們先來看看往一個數(shù)組插入數(shù)據(jù)的過程。

1.確認(rèn)插入數(shù)據(jù)的下標(biāo)；2.把數(shù)據(jù)放入數(shù)組。

拿日常生活中根據(jù)身高排隊(duì)的例子來說，我們想獲取到從低到高的姓名列表。我們就是在重復(fù)這樣一個過程：

1.找到剩余隊(duì)伍中身高最低人的姓名；2.放入當(dāng)前數(shù)組元素的末尾；3.重復(fù)上過程。

但是這里有很大的限制，就是我們這種情況下能夠知道一個姓名對應(yīng)數(shù)組的下標(biāo)是多少，很多其他情況下是無法知道的。在這種情況下使用數(shù)組處理這個場景是足夠的。

然后看看這樣一個場景，我們需要存儲一個人的姓名及其對應(yīng)的身高。這個時候我們用數(shù)組會怎么做？我們可以把數(shù)組存儲的元素改成是 (姓名, 身高)，然后我們查找一個人的身高時，遍歷數(shù)組找到姓名，然后返回身高。這種做法問題是查找時間復(fù)雜度過高，每次查找有 O(n) 的復(fù)雜度。我們能不能在 O(1) 的時間復(fù)雜度中查找到元素呢？

這時候就需要哈希表 HashTable。

什么是哈希表

哈希表 HashTable，也叫散列表、映射、字典等等，哈希表存儲的是鍵值對 —— key、value。

也就是說，哈希表可以直接存儲 "name": height 來解決上述問題。

哈希表關(guān)鍵點(diǎn)有三個：

?哈希函數(shù)?哈希沖突?裝載因子

哈希函數(shù)

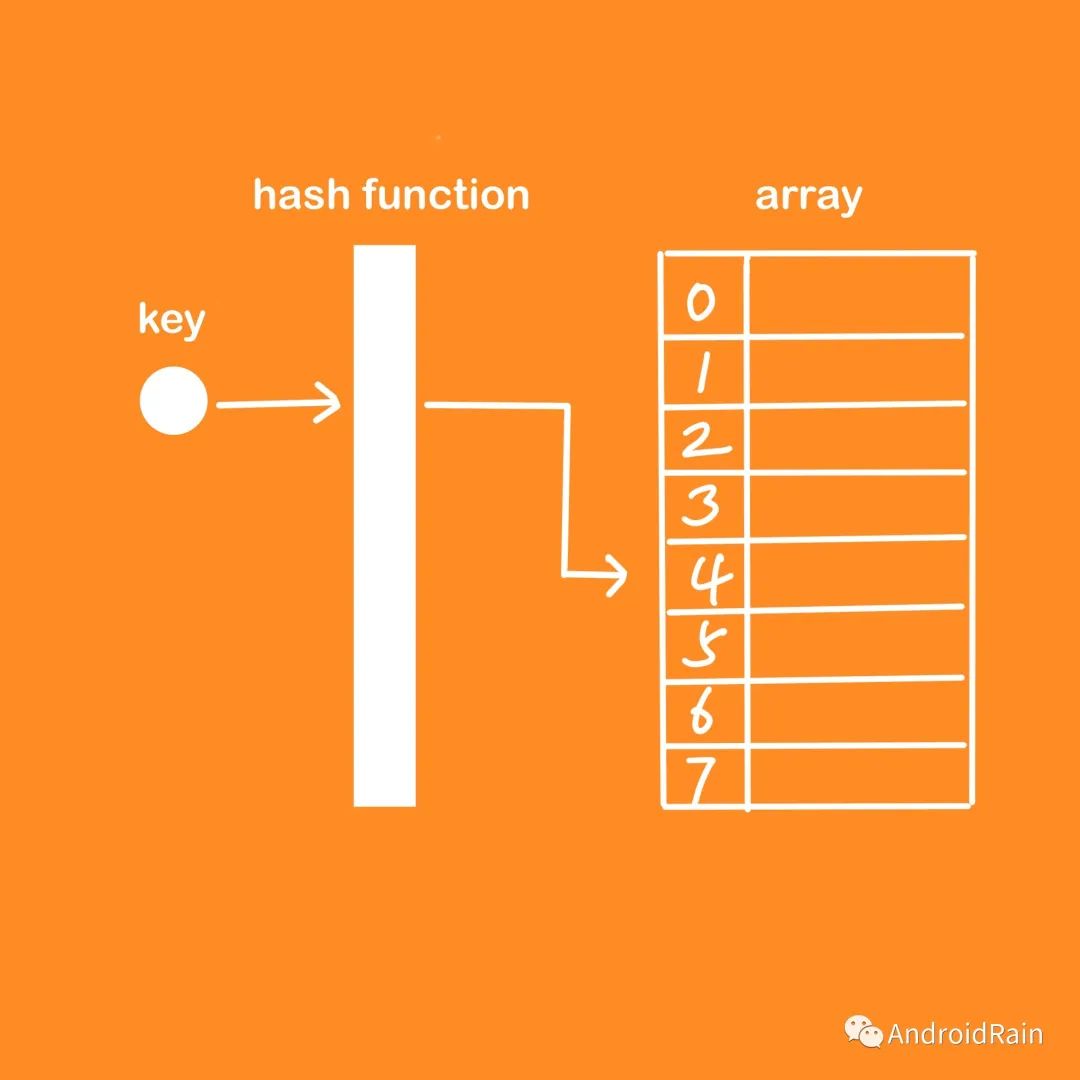
接下來我們結(jié)合上圖解釋一下哈希函數(shù)。

我們現(xiàn)在要往哈希表中放入 ("xiaoming", 175) 這組數(shù)據(jù)。發(fā)生了什么事情呢？

首先，數(shù)據(jù)的 key = "xiaoming" 會經(jīng)過哈希表的哈希函數(shù)，轉(zhuǎn)換成數(shù)組的下標(biāo) i。然后，我們把 value = 175 存儲到 array[i] 的位置。

這里的哈希函數(shù)要滿足幾個特性：

1.相同的 key 經(jīng)過哈希函數(shù)之后的輸出一致；2.不同的 key 經(jīng)過哈希函數(shù)之后的輸出不同；3.哈希函數(shù)產(chǎn)生的輸出在數(shù)組的有效范圍內(nèi)。

當(dāng)我們在哈希表中查詢 "xiaoming" 的身高時，哈希函數(shù)先計算該 key 對應(yīng)的數(shù)組下標(biāo)，然后取出數(shù)組中的數(shù)據(jù)。

這里我們可以看到，哈希表 = 哈希函數(shù) + 數(shù)組，哈希表其實(shí)是數(shù)組的一種擴(kuò)充，是由數(shù)組演化而來的，解決數(shù)組所無法解決的問題。這里我們也再強(qiáng)調(diào)一下，沒有一種最優(yōu)的數(shù)據(jù)結(jié)構(gòu)和算法，只有更加適合某種場景、解決某種問題的數(shù)據(jù)結(jié)構(gòu)和算法。

后續(xù)我們可以看到，哈希表也可能是另外一種形式：哈希表 = 哈希函數(shù) + 數(shù)組 + 鏈表。

哈希沖突

你可能會想到，在我們存儲過程中，雖然我們能夠通過哈希函數(shù)得到一個 key 的整數(shù)值，但是我們的數(shù)組是有限的，假設(shè)這里的整數(shù)值為 k，數(shù)組長度為 n。我們通過 k % n 取余操作拿到 k 實(shí)際的數(shù)組下標(biāo)。我們就會碰到兩個整數(shù)對 n 取余之后的下標(biāo)是相等的情況。比如 3 % 2 == 5 % 2 的情況。這個時候如果數(shù)組這個位置已經(jīng)放置了元素，我們該怎么處理呢？

因?yàn)槭枪：瘮?shù)輸出的值產(chǎn)生了沖突，所以這種情況我們稱之為哈希沖突或者哈希值沖突。

而對應(yīng)的解決辦法有兩種：

1.開放尋址法2.鏈表法

開放尋址法

開放尋址法中有線性探測法，該方法是說在發(fā)生沖突時，我們就依次在數(shù)組中往后查找，直到找到一個空閑位置。但是這種方法，在我們插入數(shù)據(jù)越來越多時，發(fā)生沖突的可能性就越來越大，線性探測時間也就越來越長。這時哈希表的插入、查找時間復(fù)雜度會退化，最差情況是 O(n)。Java 中的 ThreadLocalMap 使用此方法來解決哈希沖突。

當(dāng)我們采用線性探測法時，如何對以上問題做出優(yōu)化呢？

此時我們就要引入裝填因子的概念，裝填因子 = 已有元素個數(shù) / 散列表的總長度。首先我們確定一個裝填因子，然后當(dāng)目前的因子大于我們設(shè)定的裝填因子時，我們就對數(shù)組進(jìn)行擴(kuò)容，以此來保證有一定的剩余空間，進(jìn)而減少線性探測時的時間復(fù)雜度。裝填因子的設(shè)置也需要根據(jù)情況來看，要對線性探測的執(zhí)行效率和擴(kuò)容的成本上進(jìn)行平衡。本質(zhì)上還是時間、空間的平衡，當(dāng)我們要求哈希表執(zhí)行效率更高時，我們就可以設(shè)置更小的裝填因子，增大剩余的數(shù)組空間，有利我們更快的進(jìn)行線性探測；當(dāng)我們內(nèi)存比較緊張時，就需要設(shè)定更大的裝填因子。

還有一種開放尋址法是雙重散列。當(dāng)一個哈希函數(shù)輸出的下標(biāo)值發(fā)生沖突時，采用另外一種哈希函數(shù)來重新計算下標(biāo)值，直到找到空閑的位置。

鏈表法

鏈表法另辟蹊徑，它把數(shù)組存儲的元素改為鏈表，當(dāng)發(fā)生沖突時不再嘗試把數(shù)據(jù)存入到數(shù)組中，而是存儲到同一下標(biāo)的鏈表之中。上圖展示了鏈表法的哈希表結(jié)構(gòu)。這時我們發(fā)現(xiàn) 哈希表 = 哈希函數(shù) + 數(shù)組 + 鏈表。Java 中的 LinkedHashMap 使用了鏈表法解決沖突問題。

當(dāng)我們插入數(shù)據(jù)時，相當(dāng)于在鏈表中插入元素的時間復(fù)雜度 O(1)。當(dāng)我們查詢時，取決于對應(yīng)鏈表的長度 m，時間復(fù)雜度為 O(m)。

但是對于黑客來說，這種方法存在一個致命漏洞。黑客可以不斷的往哈希表中放入 key 對應(yīng)下標(biāo)相同的數(shù)據(jù)，這會導(dǎo)致數(shù)組中只有該位置有長長的鏈表，進(jìn)而導(dǎo)致查詢時間十分漫長，對你的程序產(chǎn)生攻擊的效果。我們稱之為哈希表碰撞攻擊。

所以一個能夠產(chǎn)生均勻下標(biāo)值的哈希函數(shù)十分重要。除了采用更優(yōu)的哈希函數(shù)，我們還可以對鏈表做優(yōu)化，比如說改造成紅黑樹解決查找過慢的問題。其實(shí) Java 8 中就做了這個優(yōu)化。

經(jīng)過以上分析，我們知道開放尋址法更加適合數(shù)據(jù)量比較小、裝填因子較小的場景，這也是 Java 中 ThreadLocalMap 使用開放尋址法的原因；鏈表法比較適合存儲數(shù)據(jù)量比較大、對象比較大的情況。

什么是好的哈希表

結(jié)合上述內(nèi)容，我們知道一個好的哈希表要有以下特性：

?快速的查詢、插入、刪除?性能穩(wěn)定，不能夠退化的太嚴(yán)重?內(nèi)存占用合理

要保證以上特性，需要做到：

?哈希函數(shù)的輸出比較均勻?合適的裝填因子大小，高性能的動態(tài)擴(kuò)容?合適的哈希沖突解決方法

總結(jié)

我們除了要了解哈希表是存儲鍵值對的數(shù)據(jù)結(jié)構(gòu)之外，還要掌握插入、刪除、搜索一個數(shù)據(jù)的發(fā)生過程是怎樣的。另外我們也要掌握哈希表的三個關(guān)鍵要素：哈希函數(shù)、沖突解決方法、裝填因子。最后，我們要根據(jù)自己的實(shí)際場景，通過調(diào)整確定三個關(guān)鍵要素，選擇合適的哈希表或者實(shí)現(xiàn)自己的哈希表。

實(shí)踐

最后，推薦大家做一下 Leetcode 上的題目。可以先用自己的思路寫一下代碼，然后結(jié)合使用哈希表的方式再寫一份代碼。最后比較這兩者的時間空間復(fù)雜度。

?有效的字母異位詞^[1]?兩數(shù)之和^[2]?三數(shù)之和^[3]

References

[1] 有效的字母異位詞: https://leetcode-cn.com/problems/valid-anagram/
[2] 兩數(shù)之和: https://leetcode-cn.com/problems/two-sum/
[3] 三數(shù)之和: https://leetcode-cn.com/problems/3sum/