五十四、最基礎(chǔ)的冒泡排序
「@Author:Runsen」
排序可能是所有的算法中最最基礎(chǔ)和最最常用的了。排序是一個(gè)非常經(jīng)典的問(wèn)題,它以一定的順序?qū)σ粋€(gè)數(shù)組(或一個(gè)列表)中的項(xiàng)進(jìn)行重新排序。
排序算法有很多種,每個(gè)都有其自身的優(yōu)點(diǎn)和局限性。
今天我們來(lái)學(xué)習(xí)最最簡(jiǎn)單的冒泡排序算法。
冒泡排序
要學(xué)習(xí)冒泡排序必須知道它的原理:
所謂冒泡,就是將元素兩兩之間進(jìn)行比較,誰(shuí)大就往后移動(dòng),直到將最大的元素排到最后面,接著再循環(huán)一趟,從頭開(kāi)始進(jìn)行兩兩比較,而上一趟已經(jīng)排好的那個(gè)元素就不用進(jìn)行比較了。
下面,我們就進(jìn)入代碼環(huán)節(jié)。
Python實(shí)現(xiàn)冒泡排序
現(xiàn)在,我給你一個(gè)nums = [3,1,25,6,8,10,15],要求你用Python將nums實(shí)現(xiàn)冒泡排序。
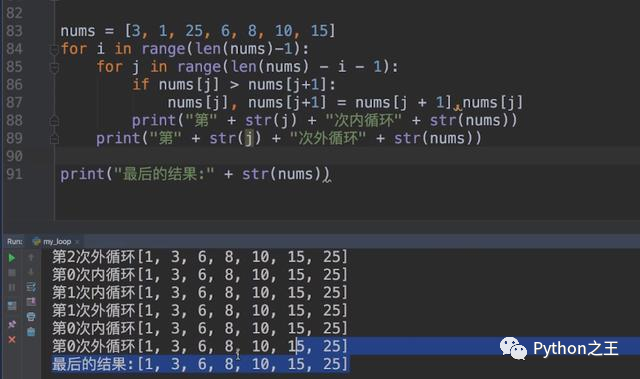
看上去很難入手,其實(shí)很簡(jiǎn)單,我先給出代碼
nums?=?[3,1,25,6,8,10,15]
for?i?in?range(len(nums)-1):
????for?j?in?range(len(nums)?-?i?-1):
????????if?nums[j]?>?nums[j+1]:
????????????nums[j],nums[j+1]?=??nums[j+1],nums[j]
????????print("第"+str(j)+"次內(nèi)循環(huán)"+str(nums))
????print("第"+str(i)+"次外循環(huán)"+str(nums))
print("最后的結(jié)果"+str(nums))
我們先遍歷nums,這不就是我們的range(len(nums)-1),至于為什么是range(len(nums)-1),其實(shí)就是我們的下標(biāo)從0開(kāi)始的,len(nums)返回是7,range是左開(kāi)右閉,但是冒泡排序,我們只需要取到nums[5] = 10 就足夠了,所以這里range(len(nums)-1),取到[3,1,25,6,8,10]。
然后,我們?cè)诒闅v之后的nums,比如i = 0,我們將j取值范圍到len(nums) - i -1,用nums[j] > nums[j+1]判斷兩兩的大小, 每次內(nèi)循環(huán)將最大的移到最右邊。
每一次內(nèi)循環(huán)的目的就是將當(dāng)中最大的移到最右邊,而每一次外循環(huán)的目的就是當(dāng)最大的移到最右邊后,縮小范圍,再尋找最大的數(shù),再把它移到最右邊。
我們執(zhí)行上面的代碼的結(jié)果如下:
第0次內(nèi)循環(huán)[1,?3,?25,?6,?8,?10,?15]
第1次內(nèi)循環(huán)[1,?3,?25,?6,?8,?10,?15]
第2次內(nèi)循環(huán)[1,?3,?6,?25,?8,?10,?15]
第3次內(nèi)循環(huán)[1,?3,?6,?8,?25,?10,?15]
第4次內(nèi)循環(huán)[1,?3,?6,?8,?10,?25,?15]
第5次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第0次外循環(huán)[1,?3,?6,?8,?10,?15,?25]
第0次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第1次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第2次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第3次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第4次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第1次外循環(huán)[1,?3,?6,?8,?10,?15,?25]
第0次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第1次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第2次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第3次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第2次外循環(huán)[1,?3,?6,?8,?10,?15,?25]
第0次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第1次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第2次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第3次外循環(huán)[1,?3,?6,?8,?10,?15,?25]
第0次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第1次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第4次外循環(huán)[1,?3,?6,?8,?10,?15,?25]
第0次內(nèi)循環(huán)[1,?3,?6,?8,?10,?15,?25]
第5次外循環(huán)[1,?3,?6,?8,?10,?15,?25]
最后的結(jié)果[1,?3,?6,?8,?10,?15,?25]
我們可以看到,第0次外循環(huán),已經(jīng)將25放在了最右邊,第1次外循環(huán)確定把15放到最右邊,這樣從右往左,從大到小,這就是完整的冒泡排序。
冒泡排序的時(shí)間復(fù)雜度是:假設(shè)被排序的數(shù)列中有N個(gè)數(shù)。遍歷一趟的時(shí)間復(fù)雜度是,需要遍歷多少次呢?N-1次!因此,冒泡排序的時(shí)間復(fù)雜度。
冒泡排序是穩(wěn)定的算法:它滿(mǎn)足穩(wěn)定算法的定義;所謂算法穩(wěn)定性指的是對(duì)于一個(gè)數(shù)列中的兩個(gè)相等的數(shù)a[i]=a[j],在排序前,a[i]在a[j]前面,經(jīng)過(guò)排序后a[i]仍然在a[j]前,那么這個(gè)排序算法是穩(wěn)定的。
下面是Java冒泡排序代碼。
public?class?Sort?{
??public?static?void?sort()?{
????Scanner?input?=?new?Scanner(System.in);
????int?sort[]?=?new?int[10];
????int?temp;
????System.out.println("請(qǐng)輸入10個(gè)排序的數(shù)據(jù):");
????for?(int?i?=?0;?i???????sort[i]?=?input.nextInt();
????}
????for?(int?i?=?0;?i?1;?i++)?{
??????for?(int?j?=?0;?j?1;?j++)???????{
????????if?(sort[j]?1])?{
??????????temp?=?sort[j];
??????????sort[j]?=?sort[j?+?1];
??????????sort[j?+?1]?=?temp;
????????}
??????}
????}
????System.out.println("排列后的順序?yàn)椋?);
????for(int?i=0;i??????System.out.print(sort[i]+"???");
????}
??}
??public?static?void?main(String[]?args)?{
????sort();
??}
}
JavaScript冒泡排序代碼。
function?sort(arr)?{
????for?(var?i?=?0;?i?1;?i++)?{??//外部for循環(huán)
????????for?(var?j?=?0;?j?1;?j++)?{
????????????if?(arr[j]?>?arr[j?+?1])?{
????????????????var?temp?=?arr[j];
????????????????arr[j]?=?arr[j?+?1];
????????????????arr[j?+?1]?=?temp;
????????????}
????????}
????}
????return?arr;
}
//舉例如下
var?arr?=?sort([1,?7,?4,?97,?23,?45]);
console.log(arr);
?本文已收錄 GitHub,傳送門(mén)~[1] ,里面更有大廠面試完整考點(diǎn),歡迎 Star。
?
Reference
傳送門(mén)~: https://github.com/MaoliRUNsen/runsenlearnpy100
更多的文章
點(diǎn)擊下面小程序
- END -

