職業(yè)規(guī)劃高級(jí)前端可視化低代碼

點(diǎn)擊上方 趣談前端，關(guān)注公眾號(hào)

回復(fù)進(jìn)群，加入前端交流群

1. 介紹

1.1 什么是數(shù)據(jù)可視化？

可視化是利用計(jì)算機(jī)圖形學(xué)和圖像處理技術(shù)，將數(shù)據(jù)轉(zhuǎn)換成圖形或者圖像在屏幕上顯示出來，再進(jìn)行交互處理的理論、方法和技術(shù)。

數(shù)據(jù)可視化并不是簡單的將數(shù)據(jù)變成圖表，而是以數(shù)據(jù)為視角，看待世界。數(shù)據(jù)可視化就是將抽象概念形象化表達(dá)，將抽象語言具體化的過程。

1.2 為什么要用數(shù)據(jù)可視化

首先我們利用視覺獲取的信息量絕對(duì)遠(yuǎn)遠(yuǎn)的比別的感官要多得多。
它能幫助分析的人對(duì)數(shù)據(jù)有更全面的認(rèn)識(shí)，下面舉個(gè)??

我們看下面幾組數(shù)據(jù)：

對(duì)數(shù)據(jù)進(jìn)行簡單的數(shù)據(jù)分析，每組數(shù)據(jù)都有兩個(gè)變量 X 和 Y，然后用常用的統(tǒng)計(jì)算法評(píng)估其特點(diǎn)。

Means（平均值）：X = 9Y = 7.5
Variance（總體方差）：X = 11Y = 4.122
Line regression（線性回歸方程）：Y = 3.0 + 0.5X

猛一看，你會(huì)覺得數(shù)據(jù)都是同一個(gè)特點(diǎn)。但如果通過可視化方式展示出來，就會(huì)有不同效果

人類大腦在記憶能力的限制。實(shí)際上我們觀察物體的時(shí)候，我們大腦和計(jì)算機(jī)一樣有長期的記憶（memory 硬盤）和短期記憶（cache 內(nèi)存），只要我們讓短期記憶中的文字、物體等一遍遍的鞏固，它們才可能進(jìn)入長期記憶。很多研究表明，在進(jìn)行理解和學(xué)習(xí)的時(shí)候，圖文更有效的幫助我們記憶，也更有趣，容易理解。

1.3 常見的前端開發(fā)中有什么可視化工具

對(duì)于在 Data 部門或者做跟數(shù)據(jù)相關(guān)工作的同學(xué)，一定對(duì)可視化不陌生，常見的場(chǎng)景有大屏、3D 展示等等。同樣，現(xiàn)階段前端層面涌現(xiàn)出多種可視化方案，這里簡單羅列幾種：

Echarts，可以流暢的運(yùn)行在 PC 和移動(dòng)設(shè)備，且兼容絕大部分瀏覽器（IE 8/9/10），底層使用 ZRender 作為渲染引擎，提供直觀、交互豐富、可高度個(gè)性化定制的數(shù)據(jù)圖表。
Antv，是螞蟻金服新一代數(shù)據(jù)可視化解決方案，致力于提供一套簡單方便、專業(yè)可靠、無限可能的數(shù)據(jù)可視化最佳實(shí)踐。其包括 G（可視化引擎）、G2（可視化圖表）、G6（圖可視化引擎）、F2（移動(dòng)可視化方案）、L7（地理空間數(shù)據(jù)可視化）。
D3，其實(shí)一個(gè)可以基于數(shù)據(jù)來操作文檔的 JavaScript 庫，其遵循現(xiàn)有 Web 標(biāo)準(zhǔn)，可以不需要其他任何框架運(yùn)行在現(xiàn)代瀏覽器中。

1.4 前端可視化圖表是怎么繪制出來的

這里我們只簡單介紹 2D 的繪制方案。

Canvas。其基于位圖的圖像。其使用 JavaScript 程序繪圖（動(dòng)態(tài)生成），提供的功能更原始，適合圖像處理、動(dòng)態(tài)渲染以及大數(shù)據(jù)量繪制。優(yōu)點(diǎn)如下：

性能高，可以自己控制繪制過程。
可控性高（像素級(jí)別）。
內(nèi)存占用恒定（與像素點(diǎn)個(gè)數(shù)有關(guān)）。

Svg。其基于矢量的圖像。適合用來做動(dòng)態(tài)生成，且容易編輯。

不失真，放大縮小都清晰。
學(xué)習(xí)成本低，其也是一種 DOM 結(jié)構(gòu)。
使用方便，設(shè)計(jì)軟件即可導(dǎo)出（icon 就是這樣實(shí)現(xiàn)的）。

聽了上面的介紹，似乎感覺對(duì)可視化有了一定的了解，但它到底是怎么繪制出來的以及交互是怎么做的呢？

2. 如何實(shí)現(xiàn)繪圖（Canvas 版本）

先不要著急，在介紹如何繪圖之前，我們先來了解幾個(gè)專業(yè)名詞：

包圍盒。包圍盒是一種求解離散點(diǎn)集最優(yōu)包圍空間的算法，基本思想是用體積稍大且特性簡單的幾何體（稱為包圍盒）來近似地代替復(fù)雜的幾何對(duì)象，常見的包圍盒算法有 AABB 包圍盒、包圍球以及固定方向凸包 FDH。包圍盒算法是進(jìn)行碰撞干涉初步檢測(cè)的重要方法。
貝塞爾曲線，是應(yīng)用于二維圖形應(yīng)用程序的數(shù)學(xué)曲線。其由線段和節(jié)點(diǎn)組成，節(jié)點(diǎn)是可拖動(dòng)的支點(diǎn)，線段像可伸縮的皮筋，它的計(jì)算參數(shù)公式為

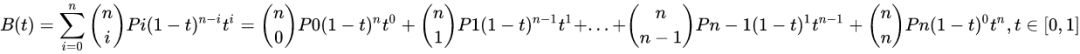
插值函數(shù)，簡單理解就是在離散數(shù)據(jù)的基礎(chǔ)上補(bǔ)差連續(xù)函數(shù)，使得這條連續(xù)曲線通過全部給定的離散數(shù)據(jù)點(diǎn)。
B 樣條基函數(shù)。令 U={u0,u1,…,um} 是一個(gè)單調(diào)不減的實(shí)數(shù)序列，即 ui<=ui+1，i=0,1,…,m-1。其中，ui 稱為節(jié)點(diǎn)，U 稱為節(jié)點(diǎn)矢量，用 Ni,p (u) 表示第 i 個(gè) p 次 B 樣條基函數(shù)，其定義為：

B 樣條基有如下性質(zhì)：

遞推性
局部支承性
規(guī)范性
可微性

看完上面的一連串專業(yè)名稱，先別著急腦袋暈，下面我們看看怎么用 Canvas 繪制一條線

2.1 繪制一條線

線是可視化中最常見的圖形元素了，最常見的就是折線圖

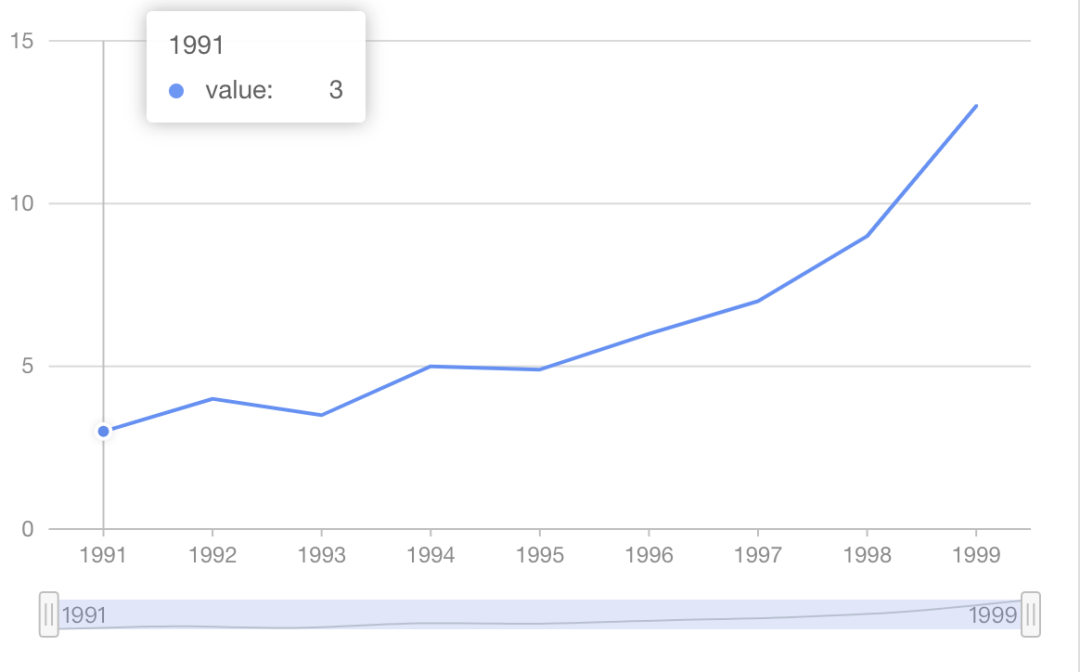
一條線是由多個(gè)點(diǎn)來定義，按照點(diǎn)和點(diǎn)之間的連接方式不同，我們可分為 “折線” 和 “曲線”，在可視化渲染時(shí)又能分為 “虛線” 和 “實(shí)線”。

換個(gè)思路，我們用線來繪制閉合的路徑，從而形成封閉區(qū)域，就能實(shí)線面積圖和雷達(dá)圖，就像這樣。

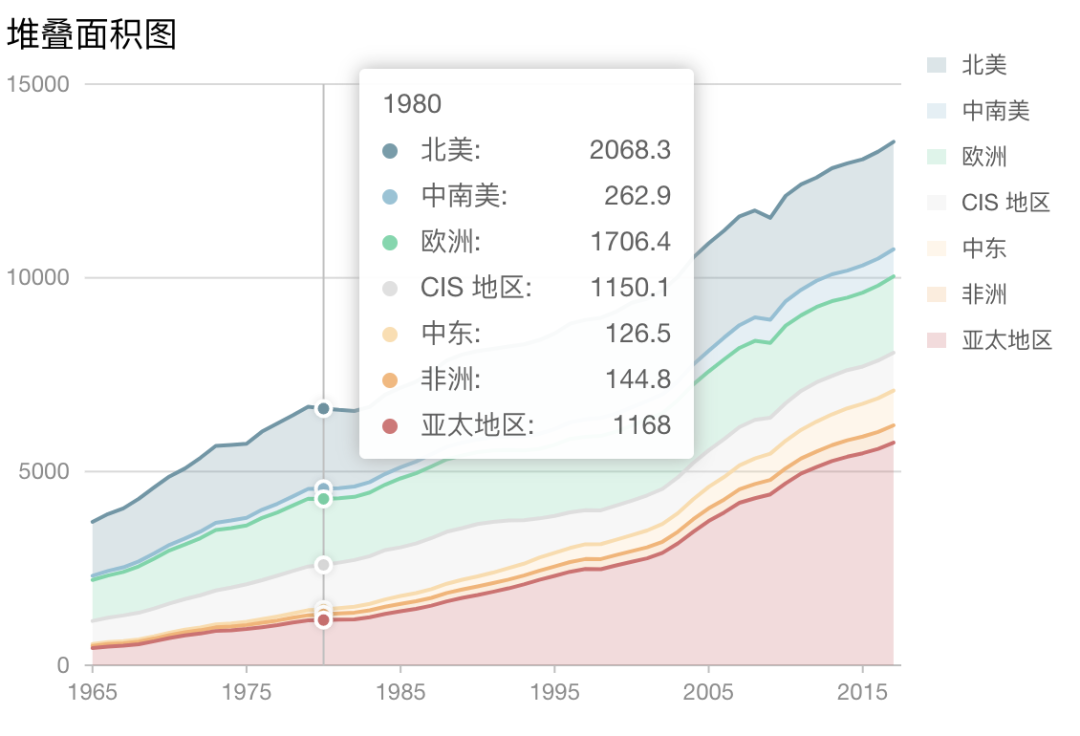
下面我們來看看到底如何繪制一個(gè)線圖呢？

2.1.1 什么是線？

我們都知道，線是由點(diǎn)組成的，兩個(gè)相鄰的點(diǎn)連接起來就成為一個(gè) “段”，多個(gè)段拼裝組成一條線，就像這樣。

轉(zhuǎn)化成程序思維我們可以得知：

點(diǎn)有坐標(biāo)（x, y）
段有起點(diǎn)、終點(diǎn)且它們都是點(diǎn)，還有長度以及順序
線有若干個(gè)段也有若干個(gè)點(diǎn)

2.2 實(shí)現(xiàn)折線

2.2.1 獲取段

折線拆分為段的實(shí)現(xiàn)很簡單，根據(jù)傳入的點(diǎn)數(shù)據(jù)，相鄰兩點(diǎn)劃為一段。下面簡單演示一下（大概寫個(gè)邏輯）：

getSegment(points, defined) {  segCache ← [];
  totalLength ← 0;
  for p, i
    pnext ← points[i + 1]
    if pnext
      // 兩個(gè)點(diǎn)確定一條段 調(diào)用對(duì)應(yīng)函數(shù)
      segment = CreateSegment
      // 緩存數(shù)據(jù)
      segCache ← segment
      // 計(jì)算段的長度
      segment.length ← distance
      // 計(jì)算總長度
      totalLen ·····
      // 判斷是否空段
      if ···
        // 一些邏輯
  // 返回段和總長度      
}

實(shí)現(xiàn)很簡單，依次遍歷點(diǎn)數(shù)據(jù)，初始化段對(duì)象，這里有個(gè)計(jì)算段長度的邏輯，段的長度要用后面會(huì)說到，至于長度怎么算，很簡單就不說了。上面有個(gè)判斷是否為空段的邏輯，之所以做這個(gè)操作是因?yàn)樵趯?shí)際應(yīng)用中，有些業(yè)務(wù)場(chǎng)景需要隱藏某些段，可以看看下面的圖：

2.2.2 使用 Canvas 繪制線段

Canvas 提供了兩個(gè) API —— moveTo 和 lineTo，具體操作中我們需要調(diào)用 moveTo 將畫筆定位到線段的起點(diǎn)，然后通過 lineTo 繪制到線段的終點(diǎn)即可，如果多個(gè)首尾相接的線段可以忽略 moveTo（Canvas 內(nèi)部存儲(chǔ)當(dāng)前上下文），直接 lineTo。

基于上述方法，我們只需要遍歷一條線中所有段，依次連接就可以了，為了處理空段，我們需要設(shè)置一個(gè) start 的標(biāo)記變量，如果處于 start 狀態(tài)，會(huì)先 moveTo 到新的點(diǎn)，而不是 lineTo，大概代碼如下：

drawLine(ctx) {
  defined ← false
  // 設(shè)置開始標(biāo)志（先moveTo）
  lineStart
  for i ← 0 to len
    seg ← segCache[i]
    ...
    if i = len
      lineEnd
      strokeLine
    else
        // 判斷是否為空段
        if ...
          drawSeg //否
        else
          lineStart // 是
}
drawSeg(seg, ctx) {
  if lineStart
    moveTo
  ····
  drawLine
}
drawLine(x, y, ctx) {
  lineTo
}

這塊可能會(huì)有個(gè)疑惑，感覺把線拆成段繪制好像更麻煩了，多了一個(gè)拆段的步驟，為什么不直接連接點(diǎn)呢？這樣劃分相當(dāng)于拆分了不同結(jié)構(gòu)，那么每個(gè)結(jié)構(gòu)下的元素都有自己的定制化，可視化層面可能展示的樣式等等不同。比如說下面的，通過這樣的靈活拼裝，提升了擴(kuò)展性，同時(shí)在其他方面也有優(yōu)勢(shì)，下面會(huì)具體介紹。

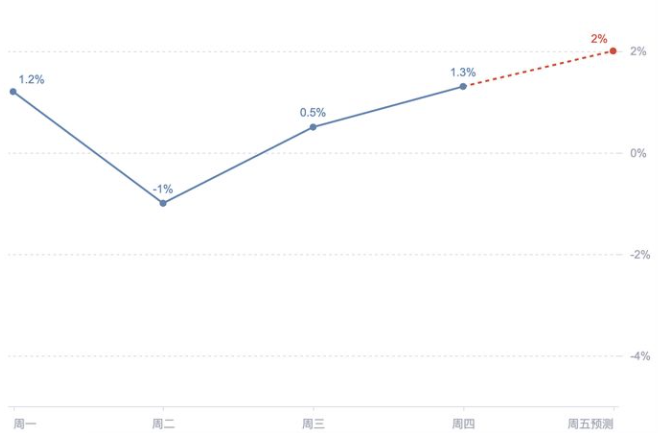
2.3 實(shí)現(xiàn)曲線

2.3.1 貝塞爾曲線

前面我們簡單介紹了貝塞爾曲線，Canvas 也支持貝塞爾二次和三次曲線，通常使用三次貝塞爾曲線畫法。下面我們?cè)敿?xì)講解一下。

Bézier curve（貝塞爾曲線）是應(yīng)用于二維圖形應(yīng)用程序的數(shù)學(xué)曲線。貝塞爾曲線點(diǎn)的數(shù)量決定了曲線的階數(shù)，一般 N 個(gè)點(diǎn)構(gòu)成的 N-1 階貝塞爾曲線，即 3 個(gè)點(diǎn)為二階。一般我們都會(huì)要求曲線至少包含 3 個(gè)點(diǎn)，因?yàn)閮蓚€(gè)點(diǎn)的貝塞爾曲線是一條直線。按順序，第一個(gè)點(diǎn)為 起點(diǎn) ，最后一個(gè)點(diǎn)為 終點(diǎn) ，其余點(diǎn)都為 控制點(diǎn) 。

下面以二次貝塞爾曲線為例。

2.3.1.1 二次貝塞爾曲線

給定點(diǎn) P0,P1,P2，P0 和 P2 為起點(diǎn)和終點(diǎn)，P1 為控制點(diǎn)。從 P0 到 P2 的弧線即為一條二次貝塞爾曲線。

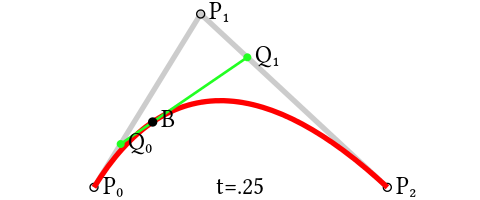
在這里我們要將整個(gè)曲線的繪制量化為從 0~1 的過程，用 t 為當(dāng)前過程的進(jìn)度，t 的區(qū)間即 0~1。每一條線都需要根據(jù) t 生成一個(gè)點(diǎn)，如下圖，一個(gè)點(diǎn)從 P0 移動(dòng)到 P1，這是這條線從 0~1 的過程。

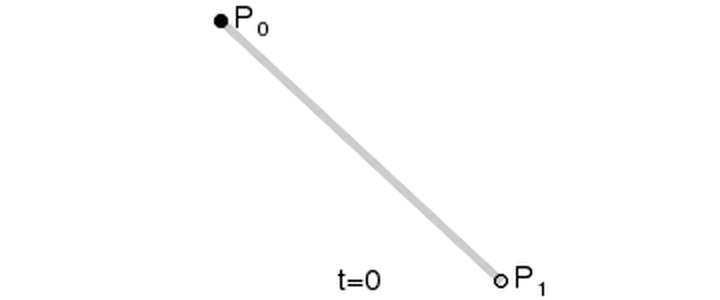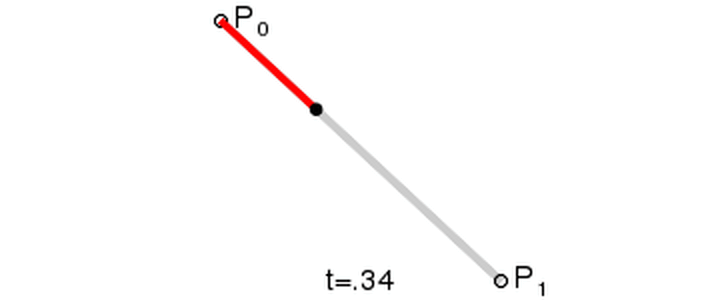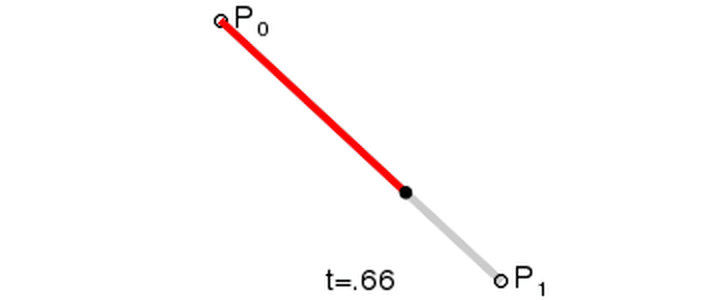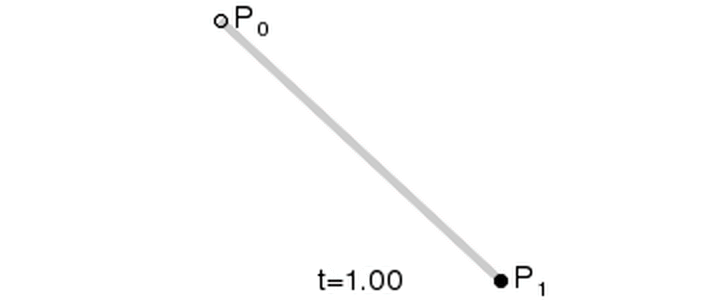
下面我們還原一下一個(gè)二次貝塞爾曲線的生成過程。

首先我們鏈接 P0P1,P1P2，得到兩條線段。然后我們對(duì)進(jìn)度 t 進(jìn)行取值，比如 0.3，取一個(gè) Q0 點(diǎn)，使得 P0Q0 的長度為 P0P1 總長度的 0.3 倍。

同時(shí)我們?cè)?P1P2 上取一點(diǎn) Q1，使得 P0Q0: P0P1 = P1Q1: P1P2。接下來我們?cè)僭?Q0Q1 上取一點(diǎn) B，使得 P0Q0: P0P1 = P1Q1: P1P2 = Q0B:Q0Q1。

現(xiàn)在我們得到的點(diǎn) B 就是二次貝塞爾曲線的上的一個(gè)點(diǎn)，如果我們使 t=0 開始取值，逐步遞增進(jìn)行插值，就會(huì)得到一系列的點(diǎn) B，進(jìn)行連接就會(huì)形成一條完整的曲線。

最終經(jīng)過數(shù)據(jù)推導(dǎo)，我們得到了二次貝塞爾曲線公式（具體推導(dǎo)我們不搞了，感興趣可以去百度看看）。

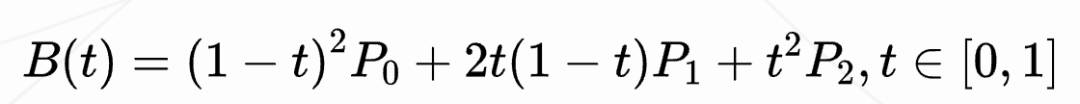
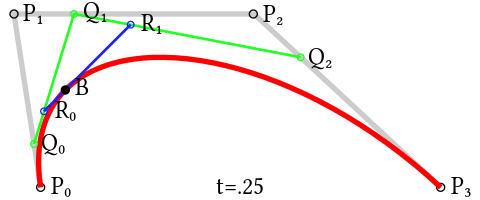
2.3.1.2 三次貝塞爾曲線

三次貝塞爾曲線由四個(gè)點(diǎn)組成，通過更多的迭代步驟來確定曲線上的點(diǎn)。

2.3.2 使用 Canvas 繪制貝塞爾曲線

在 Canvas 中繪制三次貝塞爾曲線使用 bezierCurveTo() 方法，具體參數(shù)定義可以在 MDN 上查閱，這里不羅列了。

2.3.3 樣條曲線與獲取段

了解了如何繪制三次貝塞爾曲線，我們回到實(shí)際場(chǎng)景，一個(gè)線圖會(huì)有若干個(gè)數(shù)量的點(diǎn)連接生成。但只使用 Canvas 提供的功能，并不能滿足這個(gè)需求。前面我們繪制折線是提出了段的概念，如果我們將一條完整的曲線拆分成多個(gè)段，每個(gè)段都是個(gè)三次貝塞爾曲線，問題好像就可以解決。那么問題就轉(zhuǎn)化為如何生成多個(gè)貝塞爾曲線且它們能平滑連接。

上面我們介紹概念時(shí)提出了樣條曲線，可能大家也沒看懂，是有些抽象。簡單將就是有一個(gè)點(diǎn)的集合，分成多段曲線，各曲線處的連接點(diǎn)處可以平滑連接，轉(zhuǎn)化成數(shù)學(xué)術(shù)語就是說連接點(diǎn)有連續(xù)的一次和二次導(dǎo)數(shù)且一次和二次導(dǎo)數(shù)相同。下面我們看個(gè)??

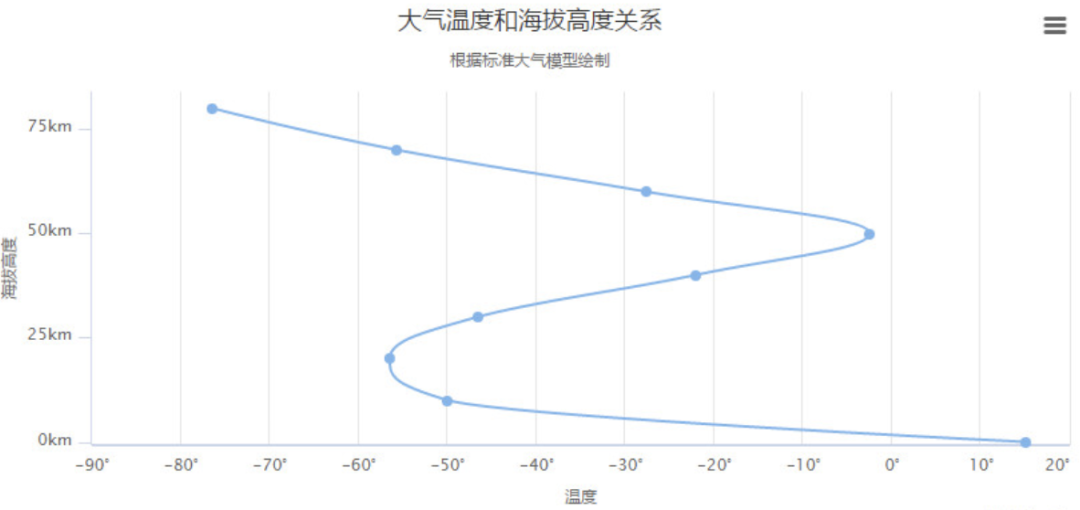
上面這個(gè)圖是由多個(gè)三次貝塞爾曲線拼接而成，我們要將其劃分前，需要確定幾個(gè)參數(shù)：

每條三次貝塞爾曲線的起點(diǎn)和終點(diǎn)
每條三次貝塞爾曲線的兩個(gè)控制點(diǎn)

只有當(dāng)我們選擇合適的起點(diǎn)、終點(diǎn)和控制點(diǎn)，相鄰的兩條曲線才能平滑連接。拆分算法很多，這里不詳細(xì)介紹了（其實(shí)我也看不懂），我們實(shí)現(xiàn)可以直接用 d3-shape 的 Curves 接口。下面用 Basis 算法的實(shí)現(xiàn)用例，我們簡單了解一下。

getSegment(points, defined){
  segCache ← []
  totalLen ← 0
  if points.len < 3
    getSegment  start, end, controll1, controll2
  for i ← 0 to points.len - 2
    first ← points[i]
    second ← points[i + 1]
    third ← points[i + 2]
    if i = 0
      start ← first
    else
      start ← end
    
    // 計(jì)算起點(diǎn)、終點(diǎn)、控制點(diǎn)
    // 計(jì)算長度
    // 補(bǔ)算最后點(diǎn)
}

這段邏輯也比較簡單，循環(huán)給到的點(diǎn)，從當(dāng)前索引位置開始向后取三個(gè)點(diǎn)，根據(jù)這個(gè)三個(gè)點(diǎn)以及當(dāng)前段的起始點(diǎn)計(jì)算結(jié)束點(diǎn)和控制點(diǎn)。每個(gè)新段的起點(diǎn)是上個(gè)段的終點(diǎn)。但是當(dāng)前循環(huán)邏輯不會(huì)計(jì)算最后一個(gè)點(diǎn)，所以會(huì)少一段，最后加個(gè)單獨(dú)邏輯處理。

2.3.4 點(diǎn)的計(jì)算

我們用一個(gè)簡單的公式來計(jì)算各個(gè)點(diǎn)的值（公式結(jié)合 B 樣條曲線和三次貝塞爾曲線在端點(diǎn)處的一階和二階導(dǎo)出得到），這里不介紹具體公式推導(dǎo)。

if (i === 0) {
  start = first
} else {
  start = end
}
end = Point((first.x + 4 * second.x + third.x) / 6, (first.y + 4 * second.y + third.y) / 6)
controll1 = Point((2 * first.x + second.x) / 3, (2 * first.y + second.y) / 3)
controll2 = Point((first.x + 2 * second.x) / 3), (first.y + 2 * second.y) / 3 )

2.3.5 曲線分割與長度計(jì)算

聽起來這不是一個(gè)容易的事情。由于貝塞爾曲線是插值函數(shù)，所以計(jì)算只能先對(duì)曲線進(jìn)行切割，然后計(jì)算足夠小的這一小段的曲線近似長度，再累加。這個(gè)計(jì)算量有點(diǎn)大，不過有大神給了個(gè)思路傳送門。

找到連接的點(diǎn)。假設(shè)我要在 t=0.25 的位置將當(dāng)前曲線切分成兩條曲線，首先我們要知道點(diǎn) B 的位置。根據(jù)公式代入即可。
獲取控制點(diǎn)。拿到點(diǎn) B 之后，其為第一段的終點(diǎn)，第二段的起點(diǎn)，我們需要計(jì)算控制點(diǎn)。根據(jù)數(shù)學(xué)邏輯，我們可以得出：

第一段曲線的第一個(gè)控制點(diǎn)的運(yùn)動(dòng)軌跡是線段 P0P1，和 t 線性相關(guān)
第一段曲線的第二個(gè)控制點(diǎn)的運(yùn)動(dòng)軌跡是線段 Q0Q1，和 t 線性相關(guān)
第二段曲線的第一個(gè)控制點(diǎn)的運(yùn)動(dòng)軌跡是線段 Q1Q2，和 t 線性相關(guān)
第二段曲線的第二個(gè)控制點(diǎn)的運(yùn)動(dòng)軌跡是線段 P2P3，和 t 線性相關(guān)

根據(jù)上面結(jié)論，拆分就很簡單了。(這塊代碼有點(diǎn)長，就不寫了)

長度計(jì)算。我們可以在任意位置對(duì)三次貝塞爾曲線進(jìn)行拆分了，結(jié)合二分法，控制迭代次數(shù)，結(jié)合近似長度計(jì)算函數(shù)，我們可以得到想要精度的長度值了。（代碼也不寫了）
獲取段。現(xiàn)在我們需要處理最后一個(gè)點(diǎn)的特殊邏輯，這里將第二個(gè)點(diǎn)和第三個(gè)點(diǎn)都用最后一個(gè)點(diǎn)表示。

first ← points[i - 2]
second ← points[i - 1]
third ← points[i -1]
start ← end
end ← third

···
···

曲線畫法。前面都準(zhǔn)備好了，現(xiàn)在只需要調(diào)用 Canvas 的 API 就能畫線了。

2.4 怎么處理動(dòng)畫

前面我們遺留了一個(gè)問題，為什么需要計(jì)算長度？

我們已經(jīng)完成了線的繪制，如何做少量的改動(dòng)實(shí)現(xiàn)動(dòng)畫呢？我們可以了解到不管直線和曲線，我們都分了很多段，而這些段都是和 t 相關(guān)的。

2.4.1 方案

動(dòng)畫的本質(zhì)就是在一定的時(shí)間內(nèi)繪制某一部分區(qū)域，我們將整個(gè)線條區(qū)域劃分到 [0, 10] 區(qū)間，啟動(dòng)一個(gè)循環(huán)，每次繪圖時(shí)更新 t 的值，在上面循環(huán)繪制 segment 的代碼中，將整條線圖的 t 轉(zhuǎn)化為每一個(gè)段內(nèi)部的 t 值，段內(nèi)部根據(jù) t 值對(duì)自身切割，只畫應(yīng)該繪制的那部分即可。

由于我們已經(jīng)計(jì)算了每個(gè)段的長度和總長度，所以每個(gè)段的占比可以計(jì)算，此占比再和整個(gè)線圖的 t 值進(jìn)行換算即可。這個(gè)思路其實(shí)就是 局部繪制。

但對(duì)于面積圖，其實(shí)會(huì)分為兩組 segment 繪制，繪制時(shí)我們會(huì)發(fā)現(xiàn)在同一個(gè) t 時(shí)，在 x 方向的位移是不同步的。繪制動(dòng)畫從左向右推進(jìn)，比如繪制第一段時(shí)，計(jì)算第一段應(yīng)該被繪制的區(qū)間，最后填充上下兩段的閉合區(qū)間，但有個(gè)問題，如果相同的 t，代入不同組 segment 的函數(shù)中，產(chǎn)生的 x 值不一樣，那么繪制的效果就不對(duì)了，切面會(huì)是斜的。

解決這個(gè)問題做法是根據(jù) x 或者 y 值反求 t 值，再代入目標(biāo)函數(shù)中。對(duì)于三次貝塞爾曲線來說，這又是一個(gè)大難題，由于篇幅所限及代碼實(shí)現(xiàn)的比較復(fù)雜，這里不講了（其實(shí)我不會(huì)，但這有地方會(huì)）。

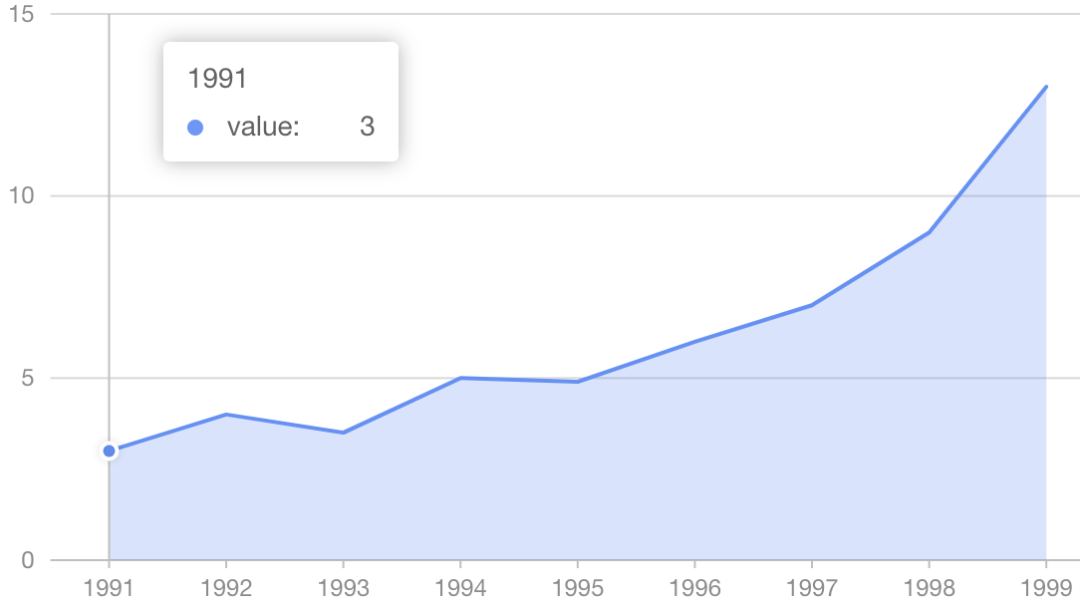
2.5 交互

交互無非是點(diǎn)一點(diǎn)，摸一摸。但從上面我們得知，一條線有那么多點(diǎn)，怎么知道鼠標(biāo)觸發(fā)的是那個(gè)點(diǎn)呢？

2.5.1 Canvas 的拾取方案

繪制時(shí) Canvas 不會(huì)保存繪制圖形的信息，一旦繪制完成用戶在瀏覽器中其實(shí)是一個(gè)由無數(shù)像素點(diǎn)組成的圖片，用戶點(diǎn)擊時(shí)無法從瀏覽器自帶的 API 獲取點(diǎn)擊到的圖形。常見的拾取方案有以下幾種：

使用緩存 Canvas 通過顏色拾取圖形
使用 Canvas 內(nèi)置的 API 拾取圖形
使用幾何圖形包圍盒
混雜上面的幾種方式

上面的各種拾取方案各有利弊，下面來詳細(xì)的介紹各種方案的實(shí)現(xiàn)方式和一些問題，最后對(duì)比一下性能。

2.5.1.1 使用緩存 Canvas 方案

使用緩存的 Canvas 來進(jìn)行圖形的拾取步驟如下：

在顯示的 Canvas 上繪制圖形
在緩存（隱藏）的 Canvas 上重新繪制一下所有的圖形，使用圖形的索引值作為圖形的顏色來繪制圖形
在顯示的 Canvas 進(jìn)行點(diǎn)擊，獲取緩存 Canvas 上對(duì)應(yīng)位置的像素點(diǎn)，將像素的顏色轉(zhuǎn)換成數(shù)字，這個(gè)數(shù)字就是圖形的索引值

優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

實(shí)現(xiàn)簡單，只需要將圖形繪制兩遍即可
拾取性能好，核心的拾取算法復(fù)雜度 O(1)

缺點(diǎn)

渲染開銷加倍
畫布過大時(shí)獲取緩存數(shù)據(jù) getImageData() 方法開銷很大，會(huì)降低快速拾取的收益

適合的場(chǎng)景和不適宜的場(chǎng)景

適合的場(chǎng)景

圖形的數(shù)量比較大、重繪不頻繁的場(chǎng)景
支持局部刷新的場(chǎng)景效果更好

不適合的場(chǎng)景

頻繁動(dòng)畫的場(chǎng)景，兩倍的渲染開銷和獲取緩存數(shù)據(jù)方法的開銷過大，性能反而降低
圖形的數(shù)據(jù)量很小的情況下優(yōu)勢(shì)不明顯

性能檢測(cè)

繪制顯示的 10000 個(gè)圖形 6ms
在緩存的圖形 14ms ，增加了將數(shù)字轉(zhuǎn)換成顏色的開銷
獲取緩存的圖片數(shù)據(jù) getImageData() 的開銷 14ms
圖形拾取的開銷 0.1ms

2.5.1.2 使用內(nèi)置 API

Canvas 標(biāo)簽提供了一個(gè)接口 isPointInPath() 來獲取對(duì)應(yīng)的點(diǎn)是否在繪制的圖形內(nèi)部，操作步驟如下：

繪制所有圖形
進(jìn)行拾取時(shí)，調(diào)用 isPointInPath() 方法判斷點(diǎn)是否在圖形中。

優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

實(shí)現(xiàn)簡單，僅使用 Canvas 原生的接口
不會(huì)拖慢首次渲染的時(shí)間

缺點(diǎn)

性能差，每次檢測(cè)都得走一遍圖形的繪制
僅能檢測(cè)是否被包圍，不能檢測(cè)是否在線上

適合的場(chǎng)景

圖形的量非常小，小于 100 個(gè)時(shí)
可以配合包圍盒檢測(cè)、四分樹檢測(cè)一起使用

性能檢測(cè)

拾取 10000 個(gè)圖形的時(shí)間 2000ms

2.5.1.3 幾何包圍盒檢測(cè)方案

最開始我們提到了包圍盒，現(xiàn)在有了使用的地方。

Canvas 上繪制的圖形都是標(biāo)準(zhǔn)的幾何圖形，點(diǎn)、線、面的檢測(cè)在幾何算法中比較成熟，每個(gè)圖形在繪制時(shí)都會(huì)給其生成一個(gè)包圍盒并保存，當(dāng)拾取圖形時(shí)可以直接使用數(shù)據(jù)運(yùn)算檢測(cè)。

檢測(cè)過程如下：

反序檢測(cè)所有的圖形
判斷點(diǎn)是否在圖形的包圍盒內(nèi)，如果不在，則返回 false
如果圖形繪制線，則判斷是否在線上
如果圖形被填充，則判斷是否被包圍

優(yōu)缺點(diǎn)

優(yōu)點(diǎn)

圖形檢測(cè)算法比較成熟
思路比較清晰，優(yōu)化潛力大，可以通過各種緩存機(jī)制優(yōu)化檢測(cè)性能
不會(huì)影響圖形的渲染性能

缺點(diǎn)

實(shí)現(xiàn)復(fù)雜，特別是一些貝塞爾曲線和非閉合曲線的檢測(cè)性能比較差
在存在大量分層的場(chǎng)景下，每個(gè)分層上有 transform 的存在，矩陣運(yùn)算大大降低運(yùn)算的性能

適合的場(chǎng)景

使用范圍廣

性能檢測(cè)：

10000 個(gè)點(diǎn)的檢測(cè)性能 5 - 20ms

2.5.1.4 混雜拾取

在實(shí)例的應(yīng)用過程中并非使用某一種拾取方案，通常將多種拾取方案混合使用，大致分為以下方案：

包圍盒 + 緩存 Canvas：使用緩存 Canvas 時(shí)需要緩存的 Canvas 的大小跟原始 Canvas 的大小保持一致，但是可以僅僅創(chuàng)建 1*1 的緩存 Canvas，先通過計(jì)算是否在圖形的包圍盒內(nèi)，將所有包含拾取點(diǎn)的圖形在這個(gè)一像素的畫布上進(jìn)行繪制（需要進(jìn)行 translate 將畫布中心定位到拾取的點(diǎn)上）, 然后對(duì)這一像素進(jìn)行顏色的檢測(cè)。
注意：這種混雜模式對(duì)于簡單圖形” 圓 “、” 矩形 “ 的拾取并不比單純的幾何算法更快。
包圍盒 + isPointInPath: 簡單的圖形使用幾何算法，復(fù)雜的很多填充的圖形可以使用包圍盒檢測(cè)和 Canvas 內(nèi)置的 isPointInPath 來檢測(cè)。

2.5.1.5 總結(jié)

在 Canvas 上拾取圖形時(shí)的方案選擇與用戶的場(chǎng)景密切相關(guān)，不同的場(chǎng)景適用的方案也不同：

在圖形數(shù)量少，不需要精確拾取的場(chǎng)景下（移動(dòng)端）可以直接使用 isPointInPath 方法
在畫布不頻繁刷新、圖形量大的場(chǎng)景下適合使用緩存的 Canvas 的方法
使用幾何算法的拾取方案幾乎適合于所有的場(chǎng)景，但是需要配合各種緩存機(jī)制，并注意矩陣乘法帶來的開銷
上面的幾種方法可以混合使用，拾取的優(yōu)化無止境，但是滿足需求即可。

3. 總結(jié)

上述全文介紹了什么是可視化，緊接著我們分析了線圖的實(shí)現(xiàn)方案以及圖形的交互實(shí)現(xiàn)。總結(jié)來說，可視化無時(shí)無刻不存在在我們身邊，看起來好像充滿神秘色彩，但我們仔細(xì)研究會(huì)發(fā)現(xiàn)，實(shí)現(xiàn)可視化并不是一件難事，上述流程如果有出錯(cuò)的地方，還請(qǐng)批評(píng)指正。