說(shuō)起笛卡爾坐標(biāo)系，可能會(huì)讓你回想起中學(xué)里學(xué)習(xí)解析幾何的美（tong）好（ku）時(shí)光。但不管怎樣，應(yīng)該都還記的平面直角坐標(biāo)系以及空間直角坐標(biāo)系。

如果你進(jìn)一步了解過(guò)，會(huì)發(fā)現(xiàn)笛卡爾坐標(biāo)系可以包括笛卡爾直角（rectangular）坐標(biāo)系以及笛卡爾斜角（oblique）坐標(biāo)系。

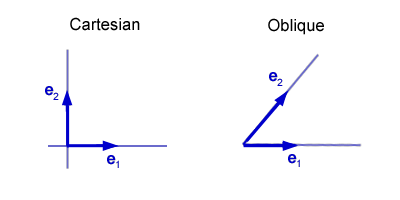
上圖左邊的直角坐標(biāo)系貌似性質(zhì)更好，它應(yīng)該是首先被引入的，而右邊的斜角坐標(biāo)系可以看作直角坐標(biāo)系的推廣。但事實(shí)是否如此呢？

另外，坐標(biāo)系并不復(fù)雜，聰明睿智的古希臘人沒(méi)有想到嗎？為什么到了十七世紀(jì)才提出來(lái)呢？我們來(lái)簡(jiǎn)單地回顧一下歷史。

笛卡爾坐標(biāo)系的由來(lái)

笛卡爾（Cartesian）一詞源自于建立解析幾何的哲學(xué)家兼數(shù)學(xué)家笛卡爾（Descartes）。但是，翻開笛卡爾的《幾何》，你會(huì)發(fā)現(xiàn)，貌似找不到直角坐標(biāo)系、坐標(biāo)系這些概念，甚至連坐標(biāo)這個(gè)術(shù)語(yǔ)都沒(méi)有啊。

1637 年笛卡爾發(fā)表了他的名著《方法論》，而《幾何》只是該書的三個(gè)附錄之一。（插播一下，這個(gè)年份有點(diǎn)面熟啊。同年，明朝牛人宋應(yīng)星的著作《天工開物》初刊。）

荷蘭數(shù)學(xué)家 Frans van Schooten 是推動(dòng)笛卡爾幾何傳播的主要人物之一。1649 年，他和學(xué)生將笛卡爾的《幾何》翻譯成拉丁文，在平面上明確引入了一對(duì)軸的概念，而笛卡爾在著作中并沒(méi)有明確指定和兩個(gè)所謂的軸。大概在 1657 年，Van Schooten 也是建議將笛卡爾坐標(biāo)系擴(kuò)展到三維空間的人之一。后來(lái)在 1659 年和 1661 年翻新的譯本增加了更多人的評(píng)論。最早的坐標(biāo)系也是沒(méi)有負(fù)坐標(biāo)的，最早引入負(fù)坐標(biāo)值的是英國(guó)數(shù)學(xué)家沃利斯（Wallis）。

《幾何》的拉丁譯本對(duì)傳播笛卡爾著作中的思想發(fā)揮了重要作用。大神如牛頓也正是從讀過(guò)的笛卡爾的《幾何》中選了兩個(gè)中心問(wèn)題，即求曲線的切線和求曲線下的面積，也就是所謂的微分和積分問(wèn)題。對(duì)于這兩個(gè)問(wèn)題，萊布尼茨在前面一批數(shù)學(xué)家的基礎(chǔ)上也獨(dú)立提出了他的方法。這個(gè)方法的核心是所謂的特征三角形（characteristic triangle），特征三角形的三條邊就是函數(shù)某點(diǎn)處的，然后他得到了比值。如下圖所示，注意當(dāng)初的軸和軸跟現(xiàn)在是不一樣的。

而坐標(biāo)（coordinate）這個(gè)詞是萊布尼茲在 1693 年左右引入的。1715 年約翰在與萊布尼茲的通信中引入了現(xiàn)在通用的由三個(gè)坐標(biāo)平面建立空間坐標(biāo)系的方法。至于阿基米德早在古希臘就有了微積分的思想，已經(jīng)會(huì)用這種思想計(jì)算一些圖形的面積了，但畢竟沒(méi)有坐標(biāo)系嘛，沒(méi)有得出一般化的理論。

笛卡爾坐標(biāo)（Cartesian coordinates）這個(gè)概念就更晚了，大概是在 1844 年才開始使用的。

在笛卡爾的基礎(chǔ)上，后人還發(fā)展了許多其他坐標(biāo)系，例如牛頓使用了平面極坐標(biāo)，歐拉將其推廣到三維空間等。

笛卡爾提出坐標(biāo)系的思想也有一個(gè)類似牛頓與蘋果的故事，那就是大家聽過(guò)的蜘蛛網(wǎng)的故事。這個(gè)典故與牛頓的蘋果類似，只是八卦，為枯燥的數(shù)學(xué)理論增加了一些談資。

另外，還有關(guān)于那條心形曲線的美麗愛情故事，但講這個(gè)故事時(shí)給出的曲線往往是用極坐標(biāo)來(lái)表示的，而笛卡爾應(yīng)該是不知道這個(gè)曲線的。

笛卡爾幾何

我們都聽說(shuō)過(guò)笛卡爾在《幾何》這個(gè)著作中提出了解析幾何。但是，有個(gè)插曲，在笛卡兒的《方法論》發(fā)表前，另一位法國(guó)數(shù)學(xué)家費(fèi)馬也已經(jīng)完成了用代數(shù)方程研究幾何曲線的大作《平面和立體軌跡引論》，據(jù)說(shuō)早在 1629 年就完稿了，但到了 1679 年才發(fā)表。因此，早于牛頓和萊布尼茲的微積分創(chuàng)建之爭(zhēng)，解析幾何的開創(chuàng)優(yōu)先權(quán)之爭(zhēng)落到了這兩個(gè)大師身上，但后人樂(lè)于稱笛卡兒和費(fèi)馬同為解析幾何之父。

但當(dāng)我們翻開書，發(fā)現(xiàn)找不到笛卡爾坐標(biāo)。事實(shí)上，我們沒(méi)有看到從它的方程中繪制出任何新的曲線。笛卡爾允許什么樣的曲線呢？不是我們可能認(rèn)為的任何具有方程的曲線。他只允許通過(guò)某種機(jī)械設(shè)備根據(jù)特定規(guī)則繪制曲線這種方式來(lái)構(gòu)建的曲線。總之，我們沒(méi)有找到解析幾何這個(gè)術(shù)語(yǔ)，只是一種處理舊問(wèn)題的革命性的新方法。

雖然笛卡爾并沒(méi)有明確提出坐標(biāo)系這一概念，但是后人還是給他冠名了。我們不禁要問(wèn)，為什么呢？

古希臘的成就及問(wèn)題

笛卡爾的思想是橫空出世的嗎？當(dāng)然不是的，跟他的后輩牛頓等人一樣，也是站住巨人的肩膀上的。

近代數(shù)學(xué)的發(fā)展自然離不開古希臘人的貢獻(xiàn)，他們雖然超級(jí)厲害，但也是有缺憾的。我們簡(jiǎn)單回顧下古希臘在數(shù)量運(yùn)算上的遺留問(wèn)題。在這之前先來(lái)看一下他們?nèi)〉玫呐c笛卡爾的研究有關(guān)的成就。

我們知道古希臘畢達(dá)哥拉斯學(xué)派由于不可公度性而拒絕無(wú)理數(shù)，歐多克斯引入了量，建立了比例理論，部分化解了這次危機(jī)。數(shù)也許還存在問(wèn)題，但研究幾何量是沒(méi)有問(wèn)題的。比如勾股定理，古希臘稱為畢達(dá)哥拉斯定理，用現(xiàn)在的符號(hào)表示為，

a^2 + b^2 = c^2

我們說(shuō)這是勾股數(shù)啊，他們看來(lái)，這可以不關(guān)數(shù)，而是看成幾何問(wèn)題。這里一個(gè)量對(duì)應(yīng)某個(gè)線段的長(zhǎng)度，而它的平方自然是指面積了。歐幾里得的證明也是從面積著手，可以看下圖，證明三個(gè)正方形中相同顏色的面積等同即可。

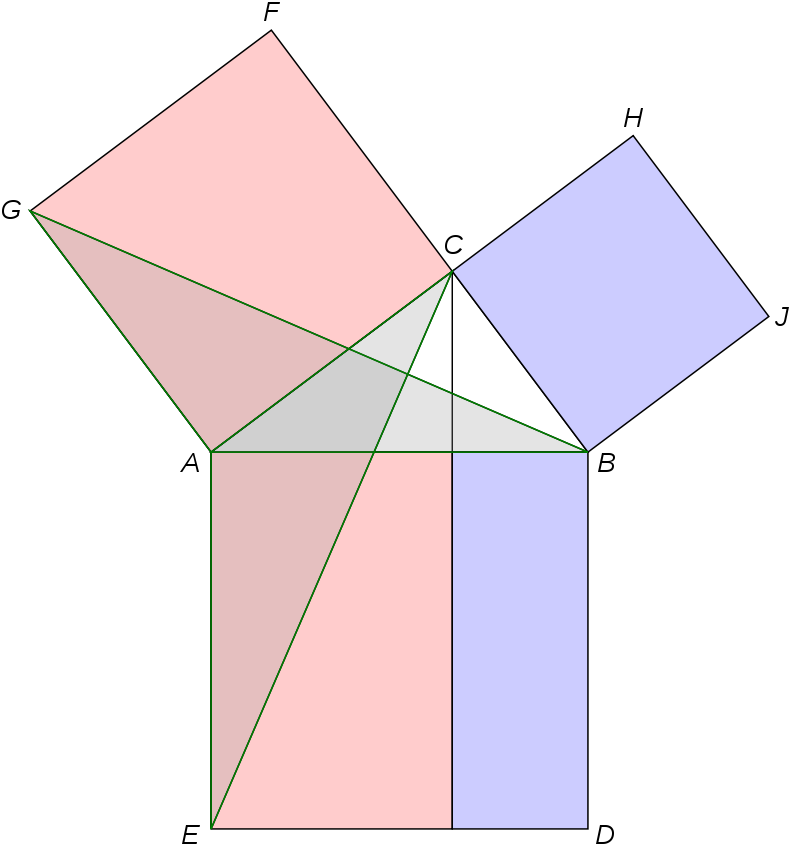
古希臘除了歐幾里得，還有很多數(shù)學(xué)家值得提起，比如歐多克斯、梅內(nèi)赫莫斯、阿基米德、阿波羅尼奧斯以及后期的代數(shù)學(xué)家丟番圖等。

我們來(lái)看一下古希臘三大幾何問(wèn)題之一的倍立方體問(wèn)題，用現(xiàn)在的符號(hào)來(lái)表達(dá)就是，給定，找到使得。

數(shù)學(xué)家希波克拉底（不是那個(gè)醫(yī)生）表示，這個(gè)問(wèn)題可以規(guī)約為在和之間找到兩個(gè)平均比例的問(wèn)題。再次用現(xiàn)在的符號(hào)來(lái)表達(dá)，如果我們可以找到和使得，

\dfrac{a}{x} = \dfrac{x}{y} = \dfrac{y}{2a}

然后，消掉，可以得到。

梅內(nèi)赫莫斯在此基礎(chǔ)上發(fā)現(xiàn)了另一個(gè)有趣的結(jié)論。如果我們只考慮公式的前兩項(xiàng)，

\dfrac{a}{x} = \dfrac{x}{y}

可得，它代表一條拋物線。如果考慮第一項(xiàng)和第三項(xiàng)，得

\dfrac{a}{x} = \dfrac{y}{2a}

即，它表示一條雙曲線。

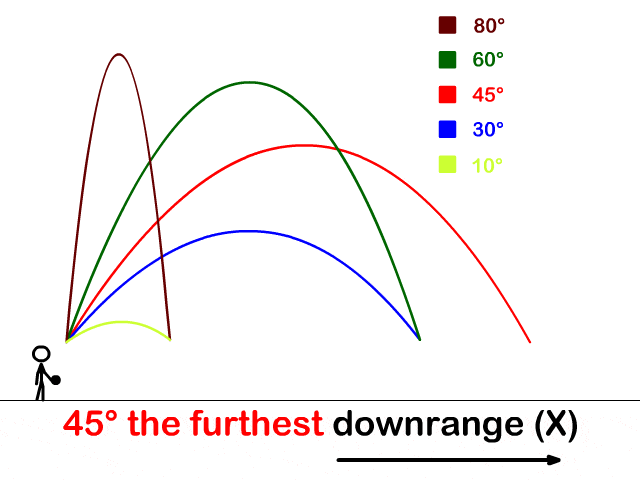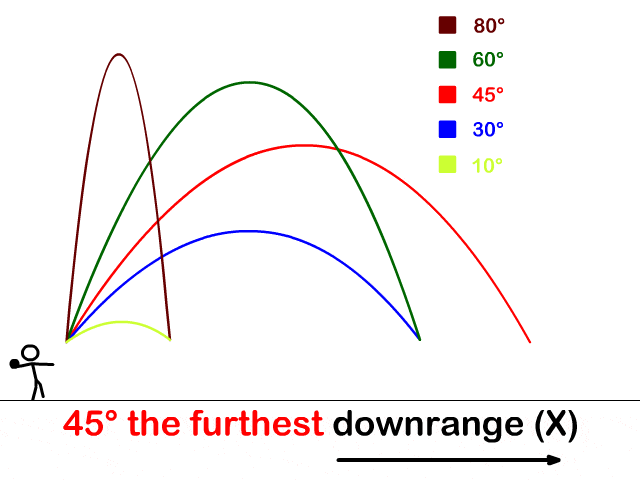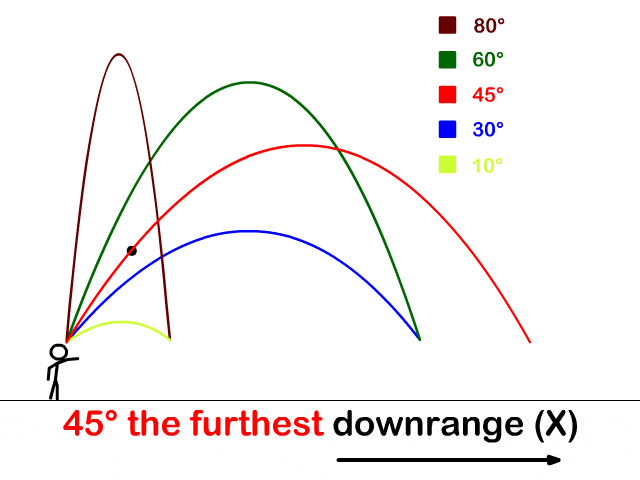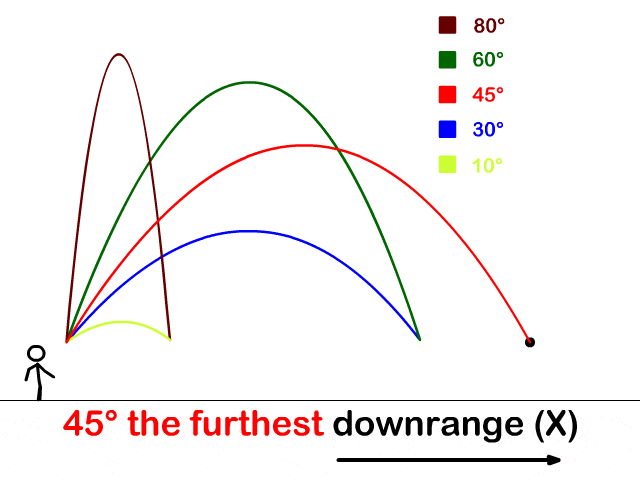
因此，倍立方體問(wèn)題可以轉(zhuǎn)化為找到拋物線和雙曲線的交點(diǎn)的問(wèn)題。其實(shí)還可以找出另一條曲線，用現(xiàn)在的坐標(biāo)系來(lái)繪制這些曲線的話如下圖所示。

正是這種歸約促進(jìn)了希臘人對(duì)圓錐曲線的研究興趣。不過(guò)細(xì)細(xì)一想，這里貌似有個(gè)疑問(wèn)。當(dāng)初并沒(méi)有坐標(biāo)系啊，他怎么發(fā)現(xiàn)這些曲線的軌跡，還知道交于一點(diǎn)的呢？或者不妨假設(shè)他知道兩個(gè)未知量的方程決定了一條曲線，并且已經(jīng)引入坐標(biāo)系來(lái)求解了，那豈不是已經(jīng)建立解析幾何了？

梅內(nèi)赫莫斯也許使用了機(jī)械裝置來(lái)繪制他的曲線。一般認(rèn)為梅內(nèi)赫莫斯使用平面切割圓錐的方法來(lái)研究圓錐曲線。阿波羅尼奧斯總結(jié)前人的成果，著有《圓錐曲線論》。

上過(guò)高中應(yīng)該知道為什么叫圓錐曲線吧，我們來(lái)看一個(gè)動(dòng)圖回顧一下，

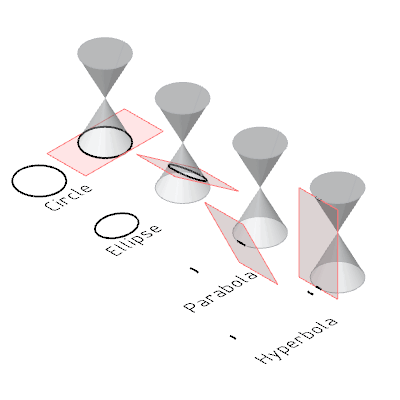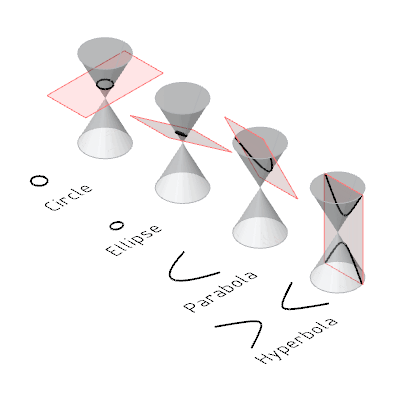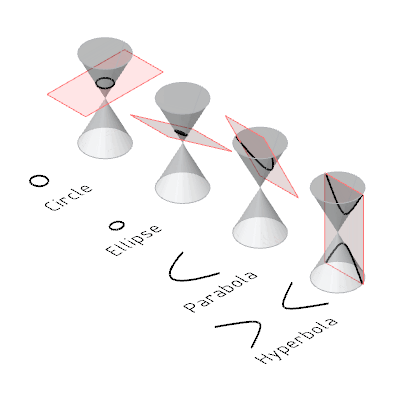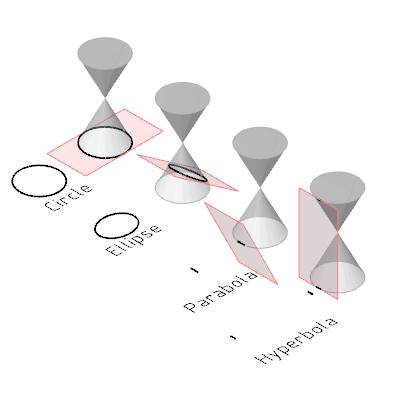
我們不禁要問(wèn)，這曲線在現(xiàn)實(shí)中貌似屬于很特殊的那一類啊，有什么用途呢？另外，既然想到切圓錐了，那隨便切個(gè)西瓜、黃瓜或者別的他們那有的瓜不是可以得到更復(fù)雜的曲線嗎？為什么只研究這么特殊的曲線呢？

有人說(shuō)搞研究好比啃骨頭，先啃軟骨頭，留下硬骨頭給后人。這些曲線形式相對(duì)簡(jiǎn)單，可以用工具繪制。

不過(guò)你還別說(shuō)，雖然簡(jiǎn)單，可能還挺有用。比如后來(lái) 16 世紀(jì)發(fā)生的兩件事，將不接地氣的曲線研究變成了揭示這個(gè)實(shí)現(xiàn)世界的工具。

是德國(guó)天文學(xué)家開普勒（Kepler）繼承哥白尼的日心說(shuō)，并進(jìn)一步揭示出行星環(huán)繞太陽(yáng)運(yùn)行的軌道是一個(gè)橢圓。
意大利物理學(xué)家伽利略 (Galileo）得出物體斜拋運(yùn)動(dòng)的軌道是一條拋物線。

你說(shuō)神不神奇，這自然界的物體運(yùn)動(dòng)軌跡竟然就是圓錐曲線。倍立方體問(wèn)題跟這個(gè)現(xiàn)象貌似風(fēng)馬牛不相及啊，最后卻驚人地聯(lián)系在一起了。

古希臘數(shù)學(xué)家要是接地氣一點(diǎn)，從事一下勞動(dòng)之類的，比如拋個(gè)磚頭什么的，或許老早就能發(fā)現(xiàn)拋物線之類的了啊。奇怪的是，他們卻是從研究倍立方體這么相對(duì)抽象的問(wèn)題中發(fā)現(xiàn)了圓錐曲線。

+問(wèn)題

接著上面，既然通過(guò)數(shù)和量的式子發(fā)現(xiàn)了圓錐曲線，古希臘幾何學(xué)家是不是已經(jīng)認(rèn)識(shí)到曲線與數(shù)量的代數(shù)運(yùn)算之間的聯(lián)系了呢？或者說(shuō)，他們與笛卡爾的解析幾何到底有什么區(qū)別呢？

問(wèn)題可能還是出在他們的研究太不接地氣了，過(guò)于講究邏輯、嚴(yán)謹(jǐn)，一定程度上可以說(shuō)是把自己的思維給禁錮了。比如據(jù)說(shuō)柏拉圖不贊成梅內(nèi)赫莫斯使用機(jī)械設(shè)備來(lái)求解問(wèn)題，他認(rèn)為這會(huì)貶低幾何學(xué)，因?yàn)樵谒磥?lái)幾何學(xué)是人類思維的最高成就。

為了理清問(wèn)題所在，我們來(lái)看一下阿基米德公理：除非一個(gè)量的若干倍可以超過(guò)另一個(gè)量，否則無(wú)法比較兩個(gè)量。因此不允許一條線加上一個(gè)點(diǎn)，或者一個(gè)體積加上一個(gè)面積。比如，寫出這樣的式子是沒(méi)有意義的。

在他們看來(lái)，兩個(gè)數(shù)相加沒(méi)什么問(wèn)題，這是基本的算術(shù)運(yùn)算，但一個(gè)量并不總是能加上另一個(gè)量。比如，我們用和分別表示兩條線段的長(zhǎng)度，那么表示的是一個(gè)面積，此時(shí)式子是什么意思呢? 兩條線段怎么能和一個(gè)面積相加呢? 再比如，三個(gè)量的乘積可以被稱為體積，但是五個(gè)量的乘積對(duì)應(yīng)什么幾何量呢？

也就是說(shuō)，在他們看來(lái)只有相同類型的量才是可能相加的，而且還得對(duì)應(yīng)幾何量。這種對(duì)量的運(yùn)算加以限制的思想，即便到了韋達(dá)那里仍然殘留著。

笛卡爾的前輩，法國(guó)數(shù)學(xué)家韋達(dá)利用歐幾里得的《幾何原本》第一個(gè)提出了無(wú)窮等比級(jí)數(shù)的求和公式，發(fā)現(xiàn)了正切定律、正弦差公式、純角球面三角形的余弦定理等，同時(shí)還發(fā)現(xiàn)了更加著名的韋達(dá)定理。韋達(dá)利用代數(shù)法分析幾何問(wèn)題的思想，正是后繼者笛卡爾解析幾何思想的出發(fā)點(diǎn)。

而笛卡爾通過(guò)引入單位 1，輕巧地打破了對(duì)量運(yùn)算在思維上的限制。進(jìn)而他引入了現(xiàn)在稱為坐標(biāo)系的思想來(lái)展示如何使用代數(shù)來(lái)解決幾何問(wèn)題。

關(guān)鍵一步

笛卡爾和很多前輩一樣，將代數(shù)方程不是當(dāng)作純數(shù)的運(yùn)算，而是指幾何量的運(yùn)算，用幾何術(shù)語(yǔ)來(lái)解釋所有代數(shù)運(yùn)算。為了充分利用代數(shù)的力量，笛卡爾必須想出辦法克服古希臘的思維限制，即在一定意義上必須與過(guò)去進(jìn)行重大決裂。他為代數(shù)方程發(fā)明了一種新的幾何解釋，使代數(shù)學(xué)家擺脫了無(wú)法寫出或等嚴(yán)重限制。

他解放了自己，因此也解放了他的繼任者，包括現(xiàn)在的我們。他選擇了一條他稱之為單位長(zhǎng)度的線段，長(zhǎng)度為，可以任意選擇。這讓他將符號(hào) 解釋為一個(gè)矩形的面積，其中一條邊的長(zhǎng)度為，另一條邊的長(zhǎng)度為。這樣，他就可以放心地寫出，因?yàn)樗梢员徽J(rèn)為是兩個(gè)面積的總和。更重要的是，他將乘積解釋為線的長(zhǎng)度，因此他可以將任意冪解釋為線的長(zhǎng)度。也就是說(shuō)，笛卡爾的線段和的乘積不一定是面積，但可以是另一個(gè)長(zhǎng)度，例如

\dfrac{xy}{x}=\dfrac{y}{1}

并且，還可以把長(zhǎng)度構(gòu)造出來(lái)，如下圖所示。

在這個(gè)例子中，給定一個(gè)單位線段，構(gòu)造和的乘積。讓線段和在起始于的同一條線上下線，讓線段延伸并構(gòu)造平行于的，從而產(chǎn)生比例（因?yàn)?）。因此就是要的乘積。當(dāng)然這是一個(gè)簡(jiǎn)單的構(gòu)造，但他必須明確給出。笛卡爾的幾何哲學(xué)并沒(méi)有讓他僅僅斷言一條線段長(zhǎng)度等于兩條線段長(zhǎng)度的乘積，他還需要構(gòu)建它。

笛卡爾在他的著作《幾何》中分析了當(dāng)時(shí)的幾何學(xué)與代數(shù)學(xué)各自的優(yōu)缺點(diǎn)。他認(rèn)為希臘人的幾何過(guò)多地依賴于圖形，而代數(shù)學(xué)卻完全受法則和公式的限制，以至于阻礙了自由的思想和創(chuàng)造力。

他同時(shí)看到了幾何的直觀與推理的優(yōu)勢(shì)和代數(shù)機(jī)械化運(yùn)算的力量。于是他為了體現(xiàn)存在感（吾思故吾在嘛），稍加思索創(chuàng)立了解析幾何，并拉開了近代數(shù)學(xué)大發(fā)展的序幕。

笛卡爾的坐標(biāo)系

下面我們來(lái)簡(jiǎn)單回顧下笛卡爾在他的《幾何》中引入所謂坐標(biāo)系的內(nèi)容。其中之一個(gè)是對(duì)平面曲線的分類問(wèn)題。

我們先想象有一系列曲線，其中每一類曲線都比它前面的復(fù)雜，首先認(rèn)清如下事實(shí)是將所有這些曲線歸并在一起并依次分類的最好辦法：這些曲線上的所有的點(diǎn)，必定跟某個(gè)直線上的點(diǎn)具有一種確定的關(guān)系，而且這種關(guān)系必須用單個(gè)的方程來(lái)表示，

當(dāng)方程不包含次數(shù)高于兩個(gè)未知量所成的矩形或一個(gè)未知量的平方的項(xiàng)，則曲線屬于第一類，它只包括圓、拋物線、雙曲線和橢圓；
當(dāng)方程包含未知量中的一個(gè)或兩個(gè)的三次或四次的項(xiàng)，則曲線屬于第二類；
當(dāng)方程包含未知量中的一個(gè)或兩個(gè)的五次或六次的項(xiàng)，則曲線屬于第三類；
依此類推。

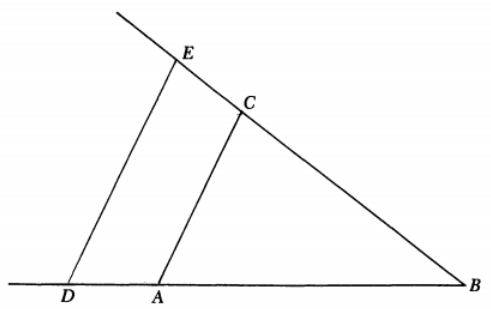
下面請(qǐng)看一個(gè)圖，

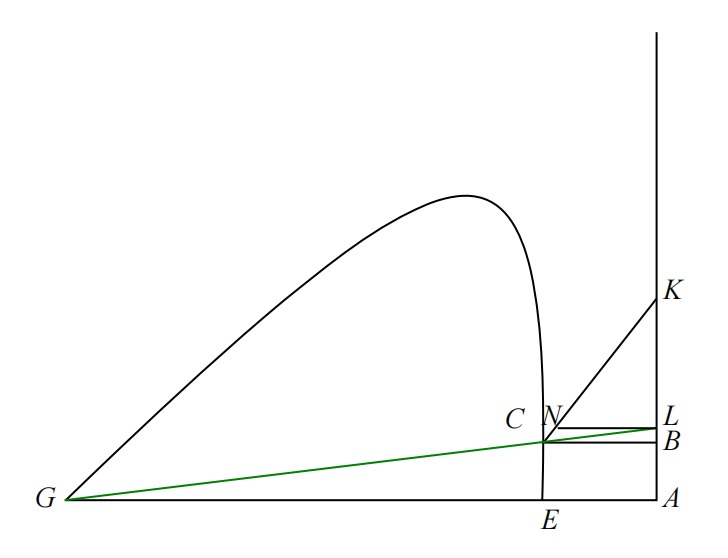
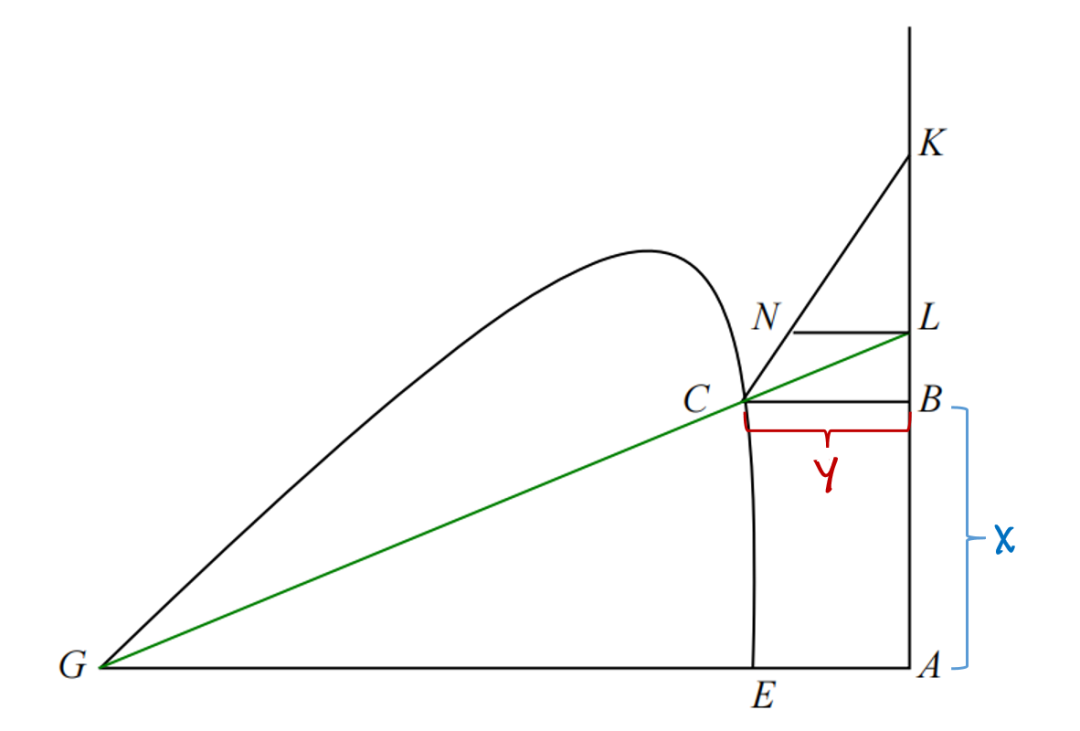
這里設(shè) 是由直尺（綠色直線）和平面直線圖形的交點(diǎn)所描繪出的曲線；直線圖形的邊可朝的方向延長(zhǎng)，圖形本身以如下方式在同一平面內(nèi)移動(dòng)：其邊可沿著直線移動(dòng)，直尺可以繞轉(zhuǎn)動(dòng)，該直尺與圖形相交于處。比如圖形往上移動(dòng)，得到，

上圖中和射線方向固定，平面圖形也給定（但邊可沿著所在直線移動(dòng)），長(zhǎng)度為，長(zhǎng)度為。

設(shè) 長(zhǎng)度 = ，長(zhǎng)度 = 。則根據(jù)相似三角形邊長(zhǎng)比例，可得和之間的關(guān)系為，

y^{2}=c y-\frac{c x}{b} y+a y-a c

根據(jù)這個(gè)方程，我們知曲線屬于第一類，實(shí)際上它是雙曲線。

若將上述解析曲線的工具中的直線圖形用平面上的雙曲線或其他第一類曲線替代，則該曲線與直尺的交點(diǎn)描繪出的將不是雙曲線，而是另一種屬于第二類的曲線。

注意，笛卡爾這里并沒(méi)有采用直角坐標(biāo)系，因?yàn)檫@里主要用到了相似三角形，并不需要兩條線相互垂直，因此實(shí)際上任意選的直線構(gòu)成的是斜角（oblique）坐標(biāo)系。況且這里水平方向的距離設(shè)為 y，另一個(gè)直線上的距離設(shè)為 x。

笛卡爾借助兩條直線（段），將曲線上的點(diǎn)與兩個(gè)數(shù)構(gòu)成的數(shù)對(duì)建立了對(duì)應(yīng)關(guān)系，即數(shù)對(duì)中兩個(gè)數(shù)滿足一個(gè)方程式。在他的思想啟發(fā)下，后人正式建立了坐標(biāo)以及坐標(biāo)系這些概念。

這里，曲線的類型與坐標(biāo)系的形式（直角或斜角）以及具體坐標(biāo)軸的選取沒(méi)有關(guān)系，可以看成曲線固有的一個(gè)屬性。當(dāng)然，得到的和肯定是跟軸的選取有關(guān)系的。這也正是與我們學(xué)習(xí)過(guò)的向量、張量具有類似的情況。

當(dāng)然，《幾何》里還有很多其他內(nèi)容，但同樣也沒(méi)有直接引入坐標(biāo)系。人家寫的書叫《方法論》，幾何只不過(guò)是附錄之一。

+小結(jié)

笛卡兒的《幾何》中雖然沒(méi)有我們現(xiàn)在所稱的笛卡兒坐標(biāo)系，即平面上的直角坐標(biāo)系，更沒(méi)有傳說(shuō)中由蜘蛛網(wǎng)想到的三維坐標(biāo)系。但他的思想和方法確實(shí)體現(xiàn)了解析幾何的精髓，也提出了坐標(biāo)系的雛形。

在笛卡爾眼中，幾何問(wèn)題不僅可歸結(jié)成為代數(shù)形式，還可通過(guò)代數(shù)變換來(lái)揭示幾何性質(zhì)。

數(shù)形結(jié)合，以形輔數(shù)，以數(shù)助形！

最后引用一句話來(lái)簡(jiǎn)單評(píng)價(jià)一下笛卡爾。《古今數(shù)學(xué)思想》的作者，數(shù)學(xué)史家克萊因評(píng)價(jià)說(shuō)：笛卡爾是近代第一位杰出的哲學(xué)家，是近代生物學(xué)的奠基人，是第一流的物理學(xué)家，但只偶然是個(gè)數(shù)學(xué)家。

偶爾為之，但卻將之前幾千年人類發(fā)展出來(lái)的幾何和代數(shù)巧妙地結(jié)合起來(lái)，并一舉點(diǎn)燃了近代數(shù)學(xué)迸發(fā)的導(dǎo)火索。

相關(guān)閱讀

什么是張量？你躺平一下就知道了

張量之對(duì)偶空間，對(duì)偶到底是個(gè)啥？