卷積神經(jīng)網(wǎng)絡(luò)(CNN)反向傳播算法推導(dǎo)

首先我給大家介紹一下我分析delta誤差反向傳播過程的簡(jiǎn)單方法，如果神經(jīng)網(wǎng)絡(luò)l+1層某個(gè)結(jié)點(diǎn)的delta誤差要傳到l層，我們就去找前向傳播時(shí)l+1層的這個(gè)結(jié)點(diǎn)和第l層的哪些結(jié)點(diǎn)有關(guān)系，權(quán)重是多少，那么反向傳播時(shí)，delta誤差就會(huì)乘上相同的權(quán)重傳播回來。

假設(shè)第l層有一個(gè)結(jié)點(diǎn)a，l+1層有一個(gè)結(jié)點(diǎn)b。兩個(gè)結(jié)點(diǎn)間的連接權(quán)重為w。如果前向傳播時(shí)，結(jié)點(diǎn)a對(duì)結(jié)點(diǎn)b的影響是 。而反向傳播時(shí)，結(jié)點(diǎn)b的delta誤差 對(duì)結(jié)點(diǎn)a的delta誤差 的影響是 。它們的系數(shù)都為兩結(jié)點(diǎn)之間的連接權(quán)重。

卷積神經(jīng)網(wǎng)絡(luò)前向傳播過程簡(jiǎn)要介紹

在理解卷積神經(jīng)網(wǎng)絡(luò)的反向傳播之前，我們需要對(duì)卷積、池化以及卷積神經(jīng)網(wǎng)絡(luò)前向傳播過程作一個(gè)簡(jiǎn)要的回顧。

卷積運(yùn)算介紹

在卷積神經(jīng)網(wǎng)絡(luò)中，所謂的卷積運(yùn)算，其實(shí)并不是嚴(yán)格的數(shù)學(xué)意義上的卷積。深度學(xué)習(xí)中的卷積實(shí)際上是信號(hào)處理和圖像處理中的互相關(guān)運(yùn)算，它們二者之間有細(xì)微的差別。深度學(xué)習(xí)中的卷積（嚴(yán)格來說是互相關(guān)）是卷積核在原始圖像上遍歷，對(duì)應(yīng)元素相乘再求和，得到的新圖像在尺寸上會(huì)有減小。可以通過下圖直觀的去理解。假設(shè)輸入圖像的有m行,n列，卷積核的尺寸為filter_size×filter_size，輸出圖像的尺寸即為(m-filter_size+1)×(n-filter_size+1)

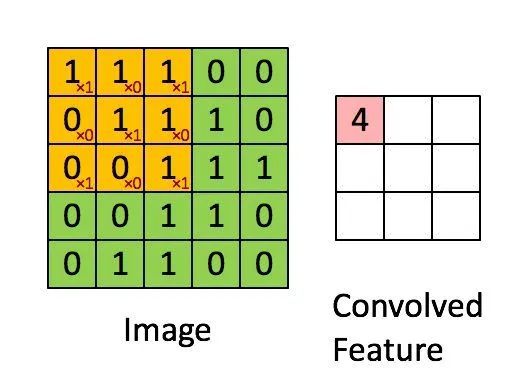
在全連接神經(jīng)網(wǎng)絡(luò)，圖像數(shù)據(jù)以及特征是以列向量的形式進(jìn)行存儲(chǔ)。而在卷積神經(jīng)網(wǎng)絡(luò)中，數(shù)據(jù)的格式主要是以張量（可以理解為多維數(shù)組）的形式存儲(chǔ)。圖片的格式為一個(gè)三維張量，行×列×通道數(shù)。卷積核的格式為一個(gè)四維張量，卷積核數(shù)×行×列×通道數(shù)。

卷積操作是每次取出卷積核中的一個(gè)，一個(gè)卷積核的格式為三維，為行×列×通道數(shù)。對(duì)應(yīng)通道序號(hào)的圖片與卷積核經(jīng)過二維卷積操作后（即上圖所示操作），得到該通道對(duì)應(yīng)的卷積結(jié)果，將所有通道的結(jié)果相加，得到輸出圖像的一個(gè)通道。每個(gè)卷積核對(duì)應(yīng)輸出圖像的一個(gè)通道，即輸出圖像的通道數(shù)等于卷積核的個(gè)數(shù)。

這里概念有一點(diǎn)繞，但是卷積神經(jīng)網(wǎng)絡(luò)中所謂張量的卷積，本質(zhì)上是進(jìn)行了一共卷積核數(shù)×通道數(shù)次二維卷積操作。每一個(gè)卷積核對(duì)應(yīng)卷積結(jié)果的一個(gè)通道，每一個(gè)卷積核的通道對(duì)應(yīng)原始圖片的一個(gè)通道。這個(gè)操作和一個(gè)列向量乘上一個(gè)矩陣得到一個(gè)新的列向量有相似的地方。

下圖直觀地展示了張量卷積具體操作過程：

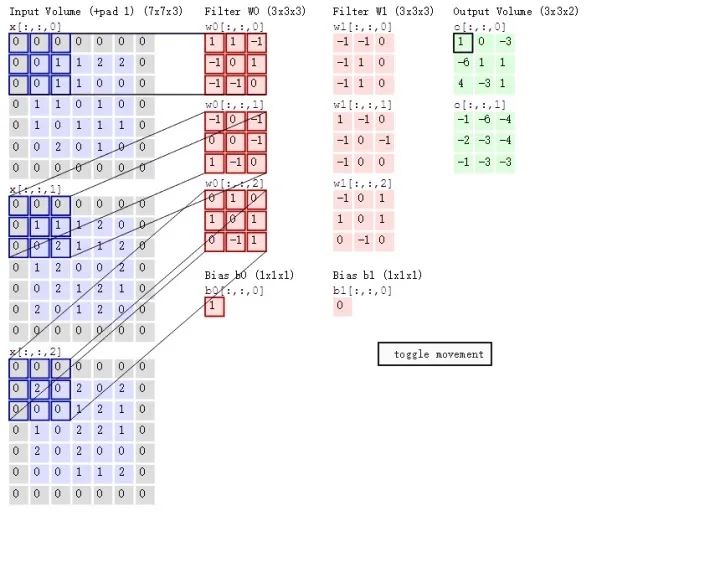
池化操作介紹

所謂的池化，就是對(duì)圖片進(jìn)行降采樣，最大池化就是在圖片中用每個(gè)區(qū)域的最大值代表這個(gè)區(qū)域，平均池化就是用每個(gè)區(qū)域平均值代表這個(gè)區(qū)域。

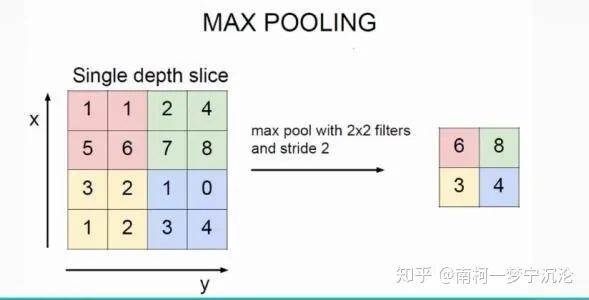
卷積神經(jīng)網(wǎng)絡(luò)反向傳播推導(dǎo)

池化層反向傳播

池化層的反向傳播比較容易理解，我們以最大池化舉例，上圖中，池化后的數(shù)字6對(duì)應(yīng)于池化前的紅色區(qū)域，實(shí)際上只有紅色區(qū)域中最大值數(shù)字6對(duì)池化后的結(jié)果有影響，權(quán)重為1，而其它的數(shù)字對(duì)池化后的結(jié)果影響都為0。假設(shè)池化后數(shù)字6的位置delta誤差為 ，誤差反向傳播回去時(shí)，紅色區(qū)域中最大值對(duì)應(yīng)的位置delta誤差即等于 ，而其它3個(gè)位置對(duì)應(yīng)的delta誤差為0。

因此，在卷積神經(jīng)網(wǎng)絡(luò)最大池化前向傳播時(shí)，不僅要記錄區(qū)域的最大值，同時(shí)也要記錄下來區(qū)域最大值的位置，方便delta誤差的反向傳播。

而平均池化就更簡(jiǎn)單了，由于平均池化時(shí)，區(qū)域中每個(gè)值對(duì)池化后結(jié)果貢獻(xiàn)的權(quán)重都為區(qū)域大小的倒數(shù)，所以delta誤差反向傳播回來時(shí)，在區(qū)域每個(gè)位置的delta誤差都為池化后delta誤差除以區(qū)域的大小。

卷積層反向傳播

雖然卷積神經(jīng)網(wǎng)絡(luò)的卷積運(yùn)算是一個(gè)三維張量的圖片和一個(gè)四維張量的卷積核進(jìn)行卷積運(yùn)算，但最核心的計(jì)算只涉及二維卷積，因此我們先從二維的卷積運(yùn)算來進(jìn)行分析：

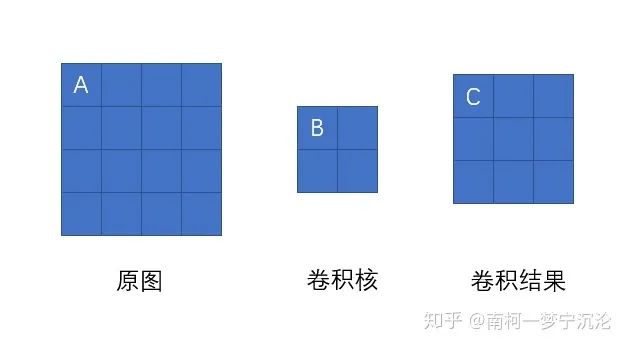
如上圖所示，我們求原圖A處的delta誤差，就先分析，它在前向傳播中影響了下一層的哪些結(jié)點(diǎn)。顯然，它只對(duì)結(jié)點(diǎn)C有一個(gè)權(quán)重為B的影響，對(duì)卷積結(jié)果中的其它結(jié)點(diǎn)沒有任何影響。因此A的delta誤差應(yīng)該等于C點(diǎn)的delta誤差乘上權(quán)重B。

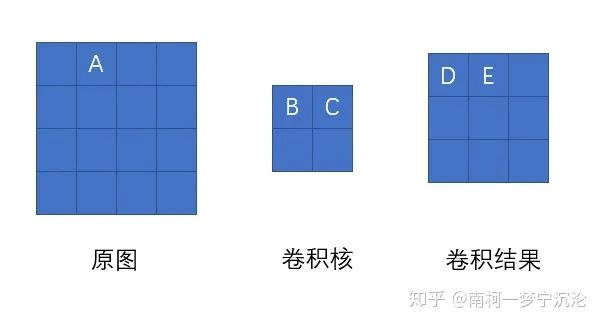
我們現(xiàn)在將原圖A點(diǎn)位置移動(dòng)一下，再看看變換位置后A點(diǎn)的delta誤差是多少，同樣先分析它前向傳播影響了卷積結(jié)果的哪些結(jié)點(diǎn)。經(jīng)過分析，A點(diǎn)以權(quán)重C影響了卷積結(jié)果的D點(diǎn)，以權(quán)重B影響了卷積結(jié)果的E點(diǎn)。那它的delta誤差就等于D點(diǎn)delta誤差乘上C加上E點(diǎn)的delta誤差乘上B。

大家可以嘗試用相同的方法去分析原圖中其它結(jié)點(diǎn)的delta誤差，結(jié)果會(huì)發(fā)現(xiàn)，原圖的delta誤差，等于卷積結(jié)果的delta誤差經(jīng)過零填充后，與卷積核旋轉(zhuǎn)180度后的卷積。如下圖所示：

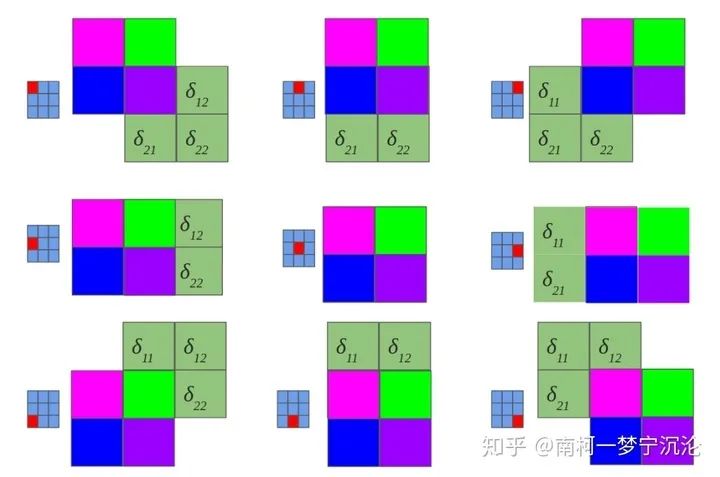
好了，直觀上的理解有了，我們接下來用數(shù)學(xué)公式來對(duì)此進(jìn)行證明，盡管它們會(huì)有些枯燥：

讓我們回顧一下delta誤差的定義，是損失函數(shù)對(duì)于當(dāng)前層未激活輸出 的導(dǎo)數(shù)，我們現(xiàn)在考慮的是二維卷積，因此，每一層的delta誤差是一個(gè)二維的矩陣。 表示的是第l層坐標(biāo)為（x,y）處的delta誤差。假設(shè)我們已經(jīng)知道第l+1層的delta誤差，利用求導(dǎo)的鏈?zhǔn)椒▌t，可以很容易寫出下式：

在這里，坐標(biāo)(x',y')是第l+1層中在前向傳播中受第l層坐標(biāo)(x,y)影響到的點(diǎn)，它們不止一個(gè)，我們需要將它們加起來。再利用前向傳播的關(guān)系式：

我們可以進(jìn)一步將表達(dá)式展開：

后面一大串盡管看起來很復(fù)雜，但實(shí)際上很容易就可以簡(jiǎn)化：

同時(shí)我們得到兩個(gè)限制條件 和

將限制條件代入上式可得：

再令 以及

我們最終的結(jié)論得到了：

我們可以短暫的慶祝一下子了，然而我們目前的結(jié)論還只是基于二維卷積，我們還需要把它推廣到我們卷積神經(jīng)網(wǎng)絡(luò)中張量的卷積中去。

再回顧一下張量的卷積，后一層的每個(gè)通道都是由前一層的各個(gè)通道經(jīng)過卷積再求和得到的。

等等，這個(gè)關(guān)系聽起來好像有點(diǎn)熟悉，如果把通道變成結(jié)點(diǎn)，把卷積變成乘上權(quán)重，這個(gè)是不是和全連接神經(jīng)網(wǎng)絡(luò)有些類似呢？

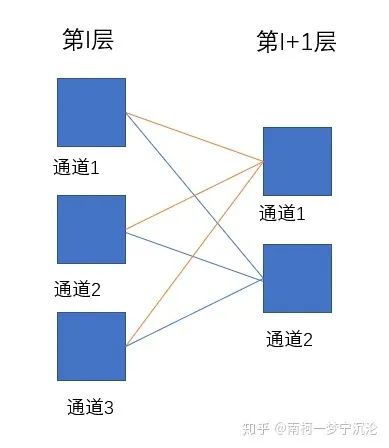
上圖中每根連線都代表與一個(gè)二維卷積核的卷積操作，假設(shè)第l層深度為3，第l+1層深度為2，卷積核的維度就應(yīng)該為2×filter_size×filter_size×3。第l層的通道1通過卷積影響了第l+1層的通道1和通道2，那么求第l層通道1的delta誤差時(shí)，就應(yīng)該根據(jù)求得的二維卷積的delta誤差傳播方式，將第l+1層通道1和通道2的delta誤差傳播到第l層的delta誤差進(jìn)行簡(jiǎn)單求和即可。

已知第l層delta誤差，求該層的參數(shù)的導(dǎo)數(shù)

,

第l層卷積核 是一個(gè)4維張量,它的維度表示為卷積核個(gè)數(shù)×行數(shù)×列數(shù)×通道數(shù)。實(shí)際上，可以把它視為有卷積核個(gè)數(shù)×通道數(shù)個(gè)二維卷積核，每個(gè)都對(duì)應(yīng)輸入圖像的對(duì)應(yīng)通道和輸出圖像的對(duì)應(yīng)通道，每一個(gè)二維卷積核只涉及到一次二維卷積運(yùn)算。那求得整個(gè)卷積核的導(dǎo)數(shù)，只需分析卷積核數(shù)×通道數(shù)次二維卷積中每個(gè)二維卷積核的導(dǎo)數(shù)，再將其組合成4維張量即可。

所以我們分析二維卷積即可：

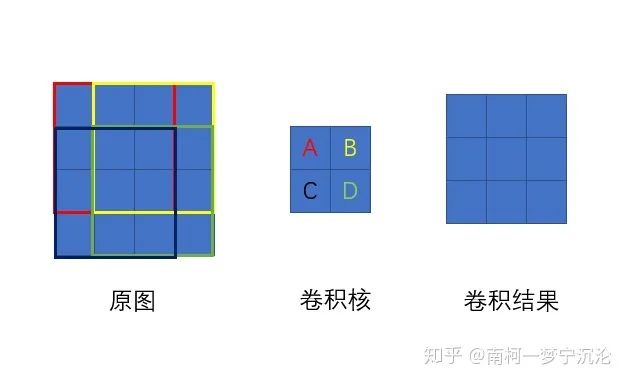
可以利用之前的分析方法，卷積核上點(diǎn)A顯然對(duì)卷積結(jié)果每一個(gè)點(diǎn)都有影響。它對(duì)卷積結(jié)果的影響等于將整個(gè)原圖左上3×3的部分乘上點(diǎn)A的值，因此delta誤差反向傳播回時(shí)，點(diǎn)A的導(dǎo)數(shù)等于卷積結(jié)果的delta誤差與原圖左上3×3紅色部分逐點(diǎn)相乘后求和。因此二維卷積核的導(dǎo)數(shù)等于原圖對(duì)應(yīng)通道與卷積結(jié)果對(duì)應(yīng)通道的delta誤差直接進(jìn)行卷積。

我們將原圖通道數(shù)×卷積結(jié)果通道數(shù)個(gè)二維卷積核的導(dǎo)數(shù)重新進(jìn)行組合成4為張量，即可得到整個(gè)卷積核的導(dǎo)數(shù)。

下面我們從數(shù)學(xué)公式進(jìn)行推導(dǎo)：

同樣我們可以進(jìn)行簡(jiǎn)化，并得到兩個(gè)限制條件： 和 :

這一次我們并不需要進(jìn)行旋轉(zhuǎn)180度這種操作。

已知第l層delta誤差，求該層的參數(shù)的導(dǎo)數(shù)

我們的 是一個(gè)列向量，它給卷積結(jié)果的每一個(gè)通道都加上同一個(gè)標(biāo)量。因此，在反向傳播時(shí)，它的導(dǎo)數(shù)等于卷積結(jié)果的delta誤差在每一個(gè)通道上將所有delta誤差進(jìn)行求和的結(jié)果。

提供簡(jiǎn)單的公式證明如下：

由于 為1

所以：

得證

卷積神經(jīng)網(wǎng)絡(luò)包括卷積層，池化層和全連接層，本文介紹了卷積層和池化層的反向傳播算法以及各層參數(shù)導(dǎo)數(shù)的計(jì)算方法，全連接層的反向傳播方法以及參數(shù)導(dǎo)數(shù)的計(jì)算在之前文章中也介紹過了。

讓我們對(duì)卷積神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程進(jìn)行一個(gè)總結(jié)：

1. 對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行初始化，定義好網(wǎng)絡(luò)結(jié)構(gòu)，設(shè)定好激活函數(shù)，對(duì)卷積層的卷積核W、偏置b進(jìn)行隨機(jī)初試化，對(duì)全連接層的權(quán)重矩陣W和偏置b進(jìn)行隨機(jī)初始化。
   設(shè)置好訓(xùn)練的最大迭代次數(shù)，每個(gè)訓(xùn)練batch的大小，學(xué)習(xí)率
2. 從訓(xùn)練數(shù)據(jù)中取出一個(gè)batch的數(shù)據(jù)
3. 從該batch數(shù)據(jù)中取出一個(gè)數(shù)據(jù)，包括輸入x以及對(duì)應(yīng)的正確標(biāo)注y
4. 將輸入x送入神經(jīng)網(wǎng)絡(luò)的輸入端，得到神經(jīng)網(wǎng)絡(luò)各層輸出參數(shù)和
5. 根據(jù)神經(jīng)網(wǎng)絡(luò)的輸出和標(biāo)注值y計(jì)算神經(jīng)網(wǎng)絡(luò)的損失函數(shù)
6. 計(jì)算損失函數(shù)對(duì)輸出層的delta誤差
7. 利用相鄰層之間delta誤差的遞推公式求得每一層的delta誤差
   如果是全連接層
   如果是卷積層
   如果是池化層
8. 利用每一層的delta誤差求出損失函數(shù)對(duì)該層參數(shù)的導(dǎo)數(shù)
   如果是全連接層：
   ，
   如果是卷積層：
   ，
9. 將求得的導(dǎo)數(shù)加到該batch數(shù)據(jù)求得的導(dǎo)數(shù)之和上(初始化為0)，跳轉(zhuǎn)到步驟3，直到該batch數(shù)據(jù)都訓(xùn)練完畢
10. 利用一個(gè)batch數(shù)據(jù)求得的導(dǎo)數(shù)之和，根據(jù)梯度下降法對(duì)參數(shù)進(jìn)行更新
    
    
11. 跳轉(zhuǎn)到步驟2，直到達(dá)到指定的迭代次數(shù)
    
    

參考：

[1]劉建平Pinard:卷積神經(jīng)網(wǎng)絡(luò)（CNN）反向傳播算法

[2]Grzegorz Gwardys:Convolutional Neural Networks backpropagation: from intuition to derivation

[3]Kunlun Bai:A Comprehensive Introduction to Different Types of Convolutions in Deep Learning

[4]CS231n Convolutional Neural Networks for Visual Recognition

推薦閱讀
13個(gè)你一定要知道的PyTorch特性
解讀：為什么要做特征歸一化/標(biāo)準(zhǔn)化？
一文搞懂 PyTorch 內(nèi)部機(jī)制
張一鳴：每個(gè)逆襲的年輕人，都具備的底層能力

關(guān)于程序員大白

程序員大白是一群哈工大，東北大學(xué)，西湖大學(xué)和上海交通大學(xué)的碩士博士運(yùn)營(yíng)維護(hù)的號(hào)，大家樂于分享高質(zhì)量文章，喜歡總結(jié)知識(shí)，歡迎關(guān)注[程序員大白]，大家一起學(xué)習(xí)進(jìn)步！