貪心算法詳解

顧名思義，貪心算法總是作出在當(dāng)前看來最好的選擇。也就是說貪心算法并不從整體最優(yōu)考慮，它所作出的選擇只是在某種意義上的局部最優(yōu)選擇。

當(dāng)然，希望貪心算法得到的最終結(jié)果也是整體最優(yōu)的。雖然貪心算法不能對所有問題都得到整體最優(yōu)解，但對許多問題它能產(chǎn)生整體最優(yōu)解。

如單源最短路經(jīng)問題，最小生成樹問題等。在一些情況下，即使貪心算法不能得到整體最優(yōu)解，其最終結(jié)果卻是最優(yōu)解的很好近似。

基本思路：

1. 建立數(shù)學(xué)模型來描述問題。
⒉.把求解的問題分成若干個子問題。
⒊.對每一子問題求解，得到子問題的局部最優(yōu)解。
⒋.把子問題的解局部最優(yōu)解合成原來解問題的一個解。

實現(xiàn)該算法的過程：

⒈.從問題的某一初始解出發(fā);
2. while 能朝給定總目標(biāo)前進(jìn)一步 do
3.求出可行解的一個解元素;
4.由所有解元素組合成問題的一個可行解。從問題的某一初始解出發(fā)


背包問題

有一個背包，最多能承載150斤的重量，現(xiàn)在有7個物品，重量分別為[35, 30, 60, 50, 40, 10, 25]，它們的價值分別為[10, 40, 30, 50, 35, 40, 30]，應(yīng)該如何選擇才能使得我們的背包背走最多價值的物品？

把物品一個個的往包里裝，要求裝入包中的物品總價值最大，要讓總價值最大，就可以想到怎么放一個個的物品才能讓總的價值最大，因此可以想到如下三種選擇物品的方法，即可能的局部最優(yōu)解：

1：每次都選擇價值最高的往包里放。
2：每次都選擇重量最小的往包里放。
3：每次都選擇單位重量價值最高的往包里放。
4：選擇價值最高的，按照制訂的規(guī)則（價值）進(jìn)行計算，順序是：4 2 6 5 。

最終的總重量是：130；最終的總價值是：165。

2：選擇重量最小的，按照制訂的規(guī)則（重量）進(jìn)行計算，順序是：6 7 2 1 5 。

最終的總重量是：140；最終的總價值是：155。可以看到，重量優(yōu)先是沒有價值優(yōu)先的策略更好。

3:選擇單位密度價值最大的，按照制訂的規(guī)則（單位密度）進(jìn)行計算，順序是：6 2 7 4 1。

最終的總重量是：150；最終的總價值是：170。

可以看到，單位密度這個策略比之前的價值策略和重量策略都要好。


單源最大路徑問題

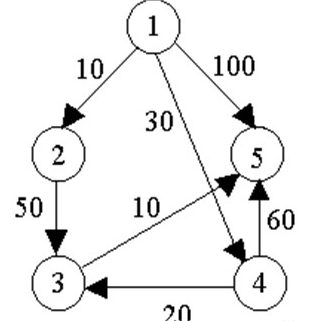
給定帶權(quán)有向圖G =(V,E)，其中每條邊的權(quán)是非負(fù)實數(shù)。另外，還給定V中的一個頂點，稱為源。現(xiàn)在要計算從源到所有其它各頂點的最短路長度。這里路的長度是指路上各邊權(quán)之和。這個問題通常稱為單源最短路徑問題。

Dijkstra算法是解單源最短路徑問題的貪心算法。

其基本思想是，設(shè)置頂點集合S并不斷地作貪心選擇來擴(kuò)充這個集合。一個頂點屬于集合S當(dāng)且僅當(dāng)從源到該頂點的最短路徑長度已知。

初始時，S中僅含有源。設(shè)u是G的某一個頂點，把從源到u且中間只經(jīng)過S中頂點的路稱為從源到u的特殊路徑，并用數(shù)組dist記錄當(dāng)前每個頂點所對應(yīng)的最短特殊路徑長度。

Dijkstra算法每次從V-S中取出具有最短特殊路長度的頂點u，將u添加到S中，同時對數(shù)組dist作必要的修改。一旦S包含了所有V中頂點，dist就記錄了從源到所有其它頂點之間的最短路徑長度。

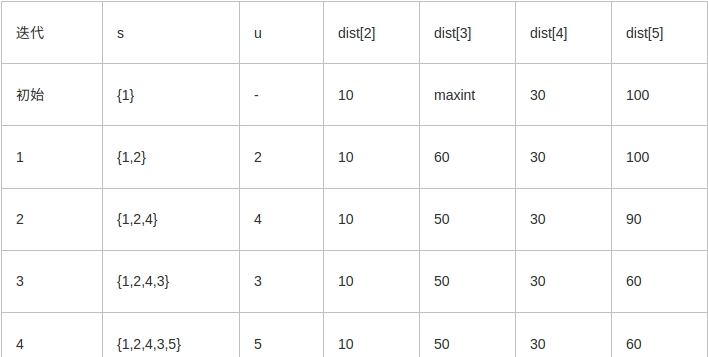
例如，對下圖中的有向圖，應(yīng)用Dijkstra算法計算從源頂點1到其它頂點間最短路徑的過程列在下表中。


Dijkstra算法的迭代過程：



算法的正確性和計算復(fù)雜性

(1)貪心選擇性質(zhì)

(2)最優(yōu)子結(jié)構(gòu)性質(zhì)

(3)計算復(fù)雜性

對于具有n個頂點和e條邊的帶權(quán)有向圖，如果用帶權(quán)鄰接矩陣表示這個圖，那么Dijkstra算法的主循環(huán)體需要O(n)時間。這個循環(huán)需要執(zhí)行n-1次，所以完成循環(huán)需要O(n)時間。算法的其余部分所需要時間不超過O(n^2)。

代碼實現(xiàn)(來自于第四個參考鏈接)：

#include #include #include using namespace std ;
class BBShortestDijkstra{public: ? ?BBShortestDijkstra (const vector<vector<int> >& vnGraph)  ? ? ? ?:m_cnMaxInt (numeric_limits<int>::max())  ? ?{ ? ? ? ?m_vnGraph = vnGraph ; ? ? ? ?m_stCount = vnGraph.size () ; ? ? ? ?m_vnDist.resize (m_stCount) ; ? ? ? ?for (size_t i = 0; i < m_stCount; ++ i) { ? ? ? ? ? ?m_vnDist[i].resize (m_stCount) ; ? ? ? ?} ? ?} ? ? ? ?void doDijkatra (){ ? ? ? ?int nMinIndex = 0 ; ? ? ? ?int nMinValue = m_cnMaxInt ; ? ? ? ?vector<bool> vbFlag (m_stCount, false) ; ? ? ? ?for (size_t i = 0; i < m_stCount; ++ i) { ? ? ? ? ? ?m_vnDist[0][i] = m_vnGraph[0][i] ; ? ? ? ? ? ?if (nMinValue > m_vnGraph[0][i]) { ? ? ? ? ? ? ? ?nMinValue = m_vnGraph[0][i] ; ? ? ? ? ? ? ? ?nMinIndex = i ; ? ? ? ? ? ?} ? ? ? ?}
 ? ? ? ?vbFlag[0] = true ; ? ? ? ?size_t k = 1 ; ? ? ? ?while (k < m_stCount) { ? ? ? ? ? ?vbFlag[nMinIndex] = true ; ? ? ? ? ? ?for (size_t j = 0; j < m_stCount ; ++ j) { ? ? ? ? ? ? ? ?// 沒有被選擇 ? ? ? ? ? ? ? ?if (!vbFlag[j] && m_vnGraph[nMinIndex][j] != m_cnMaxInt ) { ? ? ? ? ? ? ? ? ? ?if (m_vnGraph[nMinIndex][j] + nMinValue ? ? ? ? ? ? ? ? ? ? ? ?< m_vnDist[k-1][j]) { ? ? ? ? ? ? ? ? ? ? ? ?m_vnDist[k][j] = m_vnGraph[nMinIndex][j] + nMinValue ; ? ? ? ? ? ? ? ? ? ?} ? ? ? ? ? ? ? ? ? ?else { ? ? ? ? ? ? ? ? ? ? ? ?m_vnDist[k][j] = m_vnDist[k-1][j] ; ? ? ? ? ? ? ? ? ? ?} ? ? ? ? ? ? ? ?} ? ? ? ? ? ? ? ?else { ? ? ? ? ? ? ? ? ? ?m_vnDist[k][j] = m_vnDist[k-1][j] ; ? ? ? ? ? ? ? ?} ? ? ? ? ? ?} ? ? ? ? ? ?nMinValue = m_cnMaxInt ; ? ? ? ? ? ?for (size_t j = 0; j < m_stCount; ++ j) { ? ? ? ? ? ? ? ?if (!vbFlag[j] && (nMinValue > m_vnDist[k][j])) { ? ? ? ? ? ? ? ? ? ?nMinValue = m_vnDist[k][j] ; ? ? ? ? ? ? ? ? ? ?nMinIndex = j ; ? ? ? ? ? ? ? ?} ? ? ? ? ? ?} ? ? ? ? ? ?++ k ; ? ? ? ?}
 ? ? ? ?for (int i = 0; i < m_stCount; ++ i) { ? ? ? ? ? ?for (int j = 0; j < m_stCount; ++ j) { ? ? ? ? ? ? ? ?if (m_vnDist[i][j] == m_cnMaxInt) { ? ? ? ? ? ? ? ? ? ?cout << "maxint " ; ? ? ? ? ? ? ? ?} ? ? ? ? ? ? ? ?else { ? ? ? ? ? ? ? ? ? ?cout << m_vnDist[i][j] << " " ; ? ? ? ? ? ? ? ?} ? ? ? ? ? ?} ? ? ? ? ? ?cout << endl ; ? ? ? ?} ? ?}private: ? ? ?vector<vector<int> > ? ?m_vnGraph ; ? ?vector<vector<int> > ? ?m_vnDist ; ? ?size_t m_stCount ; ? ?const int m_cnMaxInt ;} ;
int main(){ ? ?const int cnCount = 5 ; ? ?vector<vector<int> > vnGraph (cnCount) ; ? ?for (int i = 0; i < cnCount; ++ i) { ? ? ? ?vnGraph[i].resize (cnCount, numeric_limits<int>::max()) ; ? ?} ? ?vnGraph[0][1] = 10 ; ? ?vnGraph[0][3] = 30 ; ? ?vnGraph[0][4] = 100 ; ? ?vnGraph[1][2] = 50 ; ? ?vnGraph[2][4] = 10 ; ? ?vnGraph[3][2] = 20 ; ? ?vnGraph[3][4] = 60 ;
 ? ?BBShortestDijkstra bbs (vnGraph) ; ? ?bbs.doDijkatra () ;}


貪心算法三個核心問題

第一個問題：為什么不直接求全局最優(yōu)解?

1.原問題復(fù)雜度過高；
2.求全局最優(yōu)解的數(shù)學(xué)模型難以建立；
3.求全局最優(yōu)解的計算量過大；
4.沒有太大必要一定要求出全局最優(yōu)解，“比較優(yōu)”就可以。

第二個問題：如何把原問題分解成子問題？

1、按串行任務(wù)分
時間串行的任務(wù)，按子任務(wù)來分解，即每一步都是在前一步的基礎(chǔ)上再選擇當(dāng)前的最優(yōu)解。

2、按規(guī)模遞減分
規(guī)模較大的復(fù)雜問題，可以借助遞歸思想（見第2課），分解成一個規(guī)模小一點點的問題，循環(huán)解決，當(dāng)最后一步的求解完成后就得到了所謂的“全局最優(yōu)解”。

3、按并行任務(wù)分
這種問題的任務(wù)不分先后，可能是并行的，可以分別求解后，再按一定的規(guī)則（比如某種配比公式）將其組合后得到最終解。

第三個問題：如何知道貪心算法結(jié)果逼近了全局最優(yōu)值？

這個問題是不能量化判斷的，正是因為全局最優(yōu)值不能夠知道，所以才求的局部最優(yōu)值。追求過程需要考慮以下幾個問題:
1.成本
耗費多少資源，花掉多少編程時間。

2.速度
計算量是否過大，計算速度能否滿足要求。

3.價值
得到了最優(yōu)解與次優(yōu)解是否真的有那么大的差別，還是說差別可以忽略。

版權(quán)聲明：本文為CSDN博主「一葉執(zhí)念」的原創(chuàng)文章，遵循CC 4.0 BY-SA版權(quán)協(xié)議，轉(zhuǎn)載請附上原文出處鏈接及本聲明。
原文鏈接：
https://blog.csdn.net/YiYeZhiNian/article/details/122211642