用 Python 機(jī)器學(xué)習(xí)預(yù)測黃金價格
本文使用機(jī)器學(xué)習(xí)方法來預(yù)測最重要的貴金屬之一黃金的價格。我們將創(chuàng)建一個線性回歸模型,該模型從過去的黃金 ETF (GLD) 價格中獲取信息,并返回對第二天黃金 ETF 價格的預(yù)測。GLD是直接投資實物黃金的最大ETF。(掃描本文最下方二維碼獲取全部完整源碼和Jupyter Notebook 文件打包下載。)
首先要做的是:導(dǎo)入所有必要庫。
#?LinearRegression?是一個用于線性回歸的機(jī)器學(xué)習(xí)庫
from?sklearn.linear_model?import?LinearRegression
#?pandas?和?numpy?用于數(shù)據(jù)操作
import?pandas?as?pd
import?numpy?as?np
#?matplotlib?和?seaborn?用于繪制圖形
import?matplotlib.pyplot?as?plt
%matplotlib?inline
plt.style.use('seaborn-darkgrid')
#?yahoo?Finance用于獲取數(shù)據(jù)
import?yfinance?as?yfdropna()?函數(shù)刪除?NaN 值。然后,我們繪制黃金 ETF 收盤價。Df?=?yf.download('GLD',?'2008-01-01',?'2020-6-22',?auto_adjust=True)
Df?=?Df[['Close']]
Df?=?Df.dropna()
Df.Close.plot(figsize=(10,?7),color='r')
plt.ylabel("Gold?ETF?Prices")
plt.title("Gold?ETF?Price?Series")
plt.show()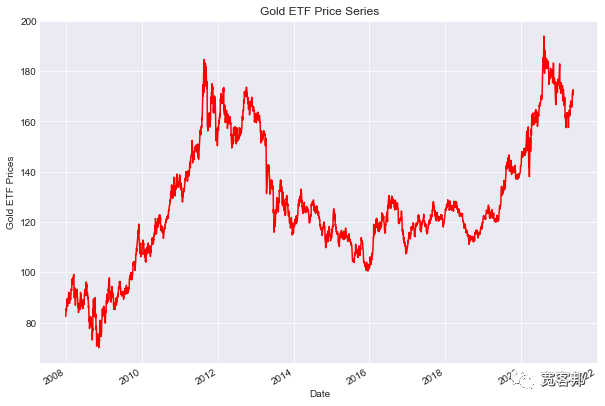
dropna() 函數(shù)刪除 NaN 值并將特征變量存儲在 X 中。Df['S_3']?=?Df['Close'].rolling(window=3).mean()
Df['S_9']?=?Df['Close'].rolling(window=9).mean()
Df['next_day_price']?=?Df['Close'].shift(-1)
Df?=?Df.dropna()
X?=?Df[['S_3',?'S_9']]
y?=?Df['next_day_price']將數(shù)據(jù)拆分為訓(xùn)練和測試數(shù)據(jù)集
在這一步中,我們將預(yù)測變量和輸出數(shù)據(jù)拆分為訓(xùn)練數(shù)據(jù)和測試數(shù)據(jù)。通過將輸入與預(yù)期輸出配對,訓(xùn)練數(shù)據(jù)用于創(chuàng)建線性回歸模型。
測試數(shù)據(jù)用于估計模型的訓(xùn)練效果。

??前 80% 的數(shù)據(jù)用于訓(xùn)練,剩余的數(shù)據(jù)用于測試
? ?X_train & y_train?是訓(xùn)練數(shù)據(jù)集
? ??X_test & y_test?是測試數(shù)據(jù)集
t?=?.8
t?=?int(t*len(Df))
X_train?=?X[:t]
y_train?=?y[:t]
X_test?=?X[t:]
y_test?=?y[t:]創(chuàng)建線性回歸模型
我們現(xiàn)在將創(chuàng)建一個線性回歸模型。但是,什么是線性回歸?
如果我們試圖捕捉“x”和“y”變量之間的數(shù)學(xué)關(guān)系,通過對散點圖擬合一條線,“最好”根據(jù)“x”的觀察值解釋“y”的觀察值,那么這樣的方程 x 和 y 之間的關(guān)系稱為線性回歸分析。
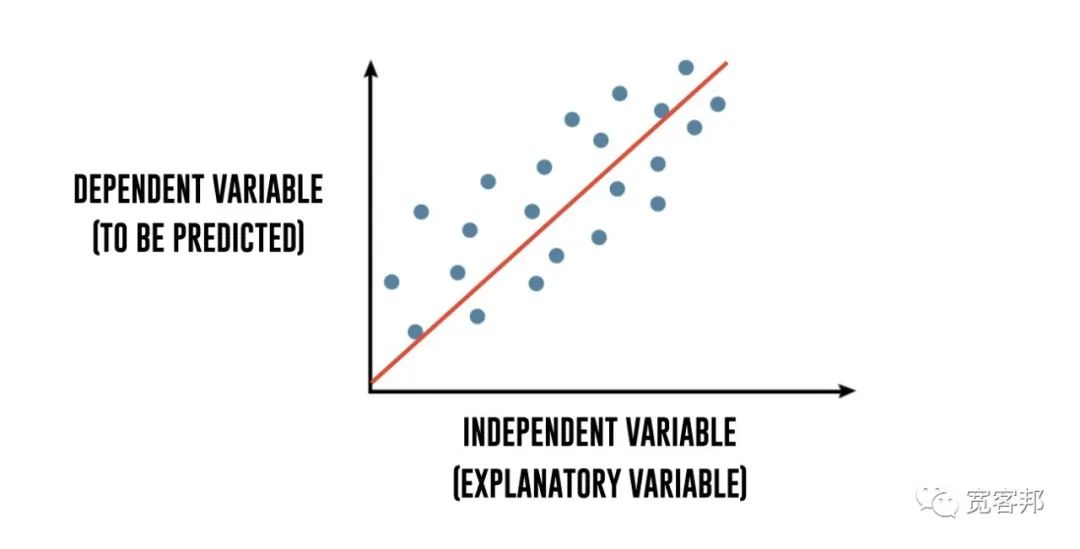
為了進(jìn)一步分解,回歸用自變量解釋了因變量的變化。因變量“y”是您要預(yù)測的變量。自變量“x”是您用來預(yù)測因變量的解釋變量。以下回歸方程描述了這種關(guān)系:
Y?=?m1?*?X1?+?m2?*?X2?+?C
Gold?ETF?price?=?m1?*?3?days?moving?average?+?m2?*?15?days?moving?average?+?c然后我們使用擬合方法擬合自變量和因變量(x 和 y)以生成回歸系數(shù)和常數(shù)。
linear?=?LinearRegression().fit(X_train,?y_train)
print("Linear?Regression?model")
print("Gold?ETF?Price?(y)?=?%.2f?*?3?Days?Moving?Average?(x1)?\
+?%.2f?*?9?Days?Moving?Average?(x2)?\
+?%.2f?(constant)"?%?(linear.coef_[0],?linear.coef_[1],?linear.intercept_))predicted_price?=?linear.predict(X_test)
predicted_price?=?pd.DataFrame(
????predicted_price,?index=y_test.index,?columns=['price'])
predicted_price.plot(figsize=(10,?7))
y_test.plot()
plt.legend(['predicted_price',?'actual_price'])
plt.ylabel("Gold?ETF?Price")
plt.show()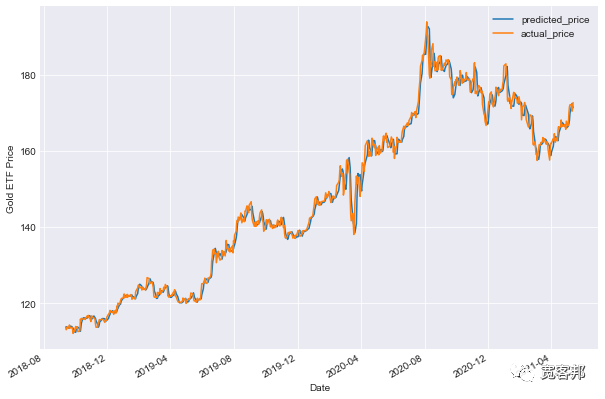
該圖顯示了黃金 ETF 的預(yù)測價格和實際價格。
現(xiàn)在,讓我們使用?score() 函數(shù)計算擬合優(yōu)度。
r2_score?=?linear.score(X[t:],?y[t:])*100
float("{0:.2f}".format(r2_score))gold?=?pd.DataFrame()
gold['price']?=?Df[t:]['Close']
gold['predicted_price_next_day']?=?predicted_price
gold['actual_price_next_day']?=?y_test
gold['gold_returns']?=?gold['price'].pct_change().shift(-1)
gold['signal']?=?np.where(gold.predicted_price_next_day.shift(1)?
gold['strategy_returns']?=?gold.signal?*?gold['gold_returns']
((gold['strategy_returns']+1).cumprod()).plot(figsize=(10,7),color='g')
plt.ylabel('Cumulative?Returns')
plt.show()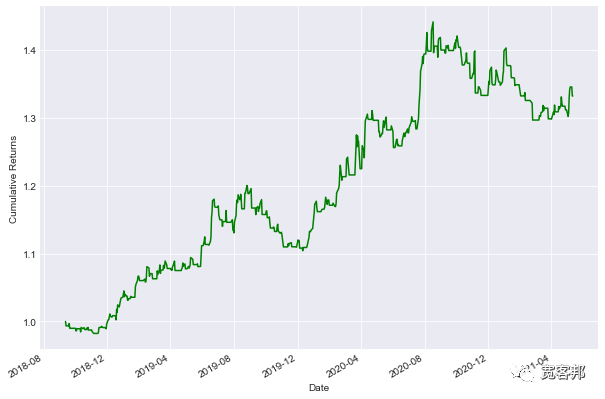
sharpe?=?gold['strategy_returns'].mean()/gold['strategy_returns'].std()*(252**0.5)
'Sharpe?Ratio?%.2f'?%?(sharpe)輸出如下:
'Sharpe Ratio 1.06'
預(yù)測每日價格
您可以使用以下代碼來預(yù)測黃金價格,并給出我們應(yīng)該購買 GLD 還是不持倉的交易信號:
import?datetime?as?dt
current_date?=?dt.datetime.now()
data?=?yf.download('GLD',?'2008-06-01',?current_date,?auto_adjust=True)
data['S_3']?=?data['Close'].rolling(window=3).mean()
data['S_9']?=?data['Close'].rolling(window=9).mean()
data?=?data.dropna()
data['predicted_gold_price']?=?linear.predict(data[['S_3',?'S_9']])
data['signal']?=?np.where(data.predicted_gold_price.shift(1)?
data.tail(1)[['signal','predicted_gold_price']].T輸出如下:


E?N?D

掃描本文最下方二維碼獲取全部完整源碼打包下載。
↓↓長按掃碼獲取完整源碼↓↓
