一看就懂 ! 圖解歸并排序
大家好,我是bigsai,我們今天來(lái)談?wù)剼w并排序算法。
歸并排序(Merge Sort)是建立在歸并操作上的一種有效,穩(wěn)定的排序算法,該算法是采用分治法(Divide and Conquer)的一個(gè)非常典型的應(yīng)用。
一、算法思想
歸并排序的主要思想是分治法。主要過(guò)程是:
1. 將n個(gè)元素從中間切開(kāi),分成兩部分。
2. 將剩下的數(shù)組通過(guò)遞歸的方式一直分割,直到數(shù)組的大小為 1,此時(shí)只有一個(gè)元素,那么該數(shù)組就是有序的了。
3. 從最底層開(kāi)始逐步合并兩個(gè)排好序的數(shù)列。把兩個(gè)數(shù)組大小為1的合并成一個(gè)大小為2的有序數(shù)列,再把兩個(gè)大小為2有序數(shù)列的合并成4的有序數(shù)列?…?直到全部小的數(shù)組合并起來(lái)。
二、思考
那么如何將兩個(gè)有序數(shù)列合成一個(gè)有序的數(shù)列呢?
我們舉個(gè)栗子把,一看就懂啦

 。
。
三、舉個(gè)栗子
例如有數(shù)組?arr [3,7,8,10,2,4,6,9]; 我們可以把這個(gè)數(shù)組分成兩個(gè)有序的子序列。分別為 [3, 7, 8, 10] 和 [2, 4, 6, 9],并將其合并為有序序列[2,3,4,6,7,8,9,10]。
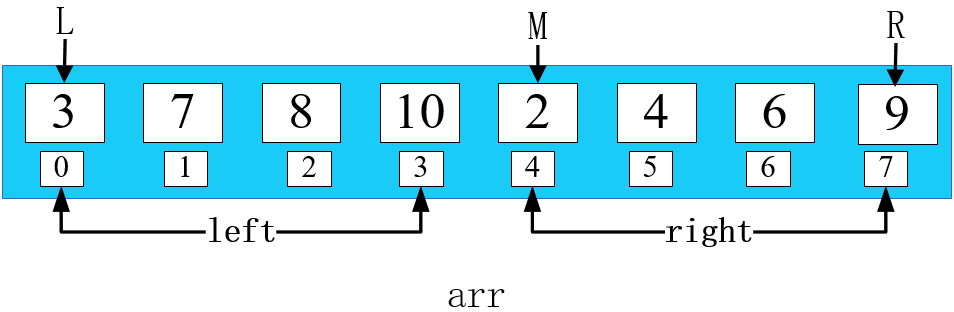
第一步:
把這兩個(gè)小的數(shù)組拆分為 left 數(shù)組和 right 數(shù)組。如下圖所示,使用 i 指向 left 的第一個(gè)元素, 使用 j 指向 right 的第一個(gè)元素。
??????????????
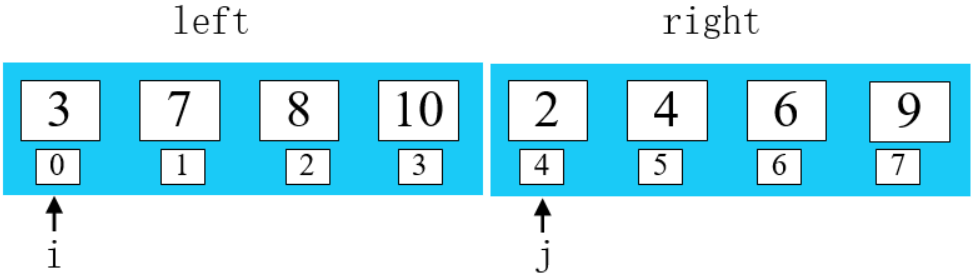
第二步:
建立一個(gè)空數(shù)組 arr ,使用 k 指向數(shù)組第一個(gè)元素。
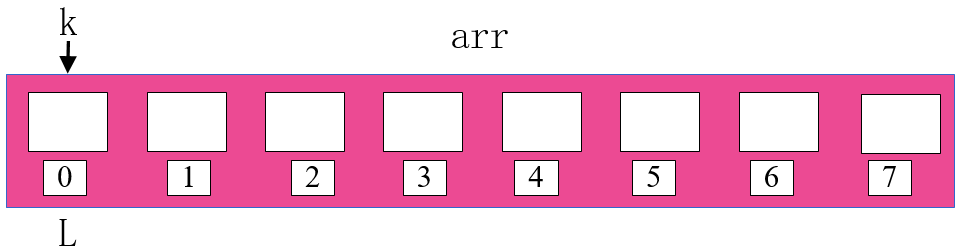
比較 i 和 j 所指數(shù)字,將小的數(shù)字放在 k 所指位置。同時(shí)將小的數(shù)字所指位置和 k 所指位置向右移一位。
2 < 3 , 將 2 填入 arr 數(shù)組 ,同時(shí)右移 j 和 k。
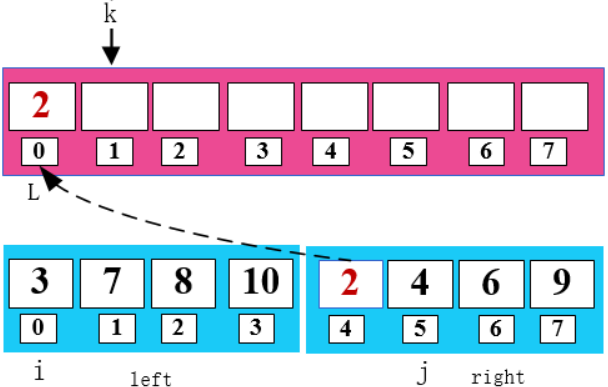
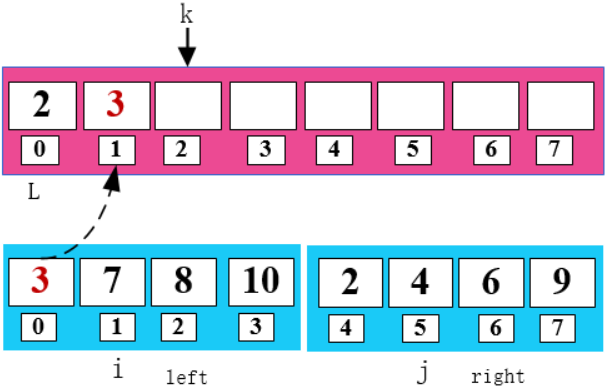
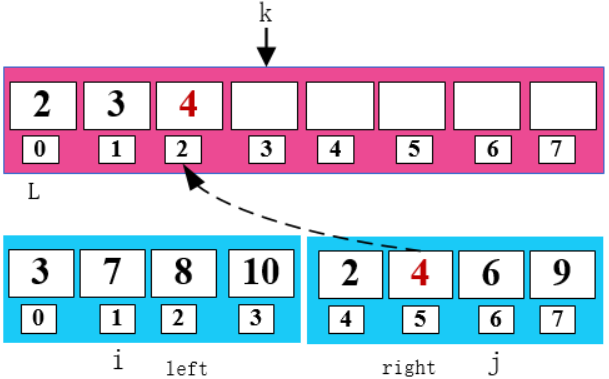
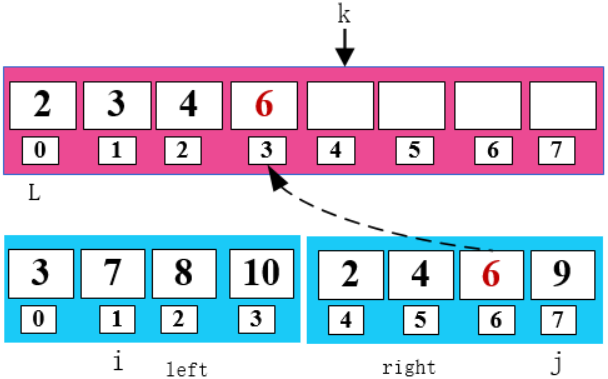
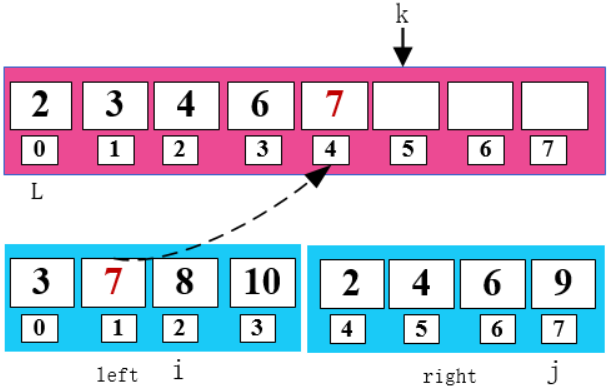
8 < 9,將 8 填入 arr 數(shù)組,同時(shí)右移 i 和 k。
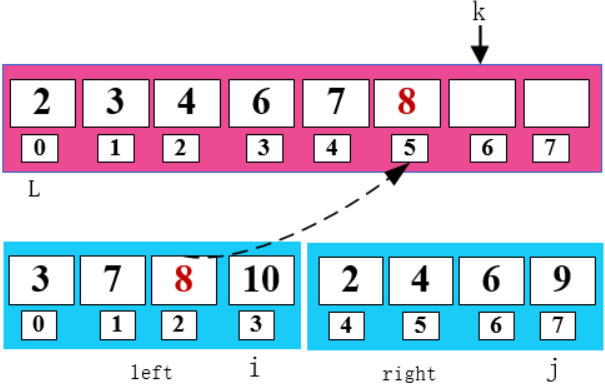
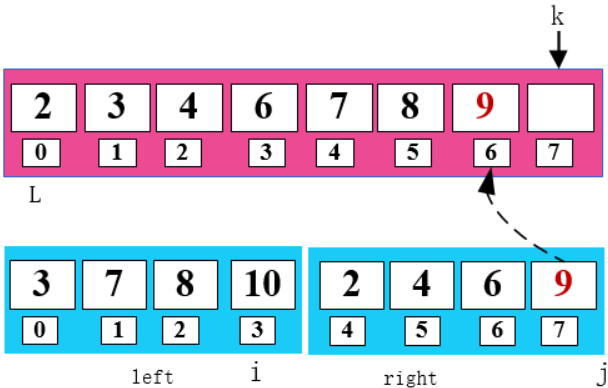
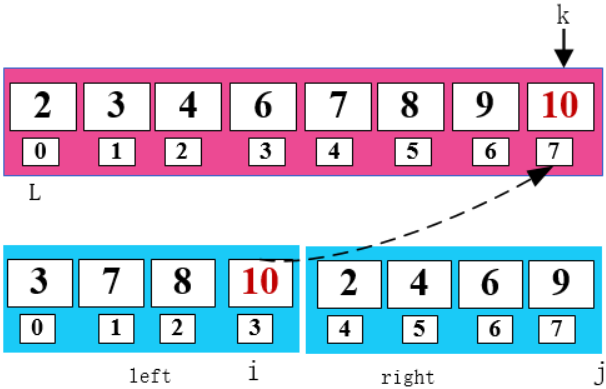
一頓操作猛如虎,這樣就把兩個(gè)有序的數(shù)組通過(guò)歸并的方式排好順序啦,是不是很贊。
那么問(wèn)題來(lái)了,難道歸并排序只能排這種有序的數(shù)組么?
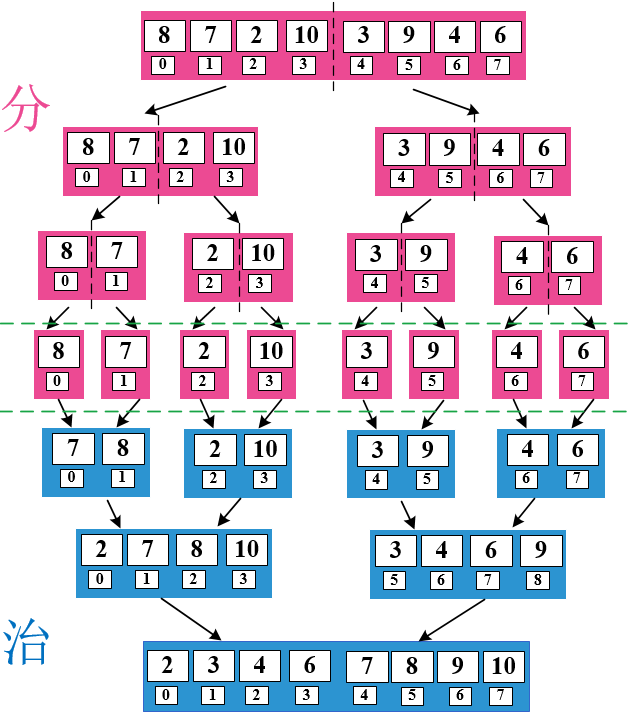
那出現(xiàn)一個(gè)無(wú)序的數(shù)組該咋辦呢?例如這個(gè)數(shù)組現(xiàn)在變?yōu)?arr [8,7,2,10,3,9,4,6];
四、問(wèn)題解決
此刻需要運(yùn)用分治(divide-and-conquer)策略(分治法將問(wèn)題分(divide)成一些小的問(wèn)題然后遞歸求解,而治(conquer)的階段則將分的階段得到的各答案"修補(bǔ)"在一起,即分而治之)。其實(shí)上面第三部分就是治(conquer)的過(guò)程,將兩個(gè)有序的序列合成為一個(gè)有序的序列。
小栗子:圖解無(wú)序序列進(jìn)行希爾排序。
五、算法實(shí)現(xiàn)
#include?
void?merge(int?arr[], int?L, int?M, int?R)?{
??int?LEFT_SIZE = M - L;
??int?RIGHT_SIZE = R - M + 1;
??int?left[LEFT_SIZE];
??int?right[RIGHT_SIZE];
??int?i, j, k;
??
??// 填充左邊的數(shù)組
???for?(i=L; i
???}
???
??// 填充右邊的數(shù)組
???for?(i=M; i<=R; i++){
?????right[i-M] = arr[i];
???}
???
// for (int i=0; i
// printf("%d\n",left[i]);
// }
//
// for (int i=0; i
// printf("%d\n",right[i]);
// }
??// 合并數(shù)組
???i = 0; j = 0; k = L;
???while?(i < LEFT_SIZE && j < RIGHT_SIZE){
?????if?(left[i] < right[j]){
???????arr[k] = left[i];
???????i++;
???????k++;
?????}else{
???????arr[k] = right[j];
???????j++;
???????k++;
?????}
???}
???
???while(i < LEFT_SIZE){
?????arr[k] = left[i];
?????i++;
?????k++;
???}
???while(j < RIGHT_SIZE){
?????arr[k] = right[j];
?????j++;
?????k++;
???}
???
}
void?mergeSort(int?arr[], int?L, int?R){
??if?(L == R){
????return;
??}else{
????int?M = (L + R) / 2;
????mergeSort(arr,L,M);
????mergeSort(arr, M+1,R);
????merge(arr, L, M+1,R);
??}
}
int?main(){
// int arr[] = {3,7,8,10,2,4,6,9};
??int?arr[] = {8,7,2,10,3,9,4,6};
??int?L = 0;
??int?M = 4;
??int?R = 7;
??mergeSort(arr,L,R);
??
??for?(int?i=0; i<=R; i++){
????printf("%d\n",arr[i]);
??}
}
六、算法分析
時(shí)間復(fù)雜度:O(nlogn)。空間復(fù)雜度:O(N),歸并排序需要一個(gè)與原數(shù)組相同長(zhǎng)度的數(shù)組做輔助來(lái)排序。
穩(wěn)定性:穩(wěn)定,因?yàn)榻粨Q元素時(shí),可以在相等的情況下做出不移動(dòng)的限制,所以歸并排序是可以穩(wěn)定的。
七、適用場(chǎng)景
歸并排序需要一個(gè)跟待排序數(shù)組同等空間的臨時(shí)數(shù)組,因此,使用歸并排序時(shí)需要考慮是否有空間上的限制。如果沒(méi)有空間上的限制,歸并排序是一個(gè)不錯(cuò)的選擇。 關(guān)注下方公眾號(hào),分享硬核知識(shí)
關(guān)注下方公眾號(hào),分享硬核知識(shí)