7分鐘搞懂邏輯回歸的來龍去脈

功能
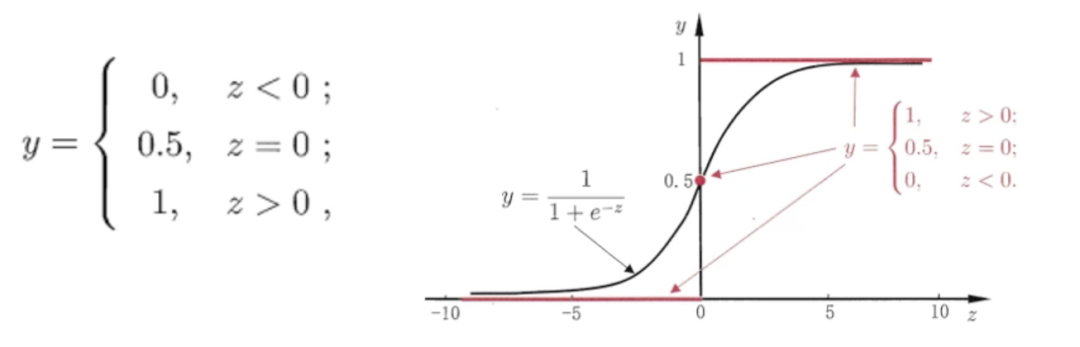
為何不叫邏輯分類?
核心問題

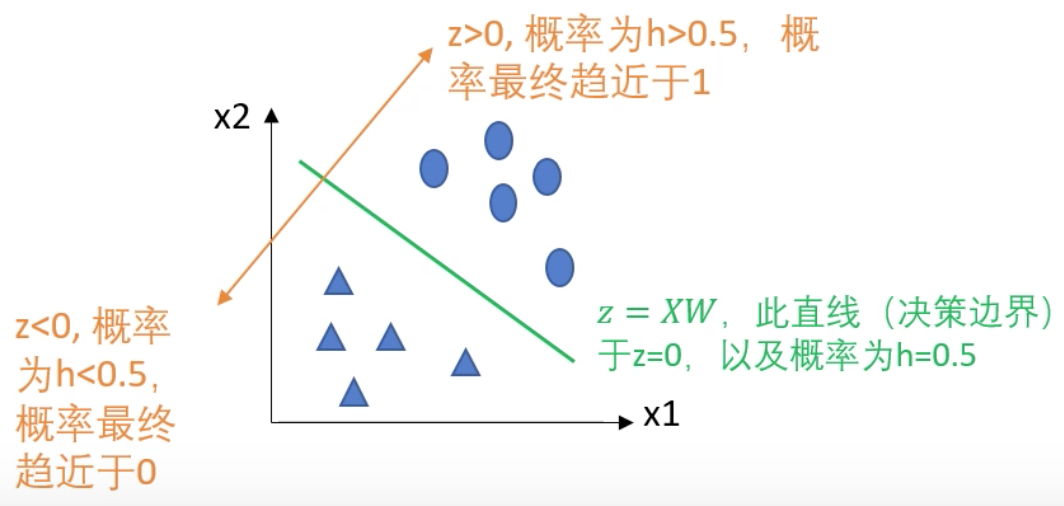
求解邊界
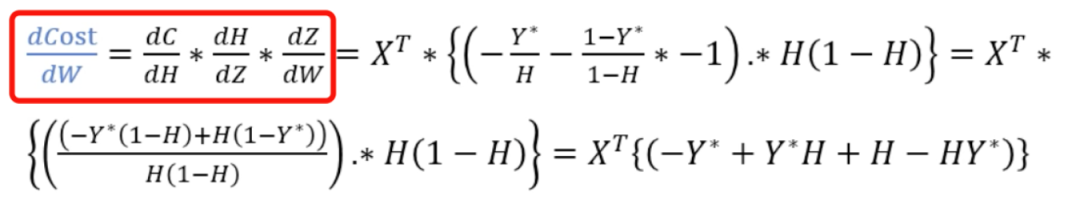
梯度下降法
初始化? ? 更新? ?:? ? 迭代到一定次數或閾值,結束



參 考 文 獻
歡? 迎? 關? 注 ??
原創(chuàng)不易,有收獲的話請幫忙點擊分享、點贊、在看吧??
評論
圖片
表情
<b id="afajh"><abbr id="afajh"></abbr></b>
 下載APP
下載APP



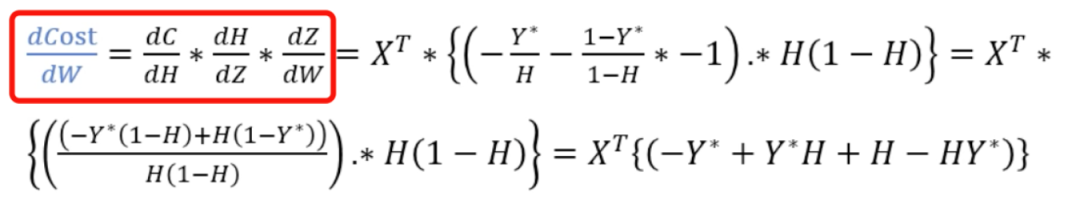



原創(chuàng)不易,有收獲的話請幫忙點擊分享、點贊、在看吧??
<b id="afajh"><abbr id="afajh"></abbr></b>