數(shù)據(jù)可視化｜用帕累托圖進行數(shù)據(jù)分析

01

你好，我是每天都想學點新東西的林驥。

1897 年，意大利經(jīng)濟學家帕累托，在抽樣調(diào)查的數(shù)據(jù)中發(fā)現(xiàn)，社會上 20% 的人擁有 80% 的財富。

后來，人們發(fā)現(xiàn)這種「關(guān)鍵少數(shù)」的現(xiàn)象非常普遍，比如說：20% 的原因?qū)е?80% 的問題，20% 的產(chǎn)品貢獻 80% 的業(yè)績，20% 的員工貢獻 80% 的業(yè)績，20% 的客戶貢獻 80% 的業(yè)績 …… 因此，簡稱為「二八法則」。

為了紀念帕累托，我們把展現(xiàn)「二八法則」的圖表，稱之為帕累托圖。

下面舉個例子，我們匯總導致質(zhì)量問題的原因，計算每種原因出現(xiàn)的頻次，然后按照從大到小進行排列，制作成一張帕累托圖如下：

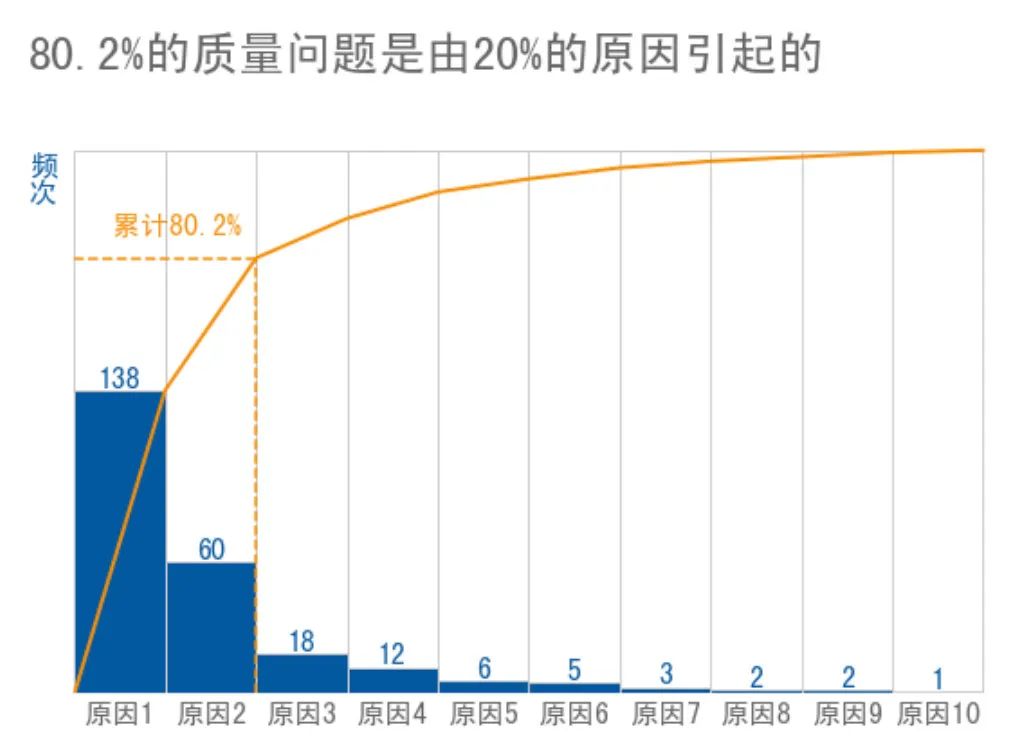
與常見的帕累托圖不同，我對圖表細節(jié)做了一些調(diào)整：

（1）線條從坐標原點開始，代表累計百分比從 0 開始；

（2）沒有使用雙坐標軸，線條的高度就是頻次的累計；

（3）灰色邊框的高度就是頻次的總和，以便展現(xiàn)部分與整體之間的占比關(guān)系；

（4）用虛線標記大致符合「二八法則」的位置；

（5）用文字標簽說明累計百分比的具體數(shù)字，在標題中體現(xiàn)圖表想要傳遞的信息。

借助帕累托圖，有助于我們抓住問題的關(guān)鍵，從而解決核心的問題。

02

接下來，我們看看用 matplotlib 畫圖的具體步驟。

首先，導入所需的庫，并設置中文字體和定義顏色等。

#?導入所需的庫
import?numpy?as?np
import?pandas?as?pd
import?matplotlib?as?mpl
import?matplotlib.pyplot?as?plt
import?matplotlib.image?as?image

#?正常顯示中文標簽
mpl.rcParams['font.sans-serif']?=?['SimHei']

#?自動適應布局
mpl.rcParams.update({'figure.autolayout':?True})

#?正常顯示負號
mpl.rcParams['axes.unicode_minus']?=?False

#?禁用科學計數(shù)法
pd.set_option('display.float_format',?lambda?x:?'%.2f'?%?x)?

#?定義顏色，主色：藍色，輔助色：灰色，互補色：橙色
c?=?{'藍色':'#00589F',?'深藍色':'#003867',?'淺藍色':'#5D9BCF',
?????'灰色':'#999999',?'深灰色':'#666666',?'淺灰色':'#CCCCCC',
?????'橙色':'#F68F00',?'深橙色':'#A05D00',?'淺橙色':'#FBC171'}

其次，從 Excel 文件中讀取數(shù)據(jù)，并定義畫圖用的數(shù)據(jù)。

#?數(shù)據(jù)源路徑
filepath='./data/帕累托圖數(shù)據(jù)源.xlsx'

#?讀取?Excel文件
df?=?pd.read_excel(filepath)

#?定義畫圖所需的數(shù)據(jù)
x?=?df['原因']
y?=?df['頻次']

#?讓折線圖從坐標原點開始
x2?=?np.arange(len(x)+1)?-?0.5
#?計算累計頻次
y_cumsum?=?[0]?+?list(y.cumsum())
#?計算累計百分比
y2?=?y.cumsum()/y.sum()

接下來，開始用「面向?qū)ο蟆沟姆椒ㄟM行畫圖。

#?使用「面向?qū)ο蟆沟姆椒ó媹D
fig,?ax?=?plt.subplots(figsize=(8,?6))

#?設置標題
ax.set_title('\n%.1f%%'?%?(y_cumsum[2]/y.sum()*100)?+?'的質(zhì)量問題是由20%的原因引起的\n',?
?????????????fontsize=26,?loc='left',?color=c['深灰色'])

#?用灰色方框代表總體的大小，體現(xiàn)每個數(shù)據(jù)的占比關(guān)系
ax.bar(x,?y.sum(),?width=1,?color='w',?edgecolor=c['淺灰色'],?zorder=0)

#?畫柱形圖
ax.bar(x,?y,?width=1,?color=c['藍色'],?edgecolor=c['淺灰色'],?zorder=1)

#?畫折線圖
ax.plot(x2,?y_cumsum,?ls='-',?lw=2,?color=c['橙色'],?label='累計百分比',?zorder=2)

#?標記體現(xiàn)二八法則的虛線
ax.hlines(y_cumsum[2],?-0.5,?1.5,?color=c['橙色'],?ls='--')
ax.vlines(1.5,?0,?y_cumsum[2],?color=c['橙色'],?ls='--')

#?隱藏邊框
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['left'].set_visible(False)

#?設置圖形的位置，減少空白
ax.spines['left'].set_position(('data',?-0.51))

#?隱藏?X?軸的刻度線
ax.tick_params(axis='x',?which='major',?length=0)
ax.tick_params(axis='y',?which='major',?length=0)
ax.set_yticklabels([])

#?設置坐標標簽字體大小和顏色
ax.tick_params(labelsize=16,?colors=c['深灰色'])

#?設置數(shù)據(jù)標簽
for?a,?a2,?b,?b2,?b3?in?zip(x,?x2[1:],?y,?y_cumsum[1:],?y2):
????ax.text(a,?b,?'%.0f'?%?b,?ha='center',?va=?'bottom',?fontsize=16,?color=c['藍色'])
????

#?標記?Y?軸標題
ax.text(-1,?y.sum(),?'頻\n次',?fontsize=16,?va='top',?color=c['藍色'])

#?標記線條含義
ax.text(1.5,?y_cumsum[2]+10,?'累計%.1f%%?'?%?(y_cumsum[2]/y.sum()*100),?fontsize=16,?color=c['橙色'],?va='bottom',?ha='right',?zorder=5)

plt.show()

你可以前往 https://github.com/linjiwx/mp 下載畫圖用的數(shù)據(jù)和完整代碼。

03

通過廣泛尋找問題的原因，會發(fā)現(xiàn)影響因素有很多，但是各種因素對問題的影響程度并不相同，因此需要縮小范圍，找出導致問題的主要原因。

要識別問題的主要原因，可以借助帕累托圖，對各種原因進行優(yōu)先級排序，多問幾個「為什么」，逐級分析，以確定根本原因。

1951 年，管理學家戴克將帕累托圖應用于庫存管理，命名為 ABC 分析法。

1963 年，德魯克將 ABC 分析法進一步推廣，使其成為企業(yè)提高效益的管理方法。

對于個人來講，我把自己的工作清單分成 3 大類：

A 類：需要投入巨大精力的長期工作。

B 類：需要及時響應并完成的工作。

C 類：需要快速跟進處理的工作。

堅持「要事優(yōu)先」的原則，每天分配時間給重要的事情，我認為這也算是「二八法則」的一種實際應用。