小电影在线观看黄.999,黄色强奸免费小视频网站,毛片黄片一机片,亚洲欧美怡红院,找个免费的a片,一道本激情视频,在线观看视频你懂的,偷拍视频hd

伴隨矩陣（Adjoint matrix），這個(gè)名詞是 Maxime B?cher 在 1907 年出版的《Introduction to Higher Algebra》中首次引入的。

也就是說(shuō)并不像是誰(shuí)直接提出這個(gè)概念的，那它大概怎么來(lái)的呢？根據(jù)一些歷史資料及本人大膽推測(cè)，大致是由行列式，到拉普拉斯展開(kāi)式，再到伴隨矩陣，這么個(gè)路徑。但這期間可能還涉及高斯的工作，這部分內(nèi)容放在本文后面部分。

1Laplace 展開(kāi)式

行列式的英文單詞是 determinant，是決定因素或者決定性的的意思。那它到底是要決定什么呢？

行列式最初定義為線性方程組的一個(gè)屬性，它決定了該線性方程組是否具有唯一解，即如果行列式不等于零，則方程組有唯一解。如果行列式等于零，則方程組有無(wú)窮多組解或者無(wú)解。

后來(lái)隨著矩陣概念的誕生，行列式能夠用來(lái)表征矩陣以及由矩陣表示的線性映射的一些屬性。特別地，當(dāng)且僅當(dāng)矩陣可逆且矩陣表示的線性映射是同構(gòu)時(shí)，行列式是非零的。

不過(guò)本文主要看行列式的定義與計(jì)算。

+行列式的定義

對(duì)于矩陣，它的行列式定義為，

\operatorname{det}({A})=\sum_{p} \sigma(p) a_{1 p_{1}} a_{2 p_{2}} \cdots a_{n p_{n}}

其中，總和取于的個(gè)置換，而是置換的符號(hào)（奇偶性）。

我們都知道，當(dāng)矩陣階數(shù)為和時(shí)可以按如下方式展開(kāi)來(lái)計(jì)算行列式。

+n = 2 時(shí)

\begin{gathered} A=\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right] \\[2em] \operatorname{det}[{A}]=+A_{11} \cdot \operatorname{det}\left[A_{22}\right]-A_{12} \cdot \operatorname{det}\left[A_{21}\right]=A_{11} A_{22}-A_{21} A_{21} \end{gathered}

+n = 3 時(shí)

A=\left[\begin{array}{lll} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{array}\right]

按第行展開(kāi)，

\begin{aligned} \operatorname{det}[A] &=+A_{11} \cdot \operatorname{det}\left[\begin{array}{ll} A_{22} & A_{23} \\ A_{32} & A_{33} \end{array}\right]-A_{12} \cdot \operatorname{det}\left[\begin{array}{ll} A_{21} & A_{23} \\ A_{31} & A_{33} \end{array}\right]+A_{13} \cdot \operatorname{det}\left[\begin{array}{ll} A_{21} & A_{22} \\ A_{31} & A_{32} \end{array}\right] \\[1.5em] &=+A_{11}\left(A_{22} A_{33}-A_{23} A_{32}\right)-A_{12}\left(A_{21} A_{33}-A_{23} A_{31}\right)+A_{13}\left(A_{21} A_{32}-A_{22} A_{31}\right) \\[2em] &=+A_{11} A_{22} A_{33}+A_{12} A_{23} A_{31}+A_{13} A_{21} A_{32}-A_{11} A_{23} A_{32}-A_{12} A_{21} A_{33}-A_{13} A_{22} A_{31} \end{aligned}

此處可以插入一個(gè)圖，更形象地展示上述展開(kāi)過(guò)程。

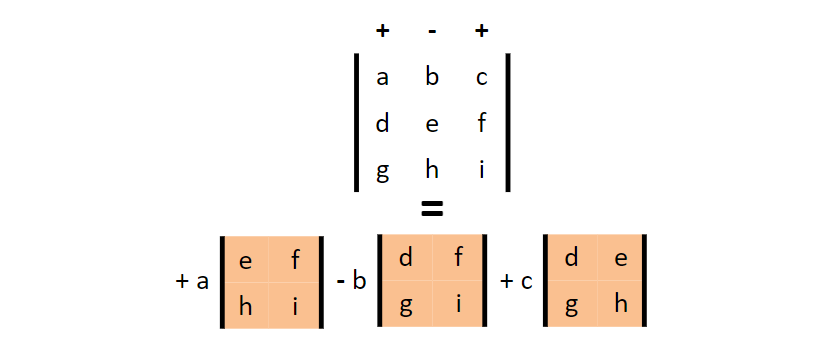
接下來(lái)就是開(kāi)啟找規(guī)律的模式，看看當(dāng)矩陣的階數(shù)升高后有沒(méi)有類(lèi)似的計(jì)算套路。

當(dāng)矩陣的階數(shù)增加上去會(huì)怎么樣呢？答案是仍然有類(lèi)似的結(jié)論，那就是 Laplace 展示式。

+Laplace 展開(kāi)式

上面的試探可以發(fā)現(xiàn)，階行列式的計(jì)算中可以用到階行列式，于是很自然地想到，可以遞歸式計(jì)算高階行列式。為了把高階行列式展開(kāi)成低階行列式來(lái)計(jì)算，有必要將其中涉及的計(jì)算模式理一理清楚，進(jìn)而引入了余子式和代數(shù)余子式這樣的概念。而 Laplace 展開(kāi)式在這些基礎(chǔ)上順勢(shì)而出了，具體形式如下

\begin{cases}\sum_{j=1}^{n} A_{i j} C_{k j}=\operatorname{det}(A) & i=k \\[1.618em] \sum_{j=1}^{n} A_{i j} C_{k j}=0 & i \neq k \end{cases}

其中是指代數(shù)余子式，即

C_{i j} = (-1)^{i+j} M_{i j}

而是元素的余子式。

Laplace 展開(kāi)式里的第一條是可以拿來(lái)遞歸式求解行列式（只是效率并不高）。值得注意的是第二條，它的意思就是只要按錯(cuò)誤的行或列（）展開(kāi)就會(huì)得到，這一點(diǎn)很容易驗(yàn)證，只要用第行代替第行，而有相同行的行列式自然就是。

這兩條要放在一起觀察，從形式上看，像不像兩個(gè)矩陣相乘的姿勢(shì)？即，而它們的積除對(duì)角線元素外全部是，而且，對(duì)角線上的元素竟然全部相等。

矩陣的對(duì)角化一直是數(shù)學(xué)家的追求，現(xiàn)在得到的不僅是對(duì)角化，甚至是單位（矩陣）化了，哪還有不歡喜的理由？

總之，我們得到了下面這個(gè)式子，

AC^{\top} = \operatorname{det}(A)I

的轉(zhuǎn)置矩陣就稱(chēng)為的伴隨矩陣，從形式上看伴隨矩陣就很有逆矩陣的樣子了，當(dāng) 可逆時(shí)就可以用來(lái)計(jì)算它的逆矩陣。于是，便得到下面的命題。

命題令為的矩陣，是它的伴隨（adjoint）矩陣，則有，

A\;\!\operatorname{adj}(A)=\operatorname{adj}(A)\;\! A=\operatorname{det}(A)\;\! I

其中，是階單位矩陣。

我們來(lái)看一下當(dāng) 時(shí)的情況，

\begin{aligned} &\operatorname{adj}(A)=C^{\top}=\\[1em] &\left[\begin{array}{l} +\left|\begin{array}{ll} A_{22} & A_{23} \\ A_{32} & A_{33} \end{array}\right|\;-\left|\begin{array}{ll} A_{12} & A_{13} \\ A_{32} & A_{33} \end{array}\right|\;+\left|\begin{array}{ll} A_{12} & A_{13} \\ A_{22} & A_{23} \end{array}\right| \\[1em] -\left|\begin{array}{ll} A_{21} & A_{23} \\ A_{31} & A_{33} \end{array}\right|\;+\left|\begin{array}{ll} A_{11} & A_{13} \\ A_{31} & A_{33} \end{array}\right|\;-\left|\begin{array}{ll} A_{11} & A_{13} \\ A_{21} & A_{23} \end{array}\right| \\[1em] +\left|\begin{array}{ll} A_{21} & A_{22} \\ A_{31} & A_{32} \end{array}\right|\;-\left|\begin{array}{ll} A_{11} & A_{12} \\ A_{31} & A_{32} \end{array}\right|\;+\left|\begin{array}{ll} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right|\; \end{array}\right] \end{aligned}

這里為什么不直接除以呢，讓它成為逆矩陣不是更好嗎？這樣做的一個(gè)原因應(yīng)該是可以統(tǒng)一處理，不管矩陣奇異還是非奇異。

而當(dāng)矩陣可逆時(shí)，這提供了一種逆矩陣的表示以及計(jì)算方案，估計(jì)是為了叫起來(lái)方便一些，于是給它一個(gè)名分。看它倆左右相伴，就叫做伴隨矩陣唄。

值得注意的是，這里的伴隨與伴隨算子中的伴隨沒(méi)有關(guān)系，不用去強(qiáng)行將兩者聯(lián)系起來(lái)。

這個(gè)伴隨矩陣聽(tīng)著名字挺香的，構(gòu)思也挺巧妙的，只是用處大嗎？

矩陣的一個(gè)重要用處是拿來(lái)表示線性變換，比如向量在矩陣的作用下可以變成另一個(gè)向量，那么有時(shí)候就要求能夠變回來(lái)是吧。

因此，矩陣有必要和它的另一半成雙成對(duì)出現(xiàn)，而伴隨矩陣就是差不多充當(dāng)這么個(gè)角色，它與逆矩陣也只差一個(gè)因子。

如果矩陣不可逆，即行列式為，此時(shí)我們有，

A\;\!\operatorname{adj}(A)=0

此時(shí)伴隨矩陣與齊次線性方程組的解有關(guān)。大家不妨考慮下當(dāng) 的秩為時(shí)的情況。

好了，接下來(lái)讓我們想一想，伴隨矩陣還有其他的用途嗎？

2二次型的伴隨式

我們直入主題，現(xiàn)有如下二次型，

\begin{aligned} \sum_\nolimits{1}^{n} A_{i j} x_{i} x_{j} \end{aligned}

由它可以衍生出另一個(gè)二次型，

\begin{aligned} &{\sum}_{1}^{n} C_{i j} u_{i} u_{j} \equiv-\left|\begin{array}{llll} A_{11} & \cdots & A_{1 n} & u_{1} \\ & \cdot & \cdot & \\ & \cdot & \cdot & \\ A_{n 1} & \cdots & A_{n n} & u_{n} \\ \;u_{1} & \cdots & u_{n} & 0 \end{array}\right| \end{aligned}

這是變?cè)?的二次型，其系數(shù)矩陣正是矩陣的伴隨矩陣。第二個(gè)式子稱(chēng)為第一個(gè)式子的伴隨二次型。

仔細(xì)看上面這個(gè)行列式，它將行列式、二次型以及伴隨矩陣等融合在一起，十分巧妙。

這個(gè)事情似乎跟高斯的工作有關(guān)，高斯在研究如下表示的三元二次型時(shí)，

ax^2+a'x'^2+a''x''^2+2bx'x''+2b'xx''+2b''xx'

引入了它的伴隨式子，

Ax^2+A'x'^2+A''x''^2+2Bx'x''+2B'xx''+2B''xx'

其中，

\begin{array}{lll} A=bb-a'a'',& A'=b'b'-aa'',& A''=b''b''-aa' \\[1em] B=ab-b'b'',& B'=a'b'-bb'',& B''=a''b''-bb' \end{array}

高斯在他的《算術(shù)探究》里引入上述概念，但那會(huì)兒還沒(méi)矩陣，轉(zhuǎn)化為矩陣的形式就對(duì)應(yīng)如下兩個(gè)矩陣。

\left[\begin{array}{lll} a & b'' & b' \\ b'' & a' & b \\ b' & b & a'' \\ \end{array}\right]

和

\left[\begin{array}{lll} A & B'' & B' \\ B'' & A' & B \\ B' & B & A'' \\ \end{array}\right]

這應(yīng)該是二次型伴隨式的原型，也可能是伴隨矩陣這個(gè)名詞的來(lái)源之一。

3附錄

+命題的證明

可以從元素級(jí)別暴力證明。首先如下定義一個(gè)矩陣

B=A\;\!\operatorname{adj}(A)

左右兩邊矩陣的相應(yīng)元素相等，得

\begin{aligned} & B_{i j} \\[0.6em] =& \sum_{k=1}^{n} A_{i k}[\operatorname{adj}(A)]_{k j} \\[0.6em] =& \sum_{k=1}^{n} A_{i k} C_{j k} \end{aligned}

當(dāng) 時(shí)，由的 Laplace 展開(kāi)式可得等于。當(dāng) 時(shí)，相當(dāng)于展開(kāi)式中沿著錯(cuò)誤的行展開(kāi)了，因此等于。由此可得

B=\left[\begin{array}{cccc} \operatorname{det}(A) & 0 & \cdots & 0 \\ 0 & \operatorname{det}(A) & & \vdots \\ \vdots & & \ddots & \\ 0 & \cdots & & \operatorname{det}(A) \end{array}\right]=\operatorname{det}(A)\;\! I

以及，

D =\operatorname{adj}(A) \;\!A

比較兩邊元素，得

\begin{aligned} & D_{i j} \\[0.6em] =& \sum_{k=1}^{n}[\operatorname{adj}(A)]_{i k} \;\!A_{k j} \\[0.6em] =& \sum_{k=1}^{n} A_{k j} C_{k i} \end{aligned}

這是按列展開(kāi)，跟上面類(lèi)似，得

D=\operatorname{det}(A) \;\!I

因此，如果是可逆矩陣，則它的逆矩陣為，

A^{-1}=\frac{1}{\operatorname{det}(A)} \;\!\operatorname{adj}(A)

相關(guān)閱讀

線性代數(shù)一百問(wèn)之二：伴隨矩陣這么巧妙，怎么來(lái)的？