Python實(shí)現(xiàn)經(jīng)典排序算法，再也不怕面試官讓我手寫(xiě)快排了！

大家好，歡迎來(lái)到Crossin的編程教室！

算法作為程序員的必修課，是每位程序員必須掌握的基礎(chǔ)。本篇我們將通過(guò)Python來(lái)實(shí)現(xiàn)5大經(jīng)典排序算法，結(jié)合例圖剖析內(nèi)部實(shí)現(xiàn)邏輯，對(duì)比每種算法各自的優(yōu)缺點(diǎn)和應(yīng)用點(diǎn)。相信我，耐心看完絕對(duì)有收獲。

準(zhǔn)備工作

大家都知道從理論上講，我們一般會(huì)使用大O表示法測(cè)量算法的運(yùn)行時(shí)復(fù)雜度。"大O表示法"表示程序的執(zhí)行時(shí)間或占用空間隨數(shù)據(jù)規(guī)模的增長(zhǎng)趨勢(shì)。

但為了測(cè)算具體的時(shí)間，本篇將使用timeit模塊來(lái)衡量實(shí)現(xiàn)的運(yùn)行時(shí)間。下面自己寫(xiě)一個(gè)對(duì)算法測(cè)試時(shí)間的函數(shù)。

from?random?import?randint
from?timeit?import?repeat

def?run_sorting_algorithm(algorithm,?array):
????#?調(diào)用特定的算法對(duì)提供的數(shù)組執(zhí)行。
????#?如果不是內(nèi)置sort()函數(shù)，那就只引入算法函數(shù)。
????setup_code?=?f"from?__main__?import?{algorithm}"?\
????????if?algorithm?!=?"sorted"?else?""

????stmt?=?f"{algorithm}({array})"

????#?十次執(zhí)行代碼，并返回以秒為單位的時(shí)間
????times?=?repeat(setup=setup_code,?stmt=stmt,?repeat=3,?number=10)

????#?最后，顯示算法的名稱和運(yùn)行所需的最短時(shí)間
????print(f"Algorithm:?{algorithm}.?Minimum?execution?time:?{min(times)}")

這里用到了一個(gè)騷操作，通過(guò)f-strings魔術(shù)方法導(dǎo)入了算法名稱，不懂的可以參考：Python 格式化字符串的最佳姿勢(shì)

注意：應(yīng)該找到算法每次運(yùn)行的平均時(shí)間，而不是選擇單個(gè)最短時(shí)間。由于系統(tǒng)同時(shí)運(yùn)行其他進(jìn)程，因此時(shí)間測(cè)量是受影響的。最短的時(shí)間肯定是影響最小的，是這樣才使其成為算法時(shí)間最短的。

Python中的冒泡排序算法

冒泡排序是最直接的排序算法之一。它的名稱來(lái)自算法的工作方式：每經(jīng)過(guò)一次新的遍歷，列表中最大的元素就會(huì)“冒泡”至正確位置。

在Python中實(shí)現(xiàn)冒泡排序

這是Python中冒泡排序算法的實(shí)現(xiàn)：

def?bubble_sort(array):
?????n?=?len(array)
?
?????for?i?in?range(n):
?????????#?創(chuàng)建一個(gè)標(biāo)識(shí)，當(dāng)沒(méi)有可以排序的時(shí)候就使函數(shù)終止。
?????????already_sorted?=?True
?
?????????#?從頭開(kāi)始逐個(gè)比較相鄰元素，每一次循環(huán)的總次數(shù)減1，
?????????#?因?yàn)槊看窝h(huán)一次，最后面元素的排序就確定一個(gè)。
?????????for?j?in?range(n?-?i?-?1):
?????????????if?array[j]?>?array[j?+?1]:
?????????????????#?如果此時(shí)的元素大于相鄰后一個(gè)元素，那么交換。
?????????????????array[j],?array[j?+?1]?=?array[j?+?1],?array[j]
?
?????????????????#?如果有了交換，設(shè)置already_sorted標(biāo)志為False算法不會(huì)提前停止
?????????????????already_sorted?=?False
?
?????????#?如果最后一輪沒(méi)有交換，數(shù)據(jù)已經(jīng)排序完畢，退出
?????????if?already_sorted:
?????????????break
?
?????return?array

為了正確分析算法的工作原理，看下這個(gè)列表[8, 2, 6, 4, 5]。假設(shè)使用bubble_sort()排序，下圖說(shuō)明了算法每次迭代時(shí)數(shù)組的實(shí)際換件情況：

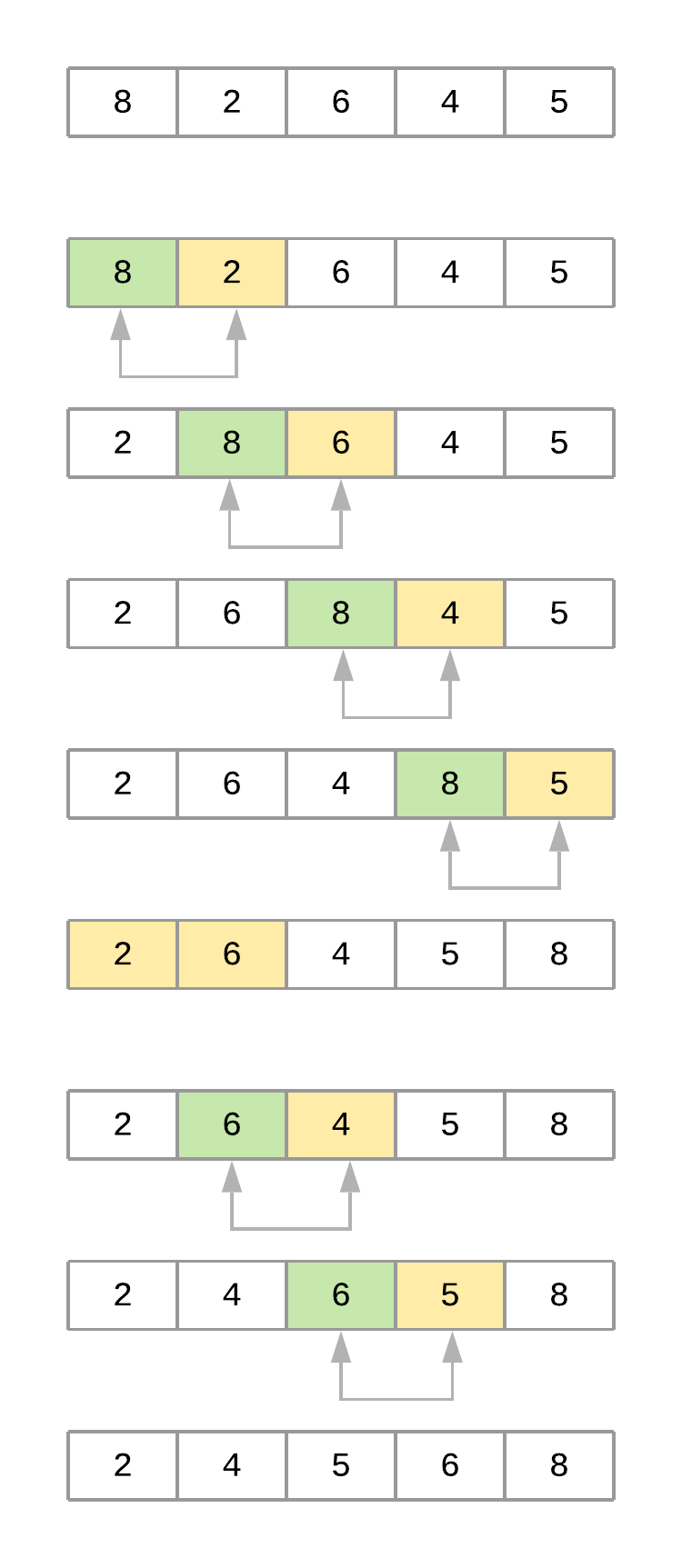
冒泡排序的實(shí)現(xiàn)由兩個(gè)嵌套for循環(huán)組成，其中算法先執(zhí)行n-1個(gè)比較，然后進(jìn)行n-2個(gè)比較，依此類推，直到完成最終比較。因此，總的比較次數(shù)為（N - 1）+（N - 2）+（N - 3）+ ... + 2 + 1 = N（N-1）/ 2，也可以寫(xiě)成 ?n?²?- ?n。

去掉不會(huì)隨數(shù)據(jù)規(guī)模n而變化的常量，可以將符號(hào)簡(jiǎn)化為 n²?-n。由于 n²的增長(zhǎng)速度快于n，因此也可以舍棄最后一項(xiàng)，使冒泡排序的平均和最壞情況下的時(shí)間復(fù)雜度為 O（n?²）。

在算法接收到已排序的數(shù)組的情況下，運(yùn)行時(shí)間復(fù)雜度將降低到更好的O（n），因?yàn)樗惴ㄑh(huán)一遍沒(méi)有任何交換，標(biāo)志是true，所以循環(huán)一遍比較了N次直接退出。因此，O（n）是冒泡排序的最佳情況運(yùn)行時(shí)間復(fù)雜度。但最好的情況是個(gè)例外，比較不同的算法時(shí)，應(yīng)該關(guān)注平均情況。

冒泡排序的時(shí)間運(yùn)行測(cè)試

使用run_sorting_algorithm()測(cè)試冒泡排序處理具有一萬(wàn)個(gè)元素的數(shù)組所花費(fèi)的時(shí)間。

ARRAY_LENGTH?=?10000if?__name__?==?"__main__":
?????#?生成包含“?ARRAY_LENGTH”個(gè)元素的數(shù)組，元素是介于0到999之間的隨機(jī)整數(shù)值
?????array?=?[randint(0,?1000)?for?i?in?range(ARRAY_LENGTH)]
?
?????#?使用排序算法的名稱和剛創(chuàng)建的數(shù)組調(diào)用該函數(shù)
?????run_sorting_algorithm(algorithm="bubble_sort",?array=array)

現(xiàn)在運(yùn)行腳本來(lái)獲取bubble_sort的執(zhí)行時(shí)間：

$?python?sorting.py
Algorithm:?bubble_sort.?Minimum?execution?time:?73.21720498399998

分析冒泡排序的優(yōu)缺點(diǎn)

冒泡排序算法的主要優(yōu)點(diǎn)是它的簡(jiǎn)單性，理解起來(lái)非常簡(jiǎn)單。但也看到了冒泡排序的缺點(diǎn)是速度慢，運(yùn)行時(shí)間復(fù)雜度為O（n?²）。因此，一般對(duì)大型數(shù)組進(jìn)行排序的時(shí)候，不會(huì)考慮使用冒泡排序。

Python中的插入排序算法

像冒泡排序一樣，插入排序算法也易于實(shí)現(xiàn)和理解。但是與冒泡排序不同，它通過(guò)將每個(gè)元素與列表的其余元素進(jìn)行比較并將其插入正確的位置，來(lái)一次構(gòu)建一個(gè)排序的列表元素。此“插入”過(guò)程為算法命名。

一個(gè)例子，就是對(duì)一副紙牌進(jìn)行排序。將一張卡片與其余卡片進(jìn)行逐個(gè)比較，直到找到正確的位置為止，然后重復(fù)進(jìn)行直到您手中的所有卡都被排序。

在Python中實(shí)現(xiàn)插入排序

插入排序算法的工作原理與紙牌排序完全相同，Python中的實(shí)現(xiàn)：

??def?insertion_sort(array):
????#?從數(shù)據(jù)第二個(gè)元素開(kāi)始循環(huán)，直到最后一個(gè)元素
????for?i?in?range(1,?len(array)):
????????#?這個(gè)是我們想要放在正確位置的元素
????????key_item?=?array[i]

????????#?初始化變量，用于尋找元素正確位置
????????j?=?i?-?1

????????#?遍歷元素左邊的列表元素，一旦key_item比被比較元素小，那么找到正確位置插入。
????????while?j?>=?0?and?array[j]?>?key_item:
????????????#?把被檢測(cè)元素向左平移一個(gè)位置，并將j指向下一個(gè)元素（從右向左）
????????????array[j?+?1]?=?array[j]
????????????j?-=?1

????????#?當(dāng)完成元素位置的變換，把key_item放在正確的位置上
????????array[j?+?1]?=?key_item

????return?array

下圖顯示了對(duì)數(shù)組進(jìn)行排序時(shí)算法的不同迭代[8, 2, 6, 4, 5]：

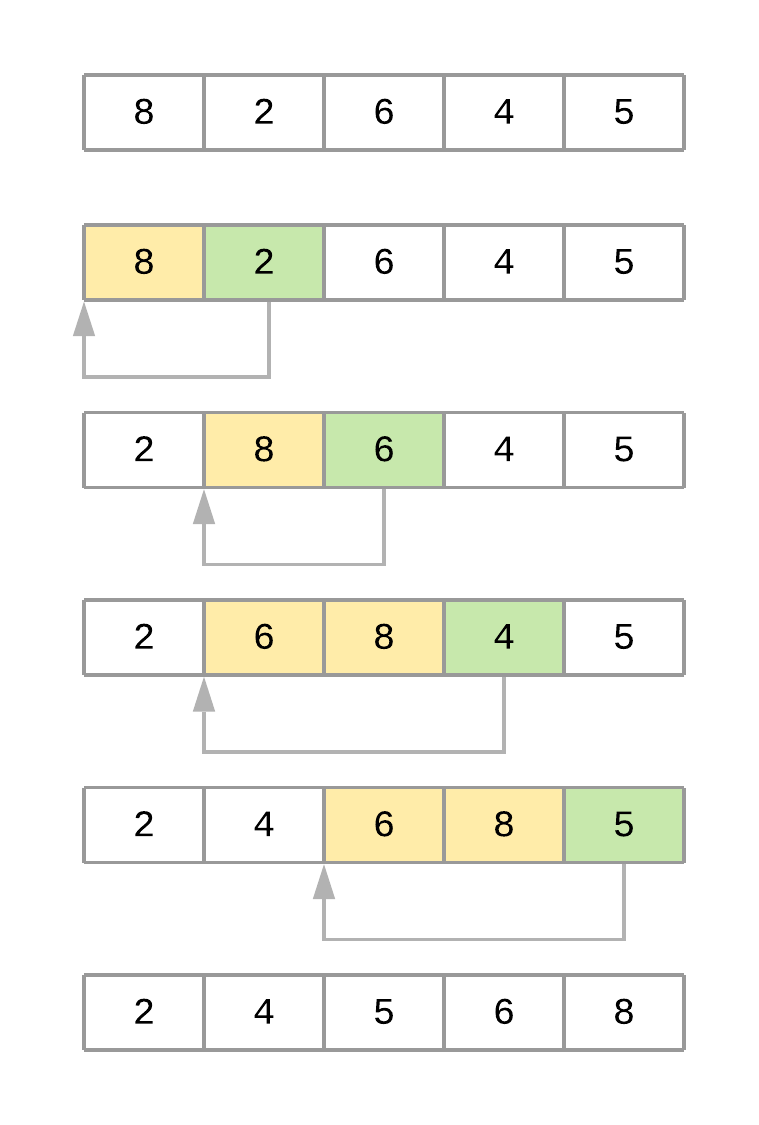
插入排序過(guò)程

測(cè)量插入排序的大O時(shí)間復(fù)雜度

與冒泡排序?qū)崿F(xiàn)類似，插入排序算法具有兩個(gè)嵌套循環(huán)，遍歷整個(gè)列表。內(nèi)部循環(huán)非常有效，因?yàn)樗鼤?huì)遍歷列表，直到找到元素的正確位置為止。

最壞的情況發(fā)生在所提供的數(shù)組以相反順序排序時(shí)。在這種情況下，內(nèi)部循環(huán)必須執(zhí)行每個(gè)比較，以將每個(gè)元素放置在正確的位置。這仍然給您帶來(lái)O（n²）運(yùn)行時(shí)復(fù)雜性。

最好的情況是對(duì)提供的數(shù)組進(jìn)行了排序。這里，內(nèi)部循環(huán)永遠(yuǎn)不會(huì)執(zhí)行，導(dǎo)致運(yùn)行時(shí)復(fù)雜度為O（n），就像冒泡排序的最佳情況一樣。

盡管冒泡排序和插入排序具有相同的大O時(shí)間復(fù)雜度，但實(shí)際上，插入排序比冒泡排序有效得多。如果查看兩種算法的實(shí)現(xiàn)，就會(huì)看到插入排序是如何減少了對(duì)列表進(jìn)行排序的比較次數(shù)的。

插入排序時(shí)間測(cè)算

為了證明插入排序比冒泡排序更有效，可以對(duì)插入排序算法進(jìn)行計(jì)時(shí)，并將其與冒泡排序的結(jié)果進(jìn)行比較。調(diào)用我們寫(xiě)好的測(cè)試函數(shù)。

??if?__name__?==?"__main__":
?????#?生成包含“?ARRAY_LENGTH”個(gè)元素的數(shù)組，元素是介于0到999之間的隨機(jī)整數(shù)值
?????array?=?[randint(0,?1000)?for?i?in?range(ARRAY_LENGTH)]
?
?????#?使用排序算法的名稱和剛創(chuàng)建的數(shù)組調(diào)用該函數(shù)
????run_sorting_algorithm(algorithm="insertion_sort",?array=array)

執(zhí)行腳本：

??$?python?sorting.py
Algorithm:?insertion_sort.?Minimum?execution?time:?56.71029764299999

可以看到，插入排序比冒泡排序?qū)崿F(xiàn)少了17秒，即使它們都是O（n 2）算法，插入排序也更加有效。

分析插入排序的優(yōu)點(diǎn)和缺點(diǎn)

就像冒泡排序一樣，插入排序算法的實(shí)現(xiàn)也很簡(jiǎn)單。盡管插入排序是O（n 2）算法，但在實(shí)踐中它也比其他二次實(shí)現(xiàn)（例如冒泡排序）更有效。

有更強(qiáng)大的算法，包括合并排序和快速排序，但是這些實(shí)現(xiàn)是遞歸的，在處理小型列表時(shí)通常無(wú)法擊敗插入排序。如果列表足夠小，可以提供更快的整體實(shí)現(xiàn)，則某些快速排序?qū)崿F(xiàn)甚至在內(nèi)部使用插入排序。Timsort還在內(nèi)部使用插入排序?qū)斎霐?shù)組的一小部分進(jìn)行排序。

也就是說(shuō)，插入排序不適用于大型陣列，這為可以更有效地?cái)U(kuò)展規(guī)模的算法打開(kāi)了大門(mén)。

Python中的合并排序算法

合并排序是一種非常有效的排序算法。它基于分治法，這是一種用于解決復(fù)雜問(wèn)題的強(qiáng)大算法技術(shù)。

要正確理解分而治之，應(yīng)該首先了解遞歸的概念。遞歸涉及將問(wèn)題分解成較小的子問(wèn)題，直到它們足夠小以至于無(wú)法解決。在編程中，遞歸通常由調(diào)用自身的函數(shù)表示。

分而治之算法通常遵循相同的結(jié)構(gòu)：

原始輸入分為幾個(gè)部分，每個(gè)部分代表一個(gè)子問(wèn)題，該子問(wèn)題與原始輸入相似，但更為簡(jiǎn)單。每個(gè)子問(wèn)題都遞歸解決。所有子問(wèn)題的解決方案都組合成一個(gè)整體解決方案。在合并排序的情況下，分而治之方法將輸入值的集合劃分為兩個(gè)大小相等的部分，對(duì)每個(gè)一半進(jìn)行遞歸排序，最后將這兩個(gè)排序的部分合并為一個(gè)排序列表。

在Python中實(shí)現(xiàn)合并排序

合并排序算法的實(shí)現(xiàn)需要兩個(gè)不同的部分：

遞歸地將輸入分成兩半的函數(shù) 合并兩個(gè)半部的函數(shù)，產(chǎn)生一個(gè)排序數(shù)組 這是合并兩個(gè)不同數(shù)組的代碼：

def?merge(left,?right):
??#?如果第一個(gè)數(shù)組為空，那么不需要合并，
??#?可以直接將第二個(gè)數(shù)組返回作為結(jié)果
??if?len(left)?==?0:
??????return?right

? #?如果第二個(gè)數(shù)組為空，那么不需要合并，
??#?可以直接將第一個(gè)數(shù)組返回作為結(jié)果
??if?len(right)?==?0:
??????return?left

??result?=?[]
??index_left?=?index_right?=?0

??#?查看兩個(gè)數(shù)組直到所有元素都裝進(jìn)結(jié)果數(shù)組中
??while?len(result)???????#?這些需要排序的元素要依次被裝入結(jié)果列表，因此需要決定將從
??????#?第一個(gè)還是第二個(gè)數(shù)組中取下一個(gè)元素
??????if?left[index_left]?<=?right[index_right]:
??????????result.append(left[index_left])
??????????index_left?+=?1
??????else:
??????????result.append(right[index_right])
??????????index_right?+=?1

??????#?如果哪個(gè)數(shù)組達(dá)到了最后一個(gè)元素，那么可以將另外一個(gè)數(shù)組的剩余元素
??????#?裝進(jìn)結(jié)果列表中，然后終止循環(huán)
??????if?index_right?==?len(right):
??????????result?+=?left[index_left:]
??????????break

??????if?index_left?==?len(left):
??????????result?+=?right[index_right:]
??????????break

??return?result

現(xiàn)在還缺少的部分是將輸入數(shù)組遞歸拆分為兩個(gè)并用于merge()產(chǎn)生最終結(jié)果的函數(shù)：

def?merge_sort(array):
??#?如果輸入數(shù)組包含元素不超過(guò)兩個(gè)，那么返回它作為函數(shù)結(jié)果
??if?len(array)?2:
??????return?array

??midpoint?=?len(array)?//?2

??#?對(duì)數(shù)組遞歸地劃分為兩部分，排序每部分然后合并裝進(jìn)最終結(jié)果列表
??return?merge(
??????left=merge_sort(array[:midpoint]),
??????right=merge_sort(array[midpoint:]))

看一下合并排序?qū)?duì)數(shù)組進(jìn)行排序的步驟[8, 2, 6, 4, 5]：

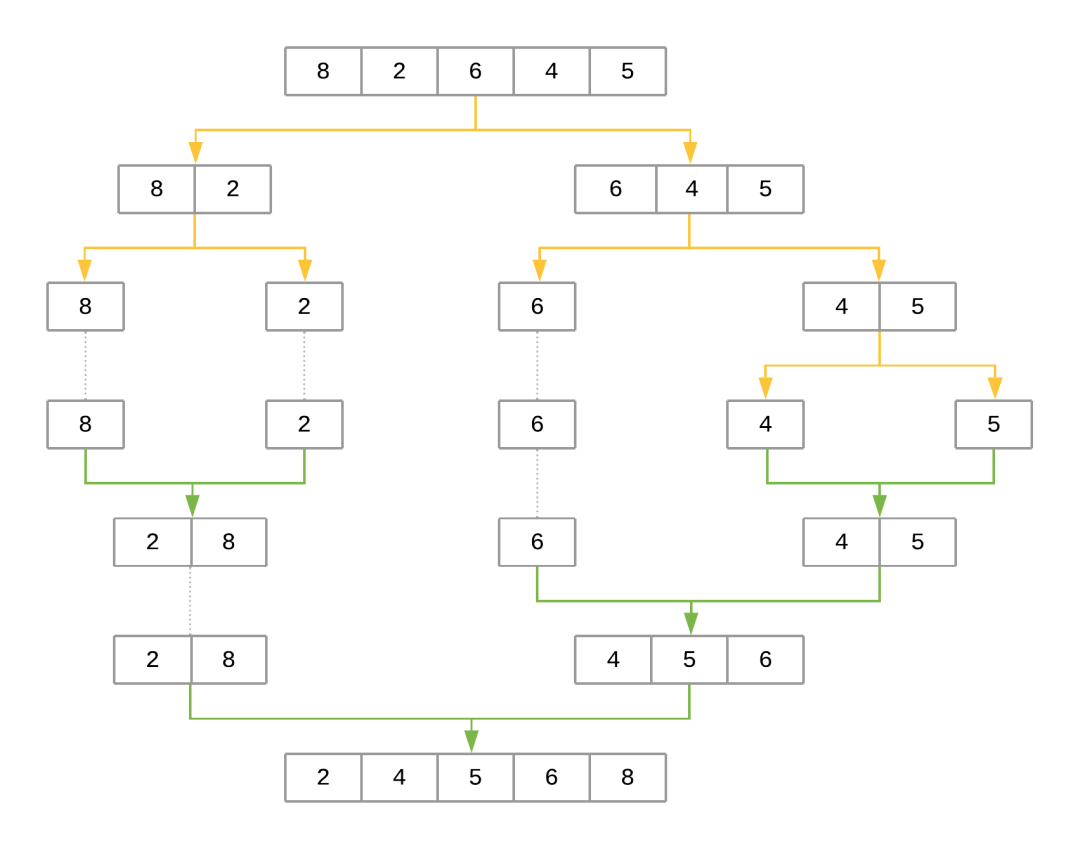
合并排序過(guò)程

該圖使用黃色箭頭表示在每個(gè)遞歸級(jí)別將數(shù)組減半。綠色箭頭表示將每個(gè)子陣列合并在一起。

衡量合并排序的大O復(fù)雜度

要分析合并排序的復(fù)雜性，可以分別查看其兩個(gè)步驟：

merge()具有線性運(yùn)行時(shí)間。它接收兩個(gè)數(shù)組，它們的組合長(zhǎng)度最多為n（原始輸入數(shù)組的長(zhǎng)度），并且通過(guò)最多查看每個(gè)元素一次來(lái)組合兩個(gè)數(shù)組。這導(dǎo)致運(yùn)行時(shí)復(fù)雜度為O（n）。

第二步以遞歸方式拆分輸入數(shù)組，并調(diào)用merge()每一部分。由于將數(shù)組減半直到剩下單個(gè)元素，因此此功能執(zhí)行的減半運(yùn)算總數(shù)為log 2 n。由于merge()每個(gè)部分都被調(diào)用，因此總運(yùn)行時(shí)間為O（n log 2 n）。

對(duì)合并排序進(jìn)行測(cè)算時(shí)間

同樣通過(guò)之前時(shí)間測(cè)試函數(shù)：

if?__name__?==?"__main__":
?????#?生成包含“?ARRAY_LENGTH”個(gè)元素的數(shù)組，元素是介于0到999之間的隨機(jī)整數(shù)值
?????array?=?[randint(0,?1000)?for?i?in?range(ARRAY_LENGTH)]
?
?????#?使用排序算法的名稱和剛創(chuàng)建的數(shù)組調(diào)用該函數(shù)
????run_sorting_algorithm(algorithm="merge_sort",?array=array)

執(zhí)行時(shí)間：

$?python?sorting.py
Algorithm:?merge_sort.?Minimum?execution?time:?0.6195857160000173

與冒泡排序和插入排序相比，合并排序?qū)崿F(xiàn)非常快，可以在一秒鐘內(nèi)對(duì)一萬(wàn)個(gè)數(shù)組進(jìn)行排序了！

分析合并排序的優(yōu)點(diǎn)和缺點(diǎn)

由于其運(yùn)行時(shí)復(fù)雜度為O（n log 2 n），因此合并排序是一種非常有效的算法，可以隨著輸入數(shù)組大小的增長(zhǎng)而很好地?cái)U(kuò)展。并行化也很簡(jiǎn)單，因?yàn)樗鼘⑤斎霐?shù)組分成多個(gè)塊，必要時(shí)可以并行分配和處理這些塊。

缺點(diǎn)是對(duì)于較小的列表，遞歸的時(shí)間成本就較高了，冒泡排序和插入排序之類的算法更快。例如，運(yùn)行包含十個(gè)元素的列表的實(shí)驗(yàn)的時(shí)間：

Algorithm:?bubble_sort.?Minimum?execution?time:?0.000018774999999998654
Algorithm:?insertion_sort.?Minimum?execution?time:?0.000029786000000000395
Algorithm:?merge_sort.?Minimum?execution?time:?0.00016983000000000276

合并排序的另一個(gè)缺點(diǎn)是，它在遞歸調(diào)用自身時(shí)會(huì)創(chuàng)建數(shù)組。它還在內(nèi)部創(chuàng)建一個(gè)新列表，這使得合并排序比氣泡排序和插入排序使用更多的內(nèi)存。

Python中的快速排序算法

就像合并排序一樣，快速排序算法采用分而治之的原理將輸入數(shù)組分為兩個(gè)列表，第一個(gè)包含小項(xiàng)目，第二個(gè)包含大項(xiàng)目。然后，該算法將對(duì)兩個(gè)列表進(jìn)行遞歸排序，直到對(duì)結(jié)果列表進(jìn)行完全排序?yàn)橹埂?/p>

劃分輸入列表稱為對(duì)列表進(jìn)行分區(qū)。快排首先選擇一個(gè)pivot元素，然后將列表劃分為pivot，然后將每個(gè)較小的元素放入low數(shù)組，將每個(gè)較大的元素放入high數(shù)組。

將low列表中的每個(gè)元素放在列表的左側(cè)，列表中的pivot每個(gè)元素high放在右側(cè)，將其pivot精確定位在最終排序列表中的確切位置。這意味著該函數(shù)現(xiàn)在可以遞歸地將相同的過(guò)程應(yīng)用于low，然后high對(duì)整個(gè)列表進(jìn)行排序。

在Python中實(shí)現(xiàn)快排

這是快排的一個(gè)相當(dāng)緊湊的實(shí)現(xiàn)：

from?random?import?randint

def?quicksort(array):
??  #?如果第一個(gè)數(shù)組為空，那么不需要合并，
??  #?可以直接將第二個(gè)數(shù)組返回作為結(jié)果
????if?len(array)?2:
????????return?array

????low,?same,?high?=?[],?[],?[]

????#?隨機(jī)選擇 pivot 元素
????pivot?=?array[randint(0,?len(array)?-?1)]

????for?item?in?array:
????????#?元素小于pivot元素的裝進(jìn)low列表中，大于piviot元素值的裝進(jìn)high列表中
????????#?如果和pivot相等，則裝進(jìn)same列表中
????????if?item?????????????low.append(item)
????????elif?item?==?pivot:
????????????same.append(item)
????????elif?item?>?pivot:
????????????high.append(item)

????#?最后的結(jié)果列表包含排序的low列表、same列表、hight列表
????return?quicksort(low)?+?same?+?quicksort(high)

以下是快排對(duì)數(shù)組進(jìn)行排序的步驟的說(shuō)明[8, 2, 6, 4, 5]：

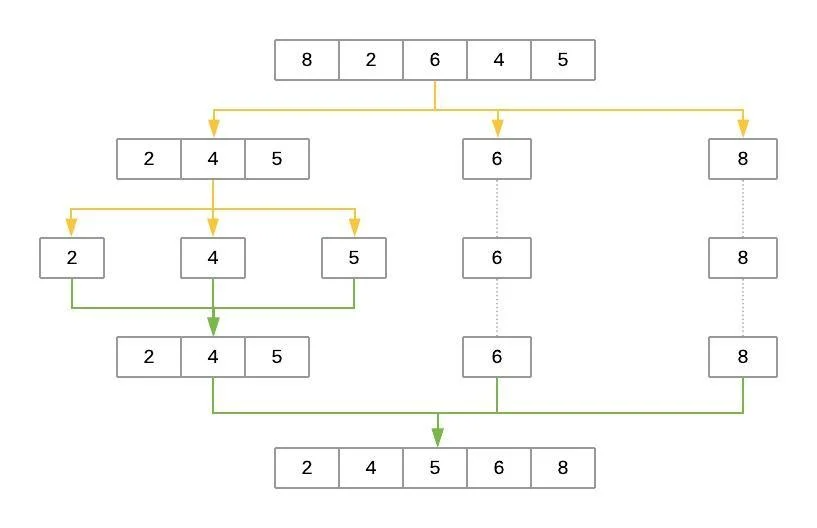
快排排序過(guò)程

快速排序流程 黃線表示陣列的劃分成三個(gè)列表：low，same，high。綠線表示排序并將這些列表放在一起。

選擇pivot元素

為什么上面的實(shí)現(xiàn)會(huì)pivot隨機(jī)選擇元素？選擇輸入列表的第一個(gè)或最后一個(gè)元素會(huì)不會(huì)一樣？

由于快速排序算法的工作原理，遞歸級(jí)別的數(shù)量取決于pivot每個(gè)分區(qū)的結(jié)尾位置。在最佳情況下，算法始終選擇中值元素作為pivot。這將使每個(gè)生成的子問(wèn)題恰好是前一個(gè)問(wèn)題的一半，從而導(dǎo)致最多l(xiāng)og 2 n級(jí)。

另一方面，如果算法始終選擇數(shù)組的最小或最大元素作為pivot，則生成的分區(qū)將盡可能不相等，從而導(dǎo)致n-1個(gè)遞歸級(jí)別。對(duì)于快速排序，那將是最壞的情況。

如你所見(jiàn)，快排的效率通常取決于pivot選擇。如果輸入數(shù)組未排序，則將第一個(gè)或最后一個(gè)元素用作，pivot將與隨機(jī)元素相同。但是，如果輸入數(shù)組已排序或幾乎已排序，則使用第一個(gè)或最后一個(gè)元素作為pivot可能導(dǎo)致最壞的情況。pivot隨機(jī)選擇使其更有可能使快排選擇一個(gè)接近中位數(shù)的值并更快地完成。

另一個(gè)選擇是找到數(shù)組的中值，并強(qiáng)制算法將其用作pivot。這可以在O（n）時(shí)間內(nèi)完成。盡管該過(guò)程稍微復(fù)雜一些，但將中值用作pivot快速排序可以確保您擁有最折中的大O方案。

衡量快排的大O復(fù)雜度

使用快排，將輸入列表按線性時(shí)間O（n）進(jìn)行分區(qū)，并且此過(guò)程將平均遞歸地重復(fù)log 2 n次。這導(dǎo)致最終復(fù)雜度為O（n log 2 n）。

當(dāng)所選擇的pivot是接近陣列的中位數(shù)，最好的情況下會(huì)發(fā)生O（n），當(dāng)pivot是陣列的最小或最大的值，最差的時(shí)間復(fù)雜度為O（n 2）。

從理論上講，如果算法首先專注于找到中值，然后將其用作pivot元素，那么最壞情況下的復(fù)雜度將降至O（n log 2 n）。數(shù)組的中位數(shù)可以在線性時(shí)間內(nèi)找到，并將其用作pivot保證代碼的快速排序部分將在O（n log 2 n）中執(zhí)行。

通過(guò)使用中值作為pivot，最終運(yùn)行時(shí)間為O（n）+ O（n log 2 n）。你可以將其簡(jiǎn)化為O（n log 2 n），因?yàn)閷?duì)數(shù)部分的增長(zhǎng)快于線性部分。

隨機(jī)選擇pivot使最壞情況發(fā)生的可能性很小。這使得隨機(jī)pivot選擇對(duì)于該算法的大多數(shù)實(shí)現(xiàn)都足夠好。

對(duì)快排測(cè)量運(yùn)行時(shí)間

調(diào)用測(cè)試函數(shù)：

if?__name__?==?"__main__":
?????#?生成包含“?ARRAY_LENGTH”個(gè)元素的數(shù)組，元素是介于0到999之間的隨機(jī)整數(shù)值
?????array?=?[randint(0,?1000)?for?i?in?range(ARRAY_LENGTH)]
?
?????#?使用排序算法的名稱和剛創(chuàng)建的數(shù)組調(diào)用該函數(shù)
????run_sorting_algorithm(algorithm="quicksort",?array=array)

執(zhí)行腳本：

$?python?sorting.py
Algorithm:?quicksort.?Minimum?execution?time:?0.11675417600002902

快速排序不僅可以在不到一秒鐘的時(shí)間內(nèi)完成，而且比合并排序（0.11幾秒鐘對(duì)0.61幾秒鐘）要快得多。如果增加ARRAY_LENGTH從10,000到數(shù)量1,000,000并再次運(yùn)行腳本，合并排序最終會(huì)在97幾秒鐘內(nèi)完成，而快排則僅在10幾秒鐘內(nèi)對(duì)列表進(jìn)行排序。

分析快排的優(yōu)勢(shì)和劣勢(shì)

顧名思義，快排非常快。盡管從理論上講，它的最壞情況是O（n 2），但在實(shí)踐中，快速排序的良好實(shí)現(xiàn)勝過(guò)大多數(shù)其他排序?qū)崿F(xiàn)。而且，就像合并排序一樣，快排也很容易并行化。

快排的主要缺點(diǎn)之一是缺乏保證達(dá)到平均運(yùn)行時(shí)復(fù)雜度的保證。盡管最壞的情況很少見(jiàn)，但是某些應(yīng)用程序不能承受性能不佳的風(fēng)險(xiǎn)，因此無(wú)論輸入如何，它們都選擇不超過(guò)O（n log 2 n）的算法。

就像合并排序一樣，快排也會(huì)在內(nèi)存空間與速度之間進(jìn)行權(quán)衡。這可能成為對(duì)較大列表進(jìn)行排序的限制。

通過(guò)快速實(shí)驗(yàn)對(duì)十個(gè)元素的列表進(jìn)行排序，可以得出以下結(jié)果：

Algorithm:?bubble_sort.?Minimum?execution?time:?0.0000909000000000014
Algorithm:?insertion_sort.?Minimum?execution?time:?0.00006681900000000268
Algorithm:?quicksort.?Minimum?execution?time:?0.0001319930000000004

結(jié)果表明，當(dāng)列表足夠小時(shí)，快速排序也要付出遞歸的代價(jià)，完成時(shí)間比插入排序和冒泡排序都要長(zhǎng)。

Python中的Timsort算法

最后這個(gè)算法就有意思了！

所述Timsort算法被認(rèn)為是一種混合的排序算法，因?yàn)樗捎貌迦肱判蚝秃喜⑴判虻淖罴训膬蓚€(gè)世界級(jí)組合。Timsort與Python社區(qū)也很有緣，它是由Tim Peters于2002年創(chuàng)建的，被用作Python語(yǔ)言的標(biāo)準(zhǔn)排序算法。我們使用的內(nèi)置sorted函數(shù)就是這個(gè)算法。

Timsort的主要特征是它利用了大多數(shù)現(xiàn)實(shí)數(shù)據(jù)集中存在的已排序元素。這些稱為natural runs。然后，該算法會(huì)遍歷列表，將元素收集到運(yùn)行中，然后將它們合并到一個(gè)排序的列表中。

在Python中實(shí)現(xiàn)Timsort

本篇?jiǎng)?chuàng)建一個(gè)準(zhǔn)系統(tǒng)的Python實(shí)現(xiàn)，該實(shí)現(xiàn)說(shuō)明Timsort算法的所有部分。如果有興趣，也可以查看Timsort的原始C實(shí)現(xiàn)。

實(shí)施Timsort的第一步是修改insertion_sort()的實(shí)現(xiàn)：

def?insertion_sort(array,?left=0,?right=None):
????if?right?is?None:
????????right?=?len(array)?-?1

????#?從指示的left元素循環(huán)，直到right被指示
????for?i?in?range(left?+?1,?right?+?1):
        #?這個(gè)是我們想要放在正確位置的元素
????????key_item?=?array[i]

?       #?初始化變量，用于尋找元素正確位置
????????j?=?i?-?1
        #?遍歷元素左邊的列表元素，一旦key_item比被比較元素小，那么找到正確位置插入
????????while?j?>=?left?and?array[j]?>?key_item:
            #?把被檢測(cè)元素向左平移一個(gè)位置，并將j指向下一個(gè)元素（從右向左）
????????????array[j?+?1]?=?array[j]
????????????j?-=?1

        #?當(dāng)完成元素位置的變換，把key_item放在正確的位置上
????????array[j?+?1]?=?key_item

????return?array

此修改后的實(shí)現(xiàn)添加了兩個(gè)參數(shù)left和right，它們指示應(yīng)該對(duì)數(shù)組的哪一部分進(jìn)行排序。這使Timsort算法可以對(duì)數(shù)組的一部分進(jìn)行排序。修改功能而不是創(chuàng)建新功能意味著可以將其同時(shí)用于插入排序和Timsort。

現(xiàn)在看一下Timsort的實(shí)現(xiàn)：

def?timsort(array):
????min_run?=?32
????n?=?len(array)

????#?開(kāi)始切分、排序輸入數(shù)組的小部分，切分在`min_run`定義
????for?i?in?range(0,?n,?min_run):
????????insertion_sort(array,?i,?min((i?+?min_run?-?1),?n?-?1))

????#?現(xiàn)在可以合并排序的切分塊了
????#?從`min_run`開(kāi)始,?每次循環(huán)都加倍直到超過(guò)數(shù)組的長(zhǎng)度
????size?=?min_run
????while?size?????????#?Determine?the?arrays?that?will
????????#?be?merged?together
????????for?start?in?range(0,?n,?size?*?2):
????????????#?計(jì)算中點(diǎn)（第一個(gè)數(shù)組結(jié)束第二個(gè)數(shù)組開(kāi)始的地方）和終點(diǎn)(第二個(gè)數(shù)組結(jié)束的地方)
????????????midpoint?=?start?+?size?-?1
????????????end?=?min((start?+?size?*?2?-?1),?(n-1))

????????????#?合并兩個(gè)子數(shù)組
????????????#?left數(shù)組應(yīng)該從起點(diǎn)到中點(diǎn)+1,?right數(shù)組應(yīng)該從中點(diǎn)+1到終點(diǎn)+1
????????????merged_array?=?merge(
????????????????left=array[start:midpoint?+?1],
????????????????right=array[midpoint?+?1:end?+?1])

????????????#?最后，把合并的數(shù)組放回?cái)?shù)組
????????????array[start:start?+?len(merged_array)]?=?merged_array

????????#?每次迭代都應(yīng)該讓數(shù)據(jù)size加倍
????????size?*=?2

????return?array

盡管實(shí)現(xiàn)比以前的算法要復(fù)雜一些，但是我們可以通過(guò)以下方式快速總結(jié)一下：

之前已經(jīng)了解到，插入排序在小列表上速度很快，而Timsort則利用了這一優(yōu)勢(shì)。Timsort使用新引入的left和right參數(shù)在insertion_sort()對(duì)列表進(jìn)行適當(dāng)排序，而不必像merge sort和快排那樣創(chuàng)建新數(shù)組。

定義min_run = 32作為值有兩個(gè)原因：

1. 使用插入排序?qū)π?shù)組進(jìn)行排序非常快，并且min_run利用此特性的價(jià)值很小。使用min_run太大的值進(jìn)行初始化將無(wú)法達(dá)到使用插入排序的目的，并使算法變慢。

2. 合并兩個(gè)平衡列表比合并不成比例的列表要有效得多。min_run在合并算法創(chuàng)建的所有不同運(yùn)行時(shí)，選擇一個(gè)為2的冪的值可確保更好的性能。

結(jié)合以上兩個(gè)條件，可以提供幾種min_run選擇。本教程中的實(shí)現(xiàn)min_run = 32是其中一種可能性。

衡量Timsort的大O時(shí)間復(fù)雜性

平均而言，Timsort的復(fù)雜度為O（n log 2 n），就像合并排序和快速排序一樣。對(duì)數(shù)部分來(lái)自執(zhí)行每個(gè)線性合并操作的運(yùn)行大小加倍。

但是，Timsort在已排序或接近排序的列表上表現(xiàn)特別出色，從而導(dǎo)致了O（n）的最佳情況。在這種情況下，Timsort明顯勝過(guò)合并排序，并與快速排序的最佳情況相匹配。但是，對(duì)于Timsort來(lái)說(shuō)，最糟糕的情況也是O（n log 2 n）。

對(duì)Timsort測(cè)量運(yùn)行時(shí)間

調(diào)用時(shí)間運(yùn)行測(cè)試函數(shù)：

if?__name__?==?"__main__":
?????#?生成包含“?ARRAY_LENGTH”個(gè)元素的數(shù)組，元素是介于0到999之間的隨機(jī)整數(shù)值
?????array?=?[randint(0,?1000)?for?i?in?range(ARRAY_LENGTH)]
?
?????#?使用排序算法的名稱和剛創(chuàng)建的數(shù)組調(diào)用該函數(shù)
????run_sorting_algorithm(algorithm="timsort",?array=array)

執(zhí)行時(shí)間：

$?python?sorting.py
Algorithm:?timsort.?Minimum?execution?time:?0.5121690789999998

0.51秒，Timsort比合并排序整整快0.1秒，即17％。它也比插入排序快11,000％！

現(xiàn)在，嘗試使用這四種算法對(duì)已經(jīng)排序的列表進(jìn)行排序，然后看看會(huì)發(fā)生什么。

if?__name__?==?"__main__":
????#?生成包含“?ARRAY_LENGTH”個(gè)元素的數(shù)組
????array?=?[i?for?i?in?range(ARRAY_LENGTH)]

????#?調(diào)用每個(gè)函數(shù)
????run_sorting_algorithm(algorithm="insertion_sort",?array=array)
????run_sorting_algorithm(algorithm="merge_sort",?array=array)
????run_sorting_algorithm(algorithm="quicksort",?array=array)
????run_sorting_algorithm(algorithm="timsort",?array=array)

現(xiàn)在執(zhí)行腳本，那么所有算法都將運(yùn)行并輸出相應(yīng)的執(zhí)行時(shí)間：

Algorithm:?insertion_sort.?Minimum?execution?time:?53.5485634999991
Algorithm:?merge_sort.?Minimum?execution?time:?0.372304601
Algorithm:?quicksort.?Minimum?execution?time:?0.24626494199999982
Algorithm:?timsort.?Minimum?execution?time:?0.23350277099999994

這次，Timsort的速度比合并排序快了37％，比快排快了5％，從而增強(qiáng)了利用已排序運(yùn)行的能力。

請(qǐng)注意，Timsort如何從兩種算法中受益，這兩種算法單獨(dú)使用時(shí)速度要慢得多。Timsort的神奇之處在于將這些算法結(jié)合起來(lái)并發(fā)揮其優(yōu)勢(shì)，以獲得令人印象深刻的結(jié)果。

分析Timsort的優(yōu)勢(shì)和劣勢(shì)

Timsort的主要缺點(diǎn)是它的復(fù)雜性。盡管實(shí)現(xiàn)了原始算法的非常簡(jiǎn)化的版本，但由于它同時(shí)依賴于insertion_sort()和merge()，因此仍需要更多代碼。

Timsort的優(yōu)點(diǎn)之一是其能夠以O(shè)（n log 2 n）的方式執(zhí)行預(yù)測(cè)，而與輸入數(shù)組的結(jié)構(gòu)無(wú)關(guān)。與快排相比，快排可以降級(jí)為O（n 2）。對(duì)于小數(shù)組，Timsort也非常快，因?yàn)樵撍惴ㄗ兂闪藛蝹€(gè)插入排序。

對(duì)于現(xiàn)實(shí)世界中的使用（通常對(duì)已經(jīng)具有某些預(yù)先存在的順序的數(shù)組進(jìn)行排序），Timsort是一個(gè)不錯(cuò)的選擇。它的適應(yīng)性使其成為排序任何長(zhǎng)度的數(shù)組的絕佳選擇。

結(jié)論

排序是任何Pythonista工具包中必不可少的工具。了解Python中不同的排序算法以及如何最大程度地發(fā)揮它們的潛力，你就可以實(shí)現(xiàn)更快，更高效的應(yīng)用程序和程序！

參考：?

1. https://realpython.com/sorting-algorithms-python/

2. https://blog.csdn.net/weixin_38483589/article/details/84147376

3. https://mp.weixin.qq.com/s/OHoe6TTX--Ys5G-5yR6juA