從歸并排序引發(fā)的思考

點(diǎn)擊上方“服務(wù)端思維”，選擇“設(shè)為星標(biāo)”

回復(fù)”669“獲取獨(dú)家整理的精選資料集

回復(fù)”加群“加入全國(guó)服務(wù)端高端社群「后端圈」

有非常多的同學(xué)，包括小孩子都曾經(jīng)或者正在覺(jué)得用代碼實(shí)現(xiàn)某個(gè)算法就像是在做腦經(jīng)急轉(zhuǎn)彎——看過(guò)答案之后你會(huì)覺(jué)得非常簡(jiǎn)單，但自己就是寫(xiě)不出來(lái)>_<

問(wèn)題到底是出在哪里了呢？本篇文章從一個(gè)非常簡(jiǎn)單，但卻蘊(yùn)含著十分重要的算法思想的歸并排序入手，以一個(gè)完全小白的視角來(lái)考慮一下我們實(shí)現(xiàn)這個(gè)算法的時(shí)候到底會(huì)遇到哪些坑，以及如何解決它們。

什么是歸并排序？

為防止一部分小伙伴可能并不知道歸并排序是個(gè)啥，我們先來(lái)介紹一下。

歸并排序是一個(gè)非常經(jīng)典的排序算法，這個(gè)算法特簡(jiǎn)單，一句話就可以描述完：將一個(gè)待排序數(shù)組分成兩個(gè)子數(shù)組，先分別對(duì)兩個(gè)子數(shù)組進(jìn)行排序，然后再將兩個(gè)排好序的子數(shù)組合并成一個(gè)大的排序數(shù)組。

簡(jiǎn)單的描述里隱藏著3個(gè)細(xì)節(jié)：

?細(xì)節(jié)1：問(wèn)題的分解（Divide）：如何將一個(gè)待排序數(shù)組拆分成兩個(gè)子數(shù)組？

?細(xì)節(jié)2：子問(wèn)題的解決（Conquer）：如何對(duì)兩個(gè)子數(shù)組進(jìn)行排序？

?細(xì)節(jié)3：子問(wèn)題的合并（Combine）：如何將兩個(gè)有序的子數(shù)組合并為一個(gè)大的有序數(shù)組？

下邊分析一下上述3個(gè)細(xì)節(jié)。

細(xì)節(jié)1

將一個(gè)數(shù)組拆分成兩個(gè)子數(shù)組非常簡(jiǎn)單，只需要算出中間元素的下標(biāo)，那我們可以規(guī)定：

?從數(shù)組開(kāi)頭的元素到中間元素屬于一個(gè)子數(shù)組

?從中間元素的后一個(gè)元素開(kāi)始，到數(shù)組最后一個(gè)元素屬于另一個(gè)子數(shù)組

中間元素的下標(biāo) = (起始元素的下標(biāo) + 末尾元素的下標(biāo)) / 2

小貼士：這里請(qǐng)大家思考一下我們?yōu)槭裁床挥脭?shù)組中包含元素?cái)?shù)量除以2的方式來(lái)計(jì)算中間元素的下標(biāo)，如果以這種方式計(jì)算中間元素的下標(biāo)的話會(huì)發(fā)生什么事情（友情提示：可以按照數(shù)組中包含元素?cái)?shù)量是單數(shù)還是雙數(shù)來(lái)分開(kāi)討論）。

細(xì)節(jié)2

細(xì)節(jié)2其實(shí)很好解決，在對(duì)某個(gè)子數(shù)組進(jìn)行排序時(shí)，可以將這個(gè)子數(shù)組繼續(xù)分成兩個(gè)子子數(shù)組，先對(duì)這兩個(gè)子子數(shù)組進(jìn)行排序，然后再將這兩個(gè)排好序的子子數(shù)組進(jìn)行排序，就完成了對(duì)子數(shù)組的排序。

子子數(shù)組怎么排？繼續(xù)拆成兩個(gè)更小的數(shù)組排唄。這里成功的進(jìn)入了套娃模式，直到某個(gè)子子子...子數(shù)組里只包括1個(gè)元素就不用再拆了。

也就是說(shuō)我們可以將子問(wèn)題繼續(xù)拆分成多個(gè)子子問(wèn)題，然后進(jìn)入套娃模式，直到某個(gè)子問(wèn)題足夠簡(jiǎn)單為止（本例中就是直到子數(shù)組中僅包含1個(gè)元素為止）。

當(dāng)然，上邊的描述不是很直觀，我們具體舉個(gè)例子看一下。

我們有一個(gè)無(wú)序數(shù)組[2, 7, 1, 4, 6, 5, 0, 4]：

這個(gè)數(shù)組包含8個(gè)元素，我們把它分成兩個(gè)組：1組和2組，每個(gè)組都包含4個(gè)元素：

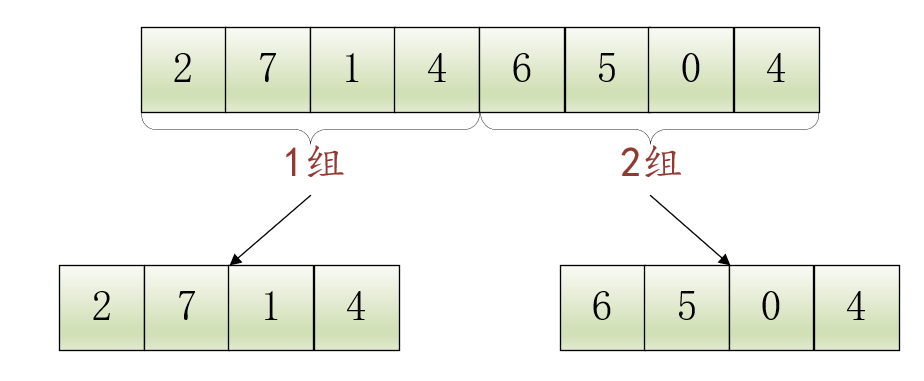
包含4個(gè)元素的數(shù)組還是太長(zhǎng)了，繼續(xù)將1組和2組分別拆分成2個(gè)組，現(xiàn)在就能得到4個(gè)組：1.1組、1.2組、2.1組、2.2組，每個(gè)組都包含2個(gè)元素：

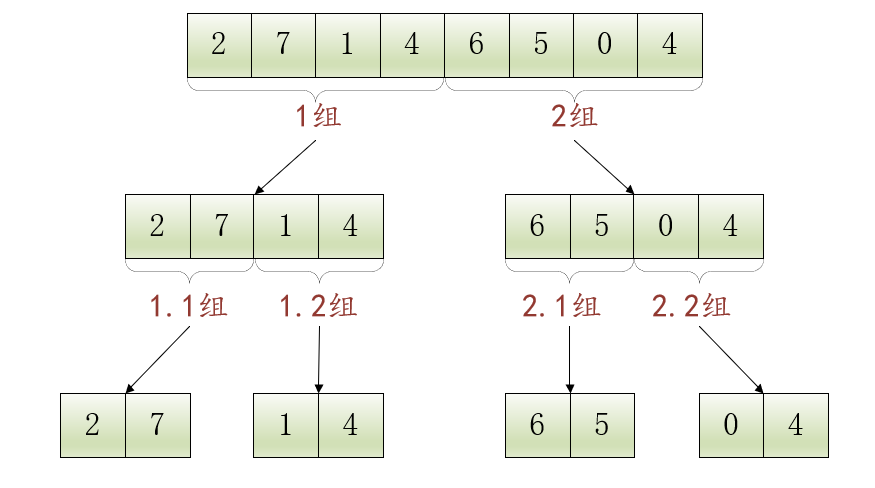
繼續(xù)拆分包含2個(gè)元素的數(shù)組，將得到8個(gè)組：1.1.1組、1.1.2組、1.2.1組、1.2.2組、2.1.1組、2.1.2組、2.2.1組、2.2.2組，每個(gè)組只包含1個(gè)元素：

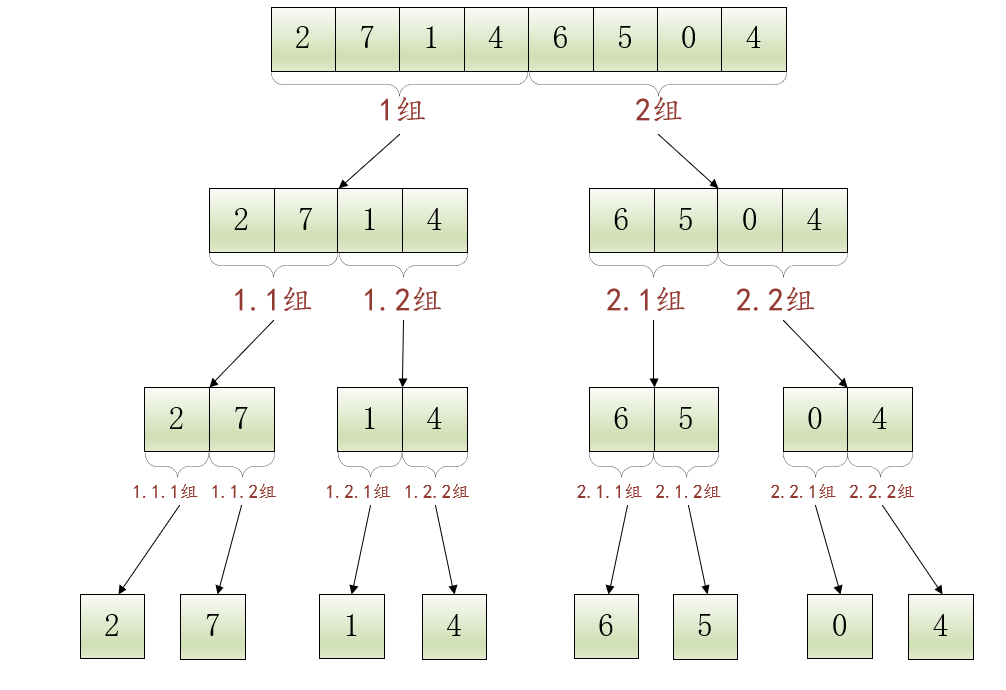
現(xiàn)在各個(gè)組僅包含1個(gè)元素，不能再拆分了，就可以對(duì)組中元素進(jìn)行排序了。很顯然，僅有1個(gè)元素的數(shù)組本身就是已經(jīng)排好序的，也就是說(shuō)：1.1.1組、1.1.2組、1.2.1組、1.2.2組、2.1.1組、2.1.2組、2.2.1組、2.2.2組這些僅包含1個(gè)元素的數(shù)組本身就是有序的，不用再額外進(jìn)行排序了。

細(xì)節(jié)3

細(xì)節(jié)3其實(shí)也很好解決，只要從頭開(kāi)始遍歷兩個(gè)子數(shù)組，每次都把兩個(gè)子數(shù)組中較小的元素加入到最后的結(jié)果中即可。

比方說(shuō)有兩個(gè)包含2個(gè)元素的已排序數(shù)組[2, 7]和[1, 4]，我們想把這兩個(gè)數(shù)組合并為一個(gè)大的有序數(shù)組，那么我們可以定義兩個(gè)變量i和j：

?i表示第1個(gè)子數(shù)組的下標(biāo)，初始指向第1個(gè)子數(shù)組的開(kāi)頭元素。

?j表示第2個(gè)子數(shù)組的下標(biāo)，初始指向第2個(gè)子數(shù)組的開(kāi)頭元素。

如下圖所示：

接著就可以依次向存放最終結(jié)果的數(shù)組中填入元素了：

?第1步：當(dāng)前i指向的元素是2，j指向的元素是1，比較i和j指向的元素哪個(gè)更小，由于2>1，所以將j指向的元素1填入結(jié)果數(shù)組中，并將j自增1，效果如下圖所示：

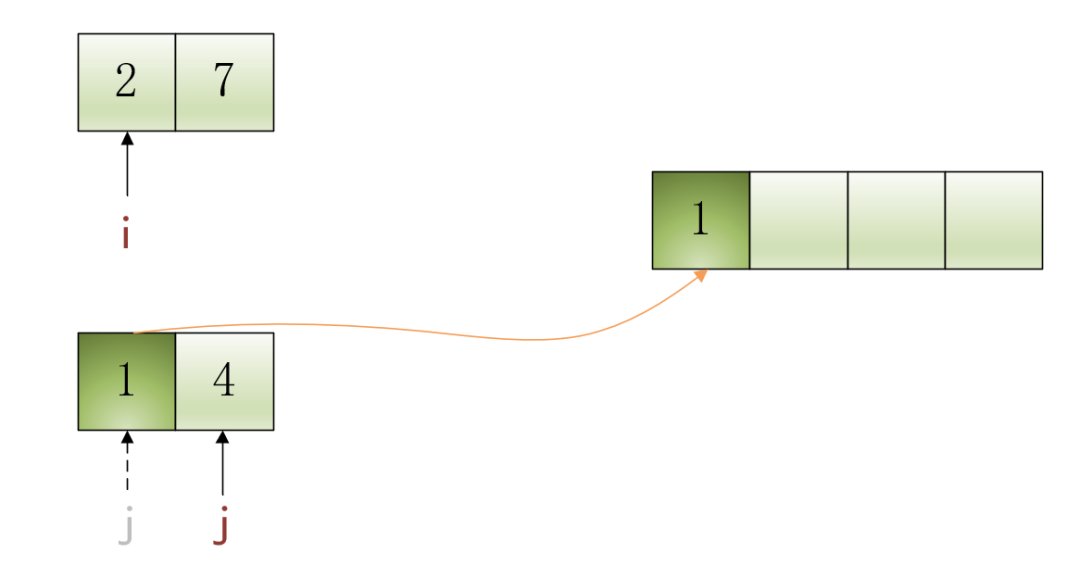
?第2步：當(dāng)前i指向的元素是2，j指向的元素是4，比較i和j指向的元素哪個(gè)更小，由于2<4，所以將i指向的元素2填入結(jié)果數(shù)組中，并將i自增1，效果如下圖所示：

?第3步：當(dāng)前i指向的元素是7，j指向的元素是4，比較i和j指向的元素哪個(gè)更小，由于7>4，所以將j指向的元素4填入結(jié)果數(shù)組中，并將j自增1，效果如下圖所示：

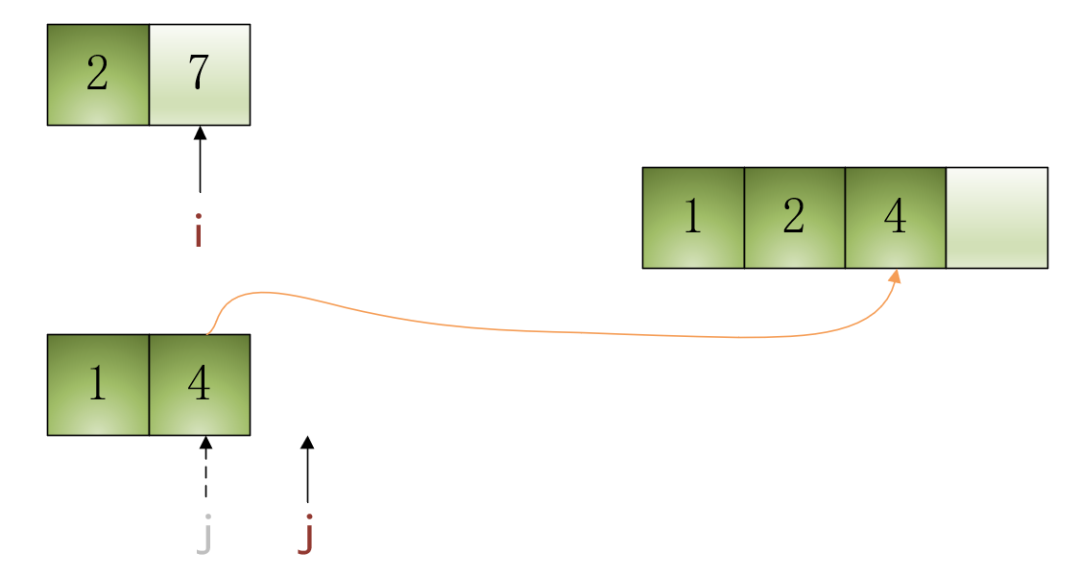
?第4步：當(dāng)前i指向的元素是7，第2個(gè)子數(shù)組中的元素已經(jīng)遍歷完了，所以直接遍歷第1個(gè)子數(shù)組即可，即將i指向的元素7填入結(jié)果數(shù)組收納柜，并將i自增1，效果如下圖所示：

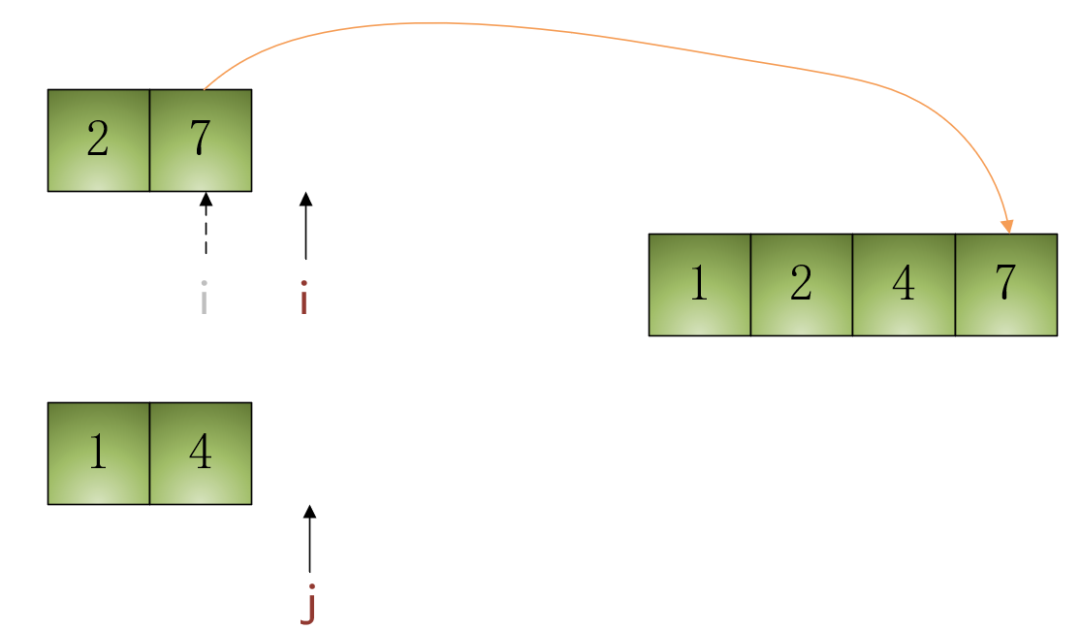
知道了如何合并兩個(gè)有序數(shù)組為一個(gè)大的有序數(shù)組之后，我們就可以完成子問(wèn)題的合并了。

繼續(xù)看在處理細(xì)節(jié)2時(shí)引入的例子：1.1.1組、1.1.2組、1.2.1組、1.2.2組、2.1.1組、2.1.2組、2.2.1組、2.2.2組中僅包含1個(gè)元素，相當(dāng)于子問(wèn)題已經(jīng)得到解決，現(xiàn)在需要合并子問(wèn)題了：

?將1.1.1組、1.1.2組中的有序數(shù)組合并，使1.1組成為有序數(shù)組；

?將1.2.1組、1.2.2組中的有序數(shù)組合并，使1.2組成為有序數(shù)組；

?將2.1.1組、2.1.2組中的有序數(shù)組合并，使2.1組成為有序數(shù)組；

?將2.2.1組、2.2.2組中的有序數(shù)組合并，使2.2組成為有序數(shù)組；

如下圖所示：

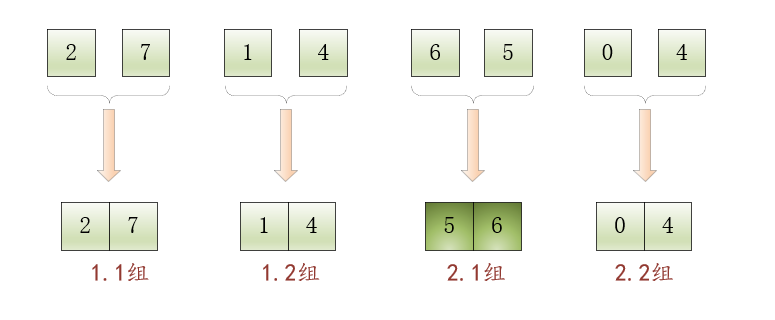
小貼士：

我們將2.1組的顏色加重，以表明組中的元素順序進(jìn)行了重排。

現(xiàn)在1.1組、1.2組、2.1組、2.2組分別是4個(gè)有序數(shù)組，可以繼續(xù)合并子問(wèn)題：

?將1.1組、1.2組中的有序數(shù)組合并，使1組成為有序數(shù)組；

?將2.1組、2.2組中的有序數(shù)組合并，使2組成為有序數(shù)組；

如下圖所示：

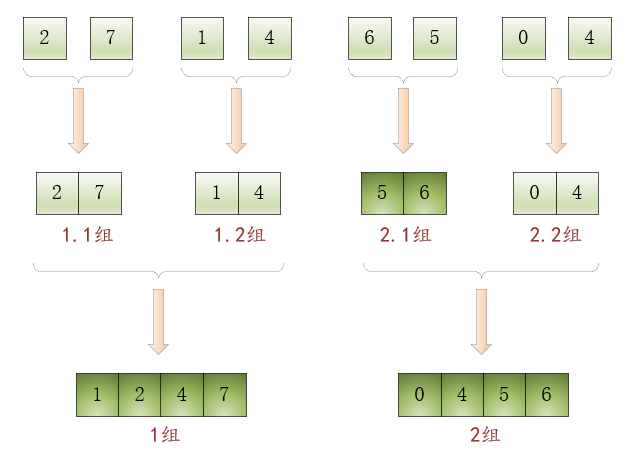
現(xiàn)在1組和2組分別是兩個(gè)有序數(shù)組，可以繼續(xù)合并子問(wèn)題：

?將1組和2組中的有序數(shù)組合并為一個(gè)有序數(shù)組。如下圖所示：

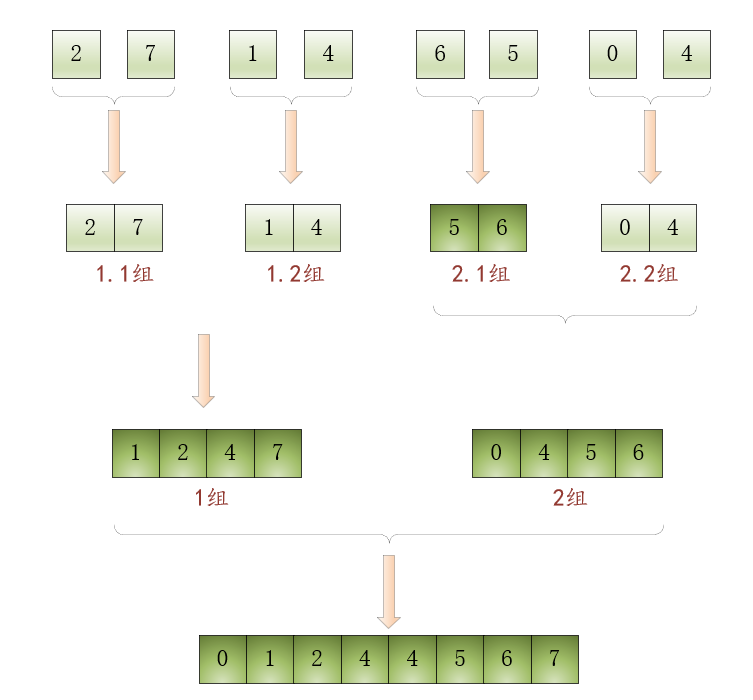
至此，最初排序包含8個(gè)元素的數(shù)組的原始問(wèn)題就得到了解決！

好了，這個(gè)算法的流程就描述完了。相信絕大部分小伙伴還是可以輕松理解上述歸并排序的算法流程的，說(shuō)起來(lái)也可以頭頭是道，但是一旦落實(shí)到筆上，就有點(diǎn)心有余而力不足的趕腳了，下面就來(lái)分析一下到底是哪里難住了我們~

Talk is cheap, show me the code

實(shí)現(xiàn)算法的語(yǔ)言并不是重點(diǎn)，我們下邊將以Java為例，來(lái)看看如何寫(xiě)代碼來(lái)實(shí)現(xiàn)歸并排序。

首先我們是要寫(xiě)一個(gè)用于排序的函數(shù)，就把它命名為mergeSort吧，該函數(shù)用于對(duì)一個(gè)存儲(chǔ)整數(shù)的int數(shù)組進(jìn)行排序，我想100%的小伙伴能完成下面代碼的編寫(xiě)：

public void mergeSort(int[] arr) {
}

如果int數(shù)組arr中沒(méi)有任何元素或者僅包含1個(gè)元素，那壓根兒就不用排序了，我猜90%的同學(xué)可以把下述校驗(yàn)參數(shù)的代碼寫(xiě)出來(lái)：

public void mergeSort(int[] arr) {    if (arr.length <= 1)        return;}

小貼士：

校驗(yàn)參數(shù)十分重要，是展開(kāi)后續(xù)過(guò)程的第一步，還是有很大一部分同學(xué)著急后續(xù)實(shí)現(xiàn)而忘記校驗(yàn)參數(shù)的。

下邊到了真正精彩的地方了！

我們需要把數(shù)組分成兩半，然后分別進(jìn)行排序。這里出現(xiàn)了歸并排序的一個(gè)糾結(jié)點(diǎn)：

?糾結(jié)點(diǎn)：?拆分出的子數(shù)組應(yīng)該存儲(chǔ)到哪里？

之所以說(shuō)是一個(gè)糾結(jié)點(diǎn)，是因?yàn)榭梢杂?種實(shí)現(xiàn)思路：

?思路1：為每個(gè)子數(shù)組都創(chuàng)建一個(gè)新的存儲(chǔ)空間來(lái)存儲(chǔ)它們。

?思路2：還使用原數(shù)組保存子數(shù)組，使用額外的下標(biāo)變量將其區(qū)分開(kāi)即可。

很顯然思路2比思路1更省存儲(chǔ)空間，但思路1可能更簡(jiǎn)單。我們接下來(lái)分別實(shí)現(xiàn)一下思路1和思路2。

思路1 如何實(shí)現(xiàn)

首先我們需要把原數(shù)組切成兩半，然后創(chuàng)建兩個(gè)新數(shù)組，并將原數(shù)組中對(duì)應(yīng)的元素填入到新數(shù)組中，這個(gè)代碼也并不難寫(xiě)，如下所示：

public void mergeSort(int[] arr) {    if (arr.length <= 1)        return;    int mid = (0 + arr.length-1)/2;
    int[] a1 = new int[mid+1];    int[] a2 = new int[arr.length-1-mid];
    copyArr(arr, 0, mid, a1);    copyArr(arr, mid+1, arr.length-1, a2);}

首先我們需要計(jì)算中間元素的下標(biāo)，用初始元素下標(biāo)（例子中就是0）和末尾元素下標(biāo)（例子中就是arr.length-1）的加和除以2即可得到中間元素的下標(biāo)：

int mid = (0 + arr.length-1)/2;

然后創(chuàng)建兩個(gè)數(shù)組a1和a2：

?a1中存放原數(shù)組中下標(biāo)0到mid的元素，共mid+1個(gè)元素。?a2中存放原數(shù)組中下標(biāo)mid+1到arr.length-1的元素，共(arr.length-1) - (mid+1) + 1，也就是arr.length-1-mid個(gè)元素。

然后將原數(shù)組中下標(biāo)0到mid的元素復(fù)制到新數(shù)組a1中，將原數(shù)組中下標(biāo)mid+1到arr.length-1的元素復(fù)制到新數(shù)組a2中。copyArr是我們自己創(chuàng)建的一個(gè)復(fù)制數(shù)組元素的工具方法（工具方法十分簡(jiǎn)單，就不多嘮叨了）：

/** * 將源數(shù)組中指定下標(biāo)的元素復(fù)制到目標(biāo)數(shù)組中 * @param source    源數(shù)組 * @param low       源數(shù)組初始下標(biāo) * @param high      源數(shù)組末尾下標(biāo) * @param dest      目標(biāo)數(shù)組 */private void copyArr(int[] source, int low, int high, int[] dest) {    for (int i=low; i <= high; i++) {        dest[i-low] = source[i];    }}

然后我們就應(yīng)該：

?步驟1：給一個(gè)子數(shù)組進(jìn)行排序；

?步驟2：給另一個(gè)子數(shù)組進(jìn)行排序；

?步驟3：將步驟1和步驟2的得到的兩個(gè)有序子數(shù)組合并為1個(gè)有序數(shù)組。

因?yàn)橛?個(gè)步驟，所以我們需要定義3個(gè)函數(shù)，但由于步驟1和步驟2其實(shí)只是對(duì)某個(gè)數(shù)組進(jìn)行排序，所以此時(shí)我們可以遞歸調(diào)用mergeSort函數(shù)即可。

對(duì)于步驟3，我們可以新定義一個(gè)merge方法來(lái)完成將兩個(gè)子數(shù)組合并為一個(gè)有序數(shù)組的功能，那么現(xiàn)在mergeSort函數(shù)就變成了這樣：

public void mergeSort(int[] arr) {    if (arr.length <= 1)        return;    int mid = (arr.length-1)/2;
    int[] a1 = new int[mid+1];    int[] a2 = new int[arr.length-1-mid];
    copyArr(arr, 0, mid, a1);    copyArr(arr, mid+1, arr.length-1, a2);
    mergeSort(a1);    mergeSort(a2);
    merge(a1, a2, arr);}

好了，現(xiàn)在mergeSort函數(shù)就已經(jīng)寫(xiě)完了，接下來(lái)就只需實(shí)現(xiàn)merge方法即可。merge方法用于將兩個(gè)有序數(shù)組合并為一個(gè)有序數(shù)組，所以它的原型應(yīng)該被定義為：

private void merge(int[] s1, int[] s2, int[] dest) {
}

其中s1和s2是兩個(gè)子數(shù)組，dest是目標(biāo)數(shù)組。

下邊需要定義幾個(gè)變量：

?i表示第1個(gè)子數(shù)組的下標(biāo)，初始指向第1個(gè)子數(shù)組的開(kāi)頭元素，也就是0。

?j表示第2個(gè)子數(shù)組的下標(biāo)，初始指向第2個(gè)子數(shù)組的開(kāi)頭元素，也就是0。

?pos表示目前要填充目標(biāo)數(shù)組哪個(gè)下標(biāo)的元素，初始為0。

我們需要將目標(biāo)數(shù)組填滿，所以引入一個(gè)for循環(huán)，從目標(biāo)數(shù)組開(kāi)頭元素開(kāi)始，直到最后一個(gè)元素為止。代碼如下所示：

private void merge(int[] s1, int[] s2, int[] dest) {    int i = 0;    int j = 0;
    for (int pos = 0; pos < dest.length; pos++) {        // 這里寫(xiě)入填充內(nèi)容    } }

下邊的任務(wù)就是填充for循環(huán)中的內(nèi)容了，我們需要：

?比較s1[i]和s2[j]的大小：如果s1[i]較小，則把s1[i]填入dest[pos]中，并將i自增1；如果s2[j]較小，則把s2[j]填入dest[pos]中，并把j自增1。

那么代碼就可以寫(xiě)成這樣：

private void merge(int[] s1, int[] s2, int[] dest) {    int i = 0;    int j = 0;
    for (int pos = 0; pos < dest.length; pos++) {        if (s1[i] <= s2[j]) {            dest[pos] = s1[i++];        } else {            dest[pos] = s2[j++];        }    } }

上述代碼忽略了一個(gè)最最重要的情況：如果s1先被遍歷完，也就是i為s1.length時(shí)，接下來(lái)就不能訪問(wèn)s1[i]了，否則會(huì)拋出數(shù)組越界異常；如果s2先被遍歷完，也就是j為s2.length時(shí)，接下來(lái)也不能訪問(wèn)s2[j]了，否則也會(huì)拋出數(shù)組越界異常。

忘記邊界條件在編碼實(shí)現(xiàn)算法時(shí)是極其容易出現(xiàn)，并且導(dǎo)致錯(cuò)誤的問(wèn)題。為簡(jiǎn)單起見(jiàn)，我們可以先考慮邊界條件，然后再處理通用內(nèi)容。在本例中，我們可以先處理一下s1遍歷完以及s2遍歷完的情況，然后再比較s1[i]和s2[j]的大小，如下所示：

private void merge(int[] s1, int[] s2, int[] dest) {    int i = 0;    int j = 0;
    for (int pos = 0; pos < dest.length; pos++) {        //如果s1已經(jīng)遍歷完，直接把s2[j]復(fù)制給dest[pos]，并給j自增1        if (i == s1.length){            dest[pos] = s2[j++];        }        //如果s2已經(jīng)遍歷完，直接把s1[i]復(fù)制給dest[pos]，并給i自增1        else if (j == s2.length) {            dest[pos] = s1[i++];        }        //以下是正常情況下的比較        else if (s1[i] <= s2[j]) {            dest[pos] = s1[i++];        } else {            dest[pos] = s2[j++];        }    }}

小貼士：

可以看到，增加判斷邊界條件的代碼時(shí)，代碼量會(huì)增大一倍甚至更多，我們之后可以介紹以下如何使用哨兵來(lái)顯著減少代碼量。

這樣，采用思路1，也就是單獨(dú)為子數(shù)組分配存儲(chǔ)空間的方式實(shí)現(xiàn)歸并排序的過(guò)程我們嘮叨完了，再來(lái)看一下采用思路2如何實(shí)現(xiàn)。

思路2 如何實(shí)現(xiàn)

思路1的弊病其實(shí)很明顯，就是每次調(diào)用mergeSort函數(shù)時(shí)，如果待排序數(shù)組中包含大于1個(gè)的元素，那就需要拆分成2個(gè)子數(shù)組，需要額外的為這兩個(gè)子數(shù)組分配存儲(chǔ)空間。

如果我們不想付出這些額外的成本，直接使用原數(shù)組來(lái)存儲(chǔ)子數(shù)組，那么在對(duì)子數(shù)組進(jìn)行排序時(shí)就不得不指定該子數(shù)組對(duì)應(yīng)的起始下標(biāo)和結(jié)束下標(biāo)是什么，所以我們不得不再定義一個(gè)用于排序子數(shù)組的函數(shù)，我們可以把它稱作mergeSort0，該函數(shù)原型如下所示：

private void mergeSort0(int[] arr, int low, int high) {
}

其中arr是原始數(shù)組，low指的是子數(shù)組的起始下標(biāo)，high指的是子數(shù)組的結(jié)束下標(biāo)。

既然子數(shù)組的形式變成了原始數(shù)組+起始和結(jié)束下標(biāo)的形式，那相應(yīng)的把兩個(gè)有序子數(shù)組合并為一個(gè)有序數(shù)組的merge函數(shù)的參數(shù)也需要變一下了。

我們?cè)诓鸱帜硞€(gè)數(shù)組為兩個(gè)子數(shù)組時(shí)，是采用下邊的方法進(jìn)行拆分的：

?從數(shù)組開(kāi)頭的元素到中間元素屬于一個(gè)子數(shù)組

?從中間元素的后一個(gè)元素開(kāi)始，到數(shù)組最后一個(gè)元素屬于另一個(gè)子數(shù)組

我們把被拆分?jǐn)?shù)組開(kāi)頭元素的下標(biāo)稱作low，把中間元素下標(biāo)稱作mid，把末尾元素的下標(biāo)稱作high，那么被拆分出來(lái)的子數(shù)組的下標(biāo)范圍就是：

?low?~?mid?屬于一個(gè)子數(shù)組

?mid+1?~?high屬于一個(gè)子數(shù)組

在合并子數(shù)組時(shí)，我們只需要知道low、mid、high是多少即可知道這兩個(gè)子數(shù)組的下標(biāo)范圍分別是多少，那么merge函數(shù)的原型應(yīng)該長(zhǎng)這樣：

private void merge(int[] arr, int low, int mid, int high) {
}

有了給子數(shù)組排序的函數(shù)mergeSort0和合并有序子數(shù)組的函數(shù)merge，那我們就可以這樣改寫(xiě)mergeSort：

public void mergeSort(int[] arr) {    if (arr.length <= 1)        return;    int mid = (arr.length-1)/2;
    mergeSort0(arr, 0, mid);    mergeSort0(arr, mid+1, arr.length-1);    merge(arr, 0, mid, arr.length-1);}

下邊先來(lái)實(shí)現(xiàn)以下mergeSort0，需要下邊這些步驟：

?校驗(yàn)參數(shù)

?將待排序數(shù)組拆分成兩個(gè)子數(shù)組

?先給1個(gè)子數(shù)組排序

?再給另一個(gè)子數(shù)組排序

?將兩個(gè)已排序的子數(shù)組合并成一個(gè)有序數(shù)組

下邊看一下具體的代碼：

private void mergeSort0(int[] arr, int low, int high) {    // 校驗(yàn)參數(shù)，如果數(shù)組包含元素個(gè)數(shù)不大于1，則不需排序    if (low >= high)        return;
    // 計(jì)算中間元素位置    int mid = (low + high)/2;
    // 給一個(gè)子數(shù)組排序    mergeSort0(arr, low, mid);
    // 給另一個(gè)子數(shù)組排序    mergeSort0(arr, mid+1, high);
    // 將兩個(gè)已排序子數(shù)組合并為一個(gè)有序數(shù)組    merge(arr, low, mid, high);}

這樣mergeSort0就寫(xiě)完了，該看一下merge函數(shù)如何編寫(xiě)了，不過(guò)這時(shí)候會(huì)有一個(gè)巨大的問(wèn)題：子數(shù)組占用原數(shù)組的存儲(chǔ)空間！

比方說(shuō)某個(gè)數(shù)組有4個(gè)元素[2, 7, 1, 4]，它的兩個(gè)子數(shù)組都是有序的，分別是：[2, 7]和[1, 4]，如下圖所示：

如果我們想對(duì)上圖中的兩個(gè)子數(shù)組進(jìn)行合并，由于j指向的元素1小于i指向的元素2，所以會(huì)將1放置在結(jié)果數(shù)組中的首個(gè)元素中，而結(jié)果數(shù)組就是原數(shù)組的話，直接就會(huì)把原數(shù)組的首個(gè)元素2給覆蓋掉！這是萬(wàn)萬(wàn)不能忍的。

為解決上述問(wèn)題，我們需要一個(gè)臨時(shí)的存儲(chǔ)空間來(lái)存儲(chǔ)有序子數(shù)組內(nèi)容，這樣在將結(jié)果寫(xiě)回原數(shù)組時(shí)才不會(huì)破壞子數(shù)組。這個(gè)臨時(shí)的存儲(chǔ)空間可以在merge函數(shù)內(nèi)開(kāi)辟，但是這樣的話每調(diào)用一次merge函數(shù)都需要開(kāi)辟一段臨時(shí)的存儲(chǔ)空間，也可以作為一個(gè)全局變量只申請(qǐng)一次存儲(chǔ)空間。很顯然后者優(yōu)雅一些，我們這里采用后者。

首先我們定義一個(gè)名叫tmp的成員變量：

private int[] tmp;

然后改寫(xiě)以下mergeSort函數(shù)，給tmp數(shù)組分配存儲(chǔ)空間：

public void mergeSort(int[] arr) {    //給全局變量tmp分配存儲(chǔ)空間    tmp = new int[arr.length];
    if (arr.length <= 1)        return;
    int mid = (arr.length-1)/2;
    mergeSort0(arr, 0, mid);    mergeSort0(arr, mid+1, arr.length-1);    merge(arr, 0, mid, arr.length-1);}

然后我們?cè)?code style="box-sizing: border-box;padding: 3px 5px;color: rgb(255, 53, 2);line-height: 1.5;font-family: "Operator Mono", Consolas, Monaco, Menlo, monospace;font-size: 14.4px;background: rgb(248, 245, 236);border-radius: 2px;">merge函數(shù)里就可以使用這個(gè)tmp數(shù)組了（由于在討論思路1的實(shí)現(xiàn)時(shí)已經(jīng)詳細(xì)討論過(guò)merge函數(shù)的實(shí)現(xiàn)，所以我們這里就不花大篇幅討論下邊改版后的merge函數(shù)了）：

private void merge(int arr[], int low, int mid, int high) {    int i = low;    int j = mid+1;
    //將子數(shù)組的內(nèi)容先復(fù)制到tmp數(shù)組中    for (int pos = low; pos <= high; pos++) {        tmp[pos] = arr[pos];    }
    for (int pos = low; pos <= high; pos++) {        if (i == mid+1) {            arr[pos] = tmp[j++];        }        else if (j == high + 1) {            arr[pos] = tmp[i++];        }        else if (tmp[i] <= tmp[j]) {            arr[pos] = tmp[i++];        } else {            arr[pos] = tmp[j++];        }    }}

好的，大功告成！

再回頭看一下我們是不是還可以優(yōu)化什么地方呢？

大家如果仔細(xì)觀察一下mergeSort和mergeSort0兩個(gè)函數(shù)的代碼就會(huì)發(fā)現(xiàn)，它們的功能是極其類似的！只不過(guò)mergeSort里指定的開(kāi)始元素為恒定的0，結(jié)束元素為恒定的arr.length-1，而mergeSort0里用變量low和high來(lái)替代。當(dāng)程序中出現(xiàn)了相同功能的代碼時(shí)，一定要看一下能不能將功能相同的代碼合并起來(lái)！?在本例中，mergeSort中的代碼起始和調(diào)用一次mergeSort0(arr, 0, arr.length-1)是相同的，所以我們?cè)倬?jiǎn)一下mergeSort函數(shù)：

public void mergeSort(int[] arr) {    tmp = new int[arr.length];    mergeSort0(arr, 0, arr.length-1);}

好的，這回才算大功告成了！

總結(jié)回顧

歸并排序算法極其簡(jiǎn)單，但它背后所體現(xiàn)的分治思想卻是那么的重要，我們下邊再來(lái)梳理一下分治思想，大概分為3步：

1.分（Divide）：即將一個(gè)大問(wèn)題拆分為若干個(gè)小問(wèn)題（在歸并排序中就是將待排序數(shù)組拆分成2個(gè)子數(shù)組）。2.治（Conquer）：使用遞歸的形式繼續(xù)拆解小問(wèn)題，直到問(wèn)題小到可以很輕松的解決（在歸并排序中就是將子數(shù)組拆到只剩1個(gè)元素，那1個(gè)元素就肯定是有序的）。3.合（Combine）：將已解決的子問(wèn)題合并起來(lái)，從而解決大問(wèn)題（在歸并排序中就是將已排序的子數(shù)組合并成一個(gè)有序數(shù)組）。

另外，在具體的歸并排序中，大家需要注意下述問(wèn)題：

?進(jìn)行參數(shù)校驗(yàn)十分必要

?在進(jìn)行循環(huán)時(shí)注意邊界條件的判斷，可以先將特殊情況寫(xiě)清楚后，再寫(xiě)通用情況

?如何計(jì)算數(shù)組的中間元素以及如何劃分子數(shù)組？選取(起始元素下標(biāo)+結(jié)束元素下標(biāo))/2的形式和直接用數(shù)組長(zhǎng)度/2有什么區(qū)別。

?如何存儲(chǔ)子數(shù)組？是用額外的存儲(chǔ)空間，還是在原數(shù)組中保存加上起始和結(jié)束下標(biāo)呢？

?在遇到功能相同的代碼時(shí)注意合并代碼

小貼士：我們之前在講MySQL的索引合并的時(shí)候用到了merge方法，大家還記得嗎？。

好的，以上就是關(guān)于實(shí)現(xiàn)歸并函數(shù)時(shí)的一些思考，希望可以對(duì)大家有所幫助。

— 本文結(jié)束 —

●?漫談設(shè)計(jì)模式在 Spring 框架中的良好實(shí)踐

●?顛覆微服務(wù)認(rèn)知：深入思考微服務(wù)的七個(gè)主流觀點(diǎn)

●?人人都是 API 設(shè)計(jì)者

●?一文講透微服務(wù)下如何保證事務(wù)的一致性

●?要黑盒測(cè)試微服務(wù)內(nèi)部服務(wù)間調(diào)用，我該如何實(shí)現(xiàn)？

在看點(diǎn)這里