深入理解圖注意力機(jī)制

圖卷積網(wǎng)絡(luò)(GCN)告訴我們，將局部的圖結(jié)構(gòu)和節(jié)點(diǎn)特征結(jié)合可以在節(jié)點(diǎn)分類任務(wù)中獲得不錯(cuò)的表現(xiàn)。美中不足的是GCN結(jié)合鄰近節(jié)點(diǎn)特征的方式和圖的結(jié)構(gòu)依依相關(guān)，這局限了訓(xùn)練所得模型在其他圖結(jié)構(gòu)上的泛化能力。

Graph Attention Network (GAT)提出了用注意力機(jī)制對(duì)鄰近節(jié)點(diǎn)特征加權(quán)求和。鄰近節(jié)點(diǎn)特征的權(quán)重完全取決于節(jié)點(diǎn)特征，獨(dú)立于圖結(jié)構(gòu)。

在這個(gè)教程里我們將：

難度：★★★★? （需要對(duì)圖神經(jīng)網(wǎng)絡(luò)訓(xùn)練和Pytorch有基本了解）

在GCN里引入注意力機(jī)制

GAT和GCN的核心區(qū)別在于如何收集并累和距離為1的鄰居節(jié)點(diǎn)的特征表示。在GCN里，一次圖卷積操作包含對(duì)鄰節(jié)點(diǎn)特征的標(biāo)準(zhǔn)化求和：

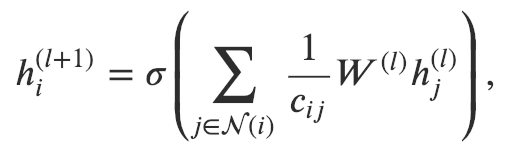
其中 是對(duì)節(jié)點(diǎn)距離為1鄰節(jié)點(diǎn)的集合。我們通常會(huì)加一條連接節(jié)點(diǎn) 和它自身的邊使得 本身也被包括在里。 是一個(gè)基于圖結(jié)構(gòu)的標(biāo)準(zhǔn)化常數(shù)； 是一個(gè)激活函數(shù) （GCN使用了ReLU）； 是節(jié)點(diǎn)特征轉(zhuǎn)換的權(quán)重矩陣，被所有節(jié)點(diǎn)共享。由于 和圖的機(jī)構(gòu)相關(guān)，使得在一張圖上學(xué)習(xí)到的GCN模型比較難直接應(yīng)用到另一張圖上。解決這一問題的方法有很多，比如GraphSAGE提出了一種采用相同節(jié)點(diǎn)特征更新規(guī)則的模型，唯一的區(qū)別是他們將 設(shè)為了 。

圖注意力模型GAT用注意力機(jī)制替代了圖卷積中固定的標(biāo)準(zhǔn)化操作。以下圖和公式定義了如何對(duì)第 層節(jié)點(diǎn)特征做更新得到第 層節(jié)點(diǎn)特征：

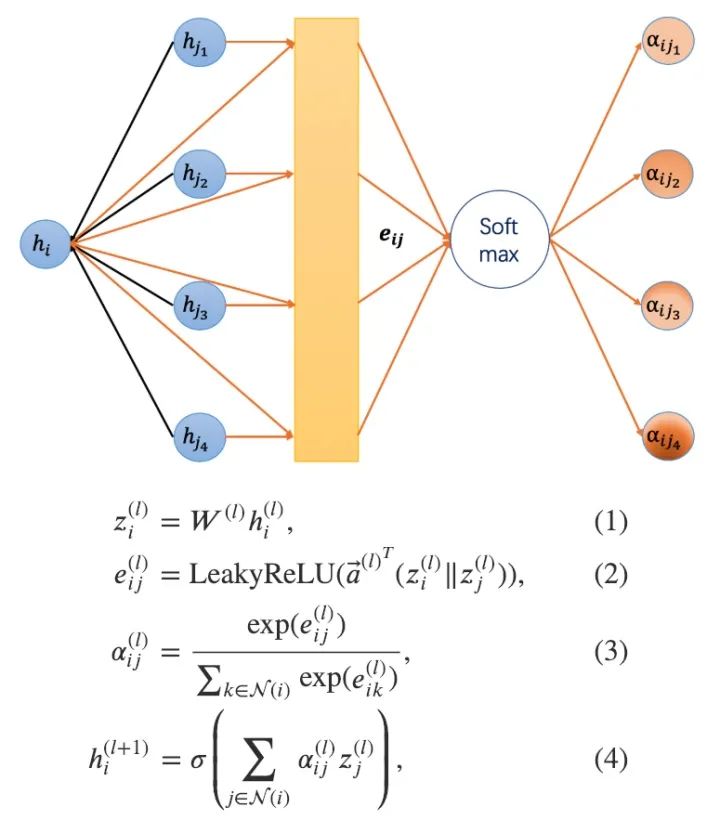
注意力網(wǎng)絡(luò)示意圖和更新公式

對(duì)于上述公式的一些解釋：

出于簡(jiǎn)潔的考量，在本教程中，我們選擇省略了一些論文中的細(xì)節(jié)，如dropout, skip connection等等。感興趣的讀者們歡迎參閱文末鏈接的模型完整實(shí)現(xiàn)。本質(zhì)上，GAT只是將原本的標(biāo)準(zhǔn)化常數(shù)替換為使用注意力權(quán)重的鄰居節(jié)點(diǎn)特征聚合函數(shù)。

GAT的DGL實(shí)現(xiàn)

以下代碼給讀者提供了在DGL里實(shí)現(xiàn)一個(gè)GAT層的總體印象。別擔(dān)心，我們會(huì)將以下代碼拆分成三塊，并逐塊講解每塊代碼是如何實(shí)現(xiàn)上面的一條公式。

import torchimport torch.nn as nnimport torch.nn.functional as F
class GATLayer(nn.Module):    def __init__(self, g, in_dim, out_dim):        super(GATLayer, self).__init__()        self.g = g        # 公式 (1)        self.fc = nn.Linear(in_dim, out_dim, bias=False)        # 公式 (2)        self.attn_fc = nn.Linear(2 * out_dim, 1, bias=False)
    def edge_attention(self, edges):        # 公式 (2) 所需，邊上的用戶定義函數(shù)        z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1)        a = self.attn_fc(z2)        return {'e' : F.leaky_relu(a)}
    def message_func(self, edges):        # 公式 (3), (4)所需，傳遞消息用的用戶定義函數(shù)        return {'z' : edges.src['z'], 'e' : edges.data['e']}
    def reduce_func(self, nodes):        # 公式 (3), (4)所需, 歸約用的用戶定義函數(shù)        # 公式 (3)        alpha = F.softmax(nodes.mailbox['e'], dim=1)        # 公式 (4)        h = torch.sum(alpha * nodes.mailbox['z'], dim=1)        return {'h' : h}
    def forward(self, h):        # 公式 (1)        z = self.fc(h)        self.g.ndata['z'] = z        # 公式 (2)        self.g.apply_edges(self.edge_attention)        # 公式 (3) & (4)        self.g.update_all(self.message_func, self.reduce_func)        return self.g.ndata.pop('h')

實(shí)現(xiàn)公式(1)

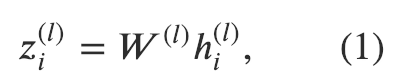
第一個(gè)公式相對(duì)比較簡(jiǎn)單。線性變換非常常見。在PyTorch里，我們可以通過torch.nn.Linear很方便地實(shí)現(xiàn)。

實(shí)現(xiàn)公式(2)

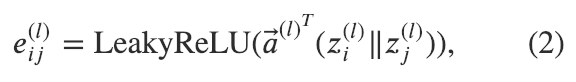
原始注意力權(quán)重 是基于一對(duì)鄰近節(jié)點(diǎn) 和 的表示計(jì)算得到。我們可以把注意力權(quán)重 看成在 i->j 這條邊的數(shù)據(jù)。因此，在DGL里，我們可以使用 g.apply_edges 這一API來調(diào)用邊上的操作，用一個(gè)邊上的用戶定義函數(shù)來指定具體操作的內(nèi)容。我們?cè)谟脩舳x函數(shù)里實(shí)現(xiàn)了公式（2）的操作：

    def edge_attention(self, edges):        # 公式 (2) 所需，邊上的用戶定義函數(shù)        z2 = torch.cat([edges.src['z'], edges.dst['z']], dim=1)        a = self.attn_fc(z2)        return {'e' : F.leaky_relu(a)}

公式中的點(diǎn)積同樣借由PyTorch的一個(gè)線性變換 attn_fc 實(shí)現(xiàn)。注意 apply_edges 會(huì)把所有邊上的數(shù)據(jù)打包為一個(gè)張量，這使得拼接和點(diǎn)積可以并行完成。

實(shí)現(xiàn)公式(3)和(4)

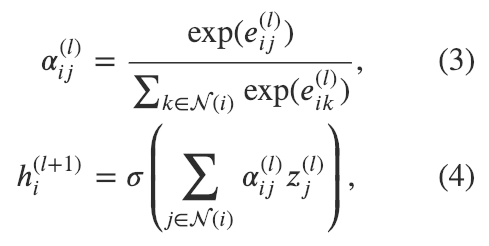
類似GCN，在DGL里我們使用update_all API來觸發(fā)所有節(jié)點(diǎn)上的消息傳遞函數(shù)。update_all接收兩個(gè)用戶自定義函數(shù)作為參數(shù)。message_function發(fā)送了兩種張量作為消息：消息原節(jié)點(diǎn)的表示以及每條邊上的原始注意力權(quán)重。reduce_function隨后進(jìn)行了兩項(xiàng)操作：

這兩項(xiàng)操作都先從節(jié)點(diǎn)的 mailbox 獲取了數(shù)據(jù)，隨后在數(shù)據(jù)的第二維（ dim = 1 ) 上進(jìn)行了運(yùn)算。注意數(shù)據(jù)的第一維代表了節(jié)點(diǎn)的數(shù)量，第二維代表了每個(gè)節(jié)點(diǎn)收到消息的數(shù)量。

    def reduce_func(self, nodes):        # 公式 (3), (4)所需, 歸約用的用戶定義函數(shù)        # 公式 (3)        alpha = F.softmax(nodes.mailbox['e'], dim=1)        # 公式 (4)        h = torch.sum(alpha * nodes.mailbox['z'], dim=1)        return {'h' : h}

多頭注意力 (Multi-head attention)

神似卷積神經(jīng)網(wǎng)絡(luò)里的多通道，GAT引入了多頭注意力來豐富模型的能力和穩(wěn)定訓(xùn)練的過程。每一個(gè)注意力的頭都有它自己的參數(shù)。如何整合多個(gè)注意力機(jī)制的輸出結(jié)果一般有兩種方式：

• 拼接：
• 平均：

以上式子中是注意力頭的數(shù)量。作者們建議對(duì)中間層使用拼接對(duì)最后一層使用求平均。

我們之前有定義單頭注意力的GAT層，它可作為多頭注意力GAT層的組建單元：

class MultiHeadGATLayer(nn.Module):    def __init__(self, g, in_dim, out_dim, num_heads, merge='cat'):        super(MultiHeadGATLayer, self).__init__()        self.heads = nn.ModuleList()        for i in range(num_heads):            self.heads.append(GATLayer(g, in_dim, out_dim))        self.merge = merge
    def forward(self, h):        head_outs = [attn_head(h) for attn_head in self.heads]        if self.merge == 'cat':            # 對(duì)輸出特征維度（第1維）做拼接            return torch.cat(head_outs, dim=1)        else:            # 用求平均整合多頭結(jié)果            return torch.mean(torch.stack(head_outs))

在Cora數(shù)據(jù)集上訓(xùn)練一個(gè)GAT模型

Cora是經(jīng)典的文章引用網(wǎng)絡(luò)數(shù)據(jù)集。Cora圖上的每個(gè)節(jié)點(diǎn)是一篇文章，邊代表文章和文章間的引用關(guān)系。每個(gè)節(jié)點(diǎn)的初始特征是文章的詞袋（Bag of words）表示。其目標(biāo)是根據(jù)引用關(guān)系預(yù)測(cè)文章的類別（比如機(jī)器學(xué)習(xí)還是遺傳算法）。在這里，我們定義一個(gè)兩層的GAT模型：

class GAT(nn.Module):    def __init__(self, g, in_dim, hidden_dim, out_dim, num_heads):        super(GAT, self).__init__()        self.layer1 = MultiHeadGATLayer(g, in_dim, hidden_dim, num_heads)        # 注意輸入的維度是 hidden_dim * num_heads 因?yàn)槎囝^的結(jié)果都被拼接在了        # 一起。此外輸出層只有一個(gè)頭。        self.layer2 = MultiHeadGATLayer(g, hidden_dim * num_heads, out_dim, 1)
    def forward(self, h):        h = self.layer1(h)        h = F.elu(h)        h = self.layer2(h)        return h

我們使用DGL自帶的數(shù)據(jù)模塊加載Cora數(shù)據(jù)集。

from dgl import DGLGraphfrom dgl.data import citation_graph as citegrh
def load_cora_data():    data = citegrh.load_cora()    features = torch.FloatTensor(data.features)    labels = torch.LongTensor(data.labels)    mask = torch.ByteTensor(data.train_mask)    g = DGLGraph(data.graph)    return g, features, labels, mask

模型訓(xùn)練的流程和GCN教程里的一樣。

import timeimport numpy as npg, features, labels, mask = load_cora_data()
# 創(chuàng)建模型net = GAT(g,           in_dim=features.size()[1],           hidden_dim=8,           out_dim=7,           num_heads=8)print(net)
# 創(chuàng)建優(yōu)化器optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)
# 主流程dur = []for epoch in range(30):    if epoch >=3:        t0 = time.time()
    logits = net(features)    logp = F.log_softmax(logits, 1)    loss = F.nll_loss(logp[mask], labels[mask])
    optimizer.zero_grad()    loss.backward()    optimizer.step()
    if epoch >=3:        dur.append(time.time() - t0)
    print("Epoch {:05d} | Loss {:.4f} | Time(s) {:.4f}".format(            epoch, loss.item(), np.mean(dur)))

可視化并理解學(xué)到的注意力

1、Cora數(shù)據(jù)集

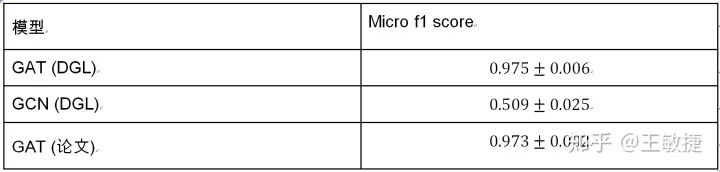
以下表格總結(jié)了GAT論文以及dgl實(shí)現(xiàn)的模型在Cora數(shù)據(jù)集上的表現(xiàn)：

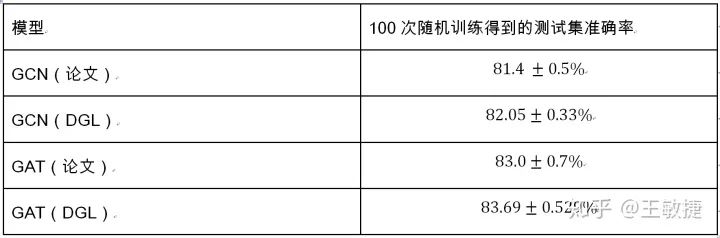
可以看到DGL能完全復(fù)現(xiàn)原論文中的實(shí)驗(yàn)結(jié)果。對(duì)比圖卷積網(wǎng)絡(luò)GCN，GAT在Cora上有2~3個(gè)百分點(diǎn)的提升。

不過，我們的模型究竟學(xué)到了怎樣的注意力機(jī)制呢？

由于注意力權(quán)重與圖上的邊密切相關(guān)，我們可以通過給邊著色來可視化注意力權(quán)重。以下圖片中我們選取了Cora的一個(gè)子圖并且在圖上畫出了GAT模型最后一層的注意力權(quán)重。我們根據(jù)圖上節(jié)點(diǎn)的標(biāo)簽對(duì)節(jié)點(diǎn)進(jìn)行了著色，根據(jù)注意力權(quán)重的大小對(duì)邊進(jìn)行了著色（可參考圖右側(cè)的色條）。

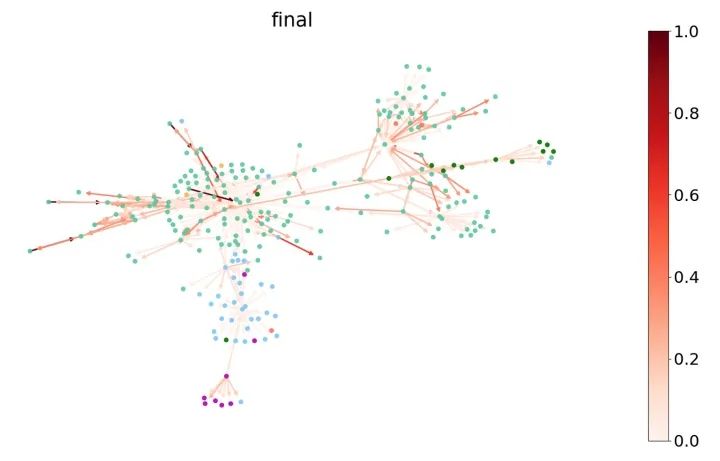
Cora數(shù)據(jù)集上學(xué)習(xí)到的注意力權(quán)重

乍看之下模型似乎學(xué)到了不同的注意力權(quán)重。為了對(duì)注意力機(jī)制有一個(gè)全局觀念，我們衡量了注意力分布的熵。對(duì)于節(jié)點(diǎn)， 構(gòu)成了一個(gè)在鄰節(jié)點(diǎn)上的離散概率分布。它的熵被定義為：

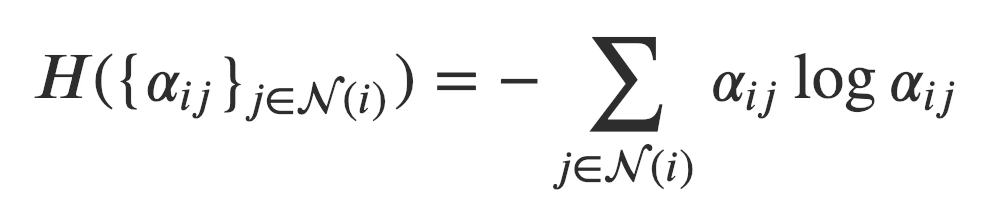
直觀的說，熵低代表了概率高度集中，反之亦然。熵為則所有的注意力都被放在一個(gè)點(diǎn)上。均勻分布具有最高的熵（ ）。在理想情況下，我們想要模型習(xí)得一個(gè)熵較低的分布（即某一、兩個(gè)節(jié)點(diǎn)比其它節(jié)點(diǎn)重要的多）。注意由于節(jié)點(diǎn)的入度不同，它們注意力權(quán)重的分布所能達(dá)到的最大熵也會(huì)不同。

基于圖中所有節(jié)點(diǎn)的熵，我們畫了所有頭注意力的直方圖。

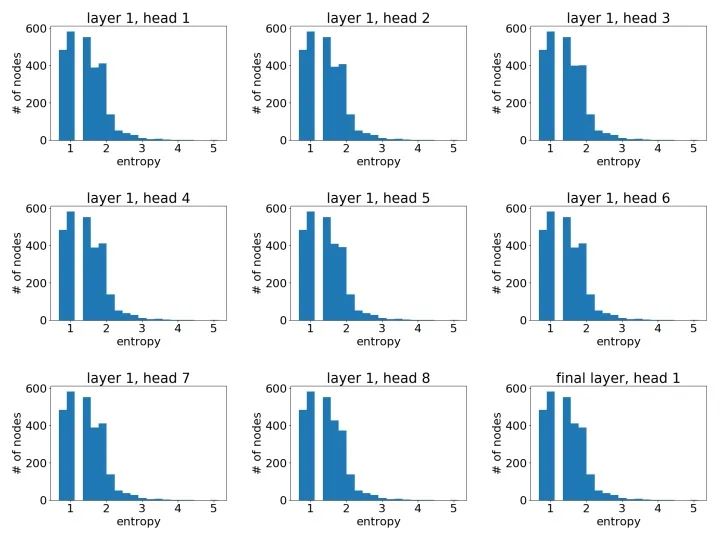
Cora數(shù)據(jù)集上學(xué)到的注意力權(quán)重直方圖

作為參考，下圖是在所有節(jié)點(diǎn)的注意力權(quán)重都是均勻分布的情況下得到的直方圖。

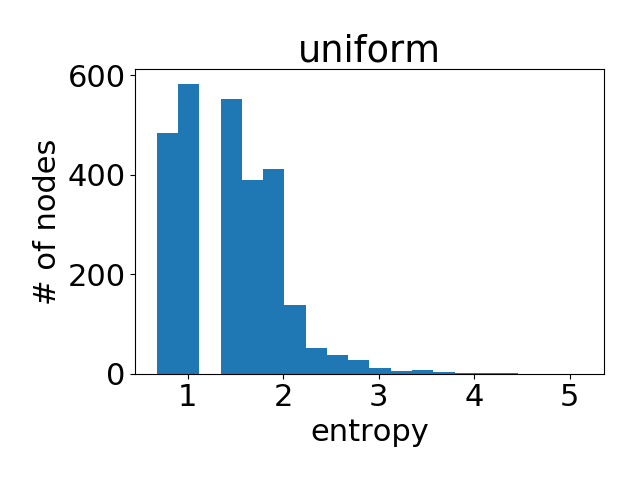
出人意料的，模型學(xué)到的節(jié)點(diǎn)注意力權(quán)重非常接近均勻分布（換言之，所有的鄰節(jié)點(diǎn)都獲得了同等重視）。這在一定程度上解釋了為什么在Cora上GAT的表現(xiàn)和GCN非常接近（在上面表格里我們可以看到兩者的差距平均下來不到）。由于沒有顯著區(qū)分節(jié)點(diǎn)，注意力并沒有那么重要。

這是否說明了注意力機(jī)制沒什么用？不！在接下來的數(shù)據(jù)集上我們觀察到了完全不同的現(xiàn)象。

2、蛋白質(zhì)交互網(wǎng)絡(luò) (PPI)

PPI（蛋白質(zhì)間相互作用）數(shù)據(jù)集包含了24張圖，對(duì)應(yīng)了不同的人體組織。節(jié)點(diǎn)最多可以有121種標(biāo)簽（比如蛋白質(zhì)的一些性質(zhì)、所處位置等）。因此節(jié)點(diǎn)標(biāo)簽被表示為有個(gè)121元素的二元張量。數(shù)據(jù)集的任務(wù)是預(yù)測(cè)節(jié)點(diǎn)標(biāo)簽。

我們使用了20張圖進(jìn)行訓(xùn)練，2張圖進(jìn)行驗(yàn)證，2張圖進(jìn)行測(cè)試。平均下來每張圖有2372個(gè)節(jié)點(diǎn)。每個(gè)節(jié)點(diǎn)有50個(gè)特征，包含定位基因集合、特征基因集合以及免疫特征。至關(guān)重要的是，測(cè)試用圖在訓(xùn)練過程中對(duì)模型完全不可見。這一設(shè)定被稱為歸納學(xué)習(xí)。

我們比較了dgl實(shí)現(xiàn)的GAT和GCN在10次隨機(jī)訓(xùn)練中的表現(xiàn)。模型的超參數(shù)在驗(yàn)證集上進(jìn)行了優(yōu)化。在實(shí)驗(yàn)中我們使用了micro f1 score來衡量模型的表現(xiàn)。

在訓(xùn)練過程中，我們使用了 BCEWithLogitsLoss 作為損失函數(shù)。下圖繪制了GAT和GCN的學(xué)習(xí)曲線；顯然GAT的表現(xiàn)遠(yuǎn)優(yōu)于GCN。

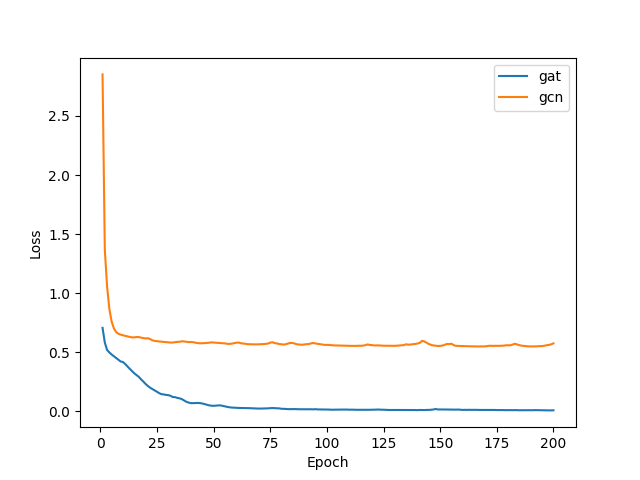
PPI數(shù)據(jù)集上GCN和GAT學(xué)習(xí)曲線比較

像之前一樣，我們可以通過繪制節(jié)點(diǎn)注意力分布之熵的直方圖來有一個(gè)統(tǒng)計(jì)意義上的直觀了解。以下我們基于一個(gè)3層GAT模型中不同模型層不同注意力頭繪制了直方圖。

第一層學(xué)到的注意力：

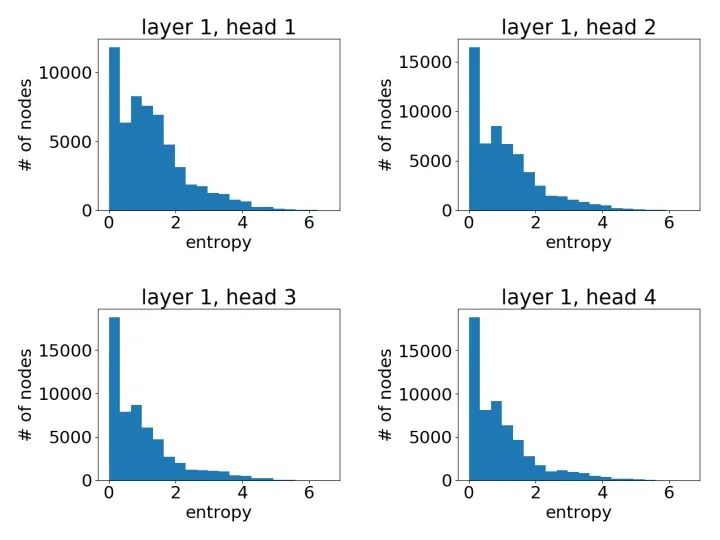
第二層學(xué)到的注意力：

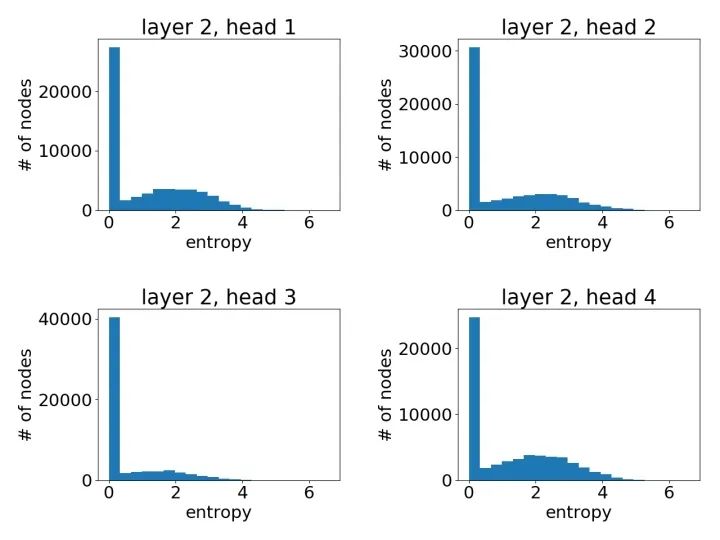
最后一層學(xué)到的注意力：

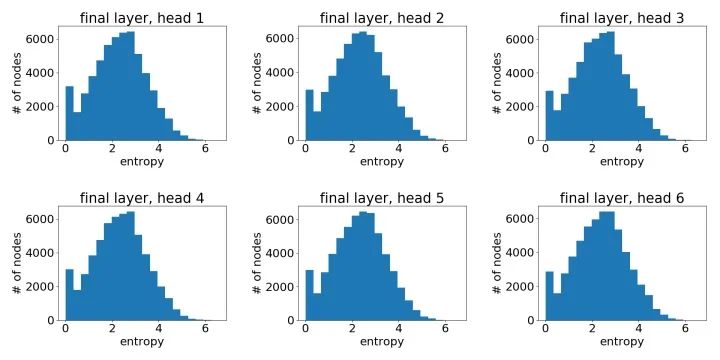
作為參考，下圖是在所有節(jié)點(diǎn)的注意力權(quán)重都是均勻分布的情況下得到的直方圖。

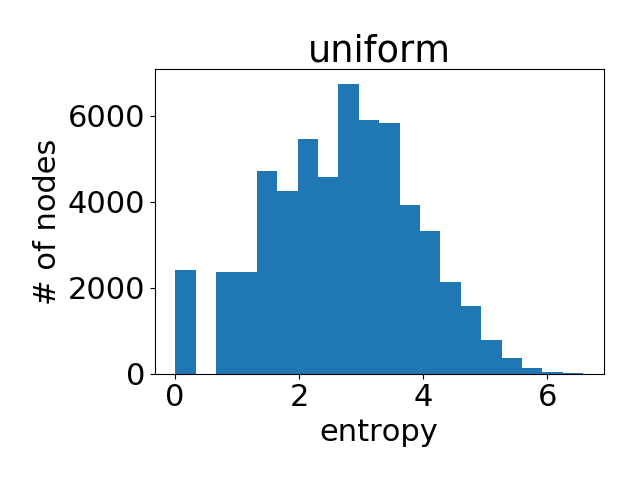
可以很明顯地看到，GAT在PPI上確實(shí)學(xué)到了一個(gè)尖銳的注意力權(quán)重分布。與此同時(shí)，GAT層與層之間的注意力也呈現(xiàn)出一個(gè)清晰的模式：在中間層隨著層數(shù)的增加注意力權(quán)重變得愈發(fā)集中；最后的輸出層由于我們對(duì)不同頭結(jié)果做了平均，注意力分布再次趨近均勻分布。

不同于在Cora數(shù)據(jù)集上非常有限的收益，GAT在PPI數(shù)據(jù)集上較GCN和其它圖模型的變種取得了明顯的優(yōu)勢(shì)（根據(jù)原論文的結(jié)果在測(cè)試集上的表現(xiàn)提升了至少20%）。我們的實(shí)驗(yàn)揭示了GAT學(xué)到的注意力顯著區(qū)別于均勻分布。雖然這值得進(jìn)一步的深入研究，一個(gè)由此而生的假設(shè)是GAT的優(yōu)勢(shì)在于處理更復(fù)雜領(lǐng)域結(jié)構(gòu)的能力。

拓展閱讀

到目前為止我們演示了如何用DGL實(shí)現(xiàn)GAT。簡(jiǎn)介起見，我們忽略了dropout, skip connection等一些細(xì)節(jié)。這些細(xì)節(jié)很常見且獨(dú)立于DGL相關(guān)的概念。有興趣的讀者歡迎參閱完整的代碼實(shí)現(xiàn)。