紅黑樹的理解與 Java 實現(xiàn)
前言 紅黑樹的性質(zhì) 紅黑樹的操作 1. 查找操作 2. 插入操作 3. 刪除操作 Java實現(xiàn) 總結(jié)
前言
前段時間在研究 JDK1.8 的 hashmap 源碼,看到 put 方法的插入環(huán)節(jié),遇到了紅黑樹,不得不停止閱讀源碼的過程,因為還沒掌握紅黑樹是無法完全讀透 hashmap 源碼的。紅黑樹作為一種數(shù)據(jù)結(jié)構(gòu),它被應(yīng)用得非常多,可能很多人不認(rèn)識它,但其實它已經(jīng)在默默為我們的代碼在發(fā)光發(fā)熱。例如,你只要在 Java 中用到 map,基本上就是在用紅黑樹(當(dāng)元素個數(shù)到達(dá)八個時鏈表轉(zhuǎn)紅黑樹)。
PS:在看這篇文章前,必須先了解普通的二叉查找樹和平衡查找樹(AVL)樹、2-3-4樹。不然看起來會非常吃力。
紅黑樹的性質(zhì)
紅黑樹是一種自平衡樹,它也是一顆二叉樹。既然能保持平衡,說明它和 AVL 樹類似,在插入或者刪除時肯定有調(diào)整的過程,只不過這個調(diào)整過程并不像 AVL 樹那樣繁瑣。為何紅黑樹使用得比 AVL 樹更多,就是因為紅黑樹它的調(diào)整過程迅速且簡介。紅黑樹有以下五個特性:
性質(zhì)1:節(jié)點是紅色或黑色 性質(zhì)2:根是黑色 性質(zhì)3:所有葉子都是黑色。葉子是 NIL 節(jié)點,也就是 Null 節(jié)點 性質(zhì)4:如果一個節(jié)點是紅的,則它的兩個兒子都是黑的 性質(zhì)5:從任一節(jié)點到其葉子的所有簡單路徑都包含相同數(shù)目的黑色節(jié)點。
下圖展示了一棵紅黑樹。
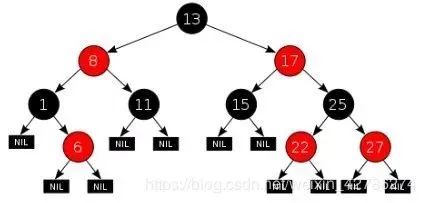
分析:
注意理解上,葉子并不等價于黑色節(jié)點,但是他們的顏色都是黑色。
為何要給節(jié)點指定紅或者黑的顏色?
作者這種設(shè)計,只是為了從編程上達(dá)到一種便利的效果。另外可以讓它們在插入時達(dá)到近似的平衡,并不像 AVL 樹那樣絕對平衡。實際上,紅黑樹是2-3樹的一種變體,某種情況下,它又相當(dāng)于2-3-4樹。因為2-3樹在編程上需要比較多的代碼量,所以誕生了紅黑樹這種巧妙的設(shè)計。通過加了顏色來區(qū)分結(jié)點,這樣編程上就可以當(dāng)成二叉樹來寫程序,不用分別用三個指針表示左、中、右孩子了。
看一下紅黑樹和2-3樹的等價性聯(lián)系
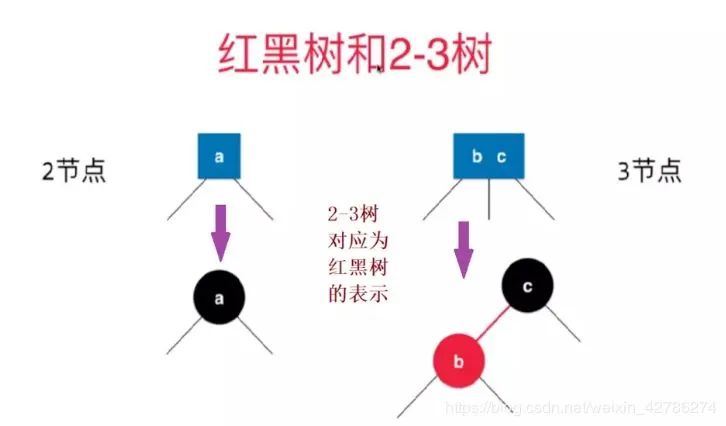
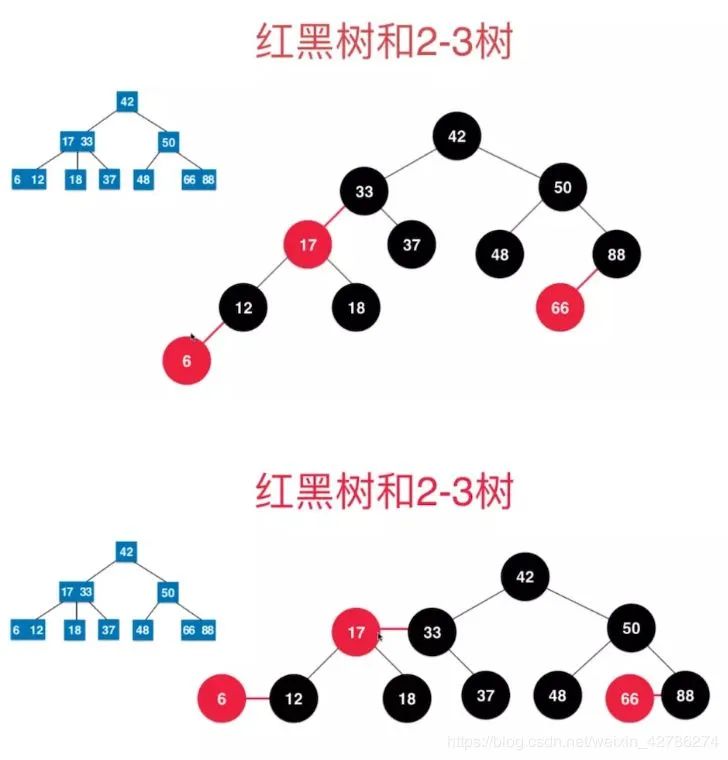
從上面可以看到,把紅色節(jié)點放到與父親齊平,就是2-3樹中的一個2-3節(jié)點。
紅黑樹的操作
數(shù)據(jù)結(jié)構(gòu)的性質(zhì)看完之后,就要掌握它到底會存在哪種操作?例如 hashmap,它最常見的操作就是 get 和 put、擴(kuò)容。同理,紅黑樹也有它的基本操作。因為它本身上也是一棵二叉查找樹,所以重點關(guān)注的操作無非就是查找、插入、刪除。
1. 查找操作
紅黑樹的查找方式很簡單,只要是樹,查找的過程無非就是一個遞歸過程。如果查找的元素小于當(dāng)前節(jié)點,那么查找其左子樹;如果查找的元素大于當(dāng)前元素,則查找其右子樹。
2. 插入操作
插入操作首先需要通過查找操作找到合適的插入點,然后插入新節(jié)點。如果在插入節(jié)點后,發(fā)生了違背紅黑樹特性的情況時,需要對紅黑樹進(jìn)行旋轉(zhuǎn)染色等操作,使其重新滿足特性。
2.1 插入新節(jié)點
為了在插入新節(jié)點時盡可能少的違反紅黑樹特性且更容易調(diào)整紅黑樹,就先將新節(jié)點染成紅色。這樣就只可能會違反特性4。如果這里沒有違反特性4,那么就不需要對紅黑樹進(jìn)行調(diào)整,插入操作完成。
2.2 調(diào)整子樹
那么,在違反了特性4的時候,新節(jié)點的父節(jié)點為紅色節(jié)點。根據(jù)特性2可知,父節(jié)點不是根節(jié)點,則新節(jié)點必有祖父節(jié)點。又根據(jù)特性3可推論出紅色節(jié)點必有兩個黑色子節(jié)點(空節(jié)點為黑色)。此時會出現(xiàn)兩種情況:叔節(jié)點為紅色、叔節(jié)點為黑色。
圖例:C 表示當(dāng)前節(jié)點,P 表示父節(jié)點,U 表示叔節(jié)點,G 表示祖父節(jié)點
(1)父節(jié)點與叔節(jié)點都為紅色的情況
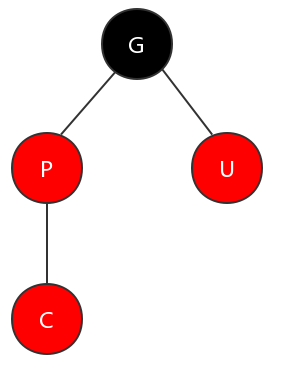
在這種情況下,需要將父節(jié)點和叔節(jié)點變?yōu)楹谏賹⒆娓腹?jié)點變?yōu)榧t色。這樣,圖上所展示的子樹就滿足了紅黑樹的特性。如下圖所示。
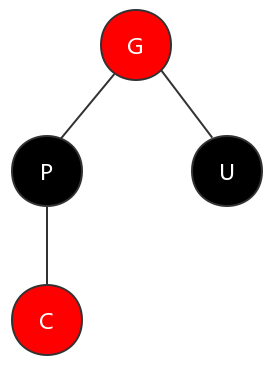
但是這里又可能會產(chǎn)生新的違反特性情況,因為祖父節(jié)點變成了紅色,那么它可能會造成違反特性4的情況。所以,這里就將祖父節(jié)點作為當(dāng)前節(jié)點,進(jìn)行新一輪的調(diào)整操作。
(2)父節(jié)點為紅色,叔節(jié)點為黑色的情況
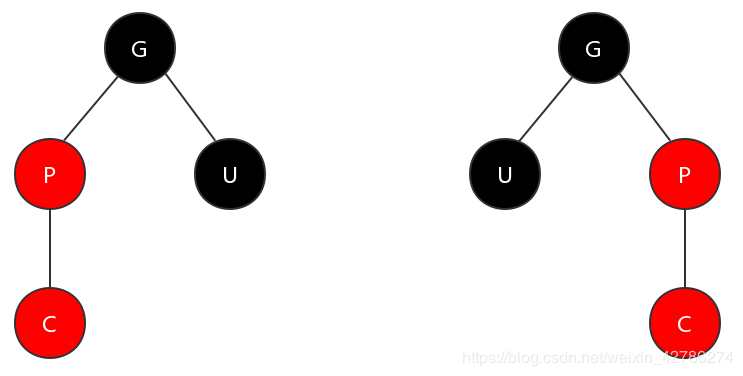
在這種情況下,對其調(diào)整的核心就是保持父節(jié)點分支符合特性4,而叔節(jié)點分支保持符合特性5。
第一步,旋轉(zhuǎn)。對祖父節(jié)點進(jìn)行左旋或者右旋。如果父節(jié)點是祖父節(jié)點的右子節(jié)點,那么對祖父節(jié)點進(jìn)行左旋;否則,對祖父節(jié)點進(jìn)行右旋。 第二步,染色。將祖父節(jié)點染為紅色,而父節(jié)點染為黑色。
進(jìn)過這兩步,上圖的情況會轉(zhuǎn)換為下圖所示。
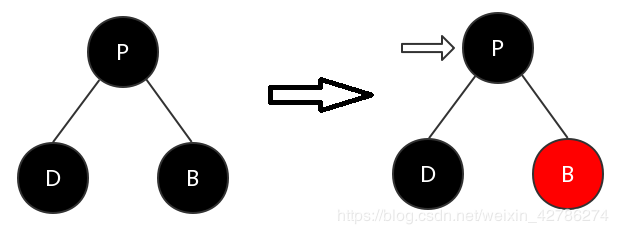
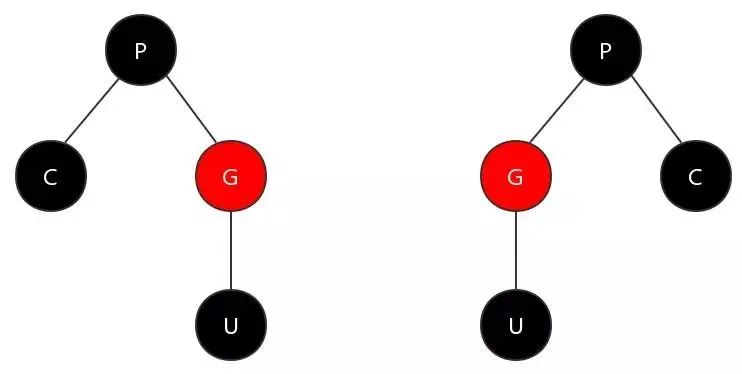
可以看出,父節(jié)點這一分支進(jìn)過調(diào)整后,當(dāng)前節(jié)點與父節(jié)點的顏色不再是連續(xù)紅色,滿足特性4。而叔節(jié)點這一分支的黑色節(jié)點數(shù)目沒有發(fā)生變化,滿足特性5。對原祖父節(jié)點的父節(jié)點來說,該子樹沒有發(fā)生違反特性的變化。該子樹調(diào)整完成。
2.3 檢查根節(jié)點
當(dāng)上述調(diào)整執(zhí)行完后,還有最后一步,就是檢查是否滿足特性2。這一步只需要將根節(jié)點染成黑色就可以,無需再多加判斷。
3. 刪除操作
需要重點理解的就是刪除操作,這個也是我覺得是紅黑樹中最難的部分。
刪除操作要比插入操作略微復(fù)雜一些。因為刪除的節(jié)點可能是出現(xiàn)在樹的中間層的節(jié)點,此時刪除該節(jié)點會遇到很復(fù)雜的情況。所以,在刪除節(jié)點的時候,需要先對紅黑樹進(jìn)行一些調(diào)整,使得刪除節(jié)點對整個樹的影響降到最低。
3.1 替換刪除節(jié)點
首先根據(jù) BST 刪除節(jié)點的規(guī)則,使用當(dāng)前節(jié)點左子樹的最大值節(jié)點或者右子樹的最小值節(jié)點代替其刪除。這兩個節(jié)點是其子樹中數(shù)值上最貼近當(dāng)前節(jié)點數(shù)值的節(jié)點)。這一點,只要懂了二叉查找樹的刪除操作就明白了,在這里不多說了。如下圖所示:
圖例:D 表示當(dāng)前節(jié)點,P 表示父節(jié)點,B 表示兄弟節(jié)點,BR 表示兄弟節(jié)點的右子節(jié)點,BL 表示兄弟節(jié)點的左子節(jié)點
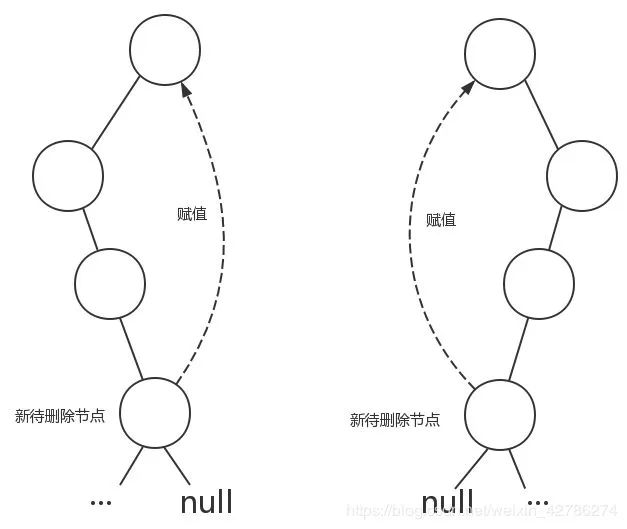
既然待刪除節(jié)點是要被移走的,那肯定有一個節(jié)點要替換到它的位置上去。如何找到這個替換節(jié)點,這個過程和二叉查找樹一模一樣,要么在它的左子樹下一直往右找到最大節(jié)點,要么在右子樹下找到最小節(jié)點。
下面的描述過程采用的是右子樹的最小值節(jié)點代替
當(dāng)找到替換節(jié)點之后,現(xiàn)在需要考慮的情況就減少了,只可能會出現(xiàn)以下幾種情況(因為需要滿足紅黑樹特性):
無子節(jié)點,節(jié)點為紅色 無子節(jié)點,節(jié)點為黑色 只有右子節(jié)點,右子節(jié)點為紅色,節(jié)點本身為黑色
上面這三種情況,說的是新待刪除節(jié)點。新待刪除節(jié)點,就是即將被替換到待刪除位置的節(jié)點。
因為 D 節(jié)點就是即將要替換到待刪節(jié)點位置的節(jié)點,它同時又是右子樹的最小值,既然是最小值了,它就不再可能擁有左子樹了,所以只有可能有右子節(jié)點。另外,假如它有右節(jié)點且右節(jié)點的顏色是黑色,它自身顏色是紅色,根本不成立。因為假如它自身為紅色且又有黑孩子,那它必須要有兩個黑孩子才滿足紅黑樹性質(zhì),所以不滿足。那有沒有可能,它自身是黑色且右孩子也為黑色呢?也不可能!因為它左孩子已經(jīng)為空了,說明它從自身出發(fā)到左子樹的葉子的距離就是1,假如它右孩子也為黑色,那它從自身出發(fā)到右子樹葉子的距離肯定大于等于2了,明顯不可能。
所以總的來說只可能有下面三種情況:
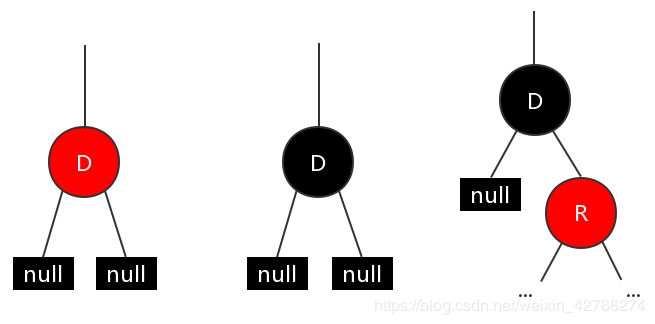
情況1:只需要直接刪除節(jié)點就可以。刪了一個紅色新待刪節(jié)點,不會影響紅黑樹性質(zhì)。 情況2:刪除該 D 節(jié)點后,違反了紅黑樹特性5,需要調(diào)整(不考慮待刪除節(jié)點為根節(jié)點的情況) 情況3:用右子節(jié)點 R 占據(jù)待刪除節(jié)點 D,再將其染成黑色即可,不違反紅黑樹特性。因為左邊本來就是空了,其實右子樹下即使有多少個黑色節(jié)點,也不會影響整體特性。
在這三種情況中,情況1和情況3比較簡單,不需要多余的調(diào)整。情況2則需要后續(xù)的調(diào)整步驟使其滿足紅黑樹特性。
3.2 調(diào)整紅黑樹
上述情況2的調(diào)整比較復(fù)雜。下面對各種情況進(jìn)行講解。
根據(jù)紅黑樹的特性5,待刪除節(jié)點必然有兄弟節(jié)點。
為什么這么說呢?因為我們已經(jīng)假設(shè)上面的 D 節(jié)點不為根了,那說明它肯定有父親。首先它是沒有孩子的,它下面直接就是葉子了,既然有父親,不論它是父親的左孩子或者右孩子,從父親出發(fā)到它自身,黑色節(jié)點的個數(shù)為1。反證法:假如父親只有它一個孩子,那說明父親到另一邊子樹的葉子距離就為0,因為0個節(jié)點。這明顯不符合,所以說明父親肯定有兩個孩子,那從而得知待刪節(jié)點D必有兄弟。
下面根據(jù)其兄弟節(jié)點所在分支的不同,來分情況討論。
以下是以關(guān)注待刪節(jié)點為父節(jié)點的左子節(jié)點進(jìn)行描述,如果遇到關(guān)注節(jié)點為父節(jié)點的右子節(jié)點的情況,則鏡像處理。
**思路:**下面的任何調(diào)整只有一個目的,就是不斷調(diào)整,直到調(diào)整到可以直接將 D 移除又不會影響紅黑樹特性的情況。但關(guān)鍵是調(diào)整過程中紅黑樹特性也不會發(fā)生改變。
圖例:D 表示當(dāng)前節(jié)點,P 表示父節(jié)點,B 表示兄弟節(jié)點,BR 表示兄弟節(jié)點的右子節(jié)點,BL 表示兄弟節(jié)點的左子節(jié)點
(1)兄弟節(jié)點為紅色

將父節(jié)點染成紅色,兄弟節(jié)點染成黑色,然后對父節(jié)點進(jìn)行左旋操作。此時就轉(zhuǎn)換為了下面的(4),之后按照(4)繼續(xù)進(jìn)行調(diào)整。
分析:這種情況,樹的整體高度為2,變色左旋之后,整體高度還是保持在2。
(2)兄弟節(jié)點為黑色,遠(yuǎn)侄節(jié)點為紅色
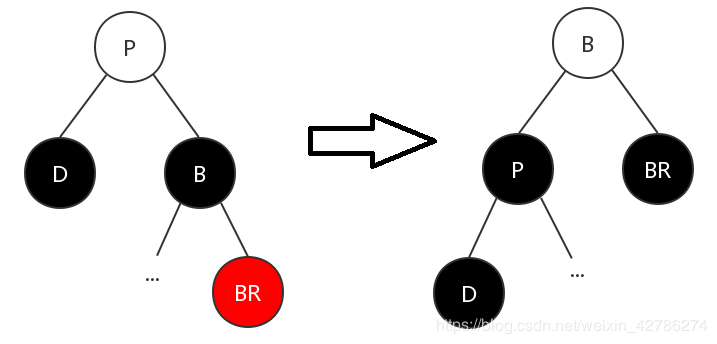
這種情況下,不需要考慮父節(jié)點的顏色。
將父節(jié)點 P 與兄弟節(jié)點 B 的顏色互換 ,這個過程父親染黑 將兄弟節(jié)點的右子節(jié)點 BR 染成黑色 對父節(jié)點 P 進(jìn)行左旋操作
可以看到,原本高度就是符合紅黑樹特性的,左右子樹的高度都為1,因為黑色節(jié)點只有一個。經(jīng)過這三步的調(diào)整后,直接刪除節(jié)點 D 后仍然滿足紅黑樹的特性,調(diào)整完成,跳出算法循環(huán)。
(3)兄弟節(jié)點為黑色,遠(yuǎn)侄節(jié)點為黑色,近侄節(jié)點為紅色
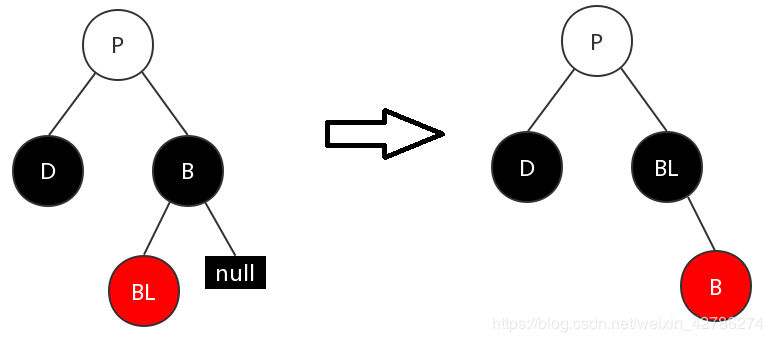
這種情況下,兄弟節(jié)點的左節(jié)點染成黑色。兄弟節(jié)點染紅。然后對兄弟節(jié)點做右旋。此時的狀況就和(2)一樣了。之后就通過(2)的調(diào)整方式進(jìn)行調(diào)整。
(4)父節(jié)點為紅色,兄弟節(jié)點為黑色,兄弟節(jié)點無子節(jié)點
這種情況下,將父節(jié)點P染成黑色,再將兄弟節(jié)點染成紅色。經(jīng)過這樣的操作后,除去節(jié)點D后,以P為根節(jié)點的子樹的黑節(jié)點深度并沒有發(fā)生變化。調(diào)整完成。
怎么理解這個操作?
可以看左邊,沒調(diào)整前,P 的左右子樹的黑色結(jié)點的數(shù)目都是1,是相同的,符合紅黑樹的性質(zhì):從任一節(jié)點到其葉子的所有簡單路徑都包含相同數(shù)目的黑色節(jié)點。然后再看右邊,調(diào)整后,刪掉 D 之后,P 結(jié)點的左右子樹的黑色結(jié)點都是0個,仍然滿足性質(zhì),所以調(diào)整完成。
(5)父節(jié)點為黑色,兄弟節(jié)點為黑色,兄弟節(jié)點無子節(jié)點

這種情況下,為了在刪除節(jié)點 D 后使以 P 為根節(jié)點的子樹能滿足紅黑樹特性5,將兄弟節(jié)點 B 染成紅色。但是這樣操作后,以 P 為根節(jié)點的子樹的黑色節(jié)點深度變小了。所以需要繼續(xù)調(diào)整。
因為P節(jié)點子樹的黑色深度發(fā)生了減少,可以把其當(dāng)作待刪除節(jié)點,那么此時就以 P 節(jié)點為關(guān)注節(jié)點進(jìn)行進(jìn)一步調(diào)整(繼續(xù)向上調(diào)整)。這句話的意思我們再以 P 為起始點,繼續(xù)根據(jù)情況進(jìn)行平衡操作。就是把 P 當(dāng)成 D,只是不要再刪除 P 了。再看是這五種中的哪種情況,再進(jìn)行對應(yīng)的調(diào)整,這樣一直向上,直到新的起始點為根節(jié)點或者關(guān)注節(jié)點不為黑色。
第五種情況,不會一直連續(xù)回溯的。假如能一直回溯,指針向上走之后,兄弟節(jié)點會一直都沒有右孩子嗎?不存在的。假如有這種情況,說明樹的路徑長度已經(jīng)嚴(yán)重往左傾斜,肯定不可能。所以回溯這個情況只會回溯一次,不會連續(xù)回溯。第五個這種情況出現(xiàn)之后,下一次進(jìn)入算法循環(huán),肯定就是進(jìn)入其他情況,直到遇到 break,跳出循環(huán),終止整個算法過程。
3.3 檢查根節(jié)點及刪除節(jié)點
經(jīng)過上述的調(diào)整后,此時基本滿足了紅黑樹的特性。但是存在根節(jié)點變成紅色的情況。所以需要將根節(jié)點染成黑色的操作。最后,執(zhí)行刪除操作,將待刪除節(jié)點刪掉。
當(dāng)然從編程的角度,你也可以調(diào)整指針先把待刪除節(jié)點移掉,然后再開始平衡調(diào)整過程。注意這里說的平衡調(diào)整,并不是 AVL 樹的絕對平衡調(diào)整,而是滿足紅黑樹特性的平衡調(diào)整。紅黑樹的平衡和 AVL 的平衡是有區(qū)別的。
Java實現(xiàn)
上面的操作篇幅比較長,假如沒看明白,可以通過下面的代碼繼續(xù)看。
由于篇幅限制,源碼請到原文鏈接查看 Java 實現(xiàn)
blog.csdn.net/weixin_42786274/article/details/86557922
總結(jié)
紅黑樹的刪除操作是整個紅黑樹中最復(fù)雜的一部分,理解了這部分,紅黑樹就算基本拿下了。理解完一種數(shù)據(jù)結(jié)構(gòu),要能 get 到作者當(dāng)初設(shè)計時的點,才算是一次積累。紅黑樹的刪除操作,它非常地巧妙,整一個算法循環(huán)過程,它不會超過三次,調(diào)整過程基本都在子樹內(nèi)完成,指針不需要一直向上回溯,相比 AVL 樹,AVL 樹在刪除節(jié)點時,指針有可能會一直回溯到根為止。
來源:xyk_1021
blog.csdn.net/weixin_42786274/article/details/86557922
推薦閱讀:
不是你需要中臺,而是一名合格的架構(gòu)師(附各大廠中臺建設(shè)PPT)
企業(yè)IT技術(shù)架構(gòu)規(guī)劃方案
論數(shù)字化轉(zhuǎn)型——轉(zhuǎn)什么,如何轉(zhuǎn)?
企業(yè)10大管理流程圖,數(shù)字化轉(zhuǎn)型從業(yè)者必備!
【中臺實踐】華為大數(shù)據(jù)中臺架構(gòu)分享.pdf
超詳細(xì)280頁Docker實戰(zhàn)文檔!開放下載
