硬核圖解紅黑樹并手寫實(shí)現(xiàn)
“程序員常用的IDEA插件:https://github.com/silently9527/ToolsetIdeaPlugin
微信公眾號(hào):貝塔學(xué)Java
”
前言
在上一篇中我們通過二叉樹作為了Map的實(shí)現(xiàn),最后也分析了該版本的時(shí)間復(fù)雜度以及最糟糕的情況;本篇我們將會(huì)使用紅黑樹來實(shí)現(xiàn)Map,改善上一篇中二叉樹版本的不足;對(duì)于Map接口的定義以及已經(jīng)實(shí)現(xiàn)的公用方法將不會(huì)重復(fù)敘述,比如二叉樹的查找方法(get);不了解的兄弟請(qǐng)查看上一篇《基于二叉樹實(shí)現(xiàn)Map》
紅黑樹算是數(shù)據(jù)結(jié)構(gòu)中比較有難度的知識(shí)點(diǎn),雖然在實(shí)際的業(yè)務(wù)開發(fā)工作中使用的不多,但是這是面試官最喜歡問的知識(shí)點(diǎn)。
我在之前也看過很多關(guān)于紅黑樹的文章,但是很多都是從紅黑樹的性質(zhì)來講紅黑樹,根本未從紅黑樹的理論模型出發(fā)講紅黑樹,所以造成紅黑樹比較難理解。
理解并掌握紅黑樹還是有必要的,Java中的HashMap當(dāng)鏈表的節(jié)點(diǎn)數(shù)超過了8個(gè)就會(huì)把鏈表轉(zhuǎn)換成紅黑樹;TreeMap底層也是用的是紅黑樹;
紅黑樹于我們上一篇討論的二叉樹相比,紅黑樹幾乎是完美平衡的,并且能夠保證操作的運(yùn)行時(shí)間都是對(duì)數(shù)級(jí)別
在學(xué)習(xí)紅黑樹之前,我們先來看看紅黑樹的性質(zhì),針對(duì)每一條性質(zhì)我們都需要問一個(gè)Why,帶著問題去學(xué)習(xí)紅黑樹;如果我們搞懂了這些問題,那么就理解了紅黑樹本質(zhì),當(dāng)然與實(shí)現(xiàn)還有一些距離。
性質(zhì)1. 結(jié)點(diǎn)是紅色或黑色。(why:為什么節(jié)點(diǎn)要區(qū)分顏色,紅色節(jié)點(diǎn)的作用是什么?) 性質(zhì)2. 根結(jié)點(diǎn)是黑色。(why:為什么根節(jié)點(diǎn)必須是黑色) 性質(zhì)3. 所有葉子都是黑色。(why) 性質(zhì)4. 從每個(gè)葉子到根的所有路徑上不能有兩個(gè)連續(xù)的紅色結(jié)點(diǎn)。(why) 性質(zhì)5. 從任一節(jié)結(jié)點(diǎn)其每個(gè)葉子的所有路徑都包含相同數(shù)目的黑色結(jié)點(diǎn)。(why) 性質(zhì)6. 每次新插入的節(jié)點(diǎn)都必須是紅色(why)
平衡查找樹
紅黑樹是近似平衡的二叉樹,紅黑樹對(duì)應(yīng)的理論模型可以是2-3樹,也可以是2-3-4樹,所以在學(xué)習(xí)紅黑樹之前,我們需要先了解2-3樹和2-3-4樹;
紅黑樹與2-3樹、2-3-4樹的關(guān)系就好比接口與實(shí)現(xiàn)類的關(guān)系;2-3樹與2-3-4樹是接口,而紅黑樹是基于接口的實(shí)現(xiàn)
2-3樹、2-3-4樹都是B樹的特列情況
2-3樹
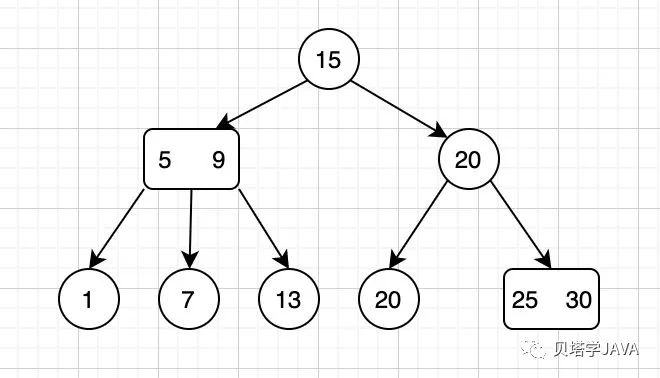
為了保證樹的絕對(duì)平衡,允許樹中的節(jié)點(diǎn)保存多個(gè)鍵值,在2-3樹中可以出現(xiàn)一個(gè)節(jié)點(diǎn)存在一個(gè)鍵值兩條鏈接,也允許同一個(gè)節(jié)點(diǎn)包含最多兩個(gè)鍵三條鏈接;
2-3樹如下圖:
查找
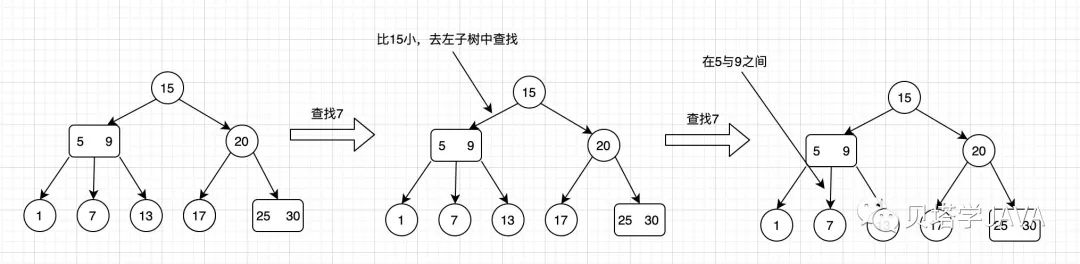
2-3樹的查找過程與二叉樹類似,查找鍵與節(jié)點(diǎn)中的鍵比較,如果遇到與查找鍵相等的節(jié)點(diǎn),查找命中;否則繼續(xù)去對(duì)應(yīng)的子樹中去查找,如果遇到空的鏈接表示查找未命中。
插入
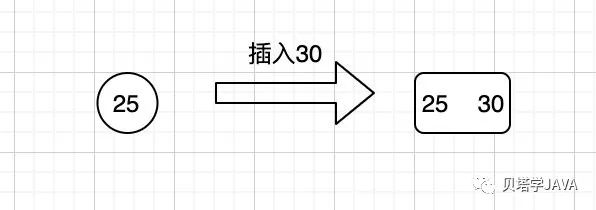
向單鍵key的節(jié)點(diǎn)中插入:當(dāng)前節(jié)點(diǎn)只有一個(gè)key, 直接在當(dāng)前節(jié)點(diǎn)新增一個(gè)key
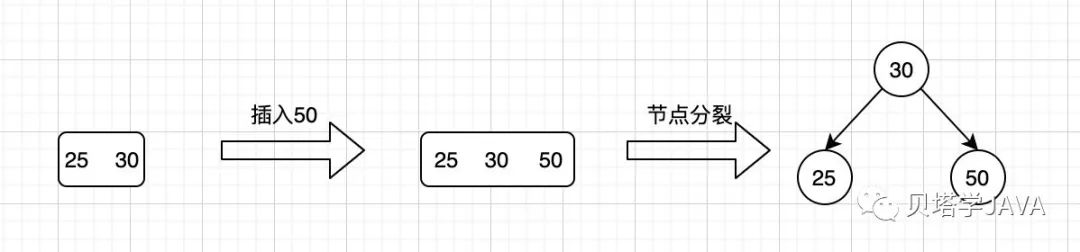
向雙鍵key的節(jié)點(diǎn)中插入:先插入新的key到當(dāng)前節(jié)點(diǎn),如果當(dāng)前節(jié)點(diǎn)大于了兩個(gè)key
向雙鍵key的節(jié)點(diǎn)中插入,并且父節(jié)點(diǎn)也是雙鍵
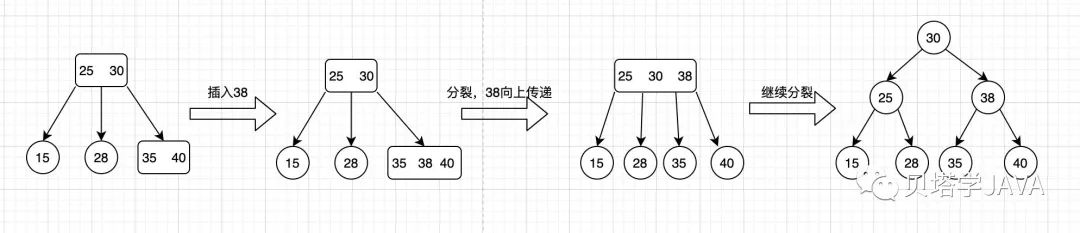
通過上面的三種情況的演示,我們發(fā)現(xiàn)2-3樹和標(biāo)準(zhǔn)的二叉樹的生長是不同的,二叉樹的生長是由上向下生長的,而2-3樹的生長是由下向上的。
在上一篇的二叉樹中,我們發(fā)現(xiàn)最糟糕的情況是插入的節(jié)點(diǎn)有序,導(dǎo)致二叉樹退化成了鏈表,性能下降,我們使用2-3樹順序插入看看如何,例如順序插入1,2,3,4,5,6,7
由此我們可以看出在最壞的情況下2-3樹依然完美平衡的,有比較好的性能。但是這是理論,與真正的實(shí)現(xiàn)還是有一段距離
基于2-3樹實(shí)現(xiàn)的左傾紅黑樹
了解了紅黑樹的理論模型2-3樹之后,那么就可以基于2-3樹來實(shí)現(xiàn)我們的紅黑樹。
由于2-3樹中存在著雙鍵的節(jié)點(diǎn),由于我們需要在二叉樹中表示出雙鍵的節(jié)點(diǎn),所以我們需要在節(jié)點(diǎn)中添加一個(gè)顏色的屬性color,如果節(jié)點(diǎn)是紅色,那么表示當(dāng)前節(jié)點(diǎn)和父節(jié)點(diǎn)共同組成了2-3樹中的雙鍵節(jié)點(diǎn)。
對(duì)上一篇中二叉樹的節(jié)點(diǎn)做一些修改,代碼如下:
class Node implements TreeNode {
public static final boolean RED = true;
public static final boolean BLACK = false;
public K key;
public V value;
public Node left;
public Node right;
public boolean color; //RED 或者 BLACK
public int size = 1; //當(dāng)前節(jié)點(diǎn)下節(jié)點(diǎn)的總個(gè)數(shù)
public Node(K key, V value, boolean color) {
this.key = key;
this.value = value;
this.color = color;
}
@Override
public Node getLeft() {
return this.left;
}
@Override
public Node getRight() {
return this.right;
}
@Override
public Color getColor() {
return color ? Color.RED : Color.BLACK;
}
}
由于紅黑樹本身也是二叉樹,所以在上一篇中實(shí)現(xiàn)的二叉樹查找方法可以不用做任何的修改就可以直接應(yīng)用到紅黑樹。
本篇中我們實(shí)現(xiàn)的2-3樹紅黑樹參考算法4,并且我們規(guī)定紅色節(jié)點(diǎn)只能出現(xiàn)在左節(jié)點(diǎn),即左傾紅黑樹。(為什么規(guī)定紅色節(jié)點(diǎn)只能出現(xiàn)在左節(jié)點(diǎn)?其實(shí)右邊也是可以的,只允許存在左節(jié)點(diǎn)是因?yàn)槟軌驕p少可能出現(xiàn)的情況,實(shí)現(xiàn)所需的代碼相對(duì)較小)
紅黑樹性質(zhì)解釋
紅黑樹作為了2-3樹的實(shí)現(xiàn),基于2-3樹去看紅黑樹的性質(zhì)就不在是干癟癟的約定,也不需要要強(qiáng)行記憶。
性質(zhì)1. 結(jié)點(diǎn)是紅色或黑色。(why:為什么節(jié)點(diǎn)要區(qū)分顏色,紅色節(jié)點(diǎn)的作用是什么?) 在上面我們已經(jīng)解釋過了,要區(qū)分顏色主要是想要在二叉樹中來表示出2-3樹的雙鍵節(jié)點(diǎn)的情況,如果是紅色節(jié)點(diǎn),那么表示當(dāng)前節(jié)點(diǎn)與父節(jié)點(diǎn)共同組成了2-3數(shù)的雙鍵;黑色節(jié)點(diǎn)表示二叉樹中的普通節(jié)點(diǎn)
性質(zhì)2. 根結(jié)點(diǎn)是黑色。(why:為什么根節(jié)點(diǎn)必須是黑色) 還是基于紅色節(jié)點(diǎn)的作用來理解,根節(jié)點(diǎn)本身沒有父節(jié)點(diǎn),無法組成2-3樹雙鍵,所以不可能是紅色節(jié)點(diǎn)。
性質(zhì)3. 所有葉子都是黑色。(why) 此處提到的葉子其實(shí)是空鏈接,在上面的圖中空連接未畫出。
性質(zhì)4. 從每個(gè)葉子到根的所有路徑上不能有兩個(gè)連續(xù)的紅色結(jié)點(diǎn)。(why) 此性質(zhì)還是基于紅色節(jié)點(diǎn)的作用來理解,如果出現(xiàn)了兩個(gè)連續(xù)的紅色節(jié)點(diǎn),那么與父節(jié)點(diǎn)組成了3鍵的節(jié)點(diǎn),但是這在2-3樹實(shí)現(xiàn)的左傾紅黑樹中是不允許的。(在基于2-3-4樹實(shí)現(xiàn)的紅黑樹中允許出現(xiàn)3鍵,但是只能是左右兩邊各一個(gè)紅色節(jié)點(diǎn),也不能連續(xù),在后面擴(kuò)展部分會(huì)有講解)
性質(zhì)5. 從任一節(jié)結(jié)點(diǎn)到其每個(gè)葉子的所有路徑都包含相同數(shù)目的黑色結(jié)點(diǎn)。(why) 此性質(zhì)可以基于2-3樹的理論模型來理解,因?yàn)樵诩t色節(jié)點(diǎn)表示與父節(jié)點(diǎn)同層高,所以在紅黑樹中只有黑色節(jié)點(diǎn)會(huì)貢獻(xiàn)樹的高度,所以從任一節(jié)結(jié)點(diǎn)到其每個(gè)葉子的所有路徑都包含相同數(shù)目的黑色結(jié)點(diǎn)
性質(zhì)6. 每次新插入的節(jié)點(diǎn)都必須是紅色(why) 此性質(zhì)在百度百科中未出現(xiàn),但在一些國外網(wǎng)站上有看到,個(gè)人覺得對(duì)于理解紅黑樹也有幫助,所以加在了這里;在上面我們已經(jīng)演示過了2-3樹插入鍵的過程,先插入鍵值到節(jié)點(diǎn),然后在判斷是否需要分裂,因?yàn)閮?yōu)先插入建到當(dāng)前節(jié)點(diǎn)組成2-3樹的雙鍵或3鍵,而在紅黑樹中只有通過使用紅色節(jié)點(diǎn)與父節(jié)點(diǎn)組成2-3樹的雙鍵或3鍵,所以每次新插入的節(jié)點(diǎn)都必須是紅色。
2-3樹在左傾紅黑樹中表示
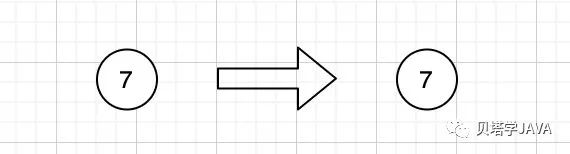
2-3樹中單鍵節(jié)點(diǎn)在紅黑樹中的表示
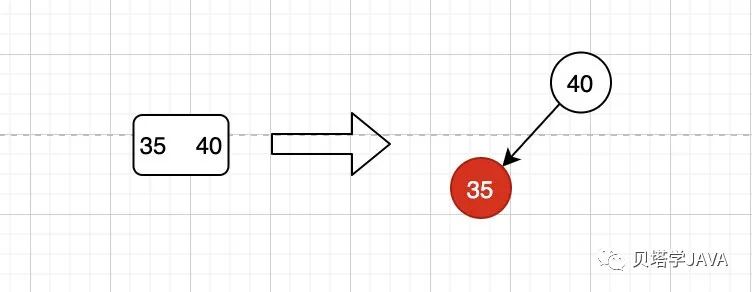
2-3樹中雙鍵節(jié)點(diǎn)在紅黑樹中的表示,由于是左傾紅黑樹,所以只能出現(xiàn)紅色節(jié)點(diǎn)在左邊
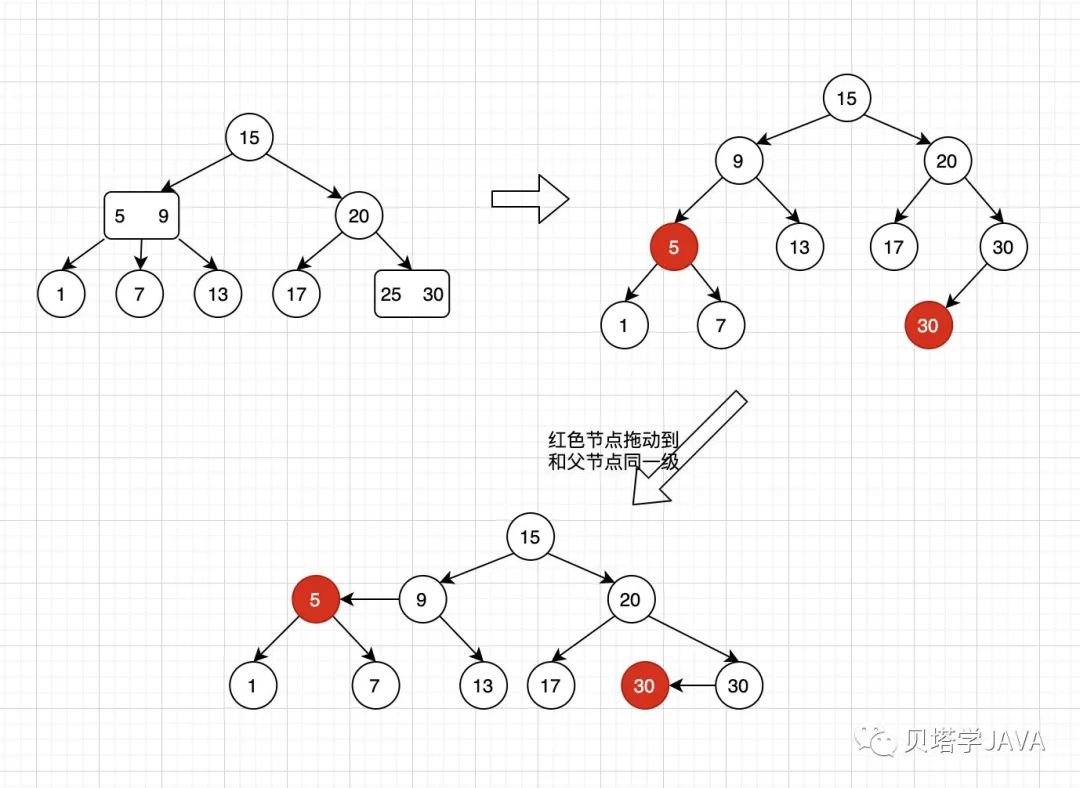
只看節(jié)點(diǎn)的變化可能不太直觀,我們可以來看一個(gè)2-3樹如何表示成左傾紅黑樹
當(dāng)我們把紅色節(jié)點(diǎn)拖動(dòng)到與父節(jié)點(diǎn)同一個(gè)高度的時(shí)候,可以與2-3樹對(duì)比來看,發(fā)現(xiàn)紅黑樹很好的表示了2-3樹
判斷節(jié)點(diǎn)的顏色
我需要定義個(gè)方法來判斷節(jié)點(diǎn)屬于什么顏色,如果是紅色就返回true,否則返回false
protected boolean isRed(Node node) {
if (Objects.isNull(node)) {
return Node.BLACK;
}
return node.color;
}
旋轉(zhuǎn)
在實(shí)現(xiàn)紅黑樹的插入或者刪除操作可能會(huì)出現(xiàn)紅色節(jié)點(diǎn)在右邊或者兩個(gè)連續(xù)的紅色節(jié)點(diǎn),在出現(xiàn)這些情況的時(shí)候我們需要通過旋轉(zhuǎn)操作來完成修復(fù)。
由于旋轉(zhuǎn)操作完成之后需要修改父節(jié)點(diǎn)的鏈接,所以我們定義的旋轉(zhuǎn)方法需要返回旋轉(zhuǎn)之后的節(jié)點(diǎn)來重置父節(jié)點(diǎn)的鏈接
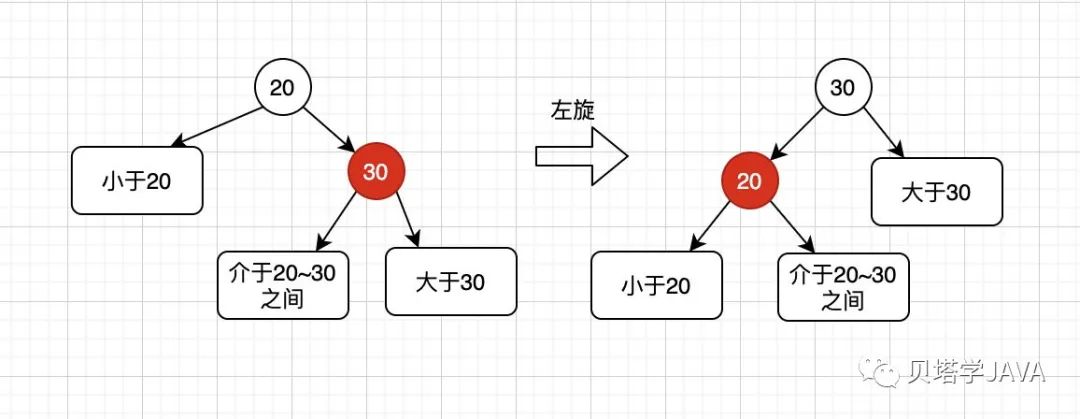
左旋
左旋代碼實(shí)現(xiàn)如下:
protected Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = Node.RED;
size(h); //計(jì)算子樹節(jié)點(diǎn)的個(gè)數(shù)
size(x);
return x;
}
重新指定兩個(gè)節(jié)點(diǎn)的左右子樹的鏈接,并且修改節(jié)點(diǎn)的顏色。其次是計(jì)算每個(gè)子樹所包含的節(jié)點(diǎn)個(gè)數(shù),計(jì)算的方式與上一篇中二叉樹的size實(shí)現(xiàn)類似,這里就不重復(fù)敘述,參考《基于二叉樹實(shí)現(xiàn)Map》
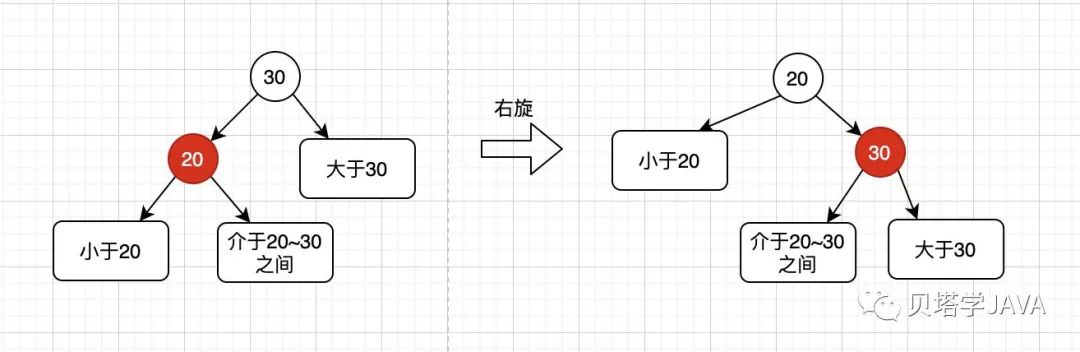
右旋
右旋代碼實(shí)現(xiàn)如下:
protected Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = Node.RED;
size(h);
size(x);
return x;
}
變色
在2-3樹中,當(dāng)節(jié)點(diǎn)中的key值達(dá)到了3個(gè)就需要進(jìn)行分裂,其中一個(gè)節(jié)點(diǎn)將會(huì)上浮;那在紅黑樹中應(yīng)該如何來表示這個(gè)操作呢?
在紅黑樹中要實(shí)現(xiàn)節(jié)點(diǎn)分裂,其實(shí)就是節(jié)點(diǎn)顏色的變化;紅黑樹經(jīng)過左旋右旋之后最終都會(huì)達(dá)到父節(jié)點(diǎn)是黑色,左右兩個(gè)子節(jié)點(diǎn)是紅色(后面再插入操作中可以看到詳細(xì)的轉(zhuǎn)變過程),這種狀態(tài)就對(duì)應(yīng)了2-3樹中的三鍵節(jié)點(diǎn)的情況,這時(shí)候分裂的操作就是把左右兩個(gè)子節(jié)點(diǎn)的顏色變成黑色,父節(jié)點(diǎn)變成紅色。
代碼實(shí)現(xiàn)如下:
/轉(zhuǎn)換顏色,對(duì)應(yīng)了23樹中的節(jié)點(diǎn)分裂
protected void upSplit(Node node) {
if (Objects.isNull(node)) {
return;
}
node.left.color = Node.BLACK;
node.right.color = Node.BLACK;
node.color = Node.RED;
}
插入
向單鍵節(jié)點(diǎn)插入
如果插入的鍵小于當(dāng)前節(jié)點(diǎn)的鍵值,那么直接新增一個(gè)紅色左節(jié)點(diǎn)
如果插入的鍵大于當(dāng)前節(jié)點(diǎn)的鍵值,那么插入一個(gè)紅色的右節(jié)點(diǎn),由于只允許左邊出現(xiàn)紅色節(jié)點(diǎn),所以我們需要進(jìn)行左旋一次
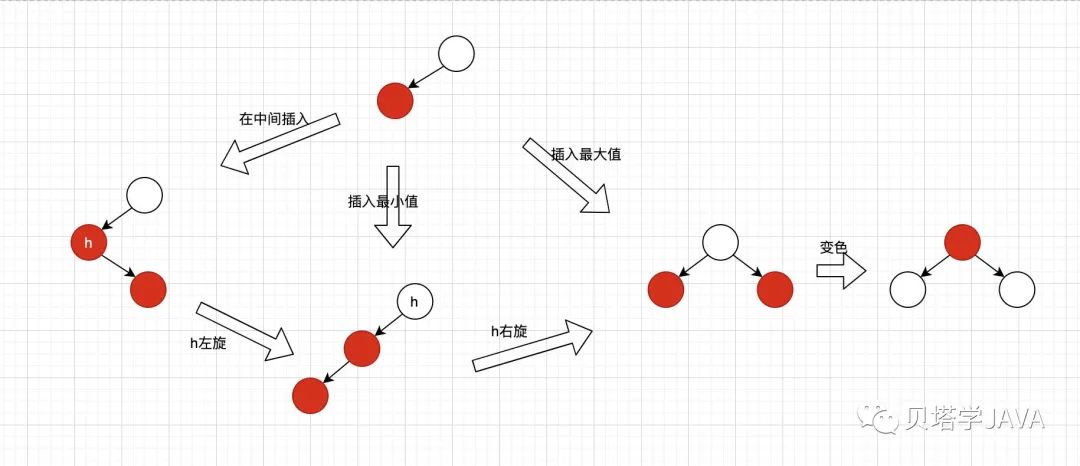
向雙鍵節(jié)點(diǎn)中插入
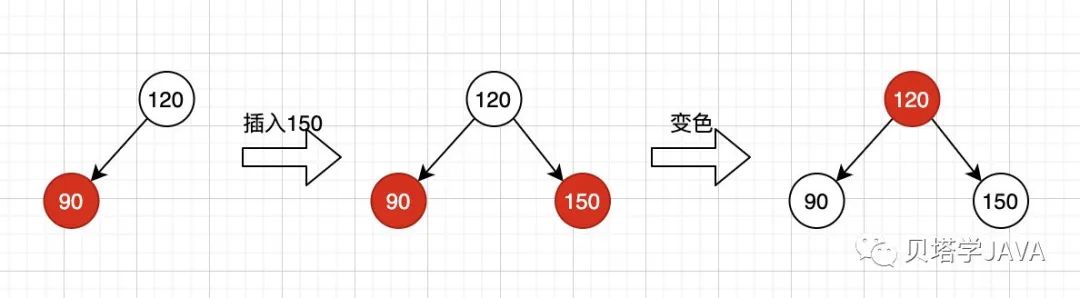
向雙鍵節(jié)點(diǎn)中插入新的鍵有三種情況,我們先來看最簡單的情況,插入的鍵值最大,插入之后只需要變化顏色即可,變化過程如下圖
第二種情況是插入的鍵值最小,插入之后造成了兩個(gè)紅色節(jié)點(diǎn)相連,所以需要進(jìn)行右旋,然后在變色
第三種情況插入的鍵值在原來兩鍵之間,需要先進(jìn)行左旋,再右旋,最后在變色
根據(jù)以上各種情況的分析,我們可以總結(jié)出統(tǒng)一的變化規(guī)律:
若右子節(jié)點(diǎn)是紅色,左子節(jié)點(diǎn)是黑樹,那么就進(jìn)行左旋 若左子節(jié)點(diǎn)是紅色且他的左子節(jié)點(diǎn)也是紅色,那么就進(jìn)行右旋 若左右子節(jié)點(diǎn)都是紅色,那么就進(jìn)行顏色轉(zhuǎn)換
圖形變化如下:
經(jīng)過上面的分析之后我們現(xiàn)在可以來代碼實(shí)現(xiàn)紅黑樹的插入操作
@Override
public void put(K key, V value) {
if (Objects.isNull(key)) {
throw new IllegalArgumentException("the key can't null");
}
root = put(root, key, value);
root.color = Node.BLACK;
}
private Node put(Node node, K key, V value) {
if (Objects.isNull(node)) {
return new Node(key, value, Node.RED);
}
int compare = key.compareTo(node.key);
if (compare > 0) {
node.right = put(node.right, key, value);
} else if (compare < 0) {
node.left = put(node.left, key, value);
} else {
node.value = value;
}
if (isRed(node.right) && !isRed(node.left)) {
node = rotateLeft(node);
}
if (isRed(node.left) && isRed(node.left.left)) {
node = rotateRight(node);
}
if (isRed(node.left) && isRed(node.right)) {
upSplit(node);
}
size(node);
return node;
}
由于根節(jié)點(diǎn)必須為黑色的性質(zhì),防止變色操作把根節(jié)點(diǎn)變?yōu)榧t色,所以我們?cè)诓迦氩僮髦蠼y(tǒng)一設(shè)置一次根節(jié)點(diǎn)為黑色;
紅黑樹的插入操作前半部分和上一篇實(shí)現(xiàn)的二叉樹的插入操作一致,唯一不同的只有最后三個(gè)if操作,這三個(gè)操作就是上面總結(jié)的統(tǒng)一變化規(guī)律的代碼實(shí)現(xiàn)。
第一個(gè)if判斷處理如果右節(jié)點(diǎn)是紅色,左節(jié)點(diǎn)是黑色,那么就進(jìn)行左旋
第二個(gè)if判斷處理如果左節(jié)點(diǎn)時(shí)紅色且他的左節(jié)點(diǎn)也是紅色,那么就進(jìn)行右旋
第三個(gè)if判斷如果左右兩個(gè)子節(jié)點(diǎn)都是紅色,那么就進(jìn)行變色
刪除
因?yàn)閯h除操作可能會(huì)造成樹不平衡,并且可能會(huì)破壞紅黑樹的性質(zhì),所以刪除操作會(huì)比插入操作更加麻煩。
首先我們需要先回到2-3樹的理論模型中,如果我們刪除的節(jié)點(diǎn)當(dāng)前是雙鍵節(jié)點(diǎn),那么我們可以直接進(jìn)行刪除操作,樹的高度也不會(huì)結(jié)構(gòu)也不會(huì)發(fā)生變化;所以紅黑樹的刪除操作的關(guān)鍵就是需要保證待刪除節(jié)點(diǎn)是一個(gè)雙鍵的節(jié)點(diǎn)。
在執(zhí)行刪除操作時(shí)我們也會(huì)實(shí)現(xiàn)到變色的操作,這里的變色和插入是的變色操作恰好相反,父節(jié)點(diǎn)變?yōu)楹谏瑑蓚€(gè)子節(jié)點(diǎn)變?yōu)榧t色
protected void flipColors(Node h) {
h.color = !h.color;
h.left.color = !h.left.color;
h.right.color = !h.right.color;
}
在正式實(shí)現(xiàn)刪除操作之前,我們先來討論下紅黑樹刪除最小值和最大值的情況,最后實(shí)現(xiàn)的刪除操作也會(huì)使用到刪除最小值和刪除最大值
刪除最小值
二叉樹刪除最小值就是一直沿著樹的左子樹中查找,直到遇到一個(gè)節(jié)點(diǎn)的左子樹為null,那么就刪除該節(jié)點(diǎn)
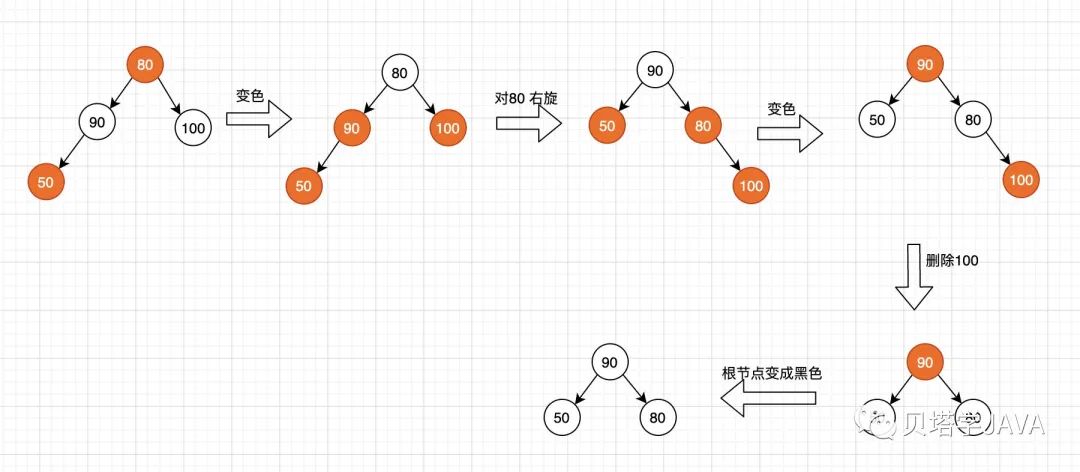
紅黑樹的刪除最小值類似,但是我們需要保證待刪除的節(jié)點(diǎn)是一個(gè)雙鍵的節(jié)點(diǎn),所以在在遞歸到每個(gè)節(jié)點(diǎn)是都需要保住當(dāng)前節(jié)點(diǎn)是雙鍵節(jié)點(diǎn),那么在最后找到的最小值就一定會(huì)在一個(gè)雙鍵節(jié)點(diǎn)中(因?yàn)檫f歸時(shí)已經(jīng)保住的父節(jié)點(diǎn)是雙鍵節(jié)點(diǎn))。
那么如果保證當(dāng)前遞歸節(jié)點(diǎn)是一個(gè)雙鍵節(jié)點(diǎn)呢?這里就會(huì)有3中情況:
當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)是一個(gè)雙鍵節(jié)點(diǎn),直接刪除
當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)是一個(gè)單鍵節(jié)點(diǎn),但他的兄弟是一個(gè)雙鍵節(jié)點(diǎn),那么通過旋轉(zhuǎn)移動(dòng)一個(gè)節(jié)點(diǎn)到左子節(jié)點(diǎn)形成雙鍵節(jié)點(diǎn)之后,再執(zhí)行刪除操作
當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)和右子節(jié)點(diǎn)都是單鍵節(jié)點(diǎn),那么通過變色與父節(jié)點(diǎn)共同形成三鍵節(jié)點(diǎn)之后,再執(zhí)行刪除
以上是紅黑樹刪除最小值會(huì)遇到的所有情況,針對(duì)最后兩種情況,為了代碼的實(shí)現(xiàn)簡單,我們考慮把這兩種情況進(jìn)行合并;
先把初始化根節(jié)點(diǎn)為紅色,再進(jìn)行變色,然后判斷是否node.right.left是紅色,如果是就進(jìn)行旋轉(zhuǎn)操作
刪除最小值的代碼實(shí)現(xiàn)如下:
private Node moveToRedLeft(Node h) {
flipColors(h);
if (isRed(h.right.left)) {
h.right = rotateRight(h.right);
h = rotateLeft(h);
flipColors(h);
}
return h;
}
@Override
public void deleteMin() {
if (isEmpty()) {
throw new NoSuchElementException("BST underflow");
}
if (!isRed(root.left) && !isRed(root.right)) {
root.color = Node.RED;
}
root = deleteMin(root);
if (!isEmpty()) {
root.color = Node.BLACK;
}
}
private Node deleteMin(Node h) {
if (h.left == null) {
return null;
}
if (!isRed(h.left) && !isRed(h.left.left)) {
h = moveToRedLeft(h);
}
h.left = deleteMin(h.left);
return balance(h);
}
private Node balance(Node h) {
if (isRed(h.right) && !isRed(h.left)) {
h = rotateLeft(h);
}
if (isRed(h.left) && isRed(h.left.left)) {
h = rotateRight(h);
}
if (isRed(h.left) && isRed(h.right)) {
flipColors(h);
}
h.size = size(h.left) + size(h.right) + 1;
return h;
}
在刪除掉最小值之后,我們需要重新修復(fù)紅黑樹,因?yàn)橹拔覀兊牟僮骺赡軙?huì)導(dǎo)致3鍵節(jié)點(diǎn)的存在,刪除之后我們需要重新分解3建節(jié)點(diǎn);上面代碼中的balance就是重新修復(fù)紅黑樹。
刪除最大值
刪除最大值思路和刪除最小值的思路類似,這里就不詳細(xì)敘述了,直接上圖
刪除最大值需要從左節(jié)點(diǎn)中借一個(gè)節(jié)點(diǎn),代碼實(shí)現(xiàn)如下:
@Override
public void deleteMax() {
if (isEmpty()) {
throw new NoSuchElementException("BST underflow");
}
if (!isRed(root.left) && !isRed(root.right)) {
root.color = Node.RED;
}
root = deleteMax(root);
if (!isEmpty()) {
root.color = Node.BLACK;
}
}
private Node deleteMax(Node node) {
if (isRed(node.left)) { //此處與刪除最小值不同,如果左邊是紅色,那么先借一個(gè)節(jié)點(diǎn)到右邊來
node = rotateRight(node);
}
if (Objects.isNull(node.right)) {
return null;
}
if (!isRed(node.right) && !isRed(node.right.left)) {
node = moveToRedRight(node);
}
node.right = deleteMax(node.right);
return balance(node);
}
private Node moveToRedRight(Node node) {
flipColors(node);
if (isRed(node.left.left)) {
node = rotateRight(node);
flipColors(node);
}
return node;
}
刪除任意節(jié)點(diǎn)
在查找路徑上進(jìn)行和刪除最小值相同的變換可以保證在查找過程中任意當(dāng)前節(jié)點(diǎn)不會(huì)是雙鍵節(jié)點(diǎn);
如果查找的鍵值在左節(jié)點(diǎn),那么就執(zhí)行與刪除最小值類似的變化,從右邊借節(jié)點(diǎn);
如果查找的鍵值在右節(jié)點(diǎn),那么就執(zhí)行與刪除最大值類似的變化,從左邊借節(jié)點(diǎn)。
如果待刪除的節(jié)點(diǎn)處理葉子節(jié)點(diǎn),那么可以直接刪除;如果是非葉子節(jié)點(diǎn),那么左子樹不為空就與左子樹中最大值進(jìn)行交換,然后刪除左子樹中的最大值,左子樹為空就與右子樹最小值進(jìn)行交換,然后刪除右子樹中的最小值。
代碼實(shí)現(xiàn)如下:
@Override
public void delete(K key) {
if (isEmpty()) {
throw new NoSuchElementException("BST underflow");
}
if (!isRed(root.left) && !isRed(root.right)) {
root.color = Node.RED;
}
root = delete(root, key);
if (!isEmpty()) {
root.color = Node.BLACK;
}
}
private Node delete(Node node, K key) {
int compare = key.compareTo(node.key);
if (compare < 0) {//左子樹中查找
if (!isRed(node.left) && !isRed(node.left.left)) {
node = moveToRedLeft(node);
}
node.left = delete(node.left, key);
} else if (compare > 0) { //右子樹中查找
if (isRed(node.left)) {
node = rotateRight(node);
}
if (!isRed(node.right) && !isRed(node.right.left)) {
node = moveToRedRight(node);
}
node.right = delete(node.right, key);
} else {
if (Objects.isNull(node.left) && Objects.isNull(node.right)) {
return null; //葉子節(jié)點(diǎn)直接結(jié)束
}
if (Objects.nonNull(node.left)) { //左子樹不為空
Node max = max(node.left);
node.key = max.key;
node.value = max.value;
node.left = deleteMax(node.left);
} else { //右子樹不為空
Node min = min(node.right);
node.key = min.key;
node.value = min.value;
node.right = deleteMin(node.right);
}
}
return balance(node);
}
畫出紅黑樹來驗(yàn)證實(shí)現(xiàn)
上面我們已經(jīng)實(shí)現(xiàn)了紅黑樹的主要代碼,但是如何驗(yàn)證我們的紅黑樹是不是真正的紅黑樹,最好的方式就是基于我們實(shí)現(xiàn)的版本畫出紅黑樹,然后通過紅黑樹的性質(zhì)來驗(yàn)證
由于如何畫出紅黑樹不是本篇的重點(diǎn),所以就不貼出代碼了,有需要的朋友可以去倉庫中查看;
編寫單元來測(cè)試我們用紅黑樹實(shí)現(xiàn)的Map,并且畫出紅黑樹驗(yàn)證是否正確
@Test
public void testDelete() throws IOException {
RedBlack23RedBlackTreeMap<Integer, String> map = new RedBlack23RedBlackTreeMap<>();
map.put(8, "80");
map.put(18, "180");
map.put(5, "50");
map.put(15, "150");
map.put(17, "170");
map.put(25, "250");
map.put(40, "40");
map.put(80, "80");
map.put(30, "30");
map.put(60, "60");
map.put(16, "16");
map.draw("/Users/huaan9527/Desktop/redBlack4.png"); //畫出刪除之前的紅黑樹
map.delete(40);
map.delete(17);
map.delete(25);
map.nodes().forEach(System.out::println); //根據(jù)key從小到大順序打印出節(jié)點(diǎn)
map.draw("/Users/huaan9527/Desktop/redBlack5.png"); //畫出刪除之后的紅黑樹
}
順序打印出node的執(zhí)行的結(jié)果:
刪除之前的紅黑樹
刪除之后的紅黑樹
總結(jié)
本篇主要討論的是基于2-3樹實(shí)現(xiàn)的紅黑樹版本,理解并掌握了本篇內(nèi)容也就掌握了紅黑樹,面試時(shí)根本不虛。
為了加深對(duì)紅黑樹的理解,大家可以自行基于2-3-4樹去實(shí)現(xiàn)紅黑樹,對(duì)比兩種紅黑樹的版本差異,可以參考我的git倉庫中的代碼
文中所有源碼已放入到了github倉庫:https://github.com/silently9527/JavaCore
“給出一個(gè)紅黑樹網(wǎng)站演示,該網(wǎng)站實(shí)現(xiàn)紅黑樹的方式與本篇我們實(shí)現(xiàn)的方式不同,大家可以參考下:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
”
最后(點(diǎn)關(guān)注,不迷路)
文中或許會(huì)存在或多或少的不足、錯(cuò)誤之處,有建議或者意見也非常歡迎大家在評(píng)論交流。
最后,寫作不易,請(qǐng)不要白嫖我喲,希望朋友們可以點(diǎn)贊評(píng)論關(guān)注三連,因?yàn)檫@些就是我分享的全部動(dòng)力來源??