干貨|多起點的局部搜索算法(multi-start local search)解決TSP問題(...
?文案代碼 向柯瑋
?
審核校對 鄧發(fā)珩
前言
各位看客老爺們,大家好~

今天要為大家?guī)淼?code style="font-family:'Operator Mono', Consolas, Monaco, Menlo, monospace;color:rgb(53,148,247);padding-left:2px;">干貨是multi-start local search算法解決TSP問題(Java的實現(xiàn))。
大家可不要因為這個算法的名字比較長,就覺得這個這個算法很難,其實沒有哦-

這個算法還是非常簡單的,希望大家能夠通過這個簡單的算法來了解面對NP-hard問題,我們可以采取的策略是什么。
算法簡介
這個算法,其實大家通過名字就可以知道,一定和Iterated local search(迭代局部搜索算法)存在一定的聯(lián)系。
(這是當(dāng)然呀,名字都差不多,還需要你說嗎?)

迭代局部搜索算法公眾號在之前已經(jīng)介紹過了,有興趣的小伙伴可以再看看~
干貨|迭代局部搜索算法(Iterated local search)探幽(附C++代碼及注釋)??
這兩個算法相似的地方我們就不多說了。我們主要介紹這個算法優(yōu)勢之處。
優(yōu)勢
這種算法,他是多起點的,初始解的生成和遺傳算法挺類似的。
通過隨機打亂,生成多個隨機新解,以此來增大達(dá)到最優(yōu)解的目的。

可能大家光這么看,沒啥感覺,我們可以通過數(shù)學(xué)公式來讓大家直觀的感受一下。
我們認(rèn)為有N個城市,令傳統(tǒng)的LS搜索的次數(shù)為A,傳統(tǒng)的MLS搜索次數(shù)為A',改進(jìn)過的MLS搜索次數(shù)為A'',可以容易得出下面的公式。
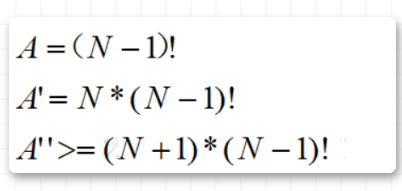
現(xiàn)在讓我們再來看看實際的程序跑出來的結(jié)果。
這是傳統(tǒng)的LS。

這是傳統(tǒng)的MLS。

這是咱們優(yōu)化過的MLS。

從以上兩個例子我們可以看出,MLS確實能夠提高單次程序運行獲得優(yōu)質(zhì)解的概率。
那么,下面就讓我們簡單地總結(jié)一下MLS的一些優(yōu)點。
- 如果是在多線程情況下進(jìn)行探索,那么速度和LS是差不多的
- 探尋到最優(yōu)解的概率更大了
- 對于新手來說,也可以更好的學(xué)習(xí)這種多個初始解的思想,便于以后GA等算法的學(xué)習(xí)
雖然本次代碼的展示仍然是采用單線程,但是只要單線程的明白了,多線程其實很容易就變過去了。
算法流程分析
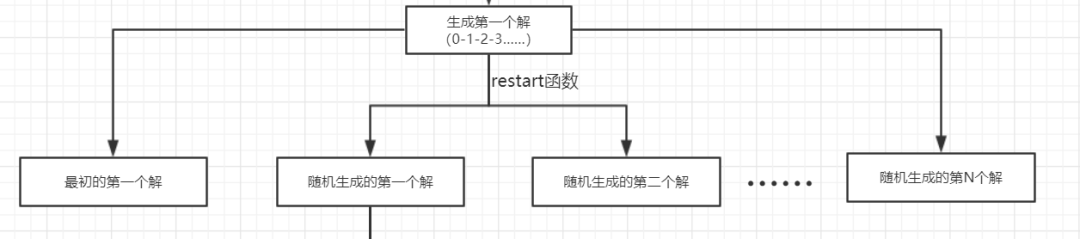
現(xiàn)在我們先來介紹介紹最普遍的一種multi-start local search(多起點的局部搜索算法)。
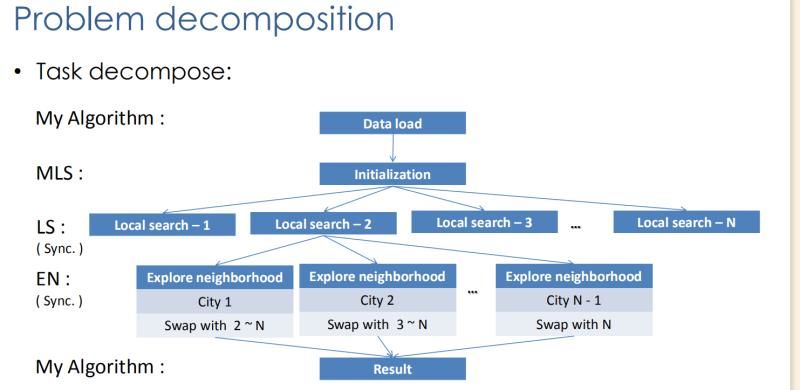
大致的流程就是上面這副圖一樣,在讀取數(shù)據(jù)之后生成第一個解,即按照0-1-2-3……排序的解。
然后將這個解進(jìn)行打亂,生成N組解,然后分別對這N組解利用2-opt算子進(jìn)行鄰域搜索。
我個人感覺這一種multi-start local search算法并不是很好。
- 都是采用的多線程操作,對于新手都不是很友好,代碼不大看得明白
- 算子太少,單一的2-opts算子很難找到較好的解
- 對一些比較差的初始解(通過鄰域搜索都無法找到更好的解),沒有進(jìn)行一些處理
鑒于上面的不足,我對這個算法進(jìn)行了一定程度的改進(jìn)。如下圖。
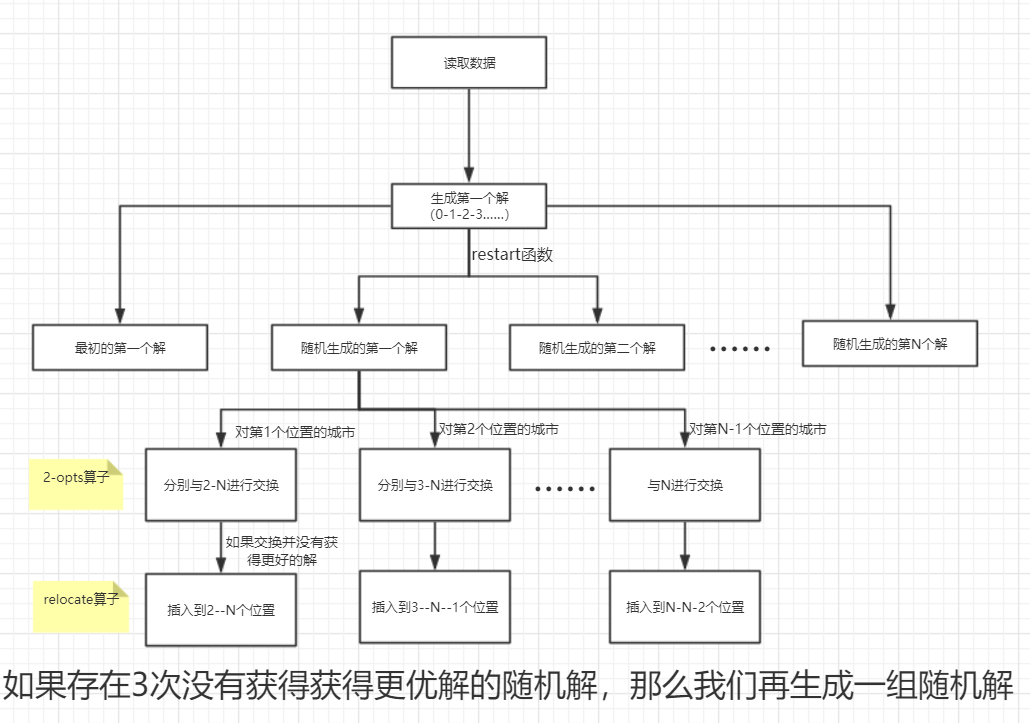

代碼解析
在上面,我們大致的介紹了本次算法的大致實現(xiàn)過程。
接下來,我們對部分代碼進(jìn)行解讀

啟動函數(shù)
這個函數(shù)是我們的main函數(shù),我們在這里完成我們所有的操作。
我們在iter函數(shù)中完成我們的搜索過程。
public class launch {
public static void main(String[] args) {
mls my_solution=new mls(); //生成mls對象
readfile my_file=new readfile(); //讀取文件
my_file.buildInstance("F:\\mls\\data\\uy734.tsp.txt"); //讀取文件
my_solution.setiLSInstance(my_file.getInstance()); //設(shè)置好距離矩陣
my_solution.setsolution(); //設(shè)置好初始解
my_solution.iter(); //開始迭代
my_solution.print_best(); //輸出最優(yōu)解
System.out.println("最佳適應(yīng)度為:"+my_solution.print_of()); //輸出最佳適應(yīng)度
}
}
iter函數(shù)
這個函數(shù)就是最主要的函數(shù),相當(dāng)于整個搜索的過程的啟動器。
我們在這個函數(shù)中,每次生成一個新的隨機解,然后進(jìn)行鄰域搜索。這個就是區(qū)別于LS的根本之處。
并用'tihuan'作為改隨機解是否為一個較好解的標(biāo)志。
public void iter() {
for(int c=0;c
Solution localsolution2 = this.currBest.clone();
for (int j = c; j < this.iLSInstance.getN(); j++) {
Solution now = ls(localsolution2.clone(), j);
if (now.getOF() < this.dLSGlobalBest.getOF())
this.dLSGlobalBest = now.clone();
}
}
for (int i = 0; i < this.iLSInstance.getN(); i++) {
tihuan=false;
Solution localsolution = this.currBest.clone();
localsolution=restart(localsolution);
for (int j = 0; j < this.iLSInstance.getN(); j++) {
Solution now = ls(localsolution.clone(), j);
if (now.getOF() < this.dLSGlobalBest.getOF())
this.dLSGlobalBest = now.clone();
}
for(int m=0;m
System.out.println(localsolution.getsolution().get(this.iLSInstance.getN()-1));
if(!tihuan)
step++;
if(step==50)
{
i--;
step=0;
}
}
}
LS函數(shù)
LS函數(shù),即local search函數(shù),我們通過這個函數(shù),完成我們對每組解的每個位置的城市的鄰域搜索操作。
并用‘tihuan’作為是否生成更好的解(這里是指生成比當(dāng)前隨機解好的解)的標(biāo)志。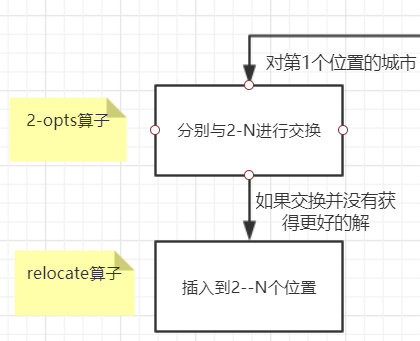
public Solution ls(Solution ssolution,int i) {
Solution best = ssolution.clone();
for (int j = i + 1; j < this.iLSInstance.getN() +i; j++) {
Solution now=ssolution.clone();
if(j
now.setOF(this.cLSCalculator.calc(this.iLSInstance, now));
if (now.getOF() < best.getOF()) {
best = now.clone();
tihuan=true;
}
if(!tihuan){
now.swap(i,j);
now.relocate(i,j);
now.setOF(this.cLSCalculator.calc(this.iLSInstance, now));
if (now.getOF() < best.getOF()) {
best = now.clone();
tihuan=true;
}
}
}
else if(j-this.iLSInstance.getN()
now.setOF(this.cLSCalculator.calc(this.iLSInstance, now));
if (now.getOF() < best.getOF()) {
best = now.clone();
tihuan=true;
}
}
}
return best;
}
restart函數(shù)
這個是我們用來生成隨機新解的函數(shù)。
public Solution restart(Solution solution){
int[]haveset=new int[iLSInstance.getN()];
haveset[0]=0;
for(int i=0;i
while (haveset[n]!=0)
n=rLSRandom.nextInt(iLSInstance.getN());
solution.getsolution().set(i,n);
haveset[n]=1;
}
solution.setOF(this.cLSCalculator.calc(this.iLSInstance, solution));
return solution;
}
小結(jié)
好了,我們現(xiàn)在把算法的大致流程,主要的代碼都展示了一下,大家可以把自己的data輸進(jìn)去,看看結(jié)果怎么樣,T^T,小瑋得到的結(jié)果都不是很理想--
該算法的隨機性很大,獲得優(yōu)質(zhì)解的難度還是蠻大的。
但是我覺得這個算法從傳統(tǒng)LS變過來給了我們很多啟發(fā),比如說,在尋求最優(yōu)解的時候,我們可以采用多線程來提高尋求最優(yōu)解的效率等等。
我希望大家通過本次推文,能夠了解到鄰域解是如何產(chǎn)生的,以及算法不夠好時的我們可以采用哪些改進(jìn)。
那么在下一次的推文中,會介紹一種船新的組合優(yōu)化解決VRPTW的算法~讓我們一起期待吧!

本篇推文代碼請在公眾號后臺回復(fù)【MLS代碼】獲取(不用輸入【】)
?贊 賞?
長按下方二維碼打賞
感謝您,
支持學(xué)生們的原創(chuàng)熱情!
鄭重承諾
打賞是對工作的認(rèn)可
所有打賞所得
都將作為酬勞支付給辛勤工作的學(xué)生
指導(dǎo)老師不取一文
?
文案 && 編輯:向柯瑋(華中科技大學(xué)管理學(xué)院)
審稿&&修正:鄧發(fā)珩(華中科技大學(xué)管理學(xué)院)
指導(dǎo)老師:秦虎(華中科技大學(xué)管理學(xué)院)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
如對文中內(nèi)容有疑問,歡迎交流。PS:部分資料來自網(wǎng)絡(luò)。
如有需求,可以聯(lián)系:
秦虎老師([email protected])
向柯瑋(華中科技大學(xué)管理學(xué)院本科一年級:[email protected])
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
掃一掃,獲取數(shù)據(jù)和模型還有更多算法學(xué)習(xí)課件分享喲