使用深度優(yōu)先搜索算法解決迷宮問題

下面是一個簡單的小迷宮,其中藍色方塊代表墻壁,白色方塊代表道路,你能找到從這個迷宮的入口到出口的路徑嗎?
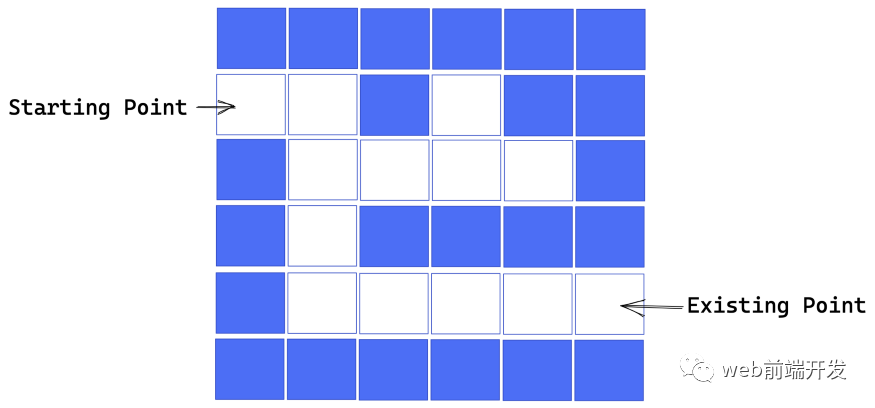
你可能會說:這太簡單了,迷宮的解法我一眼就能搞定。
確實,上面的迷宮很簡單。但是,如果給你這樣一個迷宮,你還能找到它的解決方案嗎?

面對這樣的迷宮,你可能無法一眼就得到迷宮的解法,對你來說可能還需要考慮一段時間。
現(xiàn)在,如果您要編寫一個程序來自動解決迷宮,您將如何編寫代碼?
分析
事實上,當我們解決這類問題時,我們不能想當然。我們應(yīng)該使用標準化的語言來描述我們的想法,然后將這個想法編程為代碼。
對于所有的迷宮問題,可以用一個很簡單的思路來解題,那就是遍歷。
我們可以從起點開始:
首先,判斷當前點是否為已有點。如果是,就意味著我們已經(jīng)找到了終點;如果不是,那么我們需要繼續(xù)遍歷。
然后去正確的地方,并重復步驟 1。
然后轉(zhuǎn)到它的下面點,并重復步驟 1。
然后去它的左邊點,并重復步驟 1。
然后轉(zhuǎn)到上面的點,并重復步驟 1。
如果這個過程是用偽代碼描述的,它看起來像這樣
function solvePoint(x, y) {if Point(x, y) is the existing point:we get the existing point.else:solvePoint(x + 1, y)solvePoint(x, y - 1)solvePoint(x - 1, y)solvePoint(x, y + 1)}
我們可以發(fā)現(xiàn),這個過程實際上包含了一個遞歸過程。
當然,上述步驟中沒有考慮邊界條件和重復訪問。但這是次要的,我們可以稍后添加。
但不管怎樣,通過以上步驟,我們可以遍歷整個迷宮,找到出口的位置。
這樣的步驟看似繁瑣,其實是最有效的方法。而對于計算來說,穿越迷宮的任務(wù)非常簡單,可以很快完成。
解決小迷宮
我們可以將上述想法應(yīng)用到小迷宮中。
首先,我們從起點出發(fā),發(fā)現(xiàn)這個點不是現(xiàn)有的點,所以我們需要在這個點的上下左右上下左右。然后我們發(fā)現(xiàn)起點的上、下、左都不是合法道路,所以只能往右走。
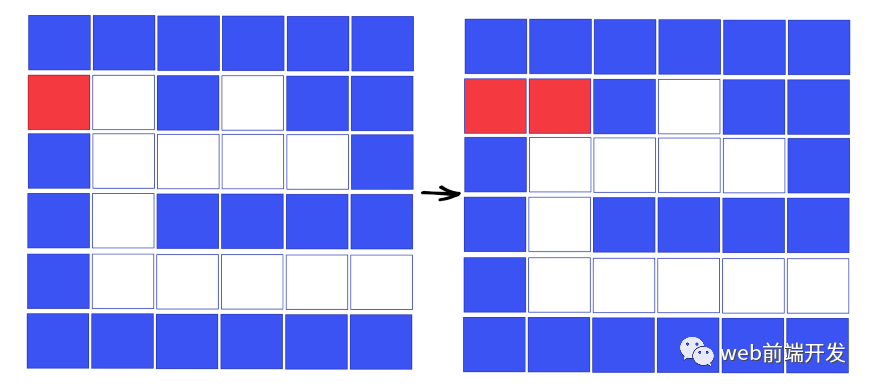
然后我們需要往下走:
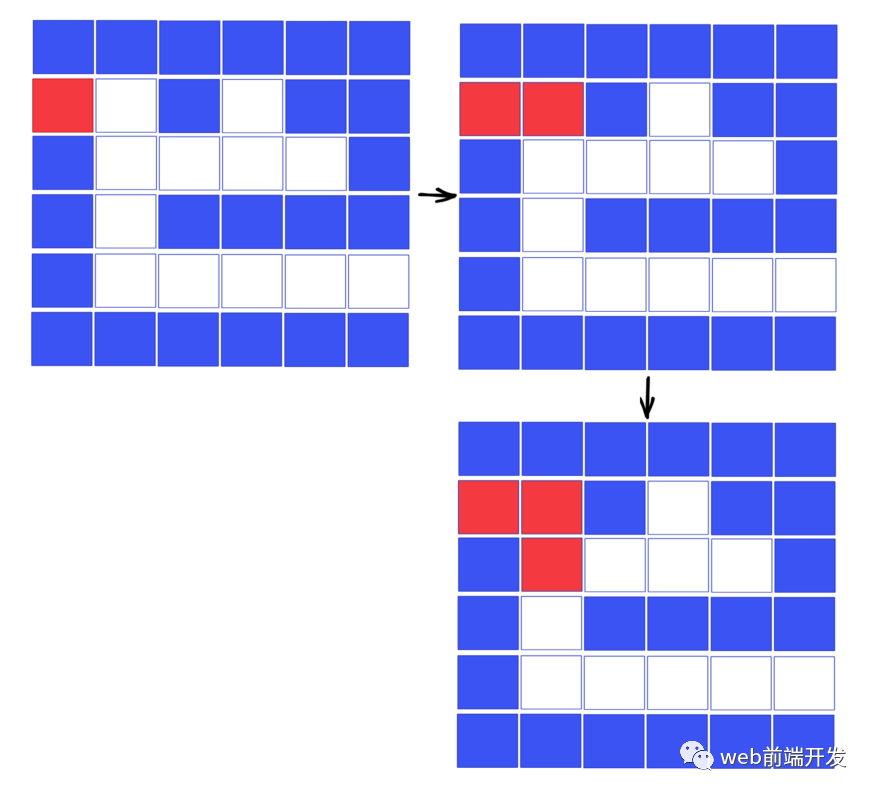
這時候,我們發(fā)現(xiàn)其實有兩個選擇:可以向右走,也可以向下走。而只要我們嘗試所有可能的路徑,最終我們一定會找到解決方案。
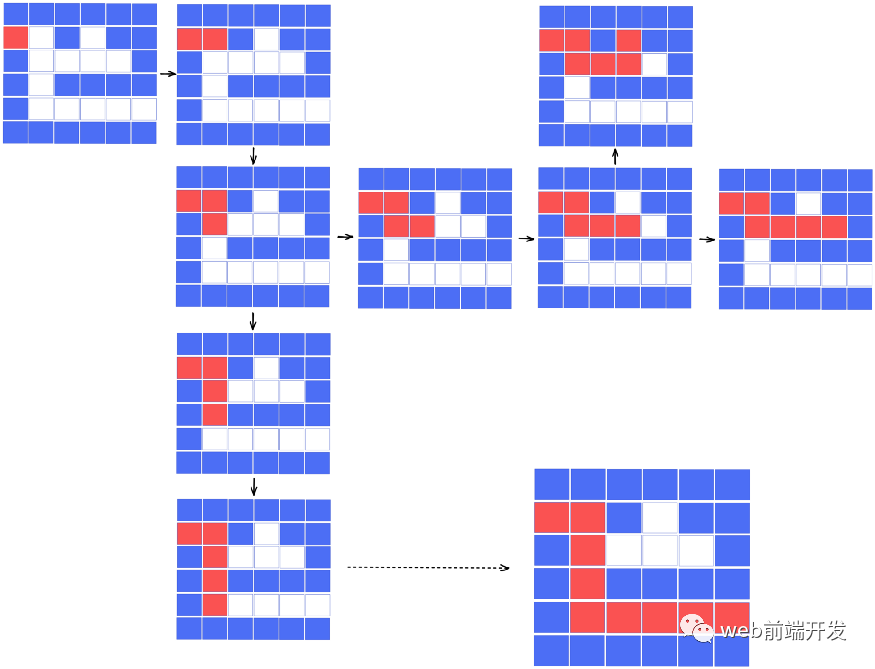
代碼實現(xiàn)
以上是我們的想法,很簡單。一句話總結(jié)就是:按照一定的順序遍歷整個迷宮的所有可能路徑,你一定會到達存在點并找到解決方案。
通過這個算法解迷宮的代碼放在目錄solution/DFS-Recursive中:https://github.com/BytefishMedium/MazeGame
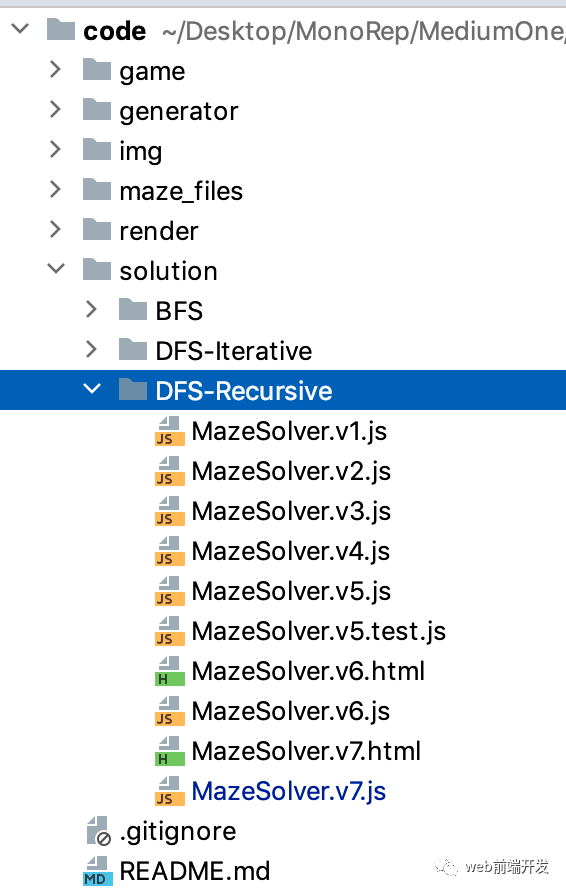
然后,為了方便讀者更好的理解相關(guān)代碼,我將代碼分為v1到v7版本。v1是基本代碼框架,v7是最終完整代碼。
在本文中,我介紹了如何使用數(shù)組來表示迷宮,以及如何使用 Canvas 來渲染迷宮。
v1
首先,我們要明確一件事,那就是我們的終極目標。
在我們的迷宮求解問題中,我們需要以下數(shù)據(jù)作為輸入:迷宮數(shù)組、入口坐標和出口坐標。那么,我們的算法應(yīng)該返回一個點數(shù)組,這個數(shù)組表示從入口到出口的路徑:
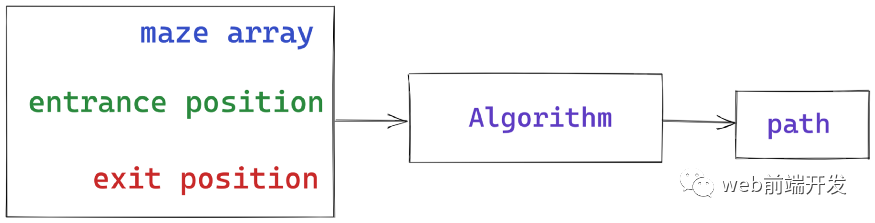
正如我之前所說,我們使用二維數(shù)組來表示迷宮。既然我們的目標是解迷宮,那么我們肯定需要一個迷宮數(shù)組作為參數(shù)。
然后我們需要知道入口坐標。為方便起見,本項目始終使用第二行第一列的點,即坐標為(0, 1)的點作為迷宮的入口。
我們還需要知道現(xiàn)有點的坐標。為方便起見,本項目始終使用倒數(shù)第二行和最后一列中的點作為出口。即坐標為{mazeArray[0].length — 1, mazeArray.length — 2}的點。
最后,我們使用編程語言 JavaScript。JavaScript 支持函數(shù)式編程和面向?qū)ο蟮木幊獭T谖业膶嵺`中,我發(fā)現(xiàn)這個項目的代碼會涉及到很多變量和實用函數(shù),所以我認為使用類表示法更方便。
好的,基本的代碼框架是:
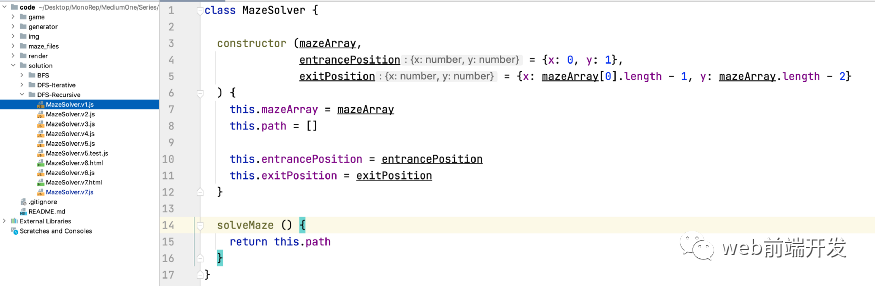
class MazeSolver {constructor (mazeArray,entrancePosition = {x: 0, y: 1},exitPosition = {x: mazeArray[0].length - 1, y: mazeArray.length - 2}) {this.mazeArray = mazeArraythis.path = []this.entrancePosition = entrancePositionthis.exitPosition = exitPosition}solveMaze () {return this.path}}
因為我們的目的是解決迷宮問題,所以我們定義了一個名為 MazeSolver 的類。在構(gòu)造函數(shù)中,我們要求調(diào)用者傳入迷宮數(shù)組、入口坐標、出口坐標等信息。由于我們之前約定一般使用固定的出入口,所以我們會給這兩個參數(shù)一個默認值。
然后我們用this.path來存儲迷宮的最終解法,然后solveMaze就是解迷宮的方法。
v2
然后我們在之前的偽代碼中說過,解迷宮的本質(zhì)就是遍歷迷宮。如果某個點不是現(xiàn)有點,則嘗試訪問該點周圍的點:上、下、左、右。
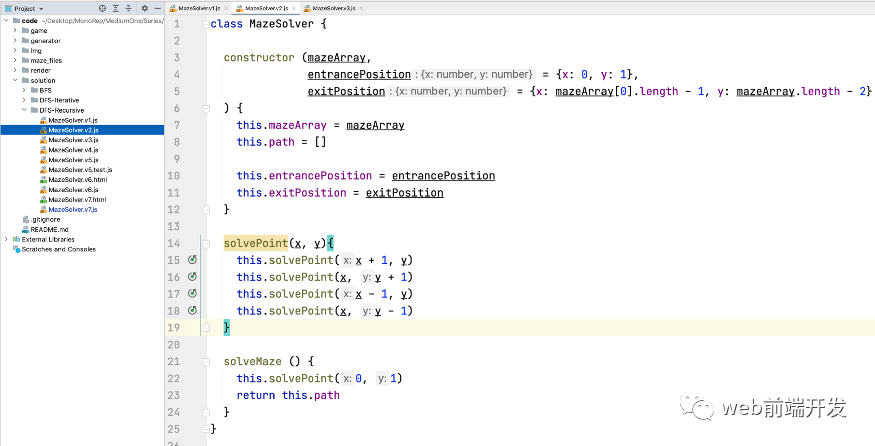
所以當我們的代碼的v2版本是用遞歸來解決它的上、下、左、右點時:
class MazeSolver {constructor (mazeArray,entrancePosition = {x: 0, y: 1},exitPosition = {x: mazeArray[0].length - 1, y: mazeArray.length - 2}) {this.mazeArray = mazeArraythis.path = []this.entrancePosition = entrancePositionthis.exitPosition = exitPosition}solvePoint(x, y){this.solvePoint(x + 1, y)this.solvePoint(x, y + 1)this.solvePoint(x - 1, y)this.solvePoint(x, y - 1)}solveMaze () {this.solvePoint(0, 1)return this.path}}
在這里,我們從起點solvePoint(0,1)開始,然后將四個點向左、上、右、下循環(huán)。
其實這里有個小問題,就是我們遍歷周圍四個點的時候,是按什么順序來的?是上、下、左、右,還是下、左、右、上?這不影響最終的結(jié)果,但確實影響了具體的過程。我們將在可視化部分討論差異,并在此處留下懸念。
那么上面的代碼中沒有考慮邊界問題和終止條件,我們現(xiàn)在繼續(xù)。
v3
這種遍歷的終止條件是到達出口。所以我們只需要簡單的添加一個判斷來判斷當前點是否是現(xiàn)有點。
class MazeSolver {constructor (mazeArray,entrancePosition = {x: 0, y: 1},exitPosition = {x: mazeArray[0].length - 1, y: mazeArray.length - 2}) {this.mazeArray = mazeArraythis.path = []this.entrancePosition = entrancePositionthis.exitPosition = exitPosition}solvePoint(x, y){if (x === this.exitPosition.x && y === this.exitPosition.y) {console.log('you win')return}this.solvePoint(x + 1, y)this.solvePoint(x, y + 1)this.solvePoint(x - 1, y)this.solvePoint(x, y - 1)}solveMaze () {this.solvePoint(0, 1)return this.path}}
v4
但是一個點周圍的四個點不一定都是合法的道路,有可能是越界,或者這個點是一堵墻。所以我們在遞歸的時候,還是需要判斷一個點是否是合法的路。
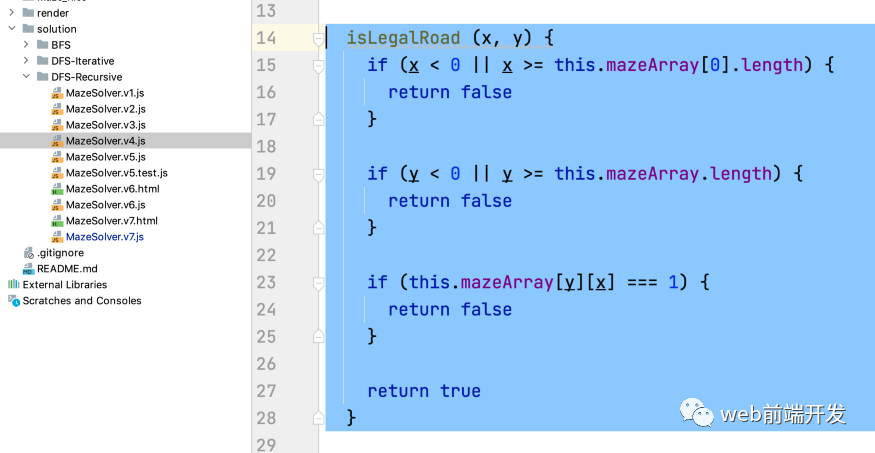
判斷條件很簡單:
橫坐標是否越界
縱坐標是否超出范圍
這個點是不是墻
然后在遞歸之前,判斷下一點是否合法:
class MazeSolver {constructor (mazeArray,entrancePosition = {x: 0, y: 1},exitPosition = {x: mazeArray[0].length - 1, y: mazeArray.length - 2}) {this.mazeArray = mazeArraythis.path = []this.entrancePosition = entrancePositionthis.exitPosition = exitPosition}isLegalRoad (x, y) {if (x < 0 || x >= this.mazeArray[0].length) {return false}if (y < 0 || y >= this.mazeArray.length) {return false}if (this.mazeArray[y][x] === 1) {return false}return true}solvePoint(x, y){if (x === this.exitPosition.x && y === this.exitPosition.y) {console.log('you win')return}if(this.isLegalRoad(x + 1, y)){this.solvePoint(x + 1, y)}if(this.isLegalRoad(x, y + 1)){this.solvePoint(x, y + 1)}if(this.isLegalRoad(x - 1, y)){this.solvePoint(x - 1, y)}if(this.isLegalRoad(x, y - 1)){this.solvePoint(x, y - 1)}}solveMaze () {this.solvePoint(0, 1)return this.path}}
v5
除了判斷點是否合法外,我們還要處理重復訪問的問題。在上面的代碼中,我們沒有考慮重復訪問某個點的問題,所以在遞歸過程中可能會導致重復訪問某個點,導致死循環(huán)。
為了解決這個問題,我們必須記錄訪問過的點,然后在遞歸到下一個點之前進行判斷。
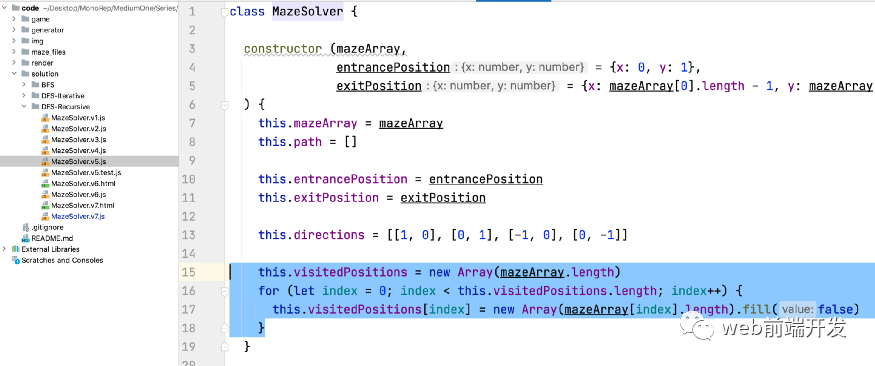
visitedPosition 是一個與迷宮數(shù)組中的點對應(yīng)的二維數(shù)組,它的值是一個布爾值。如果為false,則表示迷宮中的對應(yīng)點沒有被訪問過;如果為真,則說明迷宮中的對應(yīng)點已經(jīng)被訪問過。
稍后,當我們遍歷下一個點時,我們可以做一個額外的判斷:

在這里,我們正在討論一種用于優(yōu)化代碼的附加技術(shù)。我們之前的代碼是這樣的:

如果直接修改這段代碼,需要修改4個地方。
但是我們可以發(fā)現(xiàn),這四個點的坐標變化非常規(guī)律。
橫坐標不變,縱坐標加1
橫坐標加1,縱坐標不變
橫坐標不變,縱坐標減1
橫坐標減1,縱坐標不變
就數(shù)字而言,它可能如下所示:
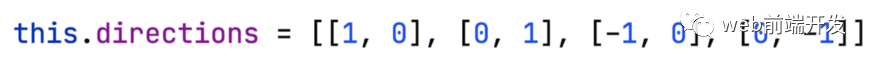
然后我們可以像這樣優(yōu)化代碼:

因為后面我們對里面的代碼還有很多的優(yōu)化,這個小技巧可以方便我們以后改代碼。
完整代碼可以查看相關(guān)源文件:
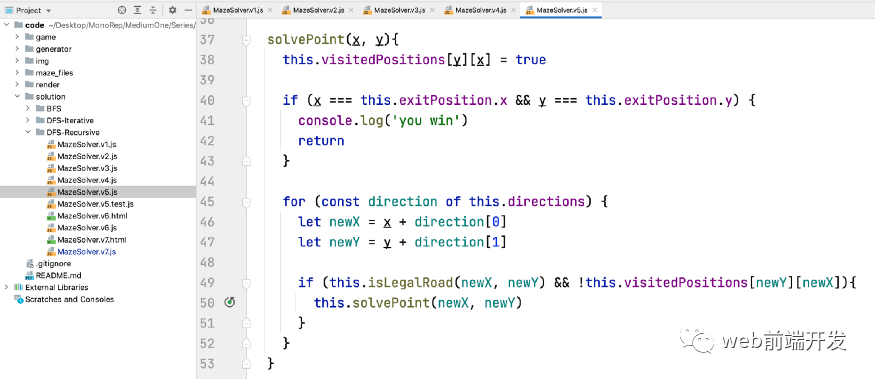
class MazeSolver {constructor (mazeArray,entrancePosition = {x: 0, y: 1},exitPosition = {x: mazeArray[0].length - 1, y: mazeArray.length - 2}) {this.mazeArray = mazeArraythis.path = []this.entrancePosition = entrancePositionthis.exitPosition = exitPositionthis.directions = [[1, 0], [0, 1], [-1, 0], [0, -1]]this.visitedPositions = new Array(mazeArray.length)for (let index = 0; index < this.visitedPositions.length; index++) {this.visitedPositions[index] = new Array(mazeArray[index].length).fill(false)}}isLegalRoad (x, y) {if (x < 0 || x >= this.mazeArray[0].length) {return false}if (y < 0 || y >= this.mazeArray.length) {return false}if (this.mazeArray[y][x] === 1) {return false}return true}solvePoint(x, y){this.visitedPositions[y][x] = trueif (x === this.exitPosition.x && y === this.exitPosition.y) {console.log('you win')return}for (const direction of this.directions) {let newX = x + direction[0]let newY = y + direction[1]if (this.isLegalRoad(newX, newY) && !this.visitedPositions[newY][newX]){this.solvePoint(newX, newY)}}}/**** @return {*}*/solveMaze () {this.solvePoint(0, 1)return this.path}}module.exports = MazeSolver
v5.test
上面的代碼已經(jīng)可以找到迷宮的解法了,我們可以測試一下。具體代碼在 MazeSolver.v5.test.js
const MazeSolver = require('./MazeSolver.v5')function test () {let mazeArray = [[1, 1, 1, 1, 1, 1],[0, 0, 1, 0, 1, 1],[1, 0, 0, 0, 0, 1],[1, 0, 1, 1, 1, 1],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 1],]let mazeSolver = new MazeSolver(mazeArray)mazeSolver.solveMaze()}test()function test2 () {let mazeArray2 = require('../../maze_files/mazeArray101.node.js')let mazeSolver = new MazeSolver(mazeArray2)mazeSolver.solveMaze()}test2()
我們有兩個測試用例,一個是解決小迷宮,另一個是maze_files中的大迷宮。
然后,我們新建一個 MazeSolver 實例,然后調(diào)用它的solveMaze 方法來解迷宮。
最后,我們執(zhí)行完代碼后,在控制臺看到你win打印了兩次,說明我們的程序確實到了結(jié)尾。
v6
雖然已經(jīng)走到了盡頭,但具體的過程我們還是不知道。這時候我們需要添加一些代碼:在遍歷的過程中,記錄解路徑中的點,然后記錄到this.path數(shù)組中。
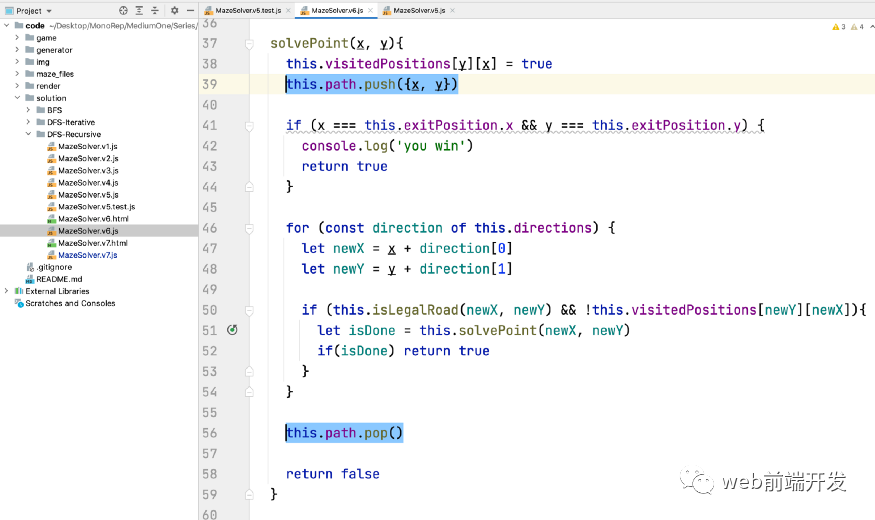
思路也很簡單,就是開始求解某個點的時候,把這個點壓進this.path,記錄下這個位置。
但同時,每個人都需要意識到,有些道路是死胡同。比如上面的小迷宮,在第三個點,它會先向右走,然后發(fā)現(xiàn)是死路,然后又往回走。

所以會有一個回滾過程。回滾時,我們需要通過 this.path.pop() 從路徑數(shù)組中移除這個點。
最后,如果我們的程序到了出口,就不需要繼續(xù)往下遍歷了,我們還要給我們的遞歸加上一個終止條件。

好的,這些是我們最終的遞歸代碼:
有終止條件
有邊界判斷
然后返回一個路徑
class MazeSolver {constructor (mazeArray,entrancePosition = {x: 0, y: 1},exitPosition = {x: mazeArray[0].length - 1, y: mazeArray.length - 2}) {this.mazeArray = mazeArraythis.path = []this.entrancePosition = entrancePositionthis.exitPosition = exitPositionthis.directions = [[1, 0], [0, 1], [-1, 0], [0, -1]]this.visitedPositions = new Array(mazeArray.length)for (let index = 0; index < this.visitedPositions.length; index++) {this.visitedPositions[index] = new Array(mazeArray[index].length).fill(false)}}isLegalRoad (x, y) {if (x < 0 || x >= this.mazeArray[0].length) {return false}if (y < 0 || y >= this.mazeArray.length) {return false}if (this.mazeArray[y][x] === 1) {return false}return true}solvePoint(x, y){this.visitedPositions[y][x] = truethis.path.push({x, y})if (x === this.exitPosition.x && y === this.exitPosition.y) {console.log('you win')return true}for (const direction of this.directions) {let newX = x + direction[0]let newY = y + direction[1]if (this.isLegalRoad(newX, newY) && !this.visitedPositions[newY][newX]){let isDone = this.solvePoint(newX, newY)if(isDone) return true}}this.path.pop()return false}/**** @return {*}*/solveMaze () {let result = this.solvePoint(0, 1)if (result === false) {console.log('no solution for this maze')}return this.path}}function test () {let mazeArray = [[1, 1, 1, 1, 1, 1],[0, 0, 1, 0, 1, 1],[1, 0, 0, 0, 0, 1],[1, 0, 1, 1, 1, 1],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 1],]let mazeSolver = new MazeSolver(mazeArray)let path = mazeSolver.solveMaze()console.log(path)}// test()function test2 () {let mazeArray2 = require('../../maze_files/mazeArray101.node.js')let mazeSolver = new MazeSolver(mazeArray2)let path = mazeSolver.solveMaze()console.log(path)}// test2()
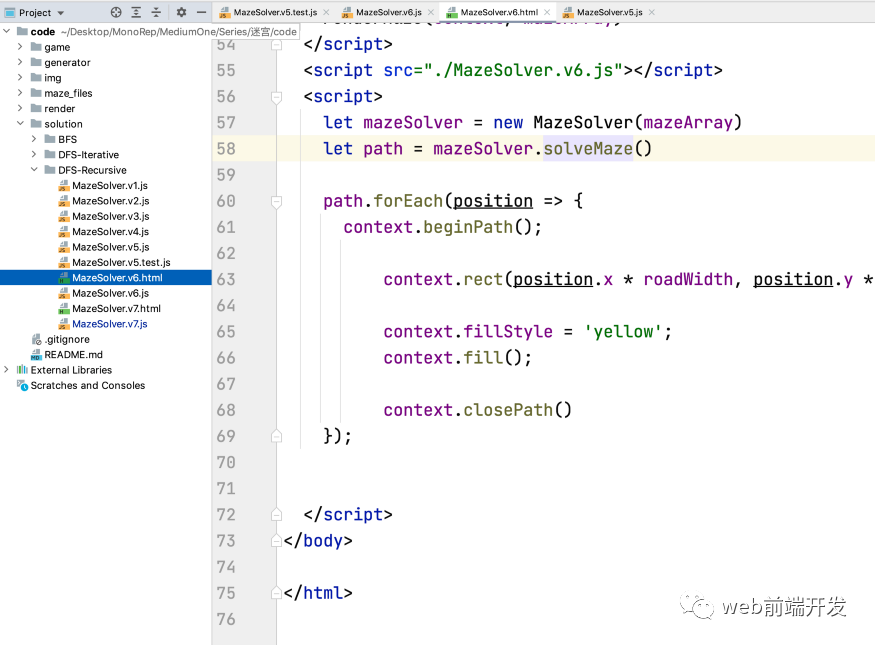
v6.html
現(xiàn)在,我們可以繪制迷宮和路徑:
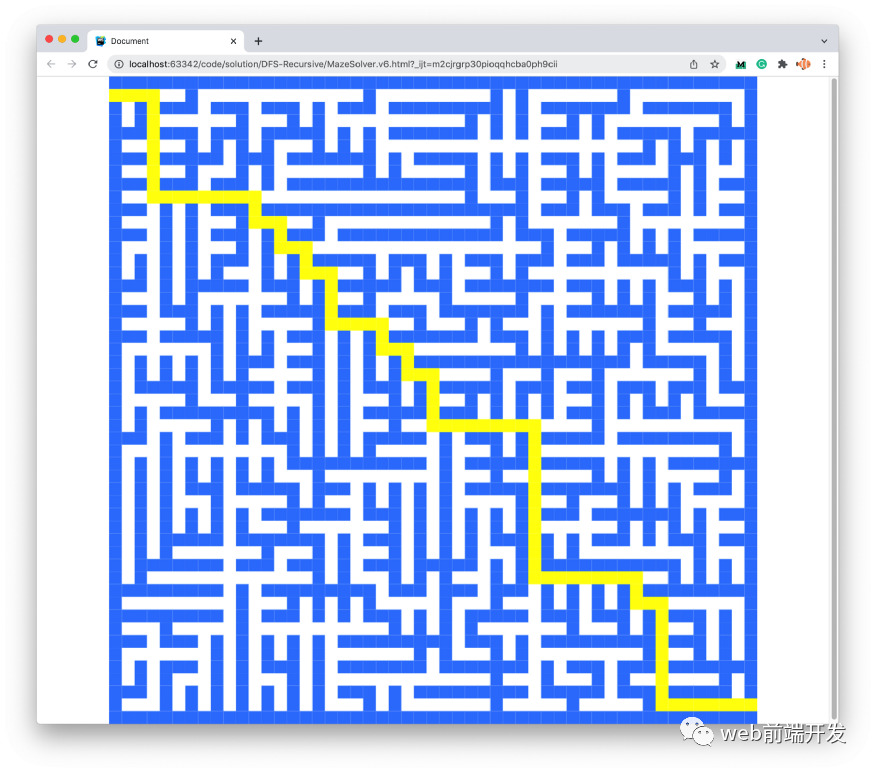
v7
但是上面的代碼只展示了靜態(tài)的結(jié)果,并沒有展示動態(tài)的過程。
我們還想知道的是:算法訪問了哪些點,經(jīng)過了哪些死胡同,最后是如何回歸的。
為了解決這個問題,我們需要繼續(xù)添加代碼。我們添加一個數(shù)組:
//[{type:'enter' , position:{x:0 , y:1}} , {type: 'exit' , position:{x:0 , y:1}}]this.detailedPath = []
截圖如下:
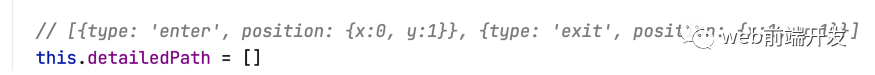
這個數(shù)組不僅記錄了訪問過哪些點,還記錄了是進入還是離開這些點。enter 表示進入,exit 表示離開。
然后,我們在solvePoint方法開始執(zhí)行后標記進入該點,并在結(jié)束前標記離開該點。最終代碼如下:
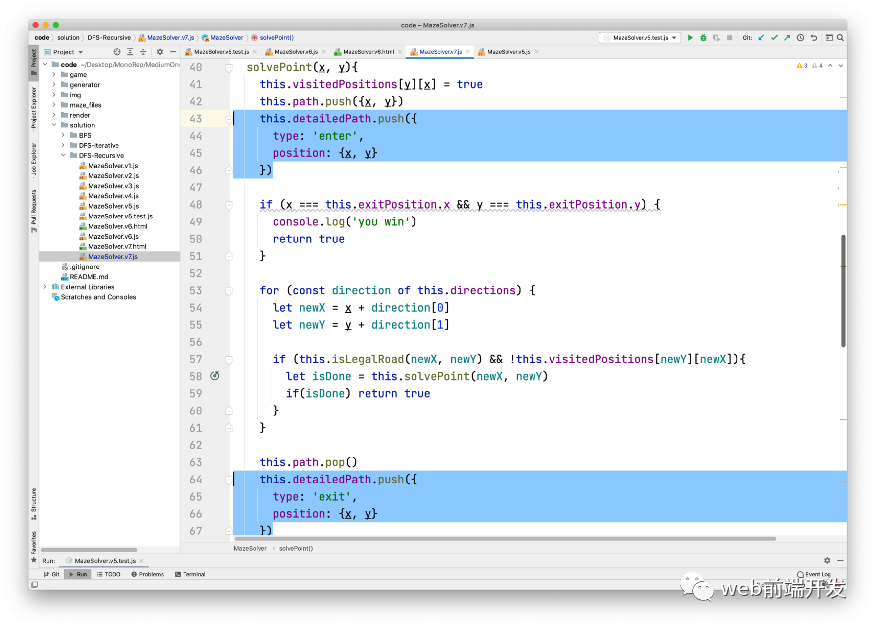
現(xiàn)在,detaillePath 可以記錄算法的具體執(zhí)行過程。
讓我們渲染它:
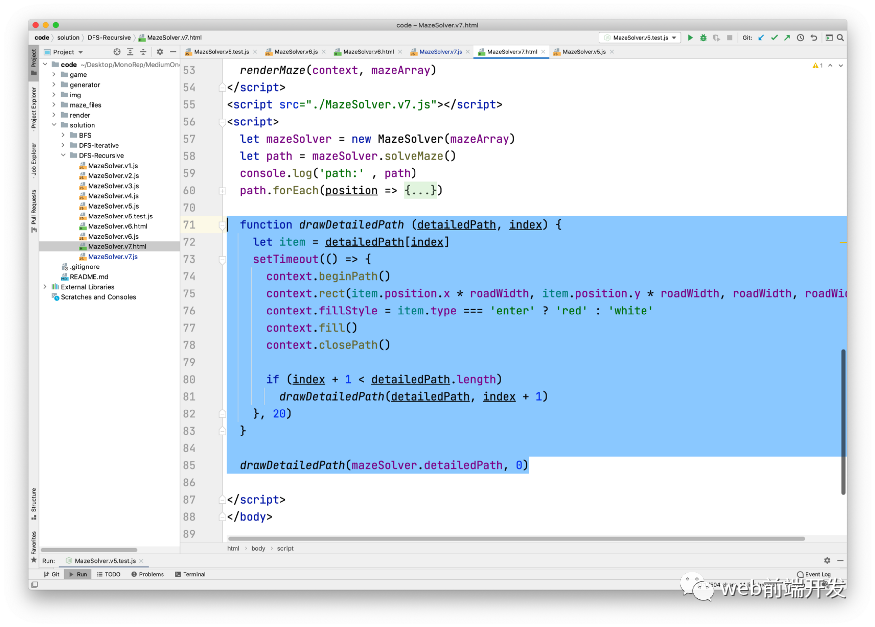
不是很酷嗎?
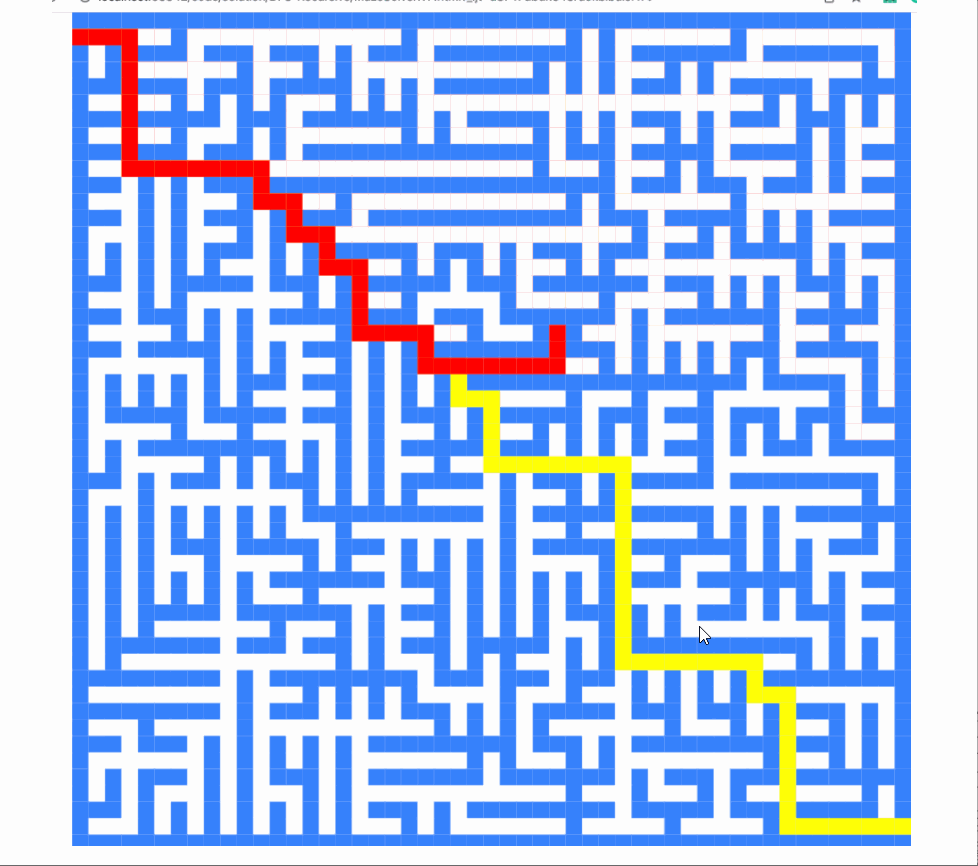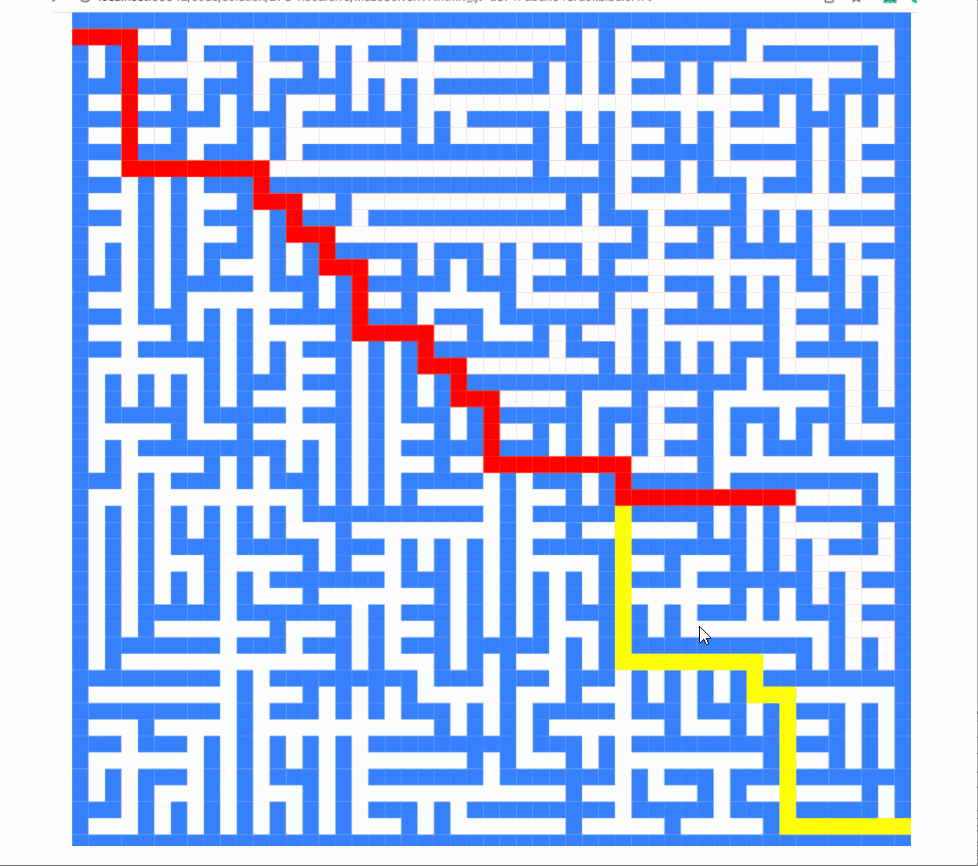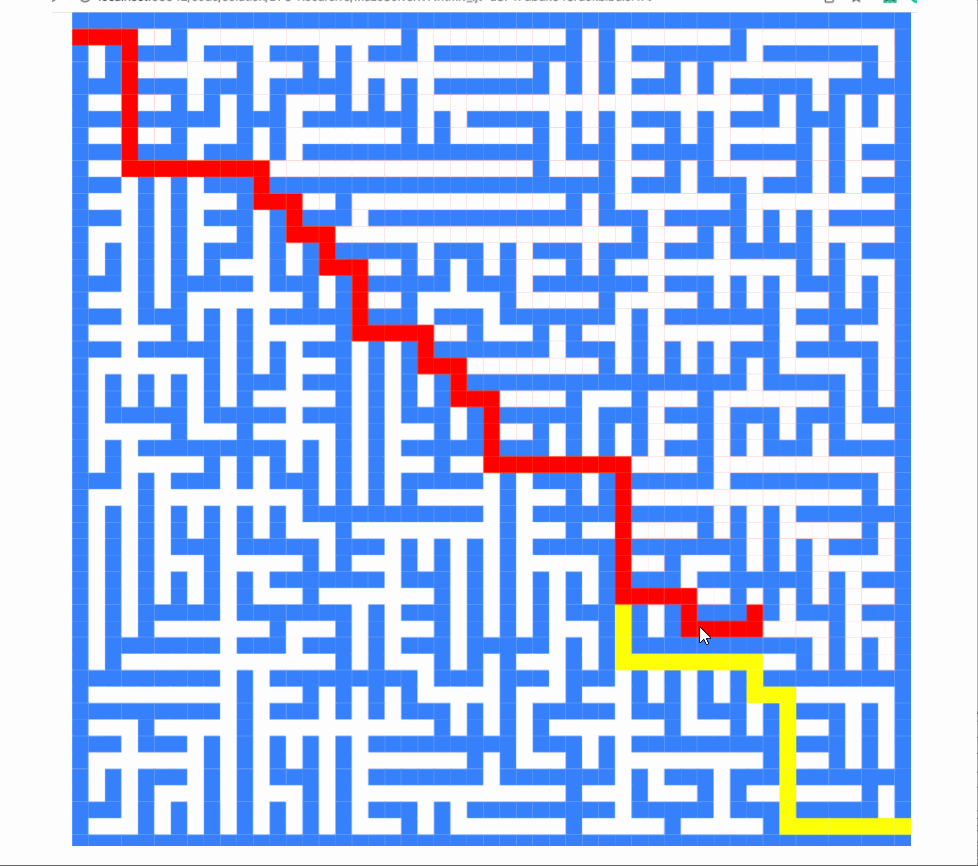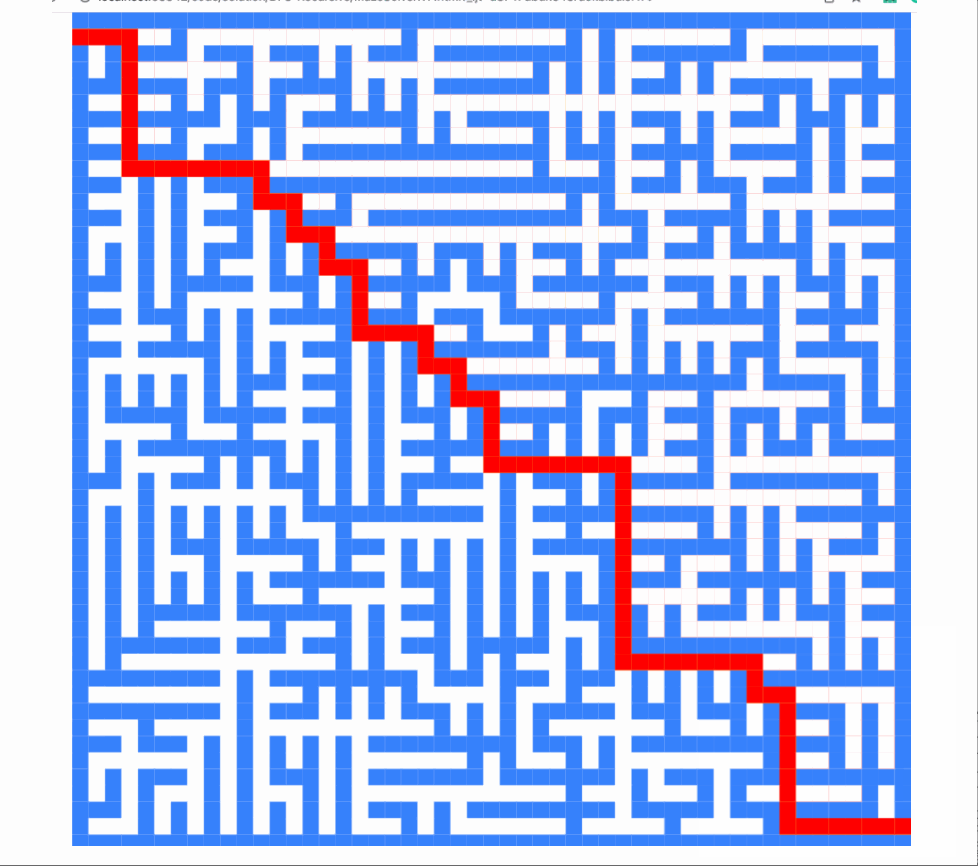
v8
那么,你有沒有注意到算法總是先向左嘗試?
這實際上符合我們之前提到的代碼:

而我們的坐標系是這樣的:
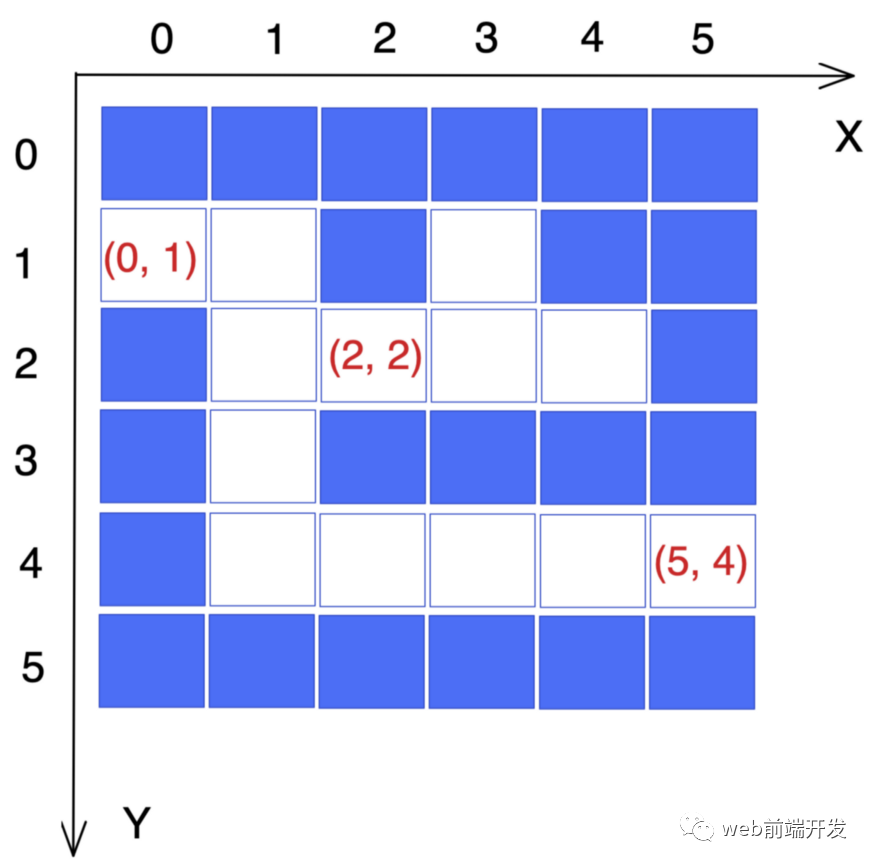
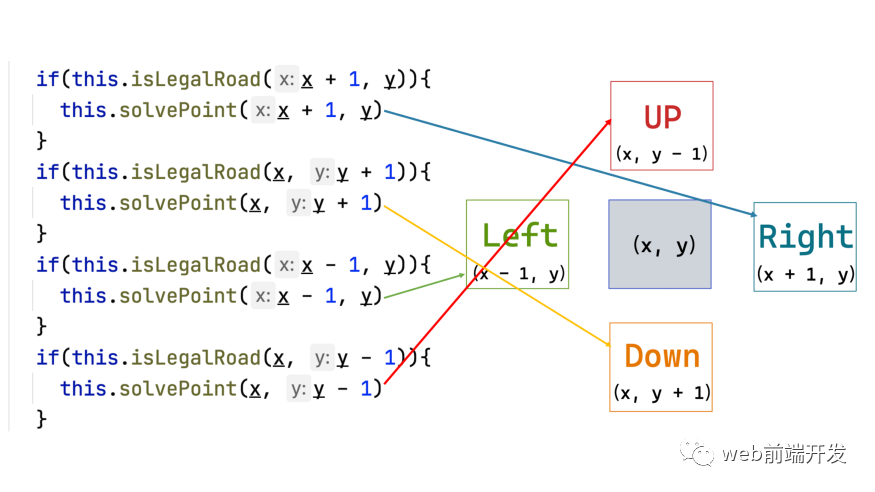
所以在之前的搜索路徑中,我們的算法總是優(yōu)先向右走。
如果要調(diào)整搜索順序,只需要改變以上幾行代碼的順序即可。但是正如我們之前提到的,我們用 this.directions 修改了代碼,所以我們現(xiàn)在可以像這樣修改它:
this.directions = [[-1,0],[0,1],[1,0],[0,-1]]截圖如下:

現(xiàn)在它是:
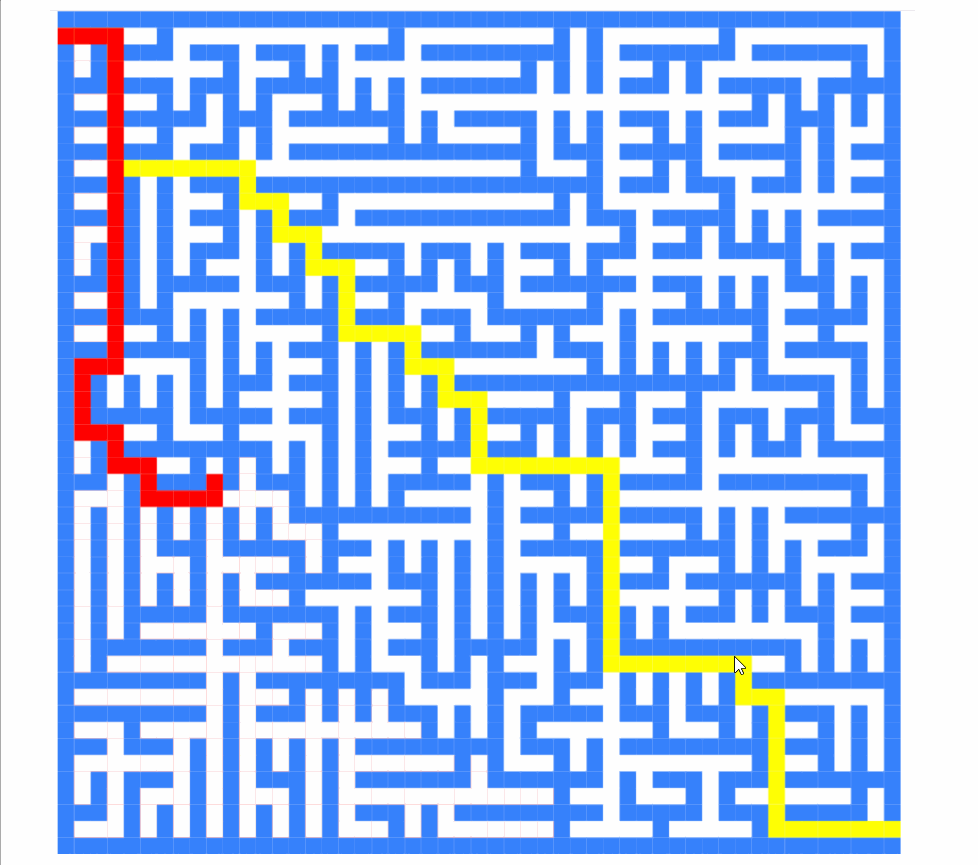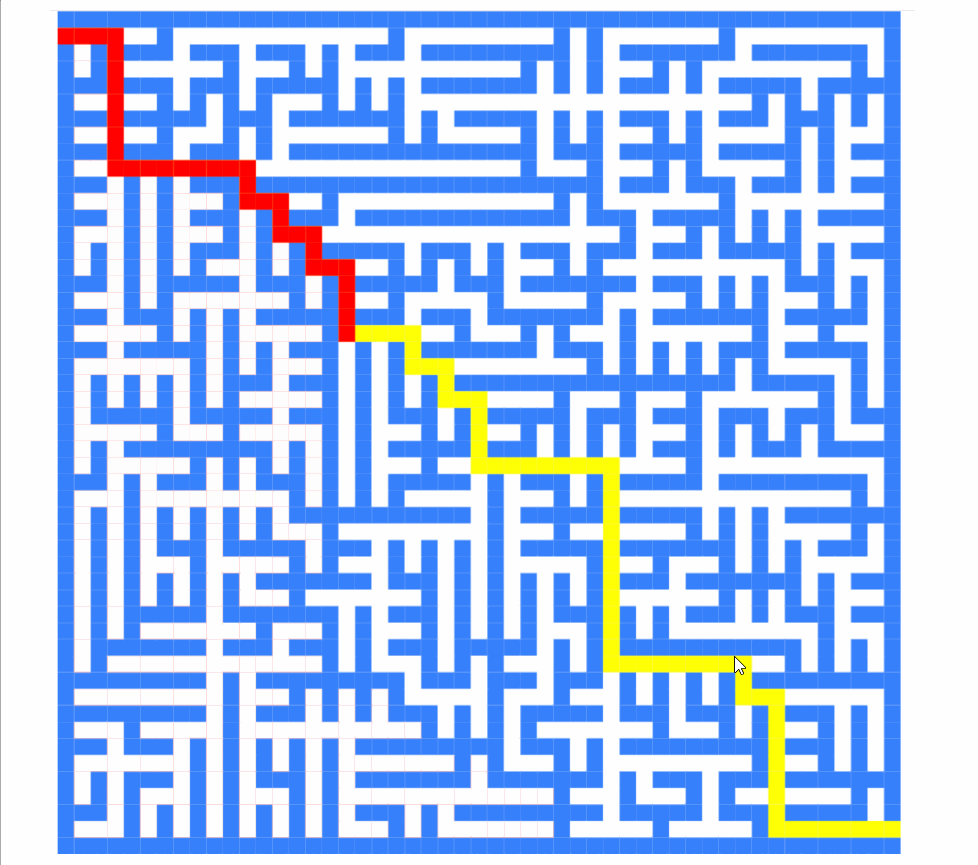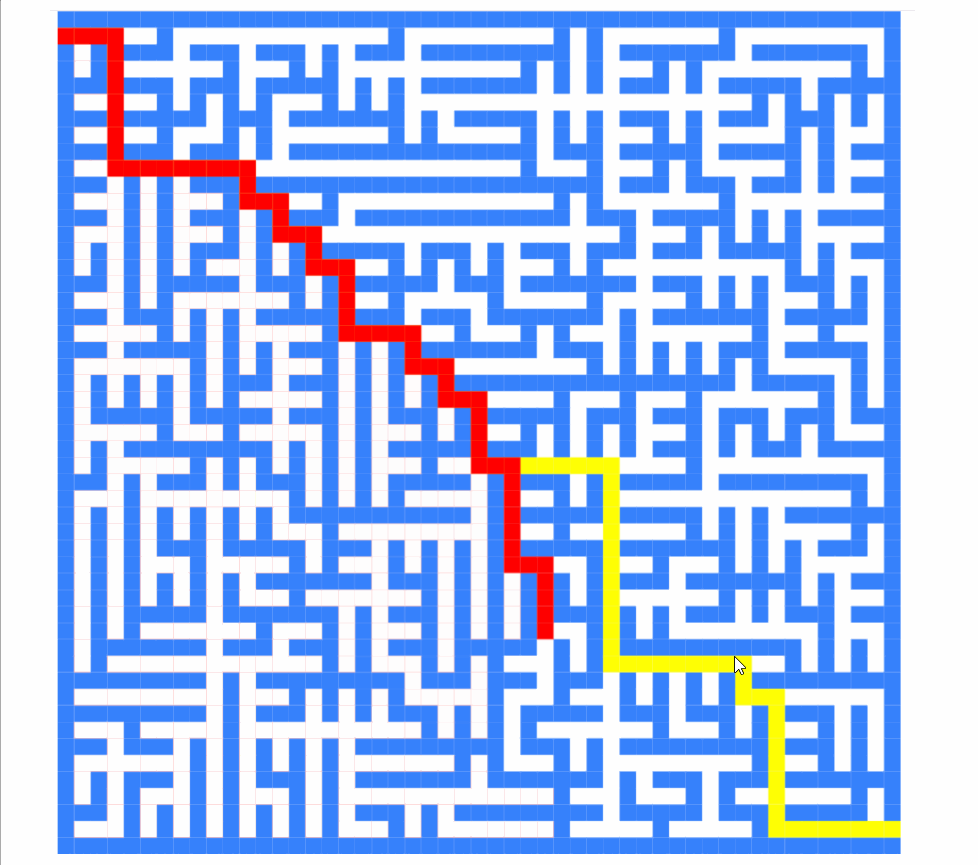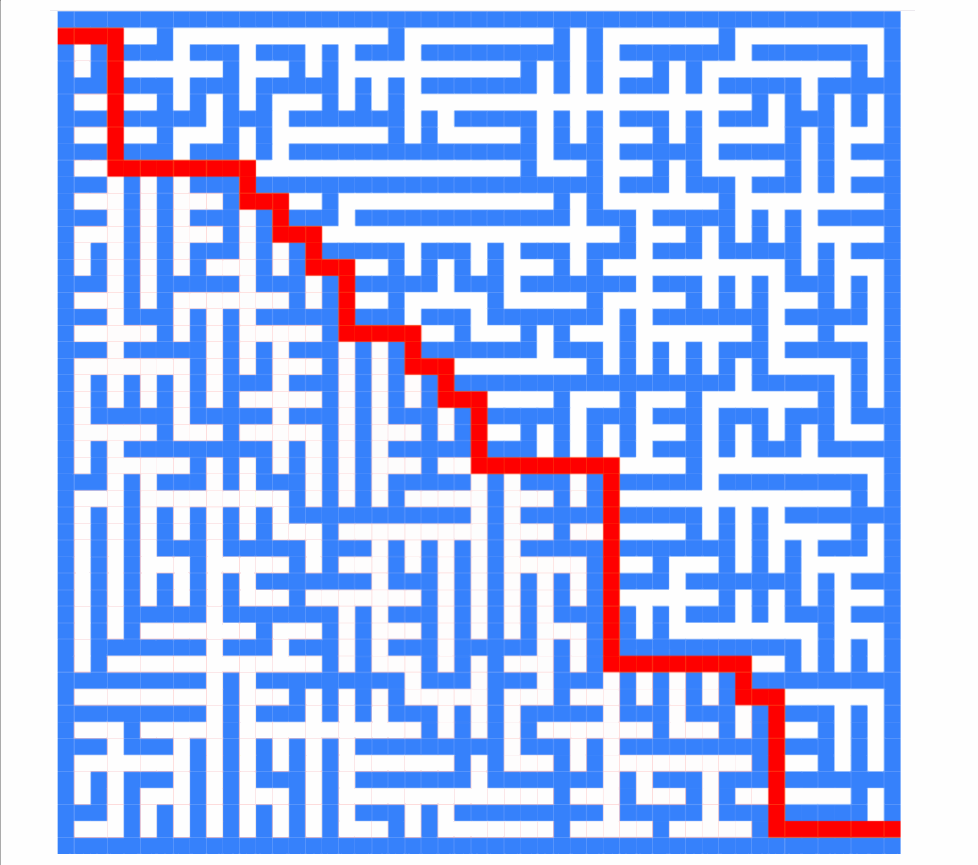
如您所見,算法求解的順序完全不同。
深度優(yōu)先搜索
在這種遍歷算法中,它會先嘗試一條路徑,然后繼續(xù)深入,直到到達死胡同或找到最終解決方案。如果遇到死胡同,將退回到上一點。這種遍歷方法稱為深度優(yōu)先搜索,對應(yīng)的還有廣度優(yōu)先搜索,后面的文章會講到。
結(jié)論
好了,今天的內(nèi)容迷宮,我們就先成功解到這里,我也把整個過程可視化了,希望這個對你學習算法內(nèi)容有幫助,同時也希望通過這個案例,讓你對深度優(yōu)先搜索有了更直觀的認識。
最后,如果你覺得今天的內(nèi)容有用的話,請記得點贊我,關(guān)注我,并將它分享給你身邊做開發(fā)的朋友,也許能夠幫助到他。
感謝你的閱讀,祝編程愉快!
學習更多技能
請點擊下方公眾號
![]()

