計(jì)數(shù)排序真的不重要？

計(jì)數(shù)排序雖然不是面試常考題目，但是計(jì)數(shù)排序的求統(tǒng)計(jì)數(shù)組步驟和最后元素歸位思想是我們刷題時(shí)經(jīng)常用到的，例如原地置換，使用數(shù)組模擬 hashmap 等，所以還是很有必要看一下的。

今天我們就一起來(lái)看看線性排序里的計(jì)數(shù)排序到底是怎么回事吧。

我們將鏡頭切到袁記菜館

因?yàn)榻衲暝洸损^的效益不錯(cuò)，所以袁廚就想給員工發(fā)些小福利，讓小二根據(jù)員工工齡進(jìn)行排序，但是菜館共有 100000  名員工，菜館開業(yè) 10 年，員工工齡從 0 - 10 不等。

看來(lái)這真是一個(gè)艱巨的任務(wù)啊。

當(dāng)然我們可以借助之前說(shuō)過(guò)的 歸并排序 和 快速排序 解決，但是我們有沒(méi)有其他更好的方法呢？

了解排序算法的老哥可能已經(jīng)猜到今天寫什么啦。是滴，我們今天來(lái)寫寫用空間換時(shí)間的線性排序。

說(shuō)之前我們先來(lái)回顧一下之前的排序算法，最好的時(shí)間復(fù)雜度為  O(nlogn) ,且都基于元素之間的比較來(lái)進(jìn)行排序。

我們來(lái)說(shuō)一下非基于元素比較的排序算法，且時(shí)間復(fù)雜度為 O（n），時(shí)間復(fù)雜度是線性的，所以我們稱其為線性排序算法。

其優(yōu)勢(shì)在于在對(duì)一定范圍內(nèi)的整數(shù)排序時(shí)，它的復(fù)雜度為Ο(n+k)，此時(shí)的 k 則代表整數(shù)的范圍。快于任何一種比較類排序算法，不過(guò)也是需要犧牲一些空間來(lái)?yè)Q取時(shí)間。

下面我們先來(lái)看看什么是計(jì)數(shù)排序，這個(gè)計(jì)數(shù)的含義是什么？

我們假設(shè)某一分店共有 10 名員工，

工齡分別為 1，2，3，5，0，2，2，4，5，9

那么我們將其存在一個(gè)長(zhǎng)度為 10 的數(shù)組里，，但是我們注意，我們數(shù)組此時(shí)存的并不是元素值，而是元素的個(gè)數(shù)。見(jiàn)下圖

注：此時(shí)我們這里統(tǒng)計(jì)次數(shù)的數(shù)組長(zhǎng)度根據(jù)最大值來(lái)決定，上面的例子中最大值為 9 ，則長(zhǎng)度為 9 + 1 = 10。暫且先這樣理解，后面會(huì)對(duì)其優(yōu)化 。

我們繼續(xù)以上圖的例子來(lái)說(shuō)明，在該數(shù)組中，索引代表的為元素值（也就是上面例子中的工齡），數(shù)組的值代表的則是元素個(gè)數(shù)（也就是不同工齡出現(xiàn)的次數(shù)）。

即工齡為 0 的員工有 1 個(gè)， 工齡為 1 的員工有 1 個(gè)，工齡為 2 的員工有 3 個(gè) 。。。

然后我們根據(jù)出現(xiàn)次數(shù)將其依次取出看看是什么效果。

0，1，2，2，2，3，4，5，5，9

我們發(fā)現(xiàn)此時(shí)元素則變成了有序的，但是這并不是排序，只是簡(jiǎn)單的按照統(tǒng)計(jì)數(shù)組的下標(biāo)，輸出了元素值，并沒(méi)有真正的給原始數(shù)組進(jìn)行排序。

這樣操作之后我們不知道工齡屬于哪個(gè)員工。

見(jiàn)下圖

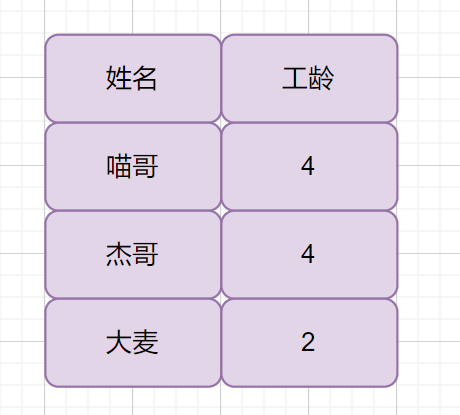
雖然喵哥和杰哥工齡相同，如果我們按照上面的操作輸出之后，我們不能知道工齡為 4 的兩個(gè)員工，哪個(gè)是喵哥哪個(gè)是杰哥。

所以我們需要借助其他方法來(lái)對(duì)元素進(jìn)行排序。

大家還記不記得我們之前說(shuō)過(guò)的前綴和，下面我們通過(guò)上面統(tǒng)計(jì)次數(shù)的數(shù)組求出其前綴和數(shù)組。

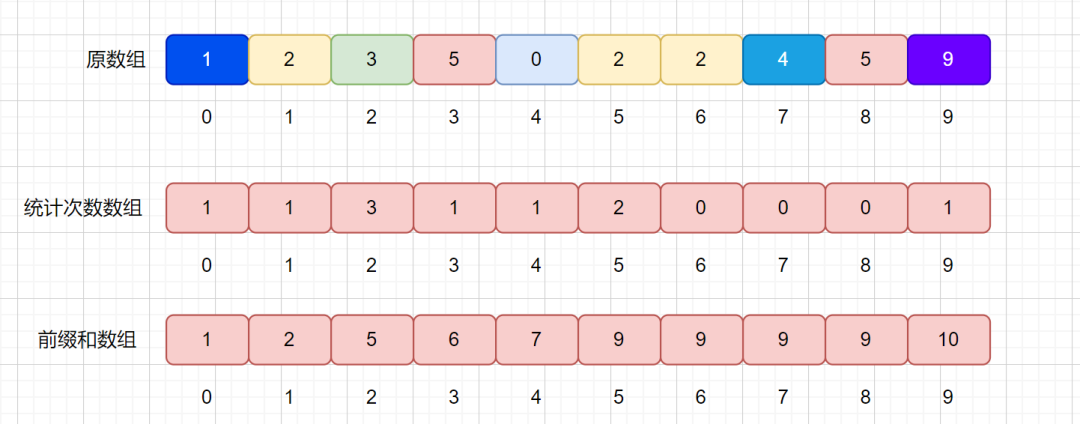
因?yàn)槲覀兪峭ㄟ^(guò)統(tǒng)計(jì)次數(shù)的數(shù)組得到了前綴和數(shù)組，那么我們來(lái)分析一下 presum 數(shù)組里面值的含義。

例如我們的 presum[2]  = 5 ,代表的則是原數(shù)組小于等于 2 的值共有 5 個(gè)。presum[4] = 7 代表小于等于 4 的元素共有 7 個(gè)。

是不是感覺(jué)計(jì)數(shù)排序的含義要慢慢顯現(xiàn)出來(lái)啦。

其實(shí)到這里我們已經(jīng)可以理解的差不多了，還差最后一步，

此時(shí)我們要從后往前遍歷原始數(shù)組，然后將遍歷到的元素放到臨時(shí)數(shù)組的合適位置，并修改 presum 數(shù)組的值，遍歷結(jié)束后則達(dá)到了排序的目的。

這時(shí)有人要問(wèn)了，為什么我們要從后往前遍歷呢？

這個(gè)問(wèn)題的答案，我們等下說(shuō)，繼續(xù)往下看吧。

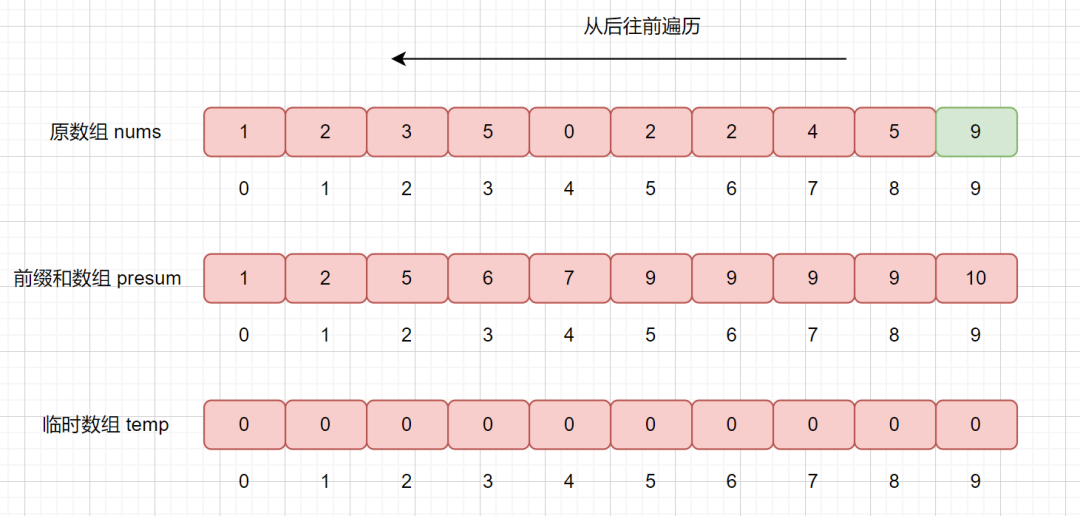
我們從后往前遍歷，nums[9] = 9,則我們拿該值去 presum 數(shù)組中查找，發(fā)現(xiàn) presum[nums[9]] = presum[9] = 10 ，

大家還記得我們 presum 數(shù)組里面每個(gè)值的含義嗎，我們此時(shí) presum[9] = 10,則代表在數(shù)組中，小于等于的數(shù)共有 10 個(gè)，則我們要將他排在臨時(shí)數(shù)組的第 10 個(gè)位置，也就是 temp[9] = 9。

我們還需要干什么呢？我們想一下，我們已經(jīng)把 9 放入到 temp 數(shù)組里了，已經(jīng)對(duì)其排好序了，那么我們的 presum 數(shù)組則不應(yīng)該再統(tǒng)計(jì)他了，則將相應(yīng)的位置減 1 即可，也就是 presum[9] = 10 - 1 = 9;

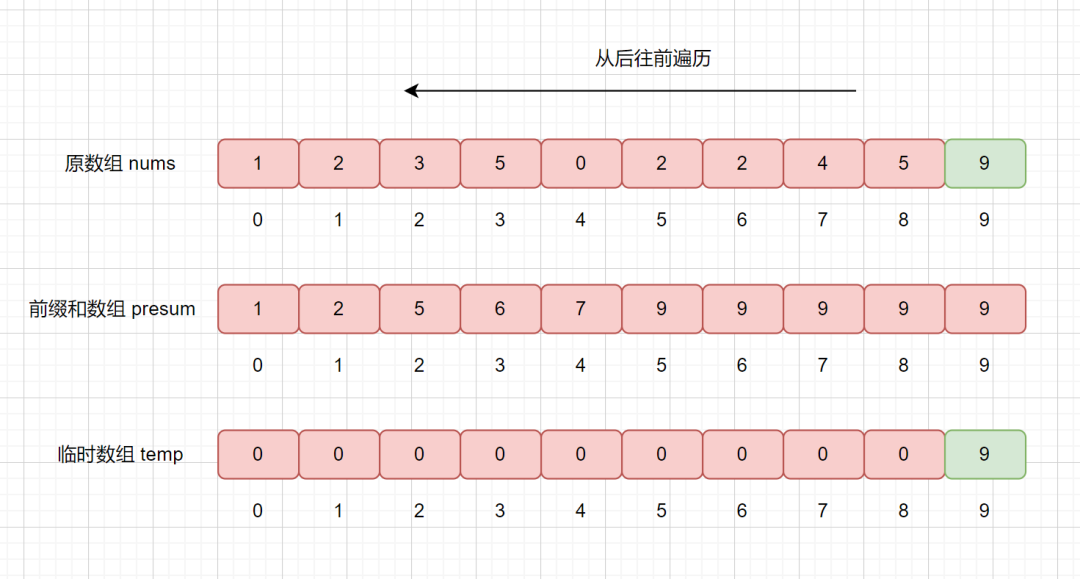
下面我們繼續(xù)遍歷 5 ，然后同樣執(zhí)行上訴步驟

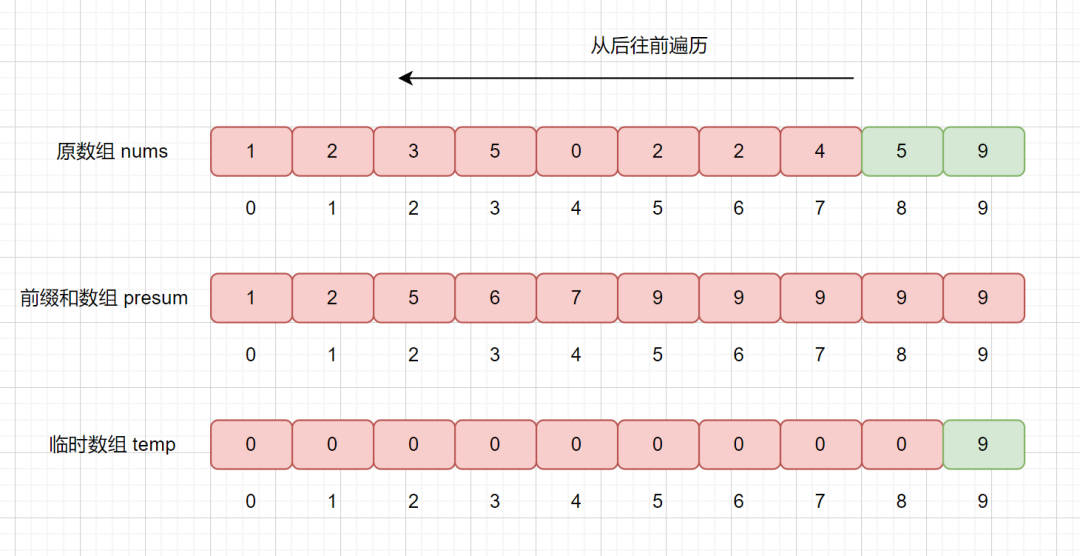
我們繼續(xù)查詢 presum 數(shù)組，發(fā)現(xiàn) presum[5] = 9,則說(shuō)明小于等于 5 的數(shù)共有 9 個(gè)，我們將其放入到 temp 數(shù)組的第 9 個(gè)位置，也就是

temp[8] = 5。然后再將 presum[5] 減 1 。

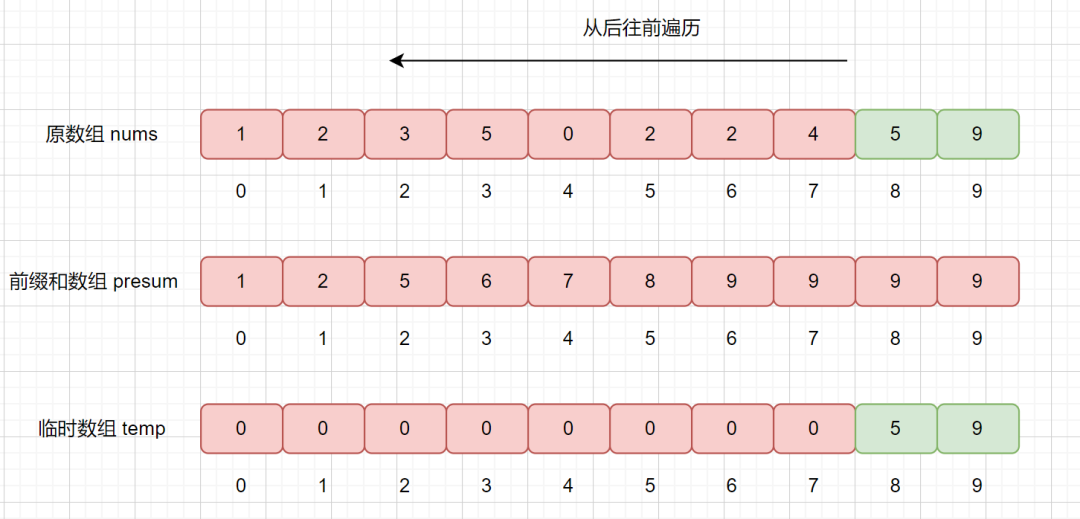
是不是到這里就理解了計(jì)數(shù)排序的大致思路啦。

那么我們?yōu)槭裁葱枰獜暮笸氨闅v呢？我們思考一下，如果我們從前往后遍歷，相同元素的話，前面的元素則會(huì)先歸位再減一，這樣則會(huì)使計(jì)數(shù)排序變成不穩(wěn)定的排序算法。

這個(gè)排序的過(guò)程像不像查字典呢？通過(guò)查詢 presum 數(shù)組，得出自己應(yīng)該排在臨時(shí)數(shù)組的第幾位。然后再修改下字典，直到遍歷結(jié)束。

那么我們先來(lái)用動(dòng)畫模擬一下我們這個(gè) bug 版的計(jì)數(shù)排序，加深理解。

注：我們得到 presum 數(shù)組的過(guò)程在動(dòng)畫中省略。直接模擬排序過(guò)程。

但是到現(xiàn)在就完了嗎？顯然沒(méi)有，我們思考下這個(gè)情況。

假如我們的數(shù)字為   90，93，94，91，92  如果我們根據(jù)上面方法設(shè)置 presum 數(shù)組的長(zhǎng)度，那我們則需要設(shè)置數(shù)組長(zhǎng)度為 95（因?yàn)樽畲笾凳?4），這樣顯然是不合理的，會(huì)浪費(fèi)掉很多空間。

還有就是當(dāng)我們需要對(duì)負(fù)數(shù)進(jìn)行排序時(shí)同樣會(huì)出現(xiàn)問(wèn)題，因?yàn)槲覀兦蟠螖?shù)的時(shí)候是根據(jù) nums[index] 的值來(lái)填充 presum 數(shù)組的，所以當(dāng) nums[index] 為負(fù)數(shù)時(shí)，填充 presum 數(shù)組時(shí)則會(huì)報(bào)錯(cuò)。

此時(shí)通過(guò)最大值來(lái)定義數(shù)組長(zhǎng)度也不合理。

所以我們需要采取別的方法來(lái)定義數(shù)組長(zhǎng)度。

下面我們來(lái)說(shuō)一下偏移量的概念。

例如  90，93，94，91，92，我們 可以通過(guò) max ，min  的值來(lái)設(shè)置數(shù)組長(zhǎng)度即 94 - 90 + 1 = 5 。偏移量則為 min 值，也就是 90。那么我們的 90 則對(duì)應(yīng)索引 0 。

見(jiàn)下圖。

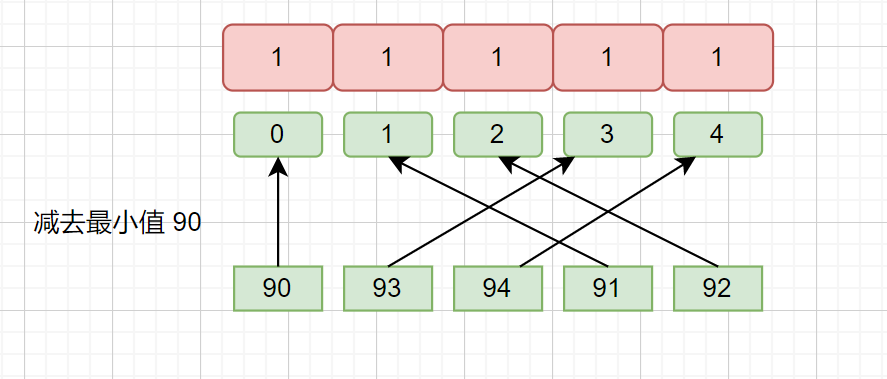
這樣我們填充 presum 數(shù)組時(shí)就不會(huì)出現(xiàn)浪費(fèi)空間的情況了，負(fù)數(shù)？出現(xiàn)負(fù)數(shù)的情況當(dāng)然也可以。繼續(xù)看

例如：-1，-3，0，2，1

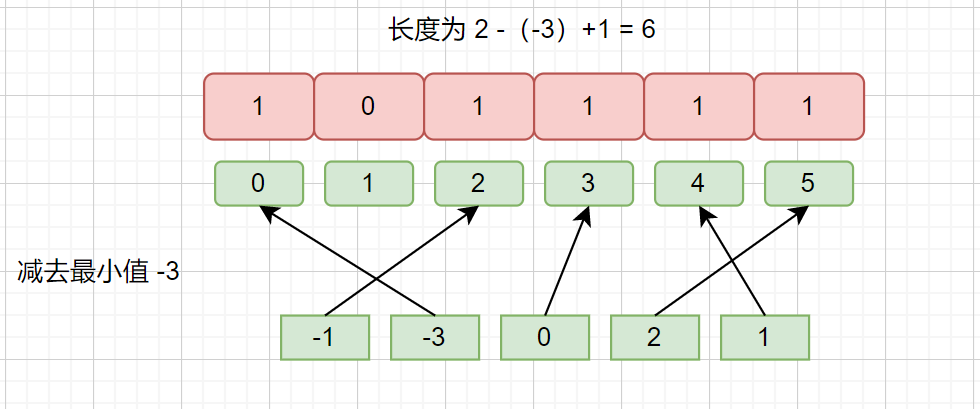
一樣可以，哦了，到這里我們就搞定了計(jì)數(shù)排序，下面我們來(lái)看一哈代碼吧。

class Solution {
    public int[] sortArray(int[] nums) {

        int len = nums.length;
        if (nums.length < 1) {
             return nums;
        }
        //求出最大最小值
        int max = nums[0];
        int min = nums[0];
        for (int x : nums) {
            if (max < x)  max = x;       
            if (min > x)  min = x;         
        }
        //設(shè)置 presum 數(shù)組長(zhǎng)度,然后求出我們的前綴和數(shù)組，
        //這里我們可以把求次數(shù)數(shù)組和前綴和數(shù)組用一個(gè)數(shù)組處理
        int[] presum = new int[max-min+1];
        for (int x : nums) {
            presum[x-min]++;
        }
        for (int i = 1; i < presum.length; ++i) {
            presum[i] = presum[i-1]+presum[i]; 
        }
        //臨時(shí)數(shù)組
        int[] temp = new int[len];
        //遍歷數(shù)組，開始排序,注意偏移量
        for (int i = len-1; i >= 0; --i) {
            //查找 presum 字典，然后將其放到臨時(shí)數(shù)組，注意偏移度
            int index = presum[nums[i]-min]-1;
            temp[index] = nums[i];
            //相應(yīng)位置減一
            presum[nums[i]-min]--;           
        }
        //copy回原數(shù)組
        System.arraycopy(temp,0,nums,0,len);
        return nums;
    }
}

好啦，這個(gè)排序算法我們已經(jīng)搞定了，下面我們來(lái)扒一扒它。

計(jì)數(shù)排序時(shí)間復(fù)雜度分析

我們的總體運(yùn)算量為 n+n+k+n ，總體運(yùn)算是 3n + k 所以時(shí)間復(fù)雜度為 O(N+K)；

計(jì)數(shù)排序空間復(fù)雜度分析

我們用到了輔助數(shù)組，空間復(fù)雜度為 O（n）

計(jì)數(shù)排序穩(wěn)定性分析

穩(wěn)定性在我們最后存入臨時(shí)數(shù)組時(shí)有體現(xiàn)，我們當(dāng)時(shí)讓其放入臨時(shí)數(shù)組的合適位置，并減一，所以某元素前面的相同元素，在臨時(shí)數(shù)組，仍然在其前面。所以計(jì)數(shù)排序是穩(wěn)定的排序算法。

雖然計(jì)數(shù)排序效率不錯(cuò)但是用到的并不多。

• 這是因?yàn)槠洚?dāng)數(shù)組元素的范圍太大時(shí)，并不適合計(jì)數(shù)排序，不僅浪費(fèi)時(shí)間，效率還會(huì)大大降低。

• 當(dāng)待排序的元素非整數(shù)時(shí),也不適用,大家思考一下這是為什么呢?

好啦,今天的文章就到這啦,我們下期再見(jiàn),拜了個(gè)拜

巨人的肩膀

算法導(dǎo)論

極客時(shí)間數(shù)據(jù)結(jié)構(gòu)與算法之美

https://mp.weixin.qq.com/s/WGqndkwLlzyVOHOdGK7X4Q