計數(shù)排序算法
01
—
計數(shù)排序原理
假設(shè)輸入n個元素,每個元素在區(qū)間0~k內(nèi)的一個整數(shù),區(qū)間k是最大值和最小值之間的區(qū)間。假如輸入元素最大值是5,最小值是2,那么區(qū)間k=5 - 2 + 1 = 4。
計數(shù)排序算法思想:對于每一個輸入元素x,確定小于等于元素x的個數(shù),按照小于等于元素x的個數(shù)確定元素x在輸出序列的索引。當有相同元素時,相同的元素要依次排列。
—
計數(shù)排序?qū)崿F(xiàn)

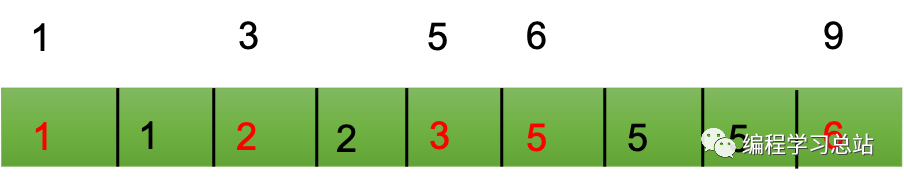
小于元素x的個數(shù)正是元素x在輸出序列中對應(yīng)的索引(索引從0開始),考慮到序列可有相同的元素,同時又要保持Q(n)的時間復(fù)雜度,新建一個k大小的緩沖區(qū),依次保存各個元素對應(yīng)的索引值,如下圖所示。
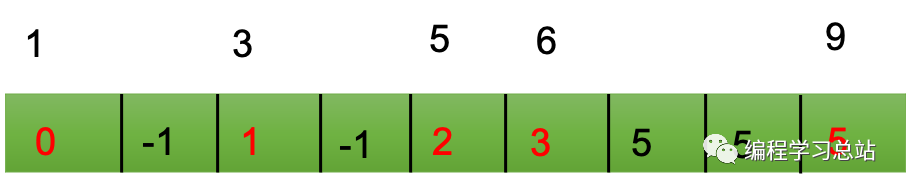
圖中-1的索引表示無效索引,最后遍歷原始序列,按照各個元素的對應(yīng)的索引存放在輸出序列中,相同元素依次排列,對應(yīng)k區(qū)間內(nèi)的保存的索引值加1。最終輸出序列如下圖所示。

計數(shù)排序算法實現(xiàn)代碼如下:
void count_sort(int *input, int input_length, int *output, int output_length){
if(input == NULL || output == NULL || output_length < input_length){
return;
}
int k = 0, max, min;
int i = 0;
min = input[0];
max = input[0];
//找出最大值和最小值
for(i = 0; i < input_length; i++){
if(input[i] < min){
min = input[i];
}
if(input[i] > max){
max = input[i];
}
}
k = max - min + 1; //求出數(shù)值區(qū)間
int *temp = (int *)malloc(sizeof(int) * k);
int *index = (int *)malloc(sizeof(int) * k);
if(temp == NULL){
return;
}
memset(temp, 0, sizeof(int) * k);
memset(index, -1, sizeof(int) * k);
int count = 0;
for(i = 0; i < input_length; i++){
temp[input[i] - min]++; //統(tǒng)計input里每個元素的個數(shù)
}
for(i = 0; i <= k; i++){
count = temp[i];
if(i > 0){
temp[i] = temp[i] + temp[i - 1]; //統(tǒng)計input小于等于各個元素值的個數(shù)
}
if(count > 0){
index[i] = temp[i] - count; //求出各個元素在輸出序列中對應(yīng)的索引值
}
}
for(i = input_length - 1; i >= 0; i--){
output[index[input[i] - min]] = input[i]; //將原始序列中的元素存放在輸出序列對應(yīng)索引中
index[input[i] - min]++; //相同的數(shù)據(jù)相鄰放置
temp[input[i] - min]--;
}
free(temp);
free(index);
}寫一個小程序驗證計數(shù)排序算法的正確性。
#include <stdio.h>
#include "count_sort.h"
#define MAX_LENGTH 10
int main() {
int input[MAX_LENGTH] = {1, 2, -3, 6, 7, 9, 3, 5, 4, 2};
int output[MAX_LENGTH] = {0};
count_sort(input, MAX_LENGTH, output, MAX_LENGTH);
int i = 0;
printf("計數(shù)排序輸出結(jié)果\n");
for(i = 0; i < MAX_LENGTH; i++){
printf("%d ", output[i]);
}
printf("\n");
return 0;
}
編譯運行輸出如下:
計數(shù)排序輸出結(jié)果
-3 1 2 2 3 4 5 6 7 9算法完全正確。
評論
圖片
表情
