Java技術(shù)棧
www.javastack.cn
關(guān)注閱讀更多優(yōu)質(zhì)文章
為什么要有紅黑樹
想必大家對二叉樹搜索樹都不陌生，首先看一下二叉搜索樹的定義：二叉搜索樹（Binary Search Tree），或者是一棵空樹，或者是具有下列性質(zhì)的二叉樹：若它的左子樹不空，則左子樹上所有結(jié)點的值均小于它的根結(jié)點的值；若它的右子樹不空，則右子樹上所有結(jié)點的值均大于它的根結(jié)點的值；它的左、右子樹也分別為二叉排序樹。從理論上來說，二叉搜索樹的查詢、插入和刪除一個節(jié)點的時間復(fù)雜度均為O（log(n)）,已經(jīng)完全可以滿足我們的要求了，那么為什么還要有紅黑樹呢？
我們來看一個例子，向二叉搜索樹中依次插入（1，2，3，4，5，6），插入之后是這樣的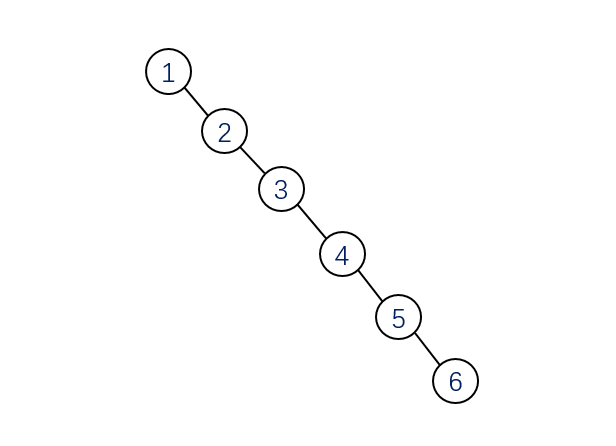
退化成鏈表的二叉搜索樹可以看到，在這種情況下，二叉搜索樹退化成了鏈表！！！這時候查詢、插入和刪除一個元素的時候，時間復(fù)雜度變成了O（n），顯然這是不能接受的。出現(xiàn)這種情況情況的原因是二叉搜索樹沒有自平衡的機制，所以就有了平衡二叉樹的概念。
平衡二叉樹（Balanced Binary Tree）具有以下性質(zhì)：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一棵平衡二叉樹。
還是剛剛的例子，假如我們用平衡二叉樹來實現(xiàn)的話，插入完元素后應(yīng)該是下面這樣的（不唯一）
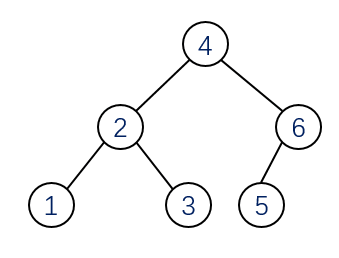自平衡的二叉樹
平衡二叉樹保證了在最差的情況下，二叉樹依然能夠保持絕對的平衡，即左右兩個子樹的高度差的絕對值不超過1。
但是這又會帶來一個問題，那就是平衡二叉樹的定義過于嚴(yán)格，導(dǎo)致每次插入或者刪除一個元素之后，都要去維護二叉樹整體的平衡，這樣產(chǎn)生額外的代價又太大了。
二叉搜索樹可能退化成鏈表，而平衡二叉樹維護平衡的代價開銷又太大了，那怎么辦呢？這就要談到“中庸之道”的智慧了。說白了就是把平衡的定義適當(dāng)放寬，不那么嚴(yán)格，這樣二叉樹既不會退化成鏈表，維護平衡的開銷也可以接受。
沒錯，這就是我們要談的紅黑樹了。首先看一下紅黑樹的定義：
紅黑樹是一種含有紅黑結(jié)點并能自平衡的二叉查找樹。它必須除了滿足二叉搜索樹的性質(zhì)外，還要滿足下面的性質(zhì)：
性質(zhì)1：每個節(jié)點要么是黑色，要么是紅色。
性質(zhì)2：根節(jié)點是黑色。
性質(zhì)3：每個葉子節(jié)點（NIL）是黑色。
性質(zhì)4：每個紅色結(jié)點的兩個子結(jié)點一定都是黑色。
性質(zhì)5：任意一結(jié)點到每個葉子結(jié)點的路徑都包含數(shù)量相同的黑結(jié)點。
這就是紅黑樹的五條性質(zhì)。我相信很多人都看到過，能背下來的也不在少數(shù)，但是真正理解為什么要這樣定義的恐怕就不多了。下面就從2-3樹的角度來談?wù)劶t黑樹的定義。
從2-3樹來看紅黑樹
一般我們接觸最多的是二叉樹，也就是一個父節(jié)點最多有兩個子節(jié)點。2-3樹與二叉樹的不同之處在于，一個父節(jié)點可以有兩個子節(jié)點，也可以有三個子節(jié)點，并且其也滿足類似二叉搜索樹的性質(zhì)。
還有最重要的，2-3樹的所有葉子節(jié)點都在同一層，且最后一層不能有空節(jié)點，類似于滿二叉樹。
我們依次插入10，9，8，7，6，5，4，3，2，1來看一下2-3數(shù)是如何進行自平衡的。
2-3樹在插入元素之前首先要進行一次未命中的查找，然后將元素插入葉子節(jié)點中，之后再進行平衡操作，下面具體說明。
首先插入10，如下圖
2-3樹中插入10
然后插入9，9小于10，2-3樹在插入時要將9融入10這個葉子節(jié)點中（當(dāng)然也是根節(jié)點），融合完成后如下：
2-3樹中插入9
這是一個3節(jié)點，不用執(zhí)行平衡操作。2-3樹中把有兩個元素，三個子節(jié)點的節(jié)點稱為3節(jié)點，把有一個元素，兩個子節(jié)點的的節(jié)點稱為2節(jié)點。接著插入8，插入8的時候同樣要先融入葉子節(jié)點中，如下圖左側(cè)所示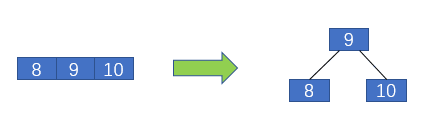
2-3樹中插入8
8融入葉子節(jié)點后，該結(jié)點便擁有了3個元素，不滿足2-3樹的定義，這時就要把3節(jié)點進行分裂，即把左側(cè)和右側(cè)的元素分裂為2節(jié)點，而中間的元素抽出，繼續(xù)融入其父節(jié)點，在這里便成為了一個根節(jié)點。
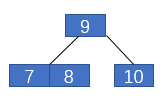2-3樹中插入7
插入后，各個節(jié)點都滿足2-3樹的定義，不需要進行平衡操作。接著插入6，還是首先找到葉子節(jié)點，然后將其融入，如下圖左側(cè)所示
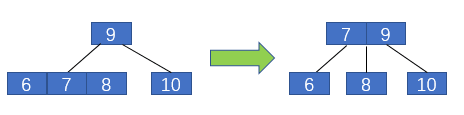2-3樹中插入6
插入后6、7、8三個元素所在的葉子節(jié)點不再滿足2-3樹的定義，需要進行分裂，即抽出元素7融入父節(jié)點，6和8分裂為7的左右子節(jié)點。
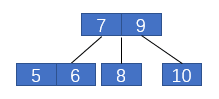2-3樹中插入5
接著插入4，還是首先找到葉子節(jié)點，然后將其融入，如下圖左側(cè)所示
2-3樹中插入4
插入后4、5、6三個元素所在的葉子節(jié)點不再滿足2-3樹的定義，需要進行分裂，即抽出元素5融入父節(jié)點，4和6分裂為5的左右子節(jié)點。5融入父節(jié)點后，該結(jié)點便有了5、7、9三個元素，因而需要繼續(xù)分裂，元素7成為新的根節(jié)點，5和9成為7的左右子節(jié)點。接著插入3，3融入4所在的葉子節(jié)點中，不需要進行平衡操作
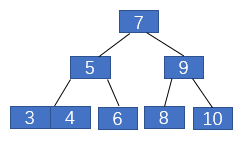2-3樹中插入3
接著插入2，還是首先找到葉子節(jié)點，然后將其融入，如下圖左側(cè)所示
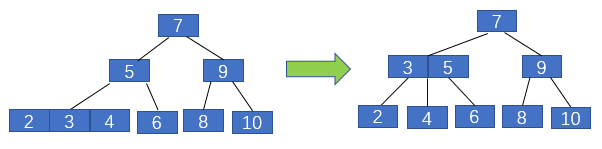2-3樹中插入2
插入后2、3、4三個元素所在的葉子節(jié)點不再滿足2-3樹的定義，需要進行分裂，即抽出元素3融入父節(jié)點，2和4分裂為3的左右子節(jié)點，3融入5所在的父節(jié)點中。最后插入2，同樣先找到葉子節(jié)點，然后將其融入，如下圖所示
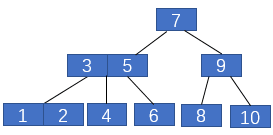2-3樹中插入1
至此，我們便完成了在2-3樹中依次插入10，9，8，7，6，5，4，3，2，1，并且2-3樹始終維護著平衡。怎么樣，是不是很神奇。再看紅黑樹
那么紅黑樹與2-3樹有什么關(guān)系呢？現(xiàn)在我們對2-3樹進行改造，改造成一個二叉樹。怎么改造呢？對于2節(jié)點，保持不變；對于3節(jié)點，我們首先將3節(jié)點中左側(cè)的元素標(biāo)記為紅色，如下圖2所示。
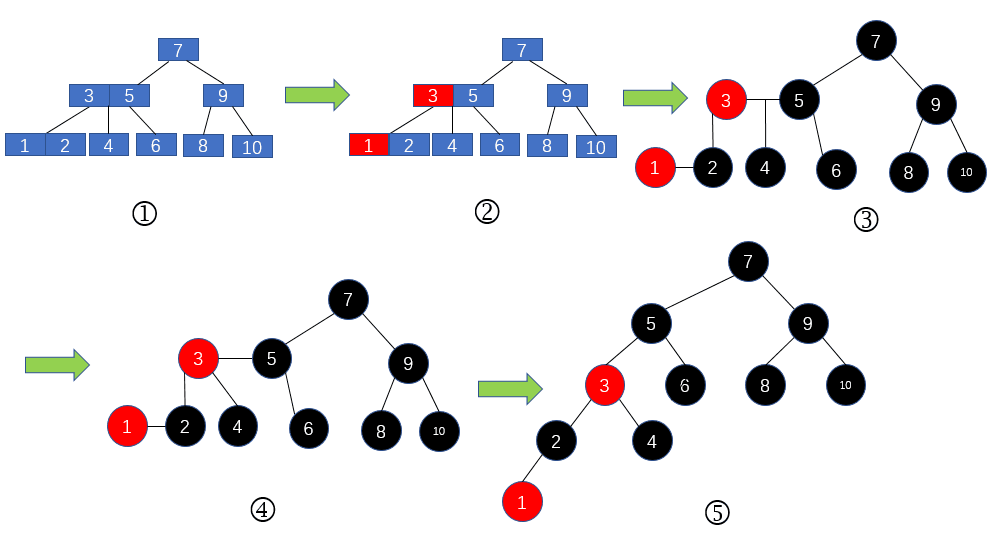2-3樹到紅黑樹的改造
然后我們將其改造成圖3的形式；再將3節(jié)點的位于中間的子節(jié)點的父節(jié)點設(shè)置為父節(jié)點中那個紅色的節(jié)點，如圖4的所示；最后我們將圖4的形式改為二叉樹的樣子，如圖5所示。圖5是不是很熟悉，沒錯，這就是我們常常提到的大名鼎鼎的紅黑樹了。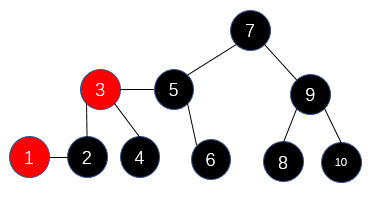
從2-3樹看紅黑樹
性質(zhì)1：每個節(jié)點要么是黑色，要么是紅色。2-3樹中存在2節(jié)點和3節(jié)點，3節(jié)點中左側(cè)的元素便是紅色節(jié)點，而其他的節(jié)點便是黑色節(jié)點。
在2-3樹中，根節(jié)點只能是2節(jié)點或者3節(jié)點，2節(jié)點與3節(jié)點在紅黑樹中的等價形式，如下圖所示
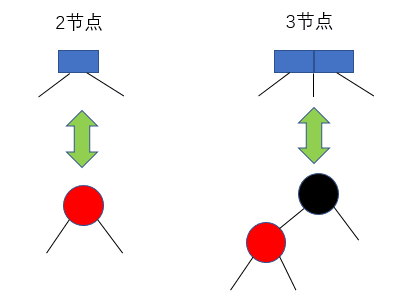2節(jié)點與3節(jié)點在紅黑樹中的等價形式
顯然，無論是哪種情況，根節(jié)點都是黑色的。
性質(zhì)3：每個葉子節(jié)點（NIL）是黑色。這里的葉子節(jié)點不是指左右子樹為空的那個葉子節(jié)點，而是指節(jié)點不存在子節(jié)點或者為空節(jié)點被稱作葉子節(jié)點。在性質(zhì)2中我們討論的根節(jié)點是黑色的都是討論根節(jié)點不為空的情況，若紅黑樹是一個空樹，那么根節(jié)點自然也是空的葉子節(jié)點，這時候葉子節(jié)點便必然是黑色的。
性質(zhì)4：每個紅色結(jié)點的兩個子結(jié)點一定都是黑色。還是從2-3樹的角度來理解，紅色節(jié)點對應(yīng)2-3樹中3節(jié)點左側(cè)的元素，那么它的子節(jié)點要么是2節(jié)點，要么是3節(jié)點。無論是2節(jié)點還是3節(jié)點對應(yīng)的節(jié)點顏色都是黑色的，這在性質(zhì)2時已經(jīng)討論了。
性質(zhì)5：任意一結(jié)點到每個葉子結(jié)點的路徑都包含數(shù)量相同的黑結(jié)點。性質(zhì)5應(yīng)該是紅黑樹最重要的一條性質(zhì)了。2-3樹是一顆絕對平衡的樹，即2-3樹中任意一個節(jié)點出發(fā)，到達(dá)葉子節(jié)點后所經(jīng)過的節(jié)點數(shù)都是一樣的。那么對應(yīng)到紅黑樹呢？2-3樹中2節(jié)點對應(yīng)到紅黑樹便是一個黑色的節(jié)點，而3節(jié)點對應(yīng)到紅黑樹是一個紅色節(jié)點和一個黑色節(jié)點。所以，無論是2節(jié)點還是3節(jié)點，在紅黑樹中都會對應(yīng)一個黑色節(jié)點。那么2-3樹中的絕對平衡，在紅黑樹中自然就是任意一結(jié)點到每個葉子結(jié)點的路徑都包含數(shù)量相同的黑結(jié)點了。
相信大家現(xiàn)在已經(jīng)對紅黑樹的五條性質(zhì)有了更加深刻的體會了。那么我們再看下紅黑樹維持平衡的三種操作，即變色、左旋、右旋怎么理解呢？
首先看一下變色，以下圖為例，
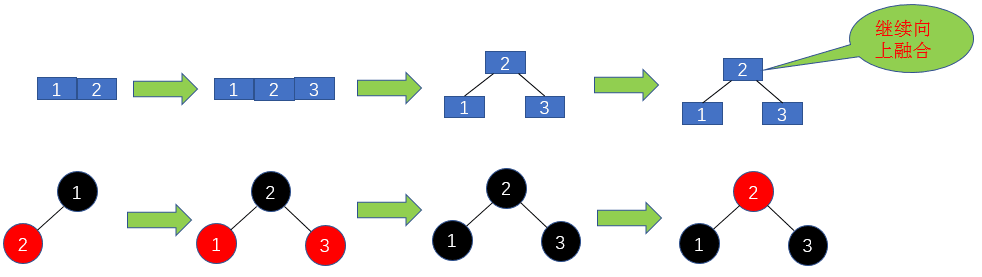紅黑樹的變色
在2-3樹中插入節(jié)點3后，便不再滿足2-3樹的定義，需要進行分解，將元素2抽出作為1和3的父節(jié)點，然后2繼續(xù)向上融合。對應(yīng)到紅黑樹中就是，首先插入節(jié)點3，在紅黑樹中新插入的節(jié)點默認(rèn)為紅色，然后不滿足定義，所以需要進行分解，分解后各個節(jié)點都為2節(jié)點，所以變?yōu)楹谏６?節(jié)點需要繼續(xù)向上融合，故要變成紅色。
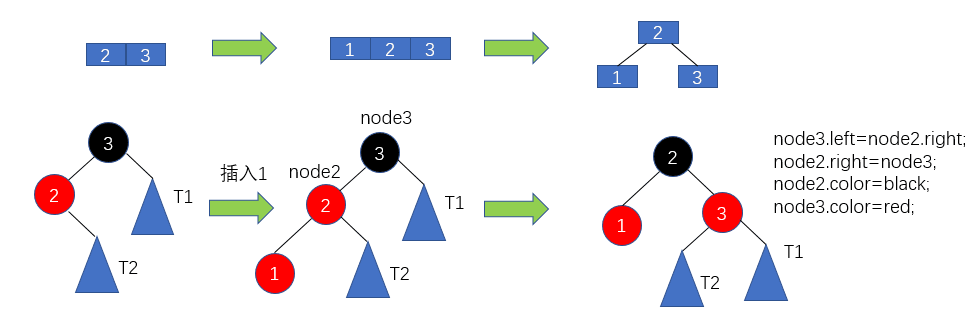紅黑樹的右旋轉(zhuǎn)
插入元素1后，進行右旋轉(zhuǎn)操作，首先把2節(jié)點與3節(jié)點斷開連接，同時把2與2的右子樹斷開連接，然后把2的右子樹連接至3的左子樹位置，不會違背二分搜索樹的性質(zhì)，然后再把3連接至2的右子樹位置。最后還要改變對應(yīng)節(jié)點的顏色，即把2節(jié)點的顏色改為原來3節(jié)點的黑色，把3節(jié)點的顏色改為原來2節(jié)點的紅色。接著看一下左旋轉(zhuǎn)，與右旋轉(zhuǎn)類似，以下圖為例，
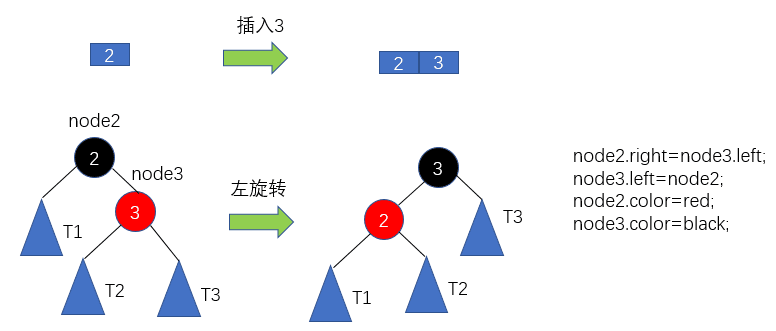紅黑樹的左旋轉(zhuǎn)插入元素3后，進行左旋轉(zhuǎn)操作，首先把2節(jié)點與3節(jié)點斷開連接，同時把3與3的左子樹斷開連接，然后把3的左子樹連接至2的右子樹位置，不會違背二分搜索樹的性質(zhì)，然后再把2連接至3的左子樹位置。最后還要改變對應(yīng)節(jié)點的顏色，即把2節(jié)點的顏色改為原來3節(jié)點的紅色，把3節(jié)點的顏色改為原來2節(jié)點的黑色。寫在最后
最后需要說的是，本文中提到的紅黑樹是一種特殊的紅黑樹——左傾紅黑樹，即紅色節(jié)點都是父節(jié)點的左子樹，其實按照紅黑樹的定義不必這樣。只要滿足紅黑樹的五條性質(zhì)，就是紅黑樹，比如完全可以實現(xiàn)右傾紅黑樹等等，希望大家不要有誤解。
關(guān)注Java技術(shù)棧看更多干貨
