紅黑樹這篇算是將透徹了

先推薦一門算法課程，9.9投資自己不吃虧。

1.紅黑樹簡(jiǎn)介

紅黑樹是一種自平衡的二叉查找樹，是一種高效的查找樹。它是由 Rudolf Bayer 于1978年發(fā)明，在當(dāng)時(shí)被稱為對(duì)稱二叉 B 樹(symmetric binary B-trees)。后來(lái)，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改為如今的紅黑樹。紅黑樹具有良好的效率，它可在?O(logN)?時(shí)間內(nèi)完成查找、增加、刪除等操作。因此，紅黑樹在業(yè)界應(yīng)用很廣泛，比如 Java 中的 TreeMap，JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于紅黑樹結(jié)構(gòu)實(shí)現(xiàn)的。考慮到紅黑樹是一種被廣泛應(yīng)用的數(shù)據(jù)結(jié)構(gòu)，所以我們很有必要去弄懂它。

?2.紅黑樹的性質(zhì)

學(xué)過(guò)二叉查找樹的同學(xué)都知道，普通的二叉查找樹在極端情況下可退化成鏈表，此時(shí)的增刪查效率都會(huì)比較低下。為了避免這種情況，就出現(xiàn)了一些自平衡的查找樹，比如 AVL，紅黑樹等。這些自平衡的查找樹通過(guò)定義一些性質(zhì)，將任意節(jié)點(diǎn)的左右子樹高度差控制在規(guī)定范圍內(nèi)，以達(dá)到平衡狀態(tài)。以紅黑樹為例，紅黑樹通過(guò)如下的性質(zhì)定義實(shí)現(xiàn)自平衡：

1. 節(jié)點(diǎn)是紅色或黑色。

2. 根是黑色。

3. 所有葉子都是黑色（葉子是NIL節(jié)點(diǎn)）。

4. 每個(gè)紅色節(jié)點(diǎn)必須有兩個(gè)黑色的子節(jié)點(diǎn)。（從每個(gè)葉子到根的所有路徑上不能有兩個(gè)連續(xù)的紅色節(jié)點(diǎn)。）

5. 從任一節(jié)點(diǎn)到其每個(gè)葉子的所有簡(jiǎn)單路徑都包含相同數(shù)目的黑色節(jié)點(diǎn)（簡(jiǎn)稱黑高）。

有了上面的幾個(gè)性質(zhì)作為限制，即可避免二叉查找樹退化成單鏈表的情況。但是，僅僅避免這種情況還不夠，這里還要考慮某個(gè)節(jié)點(diǎn)到其每個(gè)葉子節(jié)點(diǎn)路徑長(zhǎng)度的問(wèn)題。如果某些路徑長(zhǎng)度過(guò)長(zhǎng)，那么，在對(duì)這些路徑上的及誒單進(jìn)行增刪查操作時(shí)，效率也會(huì)大大降低。這個(gè)時(shí)候性質(zhì)4和性質(zhì)5用途就凸顯了，有了這兩個(gè)性質(zhì)作為約束，即可保證任意節(jié)點(diǎn)到其每個(gè)葉子節(jié)點(diǎn)路徑最長(zhǎng)不會(huì)超過(guò)最短路徑的2倍。原因如下：

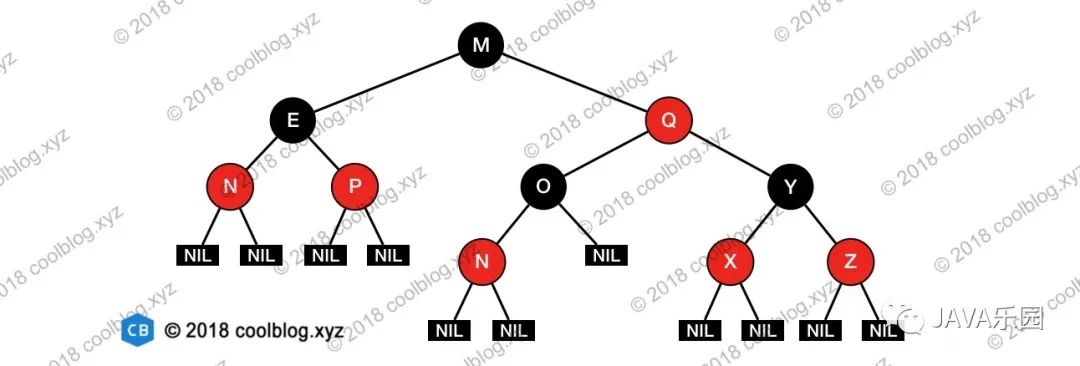
當(dāng)某條路徑最短時(shí)，這條路徑必然都是由黑色節(jié)點(diǎn)構(gòu)成。當(dāng)某條路徑長(zhǎng)度最長(zhǎng)時(shí)，這條路徑必然是由紅色和黑色節(jié)點(diǎn)相間構(gòu)成（性質(zhì)4限定了不能出現(xiàn)兩個(gè)連續(xù)的紅色節(jié)點(diǎn)）。而性質(zhì)5又限定了從任一節(jié)點(diǎn)到其每個(gè)葉子節(jié)點(diǎn)的所有路徑必須包含相同數(shù)量的黑色節(jié)點(diǎn)。此時(shí)，在路徑最長(zhǎng)的情況下，路徑上紅色節(jié)點(diǎn)數(shù)量 = 黑色節(jié)點(diǎn)數(shù)量。該路徑長(zhǎng)度為兩倍黑色節(jié)點(diǎn)數(shù)量，也就是最短路徑長(zhǎng)度的2倍。舉例說(shuō)明一下，請(qǐng)看下圖：

上圖畫出了從根節(jié)點(diǎn) M 出發(fā)的到其葉子節(jié)點(diǎn)的最長(zhǎng)和最短路徑。這里偷懶只畫出了兩條最長(zhǎng)路徑，實(shí)際上最長(zhǎng)路徑有4條，分別為：

M -> Q -> O -> N

M -> Q -> O -> p

M -> Q -> Y -> X

M -> Q -> Y -> Z

長(zhǎng)度為4，最短路徑為?M -> E，長(zhǎng)度為2。最長(zhǎng)路徑的長(zhǎng)度正好為最短路徑長(zhǎng)度的2倍。

前面說(shuō)了關(guān)于紅黑樹的一些性質(zhì)，這里還需要補(bǔ)充一些其他方面的東西。在紅黑樹簡(jiǎn)介一節(jié)中說(shuō)到紅黑樹被發(fā)明出來(lái)的時(shí)候并不叫紅黑樹，而是叫做對(duì)稱二叉 B 樹，從名字中可發(fā)現(xiàn)紅黑樹和 B 樹（這里指的是2-3樹）或許有一定的關(guān)聯(lián)，事實(shí)也正是如此。如果對(duì)紅黑樹的性質(zhì)稍加修改，就能讓紅黑樹和B樹形成一一對(duì)應(yīng)的關(guān)系。關(guān)于紅黑樹和 B 樹關(guān)系的細(xì)節(jié)這里不展開說(shuō)明了，有興趣的同學(xué)可以參考《算法》第4版，那本書上講的很透徹。

?3.紅黑樹操作

紅黑樹的基本操作和其他樹形結(jié)構(gòu)一樣，一般都包括查找、插入、刪除等操作。前面說(shuō)到，紅黑樹是一種自平衡的二叉查找樹，既然是二叉查找樹的一種，那么查找過(guò)程和二叉查找樹一樣，比較簡(jiǎn)單，這里不再贅述。相對(duì)于查找操作，紅黑樹的插入和刪除操作就要復(fù)雜的多。尤其是刪除操作，要處理的情況比較多，不過(guò)大家如果靜下心來(lái)去看，會(huì)發(fā)現(xiàn)其實(shí)也沒想的那么難。好了，廢話就說(shuō)到這，接下來(lái)步入正題吧。

?3.1 旋轉(zhuǎn)操作

在分析插入和刪除操作前，這里需要插個(gè)隊(duì)，先說(shuō)明一下旋轉(zhuǎn)操作，這個(gè)操作在后續(xù)操作中都會(huì)用得到。旋轉(zhuǎn)操作分為左旋和右旋，左旋是將某個(gè)節(jié)點(diǎn)旋轉(zhuǎn)為其右孩子的左孩子，而右旋是節(jié)點(diǎn)旋轉(zhuǎn)為其左孩子的右孩子。這話聽起來(lái)有點(diǎn)繞，所以還是請(qǐng)看下圖：

上圖包含了左旋和右旋的示意圖，這里以右旋為例進(jìn)行說(shuō)明，右旋節(jié)點(diǎn) M 的步驟如下：

1. 將節(jié)點(diǎn) M 的左孩子引用指向節(jié)點(diǎn) E 的右孩子

2. 將節(jié)點(diǎn) E 的右孩子引用指向節(jié)點(diǎn) M，完成旋轉(zhuǎn)

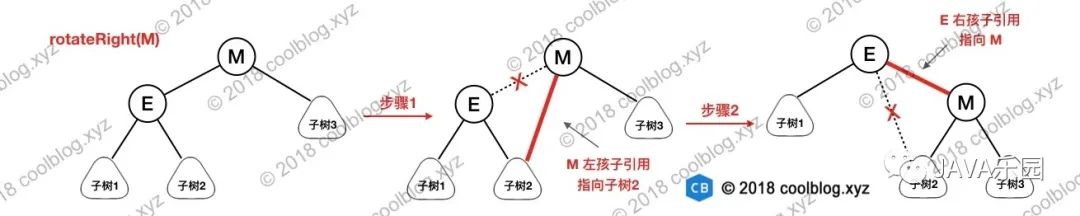
上面分析了右旋操作，左旋操作與此類似，大家有興趣自己畫圖試試吧，這里不再贅述了。旋轉(zhuǎn)操作本身并不復(fù)雜，這里先分析到這吧。

?3.2 插入

紅黑樹的插入過(guò)程和二叉查找樹插入過(guò)程基本類似，不同的地方在于，紅黑樹插入新節(jié)點(diǎn)后，需要進(jìn)行調(diào)整，以滿足紅黑樹的性質(zhì)。性質(zhì)1規(guī)定紅黑樹節(jié)點(diǎn)的顏色要么是紅色要么是黑色，那么在插入新節(jié)點(diǎn)時(shí)，這個(gè)節(jié)點(diǎn)應(yīng)該是紅色還是黑色呢？答案是紅色，原因也不難理解。如果插入的節(jié)點(diǎn)是黑色，那么這個(gè)節(jié)點(diǎn)所在路徑比其他路徑多出一個(gè)黑色節(jié)點(diǎn)，這個(gè)調(diào)整起來(lái)會(huì)比較麻煩（參考紅黑樹的刪除操作，就知道為啥多一個(gè)或少一個(gè)黑色節(jié)點(diǎn)時(shí)，調(diào)整起來(lái)這么麻煩了）。如果插入的節(jié)點(diǎn)是紅色，此時(shí)所有路徑上的黑色節(jié)點(diǎn)數(shù)量不變，僅可能會(huì)出現(xiàn)兩個(gè)連續(xù)的紅色節(jié)點(diǎn)的情況。這種情況下，通過(guò)變色和旋轉(zhuǎn)進(jìn)行調(diào)整即可，比之前的簡(jiǎn)單多了。

接下來(lái)，將分析插入紅色節(jié)點(diǎn)后紅黑樹的情況。這里假設(shè)要插入的節(jié)點(diǎn)為 N，N 的父節(jié)點(diǎn)為 P，祖父節(jié)點(diǎn)為 G，叔叔節(jié)點(diǎn)為 U。插入紅色節(jié)點(diǎn)后，會(huì)出現(xiàn)5種情況，分別如下：

?3.2.1 情況一

插入的新節(jié)點(diǎn) N 是紅黑樹的根節(jié)點(diǎn)，這種情況下，我們把節(jié)點(diǎn) N 的顏色由紅色變?yōu)楹谏再|(zhì)2（根是黑色）被滿足。同時(shí) N 被染成黑色后，紅黑樹所有路徑上的黑色節(jié)點(diǎn)數(shù)量增加一個(gè)，性質(zhì)5（從任一節(jié)點(diǎn)到其每個(gè)葉子的所有簡(jiǎn)單路徑都包含相同數(shù)目的黑色節(jié)點(diǎn)）仍然被滿足。

?3.2.2 情況二

N 的父節(jié)點(diǎn)是黑色，這種情況下，性質(zhì)4（每個(gè)紅色節(jié)點(diǎn)必須有兩個(gè)黑色的子節(jié)點(diǎn)）和性質(zhì)5沒有受到影響，不需要調(diào)整。

?3.2.3 情況三

N 的父節(jié)點(diǎn)是紅色（節(jié)點(diǎn) P 為紅色，其父節(jié)點(diǎn)必然為黑色），叔叔節(jié)點(diǎn) U 也是紅色。由于 P 和 N 均為紅色，所有性質(zhì)4被打破，此時(shí)需要進(jìn)行調(diào)整。這種情況下，先將 P 和 U 的顏色染成黑色，再將 G 的顏色染成紅色。此時(shí)經(jīng)過(guò) G 的路徑上的黑色節(jié)點(diǎn)數(shù)量不變，性質(zhì)5仍然滿足。但需要注意的是 G 被染成紅色后，可能會(huì)和它的父節(jié)點(diǎn)形成連續(xù)的紅色節(jié)點(diǎn)，此時(shí)需要遞歸向上調(diào)整。

?3.2.4 情況四

N 的父節(jié)點(diǎn)為紅色，叔叔節(jié)點(diǎn)為黑色。節(jié)點(diǎn) N 是 P 的右孩子，且節(jié)點(diǎn) P 是 G 的左孩子。此時(shí)先對(duì)節(jié)點(diǎn) P 進(jìn)行左旋，調(diào)整 N 與 P 的位置。接下來(lái)按照情況五進(jìn)行處理，以恢復(fù)性質(zhì)4。

?3.2.5 情況五

N 的父節(jié)點(diǎn)為紅色，叔叔節(jié)點(diǎn)為黑色。N 是 P 的左孩子，且節(jié)點(diǎn) P 是 G 的左孩子。此時(shí)對(duì) G 進(jìn)行右旋，調(diào)整 P 和 G 的位置，并互換顏色。經(jīng)過(guò)這樣的調(diào)整后，性質(zhì)4被恢復(fù)，同時(shí)也未破壞性質(zhì)5。

?3.2.6 插入總結(jié)

上面五種情況中，情況一和情況二比較簡(jiǎn)單，情況三、四、五稍復(fù)雜。但如果細(xì)心觀察，會(huì)發(fā)現(xiàn)這三種情況的區(qū)別在于叔叔節(jié)點(diǎn)的顏色，如果叔叔節(jié)點(diǎn)為紅色，直接變色即可。如果叔叔節(jié)點(diǎn)為黑色，則需要選選擇，再交換顏色。當(dāng)把這三種情況的圖畫在一起就區(qū)別就比較容易觀察了，如下圖：

?3.3 刪除

相較于插入操作，紅黑樹的刪除操作則要更為復(fù)雜一些。刪除操作首先要確定待刪除節(jié)點(diǎn)有幾個(gè)孩子，如果有兩個(gè)孩子，不能直接刪除該節(jié)點(diǎn)。而是要先找到該節(jié)點(diǎn)的前驅(qū)（該節(jié)點(diǎn)左子樹中最大的節(jié)點(diǎn)）或者后繼（該節(jié)點(diǎn)右子樹中最小的節(jié)點(diǎn)），然后將前驅(qū)或者后繼的值復(fù)制到要?jiǎng)h除的節(jié)點(diǎn)中，最后再將前驅(qū)或后繼刪除。由于前驅(qū)和后繼至多只有一個(gè)孩子節(jié)點(diǎn)，這樣我們就把原來(lái)要?jiǎng)h除的節(jié)點(diǎn)有兩個(gè)孩子的問(wèn)題轉(zhuǎn)化為只有一個(gè)孩子節(jié)點(diǎn)的問(wèn)題，問(wèn)題被簡(jiǎn)化了一些。我們并不關(guān)心最終被刪除的節(jié)點(diǎn)是否是我們開始想要?jiǎng)h除的那個(gè)節(jié)點(diǎn)，只要節(jié)點(diǎn)里的值最終被刪除就行了，至于樹結(jié)構(gòu)如何變化，這個(gè)并不重要。

紅黑樹刪除操作的復(fù)雜度在于刪除節(jié)點(diǎn)的顏色，當(dāng)刪除的節(jié)點(diǎn)是紅色時(shí)，直接拿其孩子節(jié)點(diǎn)補(bǔ)空位即可。因?yàn)閯h除紅色節(jié)點(diǎn)，性質(zhì)5（從任一節(jié)點(diǎn)到其每個(gè)葉子的所有簡(jiǎn)單路徑都包含相同數(shù)目的黑色節(jié)點(diǎn)）仍能夠被滿足。當(dāng)刪除的節(jié)點(diǎn)是黑色時(shí)，那么所有經(jīng)過(guò)該節(jié)點(diǎn)的路徑上的黑節(jié)點(diǎn)數(shù)量少了一個(gè)，破壞了性質(zhì)5。如果該節(jié)點(diǎn)的孩子為紅色，直接拿孩子節(jié)點(diǎn)替換被刪除的節(jié)點(diǎn)，并將孩子節(jié)點(diǎn)染成黑色，即可恢復(fù)性質(zhì)5。但如果孩子節(jié)點(diǎn)為黑色，處理起來(lái)就要復(fù)雜的多。分為6種情況，下面會(huì)展開說(shuō)明。

在展開說(shuō)明之前，我們先做一些假設(shè)，方便說(shuō)明。這里假設(shè)最終被刪除的節(jié)點(diǎn)為X（至多只有一個(gè)孩子節(jié)點(diǎn)），其孩子節(jié)點(diǎn)為N，X的兄弟節(jié)點(diǎn)為S，S的左節(jié)點(diǎn)為 SL，右節(jié)點(diǎn)為 SR。接下來(lái)討論是建立在節(jié)點(diǎn)?X?被刪除，節(jié)點(diǎn)?N?替換X的基礎(chǔ)上進(jìn)行的。這里說(shuō)明把被刪除的節(jié)點(diǎn)X特地拎出來(lái)說(shuō)一下的原因是防止大家誤以為節(jié)點(diǎn)N會(huì)被刪除，不然后面就會(huì)看不明白。

在上面的基礎(chǔ)上，接下來(lái)就可以展開討論了。紅黑樹刪除有6種情況，分別是：

?3.3.1 情況一

N 是新的根。在這種情形下，我們就做完了。我們從所有路徑去除了一個(gè)黑色節(jié)點(diǎn)，而新根是黑色的，所以性質(zhì)都保持著。

上面是維基百科中關(guān)于紅黑樹刪除的情況一說(shuō)明，由于沒有配圖，看的有點(diǎn)暈。經(jīng)過(guò)思考，我覺得可能會(huì)是下面這種情形：

要?jiǎng)h除的節(jié)點(diǎn) X 是根節(jié)點(diǎn)，且左右孩子節(jié)點(diǎn)均為空節(jié)點(diǎn)，此時(shí)將節(jié)點(diǎn) X 用空節(jié)點(diǎn)替換完成刪除操作。

可能還有其他情形，大家如果知道，煩請(qǐng)告知。

?3.3.2 情況二

S 為紅色，其他節(jié)點(diǎn)為黑色。這種情況下可以對(duì) N 的父節(jié)點(diǎn)進(jìn)行左旋操作，然后互換 P 與 S 顏色。但這并未結(jié)束，經(jīng)過(guò)節(jié)點(diǎn) P 和 N 的路徑刪除前有3個(gè)黑色節(jié)點(diǎn)（P -> X -> N），現(xiàn)在只剩兩個(gè)了（P -> N）。比未經(jīng)過(guò) N 的路徑少一個(gè)黑色節(jié)點(diǎn)，性質(zhì)5仍不滿足，還需要繼續(xù)調(diào)整。不過(guò)此時(shí)可以按照情況四、五、六進(jìn)行調(diào)整。

?3.3.2 情況三

N 的父節(jié)點(diǎn)，兄弟節(jié)點(diǎn) S 和 S 的孩子節(jié)點(diǎn)均為黑色。這種情況下可以簡(jiǎn)單的把 S 染成紅色，所有經(jīng)過(guò) S 的路徑比之前少了一個(gè)黑色節(jié)點(diǎn)，這樣經(jīng)過(guò) N 的路徑和經(jīng)過(guò) S 的路徑黑色節(jié)點(diǎn)數(shù)量一致了。但經(jīng)過(guò) P 的路徑比不經(jīng)過(guò) P 的路徑少一個(gè)黑色節(jié)點(diǎn)，此時(shí)需要從情況一開始對(duì) P 進(jìn)行平衡處理。

?3.3.4 情況四

N 的父節(jié)點(diǎn)為紅色，叔叔節(jié)點(diǎn)為黑色。節(jié)點(diǎn) N 是 P 的右孩子，且節(jié)點(diǎn) P 是 G 的左孩子。此時(shí)先對(duì)節(jié)點(diǎn) P 進(jìn)行左旋，調(diào)整 N 與 P 的位置。接下來(lái)按照情況五進(jìn)行處理，以恢復(fù)性質(zhì)4。

這里需要特別說(shuō)明一下，上圖中的節(jié)點(diǎn) N 并非是新插入的節(jié)點(diǎn)。當(dāng) P 為紅色時(shí)，P 有兩個(gè)孩子節(jié)點(diǎn)，且孩子節(jié)點(diǎn)均為黑色，這樣從 G 出發(fā)到各葉子節(jié)點(diǎn)路徑上的黑色節(jié)點(diǎn)數(shù)量才能保持一致。既然 P 已經(jīng)有兩個(gè)孩子了，所以 N 不是新插入的節(jié)點(diǎn)。情況四是由以 N 為根節(jié)點(diǎn)的子樹中插入了新節(jié)點(diǎn)，經(jīng)過(guò)調(diào)整后，導(dǎo)致 N 被變?yōu)榧t色，進(jìn)而導(dǎo)致了情況四的出現(xiàn)。考慮下面這種情況（PR?節(jié)點(diǎn)就是上圖的 N 節(jié)點(diǎn)）：

如上圖，插入節(jié)點(diǎn) N 并按情況三處理。此時(shí) PR?被染成了紅色，與 P 節(jié)點(diǎn)形成了連續(xù)的紅色節(jié)點(diǎn)，這個(gè)時(shí)候就需按情況四再次進(jìn)行調(diào)整。

?3.3.5 情況五

S 為黑色，S 的左孩子為紅色，右孩子為黑色。N 的父節(jié)點(diǎn)顏色可紅可黑，且 N 是 P 左孩子。這種情況下對(duì) S 進(jìn)行右旋操作，并互換 S 和 SL?的顏色。此時(shí)，所有路徑上的黑色數(shù)量仍然相等，N 兄弟節(jié)點(diǎn)的由 S 變?yōu)榱?SL，而 SL?的右孩子變?yōu)榧t色。接下來(lái)我們到情況六繼續(xù)分析。

?3.3.6 情況六

S 為黑色，S 的右孩子為紅色。N 的父節(jié)點(diǎn)顏色可紅可黑，且 N 是其父節(jié)點(diǎn)左孩子。這種情況下，我們對(duì) P 進(jìn)行左旋操作，并互換 P 和 S 的顏色，并將 SR?變?yōu)楹谏Ｒ驗(yàn)?P 變?yōu)楹谏越?jīng)過(guò) N 的路徑多了一個(gè)黑色節(jié)點(diǎn)，經(jīng)過(guò) N 的路徑上的黑色節(jié)點(diǎn)與刪除前的數(shù)量一致。對(duì)于不經(jīng)過(guò) N 的路徑，則有以下兩種情況：

1. 該路徑經(jīng)過(guò) N 新的兄弟節(jié)點(diǎn) SL?，那它之前必然經(jīng)過(guò) S 和 P。而 S 和 P 現(xiàn)在只是交換顏色，對(duì)于經(jīng)過(guò) SL?的路徑不影響。

2. 該路徑經(jīng)過(guò) N 新的叔叔節(jié)點(diǎn) SR，那它之前必然經(jīng)過(guò) P、 S 和 SR，而現(xiàn)在它只經(jīng)過(guò) S 和 SR。在對(duì) P 進(jìn)行左旋，并與 S 換色后，經(jīng)過(guò) SR?的路徑少了一個(gè)黑色節(jié)點(diǎn)，性質(zhì)5被打破。另外，由于 S 的顏色可紅可黑，如果 S 是紅色的話，會(huì)與 SR?形成連續(xù)的紅色節(jié)點(diǎn)，打破性質(zhì)4（每個(gè)紅色節(jié)點(diǎn)必須有兩個(gè)黑色的子節(jié)點(diǎn)）。此時(shí)僅需將 SR?由紅色變?yōu)楹谏纯赏瑫r(shí)恢復(fù)性質(zhì)4和性質(zhì)5（從任一節(jié)點(diǎn)到其每個(gè)葉子的所有簡(jiǎn)單路徑都包含相同數(shù)目的黑色節(jié)點(diǎn)。）。

?3.3.7 刪除總結(jié)

紅黑樹刪除的情況比較多，大家剛開始看的時(shí)候可能會(huì)比較暈。可能會(huì)產(chǎn)生這樣的疑問(wèn)，為啥紅黑樹會(huì)有這種刪除情況，為啥又會(huì)有另一種情況，它們之間有什么聯(lián)系和區(qū)別？和大家一樣，我剛開始看的時(shí)候也有這樣的困惑，直到我把所有情況對(duì)應(yīng)的圖形畫在一起時(shí)，撥云見日，一切都明了了。此時(shí)天空中出現(xiàn)了4個(gè)字，原來(lái)如此、原來(lái)如此、原來(lái)如此。所以，請(qǐng)看圖吧：

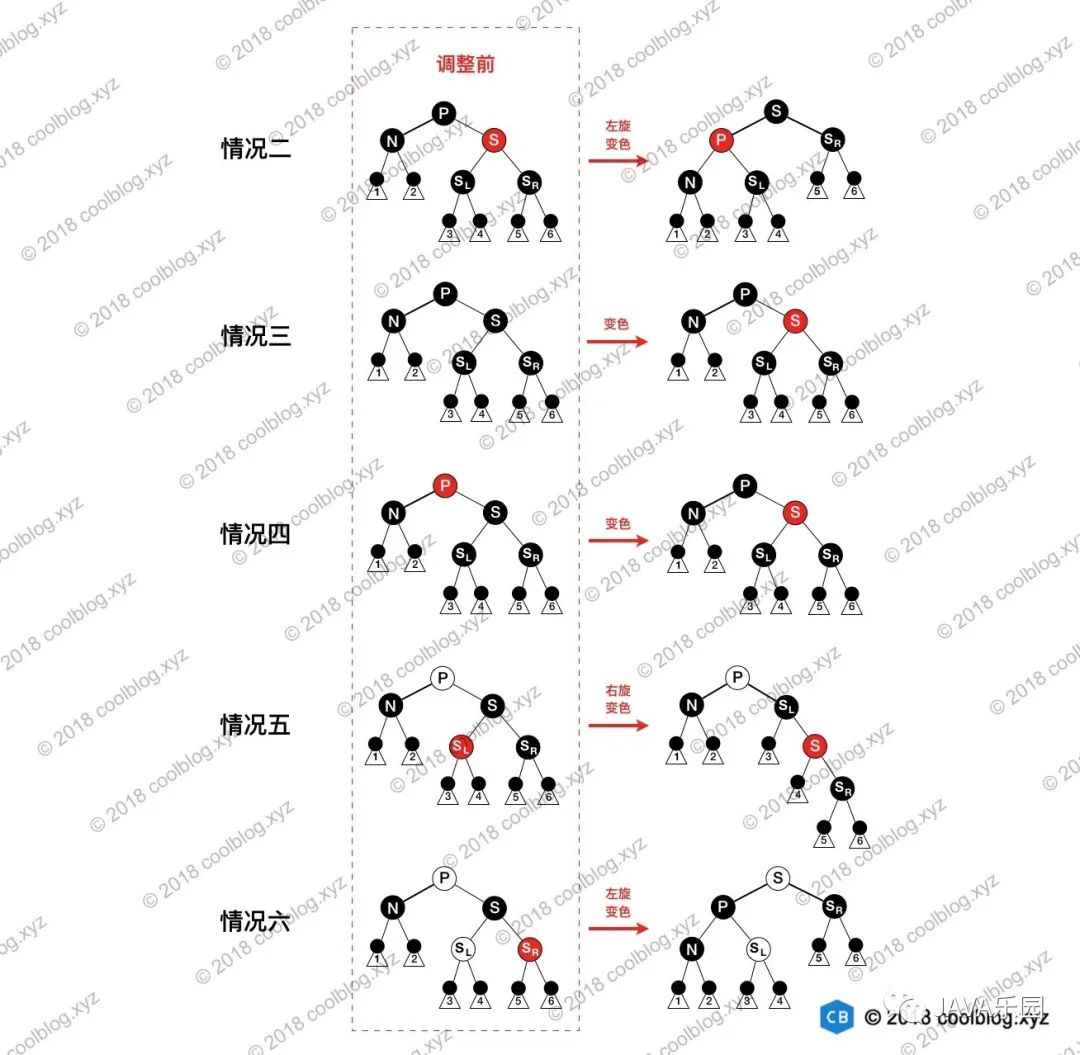
?4.總結(jié)

紅黑樹是一種重要的二叉樹，應(yīng)用廣泛，但在很多數(shù)據(jù)結(jié)構(gòu)相關(guān)的書本中出現(xiàn)的次數(shù)并不多。很多書中要么不說(shuō)，要么就一筆帶過(guò)，并不會(huì)進(jìn)行詳細(xì)的分析，這可能是因?yàn)榧t黑樹比較復(fù)雜的緣故。我在學(xué)習(xí)紅黑樹的時(shí)候也找了很多資料，但總體感覺講的都不太好。尤其是在我學(xué)習(xí)刪除操作的時(shí)候，很多資料是實(shí)在人看不下去，看的我很痛苦。直到我看到維基百科上關(guān)于紅黑樹的分析時(shí)，很是欣喜。這篇文章分析的很有條理，言簡(jiǎn)意賅，比很多資料好了太多。本文對(duì)紅黑樹的分析也主要參考了維基百科中的紅黑樹分析，并對(duì)維基百科中容易讓人產(chǎn)生疑問(wèn)和誤解的地方進(jìn)行了說(shuō)明。同時(shí)維基百科中文版紅黑樹文中的圖片較為模糊，這里我重新進(jìn)行了繪制。需要說(shuō)明的是，維基百科中文版無(wú)法打開了，文中關(guān)于維基百科的鏈接都是英文版的。另外在給大家推薦一個(gè)數(shù)據(jù)結(jié)構(gòu)可視化的網(wǎng)站，里面包含常見數(shù)據(jù)結(jié)構(gòu)可視化過(guò)程，地址為：t.cn/RZFgryr。

另外，由于紅黑樹本身比較復(fù)雜，實(shí)現(xiàn)也較為復(fù)雜。在寫這篇文章之前，我曾嘗試過(guò)用 Java 語(yǔ)言實(shí)現(xiàn)紅黑樹的增刪操作，最終只寫出了新增節(jié)點(diǎn)操作，刪除沒做出來(lái)。而且自己寫的新增邏輯實(shí)在太繁瑣，寫的不好看，沒法拿出來(lái) show。所以最后把 Java 中的 TreeMap 增刪相關(guān)源碼拷出來(lái)，按照自己的需求把源碼修改了一下，也勉強(qiáng)算是實(shí)現(xiàn)了紅黑樹吧。代碼放到了 github 上，傳送門 -> RBTree.java。

最后，如果你也在學(xué)習(xí)紅黑樹，希望這篇文章能夠幫助到你。另外，由于紅黑樹本身比較復(fù)雜，加之本人水平有限，難免會(huì)出一些錯(cuò)誤。如果有錯(cuò)，還望大家指出來(lái)，我們共同討論。

source:?http://www.tianxiaobo.com/2018/01/11/紅黑樹詳細(xì)分析/

關(guān)注我

每天進(jìn)步一點(diǎn)點(diǎn)