一文看盡深度學(xué)習(xí)中的15種損失函數(shù)

在機(jī)器學(xué)習(xí)中，損失函數(shù)是代價(jià)函數(shù)的一部分，而代價(jià)函數(shù)則是目標(biāo)函數(shù)的一種類型[1]。

Loss function，即損失函數(shù)：用于定義單個(gè)訓(xùn)練樣本與真實(shí)值之間的誤差；

Cost function，即代價(jià)函數(shù)：用于定義單個(gè)批次/整個(gè)訓(xùn)練集樣本與真實(shí)值之間的誤差；

Objective function，即目標(biāo)函數(shù)：泛指任意可以被優(yōu)化的函數(shù)。

損失函數(shù)是用于衡量模型所作出的預(yù)測離真實(shí)值（Ground Truth）之間的偏離程度。通常，我們都會(huì)最小化目標(biāo)函數(shù)，最常用的算法便是“梯度下降法”（Gradient Descent）。俗話說，任何事情必然有它的兩面性，因此，并沒有一種萬能的損失函數(shù)能夠適用于所有的機(jī)器學(xué)習(xí)任務(wù)，所以在這里我們需要知道每一種損失函數(shù)的優(yōu)點(diǎn)和局限性，才能更好的利用它們?nèi)ソ鉀Q實(shí)際的問題。損失函數(shù)大致可分為兩種：回歸損失（針對連續(xù)型變量）和分類損失（針對離散型變量）。

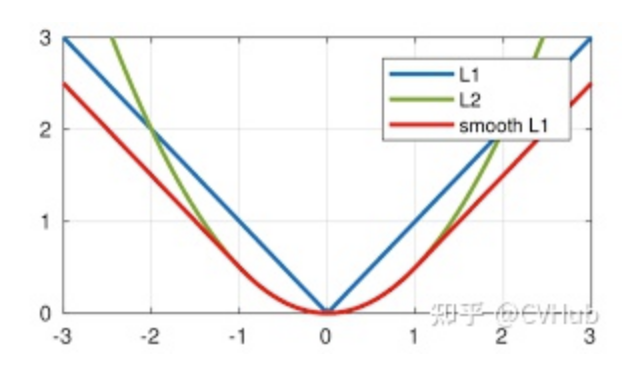
1. 回歸損失（Regression Loss）

• L1 Loss

也稱為Mean Absolute Error，即平均絕對誤差（MAE），它衡量的是預(yù)測值與真實(shí)值之間距離的平均誤差幅度，作用范圍為0到正無窮。

優(yōu)點(diǎn)： 收斂速度快，能夠?qū)μ荻冉o予合適的懲罰權(quán)重，而不是“一視同仁”，使梯度更新的方向可以更加精確。

缺點(diǎn)： 對異常值十分敏感，梯度更新的方向很容易受離群點(diǎn)所主導(dǎo)，不具備魯棒性。

• L2 Loss

也稱為Mean Squred Error，即均方差（MSE），它衡量的是預(yù)測值與真實(shí)1值之間距離的平方和，作用范圍同為0到正無窮。

優(yōu)點(diǎn)： 對離群點(diǎn)（Outliers）或者異常值更具有魯棒性。

缺點(diǎn)： 由圖可知其在0點(diǎn)處的導(dǎo)數(shù)不連續(xù)，使得求解效率低下，導(dǎo)致收斂速度慢；而對于較小的損失值，其梯度也同其他區(qū)間損失值的梯度一樣大，所以不利于網(wǎng)絡(luò)的學(xué)習(xí)。

對于L1范數(shù)和L2范數(shù)，如果異常值對于實(shí)際業(yè)務(wù)非常重要，我們可以使用MSE作為我們的損失函數(shù)；另一方面，如果異常值僅僅表示損壞的數(shù)據(jù)，那我們應(yīng)該選擇MAE作為損失函數(shù)。此外，考慮到收斂速度，在大多數(shù)的卷積神經(jīng)網(wǎng)絡(luò)中（CNN）中，我們通常會(huì)選擇L2損失。但是，還存在這樣一種情形，當(dāng)你的業(yè)務(wù)數(shù)據(jù)中，存在95%的數(shù)據(jù)其真實(shí)值為1000，而剩下5%的數(shù)據(jù)其真實(shí)值為10時(shí)，如果你使用MAE去訓(xùn)練模型，則訓(xùn)練出來的模型會(huì)偏向于將所有輸入數(shù)據(jù)預(yù)測成1000，因?yàn)镸AE對離群點(diǎn)不敏感，趨向于取中值。而采用MSE去訓(xùn)練模型時(shí)，訓(xùn)練出來的模型會(huì)偏向于將大多數(shù)的輸入數(shù)據(jù)預(yù)測成10，因?yàn)樗鼘﹄x群點(diǎn)異常敏感。因此，大多數(shù)情況這兩種回歸損失函數(shù)并不適用，能否有什么辦法可以同時(shí)利用這兩者的優(yōu)點(diǎn)呢？

• Smooth L1 Loss

即平滑的L1損失（SLL），出自Fast RCNN [7]。SLL通過綜合L1和L2損失的優(yōu)點(diǎn)，在0點(diǎn)處附近采用了L2損失中的平方函數(shù)，解決了L1損失在0點(diǎn)處梯度不可導(dǎo)的問題，使其更加平滑易于收斂。此外，在|x|>1的區(qū)間上，它又采用了L1損失中的線性函數(shù)，使得梯度能夠快速下降。

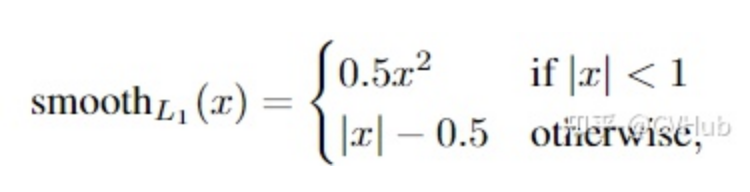
通過對這三個(gè)損失函數(shù)進(jìn)行求導(dǎo)可以發(fā)現(xiàn)，L1損失的導(dǎo)數(shù)為常數(shù)，如果不及時(shí)調(diào)整學(xué)習(xí)率，那么當(dāng)值過小時(shí)，會(huì)導(dǎo)致模型很難收斂到一個(gè)較高的精度，而是趨向于一個(gè)固定值附近波動(dòng)。反過來，對于L2損失來說，由于在訓(xùn)練初期值較大時(shí)，其導(dǎo)數(shù)值也會(huì)相應(yīng)較大，導(dǎo)致訓(xùn)練不穩(wěn)定。最后，可以發(fā)現(xiàn)Smooth L1在訓(xùn)練初期輸入數(shù)值較大時(shí)能夠較為穩(wěn)定在某一個(gè)數(shù)值，而在后期趨向于收斂時(shí)也能夠加速梯度的回傳，很好的解決了前面兩者所存在的問題。

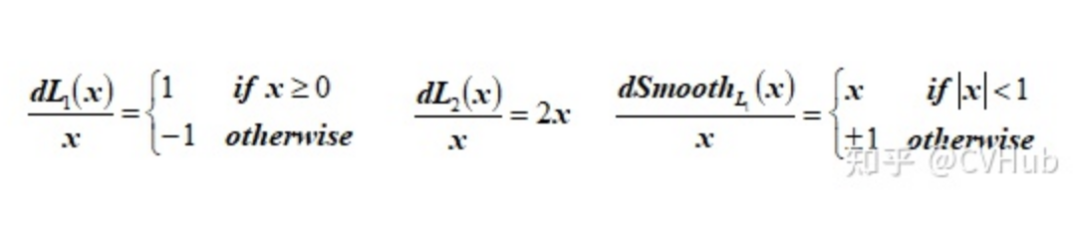
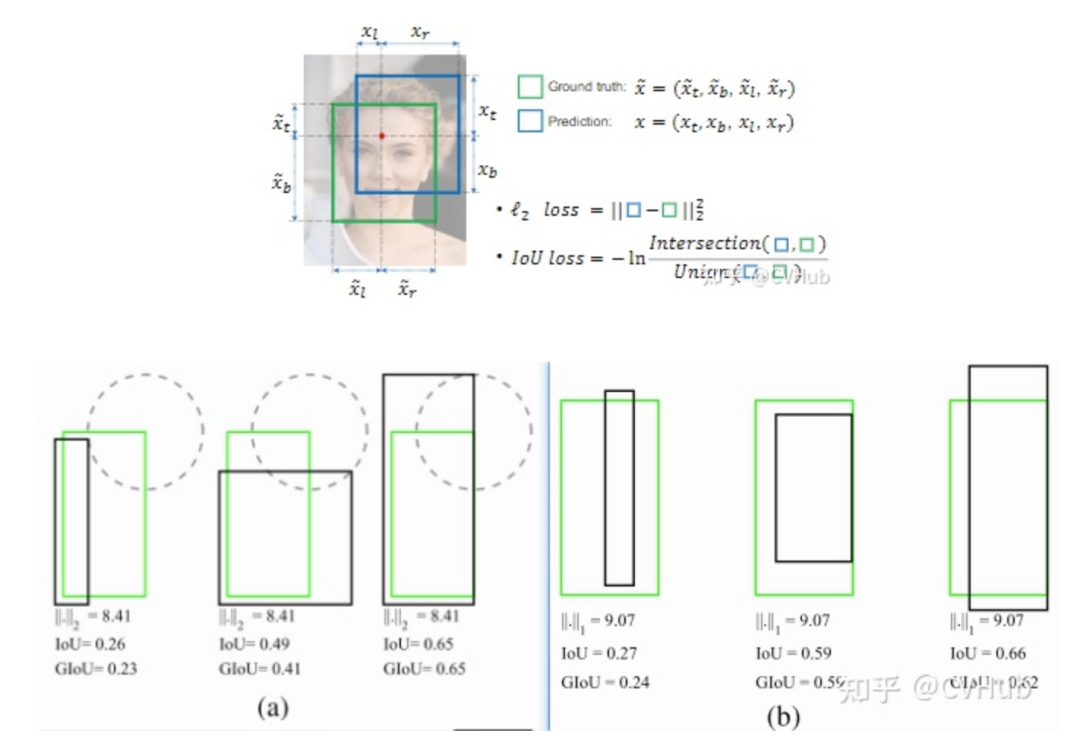
• IoU Loss

即交并比損失，出自UnitBox [8]，由曠視科技于ACM2016首次提出。常規(guī)的Lx損失中，都是基于目標(biāo)邊界中的4個(gè)坐標(biāo)點(diǎn)信息之間分別進(jìn)行回歸損失計(jì)算的。因此，這些邊框信息之間是相互獨(dú)立的。然而，直觀上來看，這些邊框信息之間必然是存在某種相關(guān)性的。如下圖(a)-(b)分別所示，綠色框代表Ground Truth，黑色框代表Prediction，可以看出，同一個(gè)Lx分?jǐn)?shù)，預(yù)測框與真實(shí)框之間的擬合/重疊程度并不相同，顯然重疊度越高的預(yù)測框是越合理的。IoU損失將候選框的四個(gè)邊界信息作為一個(gè)整體進(jìn)行回歸，從而實(shí)現(xiàn)準(zhǔn)確、高效的定位，具有很好的尺度不變性。為了解決IoU度量不可導(dǎo)的現(xiàn)象，引入了負(fù)Ln范數(shù)來間接計(jì)算IoU損失。

• GIoU Loss

即泛化的IoU損失，全稱為Generalized Intersection over Union，由斯坦福學(xué)者于CVPR2019年發(fā)表的這篇論文（https://arxiv.org/abs/1902.09630） [9]中首次提出。上面我們提到了IoU損失可以解決邊界框坐標(biāo)之間相互獨(dú)立的問題，考慮這樣一種情況，當(dāng)預(yù)測框與真實(shí)框之間沒有任何重疊時(shí)，兩個(gè)邊框的交集（分子）為0，此時(shí)IoU損失為0，因此IoU無法算出兩者之間的距離（重疊度）。另一方面，由于IoU損失為零，意味著梯度無法有效地反向傳播和更新，即出現(xiàn)梯度消失的現(xiàn)象，致使網(wǎng)絡(luò)無法給出一個(gè)優(yōu)化的方向。此外，如下圖所示，IoU對不同方向的邊框?qū)R也是一臉懵逼的，所計(jì)算出來的值都一樣。

為了解決以上的問題，如下圖公式所示，GIoU通過計(jì)算任意兩個(gè)形狀（這里以矩形框?yàn)槔〢和B的一個(gè)最小閉合凸面C，然后再計(jì)算C中排除掉A和B后的面積占C原始面積的比值，最后再用原始的IoU減去這個(gè)比值得到泛化后的IoU值。

GIoU具有IoU所擁有的一切特性，如對稱性，三角不等式等。GIoU ≤ IoU，特別地，0 ≤ IoU(A, B) ≤ -1, 而0 ≤ GIoU(A, B) ≤ -1；當(dāng)兩個(gè)邊框的完全重疊時(shí)，此時(shí)GIoU = IoU = 1. 而當(dāng) |AUB| 與 最小閉合凸面C 的比值趨近為0時(shí)，即兩個(gè)邊框不相交的情況下，此時(shí)GIoU將漸漸收斂至 -1. 同樣地，我們也可以通過一定的方式去計(jì)算出兩個(gè)矩形框之間的GIoU損失，具體計(jì)算步驟也非常簡單，詳情參考原論文。

• DIoU Loss

即距離IoU損失，全稱為Distance-IoU loss，由天津大學(xué)數(shù)學(xué)學(xué)院研究人員于AAAI2020所發(fā)表的這篇論文 （https://arxiv.org/abs/1911.08287）中首次提出。上面我們談到GIoU通過引入最小閉合凸面來解決IoU無法對不重疊邊框的優(yōu)化問題。但是，其仍然存在兩大局限性：邊框回歸還不夠精確 & 收斂速度緩慢 。考慮下圖這種情況，當(dāng)目標(biāo)框完全包含預(yù)測框時(shí)，此時(shí)GIoU退化為IoU。顯然，我們希望的預(yù)測是最右邊這種情況。因此，作者通過計(jì)算兩個(gè)邊框之間的中心點(diǎn)歸一化距離，從而更好的優(yōu)化這種情況。

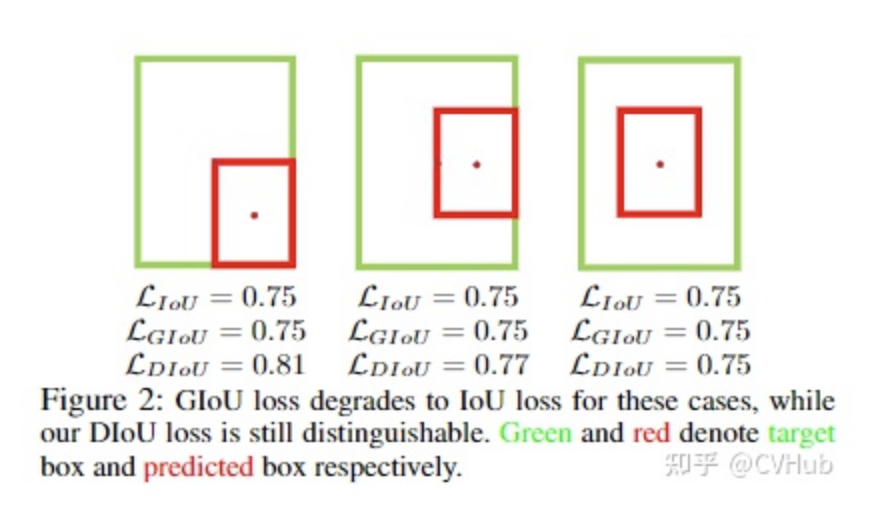
下圖表示的是GIoU損失（第一行）和DIoU損失（第二行）的一個(gè)訓(xùn)練過程收斂情況。其中綠色框?yàn)槟繕?biāo)邊框，黑色框?yàn)殄^框，藍(lán)色框和紅色框則分別表示使用GIoU損失和DIoU損失所得到的預(yù)測框。可以發(fā)現(xiàn)，GIoU損失一般會(huì)增加預(yù)測框的大小使其能和目標(biāo)框重疊，而DIoU損失則直接使目標(biāo)框和預(yù)測框之間的中心點(diǎn)歸一化距離最小，即讓預(yù)測框的中心快速的向目標(biāo)中心收斂。

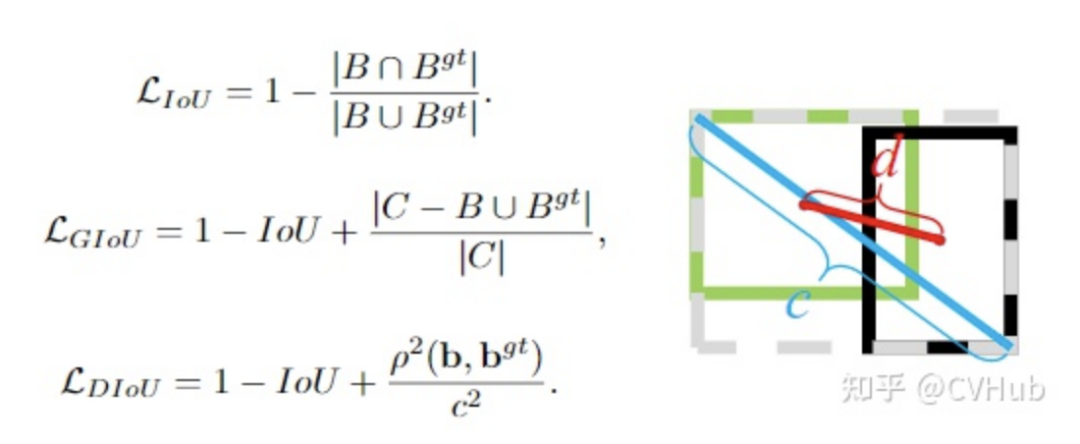
左圖給出這三個(gè)IoU損失所對應(yīng)的計(jì)算公式。對于DIoU來說，如圖右所示，其懲罰項(xiàng)由兩部分構(gòu)成：分子為目標(biāo)框和預(yù)測框中心點(diǎn)之間的歐式距離；分母為兩個(gè)框最小外接矩形框的兩個(gè)對角線距離。因此， 直接優(yōu)化兩個(gè)點(diǎn)之間的距離會(huì)使得模型收斂得更快，同時(shí)又能夠在兩個(gè)邊框不重疊的情況下給出一個(gè)優(yōu)化的方向。

• CIoU Loss

即完整IoU損失，全稱為Complete IoU loss，與DIoU出自同一篇論文。上面我們提到GIoU存在兩個(gè)缺陷，DIoU的提出解決了其實(shí)一個(gè)缺陷，即收斂速度的問題。而一個(gè)好的邊框回歸損失應(yīng)該同時(shí)考慮三個(gè)重要的幾何因素，即重疊面積（Overlap area）、中心點(diǎn)距離（Central point distance）和高寬比（Aspect ratio）。GIoU考慮到了重疊面積的問題，DIoU考慮到了重疊面積和中心點(diǎn)距離的問題，CIoU則在此基礎(chǔ)上進(jìn)一步的考慮到了高寬比的問題。

CIoU的計(jì)算公式如下所示，可以看出，其在DIoU的基礎(chǔ)上加多了一個(gè)懲罰項(xiàng)αv。其中α為權(quán)重為正數(shù)的重疊面積平衡因子，在回歸中被賦與更高的優(yōu)先級，特別是在兩個(gè)邊框不重疊的情況下；而v則用于測量寬高比的一致性。

• F-EIoU Loss

Focal and Efficient IoU Loss是由華南理工大學(xué)學(xué)者最近提出的一篇關(guān)于目標(biāo)檢測損失函數(shù)的論文，文章主要的貢獻(xiàn)是提升網(wǎng)絡(luò)收斂速度和目標(biāo)定位精度。目前檢測任務(wù)的損失函數(shù)主要有兩個(gè)缺點(diǎn)：(1)無法有效地描述邊界框回歸的目標(biāo)，導(dǎo)致收斂速度慢以及回歸結(jié)果不準(zhǔn)確（2）忽略了邊界框回歸中不平衡的問題。

F-EIou loss首先提出了一種有效的交并集（IOU）損失，它可以準(zhǔn)確地測量邊界框回歸中的重疊面積、中心點(diǎn)和邊長三個(gè)幾何因素的差異：

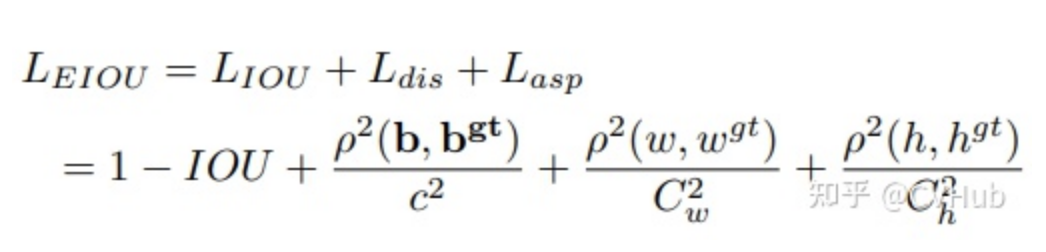
其次，基于對有效樣本挖掘問題（EEM）的探討，提出了Focal loss的回歸版本，以使回歸過程中專注于高質(zhì)量的錨框：

最后，將以上兩個(gè)部分結(jié)合起來得到Focal-EIou Loss：

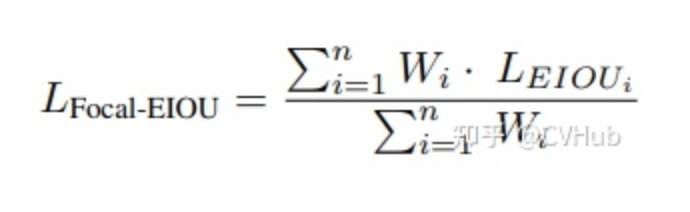
其中，通過加入每個(gè)batch的權(quán)重和來避免網(wǎng)絡(luò)在早期訓(xùn)練階段收斂慢的問題。

• CDIoU Loss

Control Distance IoU Loss是由同濟(jì)大學(xué)學(xué)者提出的，文章的主要貢獻(xiàn)是在幾乎不增強(qiáng)計(jì)算量的前提下有效提升了邊界框回歸的精準(zhǔn)度。目前檢測領(lǐng)域主要兩大問題：（1）SOTA算法雖然有效但計(jì)算成本高（2）邊界框回歸損失函數(shù)設(shè)計(jì)不夠合理。

文章首先提出了一種對于Region Propasl（RP）和Ground Truth（GT）之間的新評估方式，即CDIoU。可以發(fā)現(xiàn)，它雖然沒有直接中心點(diǎn)距離和長寬比，但最終的計(jì)算結(jié)果是有反應(yīng)出RP和GT的差異。計(jì)算公式如下：

對比以往直接計(jì)算中心點(diǎn)距離或是形狀相似性的損失函數(shù)，CDIoU能更合理地評估RP和GT的差異并且有效地降低計(jì)算成本。然后，根據(jù)上述的公式，CDIoU Loss可以定義為：

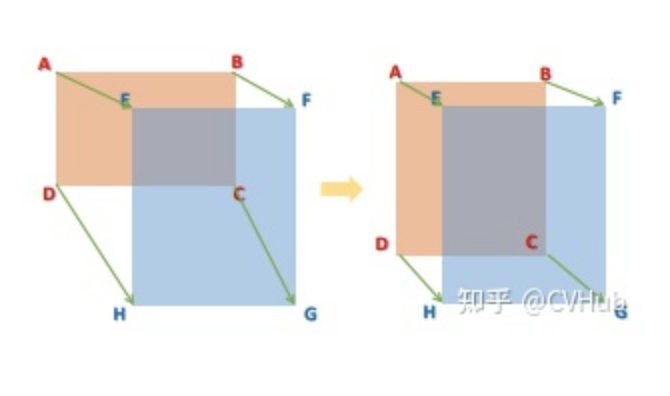
通過觀察這個(gè)公式，可以直觀地感受到，在權(quán)重迭代過程中，模型不斷地將RP的四個(gè)頂點(diǎn)拉向GT的四個(gè)頂點(diǎn)，直到它們重疊為止，如下圖所示：

2. 分類損失

• Entropy

即“熵”，熵的概念最早起源于物理學(xué)，用于度量一個(gè)熱力學(xué)系統(tǒng)的無序程度。但更常見的，在信息論里面， 熵是用于描述對不確定性的度量。所以，這個(gè)概念可以延伸到深度神經(jīng)網(wǎng)絡(luò)中，比如我們的模型在做分類時(shí)，其實(shí)也是在做一個(gè)判斷一個(gè)物體到底是不是屬于某個(gè)類別。因此，在正式介紹分類損失函數(shù)時(shí)，我們必須先了解熵的概念。

數(shù)字化時(shí)代，信息都是由Bits(0和1)組成的。在通信時(shí)，有些位是有用（useful）的信息，有些位則是冗余（redundant）的信息，有些位甚至是錯(cuò)誤（error）的信息，等等。當(dāng)我們傳達(dá)信息時(shí)，我們希望盡可能多地向接收者傳遞有用的信息。

傳輸1比特的信息意味著將接收者的不確定性降低2倍。—— 香濃

下面以一個(gè)天氣預(yù)報(bào)的例子為例，形象化的講解熵到底尤為何物？假設(shè)一個(gè)地方的天氣是隨機(jī)的，每天有50%的機(jī)會(huì)是晴天或雨天。

現(xiàn)在，如果氣象站告訴您明天將要下雨，那么他們將不確定性降低了2倍。起初，有兩種同樣可能的可能性，但是在收到氣象站的更新信息后，我們只有一種 。在這里，氣象站向我們發(fā)送了一點(diǎn)有用的信息，無論他們?nèi)绾尉幋a這些信息，這都是事實(shí)。即使發(fā)送的消息是雨天的，每個(gè)字符占一個(gè)字節(jié)，消息的總大小為40位，但它們?nèi)匀?strong style="font-weight: bold;color: black;">只通信1位的有用信息。現(xiàn)在，我們假設(shè)天氣有8種可能狀態(tài)，且都是等可能的。

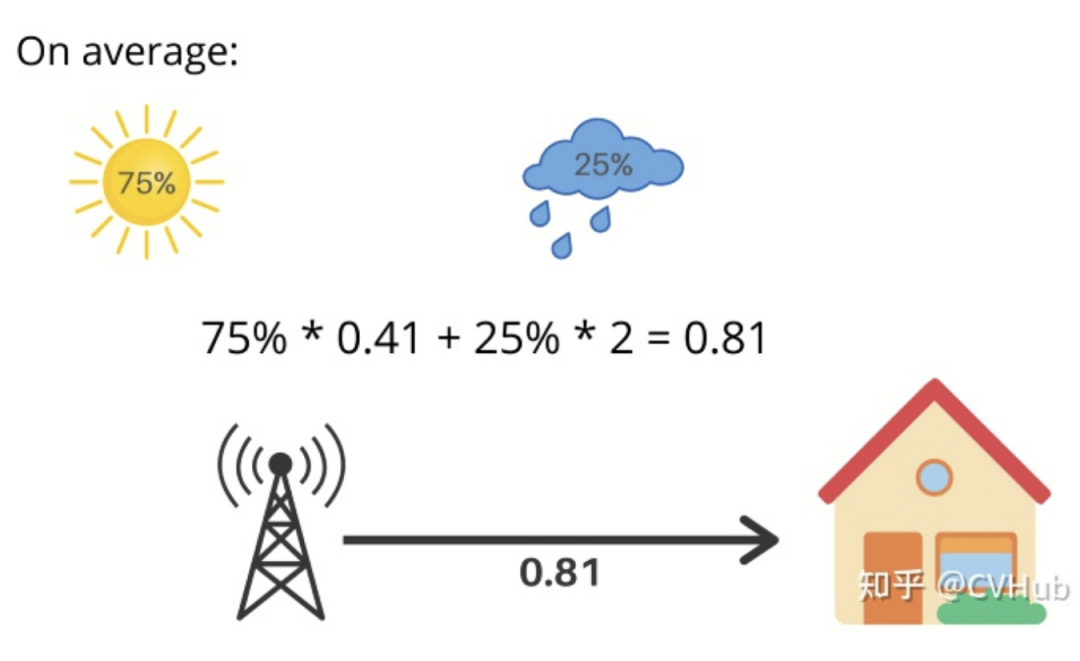
那么，當(dāng)氣象站為您提供第二天的天氣時(shí)，它們會(huì)將您的不確定性降低了8倍。由于每個(gè)事件的發(fā)生幾率為1/8，因此降低因子為8。但如果這些可能性不是等概率的呢？比如，75%的機(jī)會(huì)是晴天，25%的機(jī)會(huì)是雨天。

現(xiàn)在，如果氣象臺說第二天會(huì)下雨，那么你的不確定性就降低了4倍，也就是2比特的信息。不確定性的減少就是事件概率的倒數(shù)。在這種情況下，25%的倒數(shù)是4，log(4)以2為底得到2。因此，我們得到了2位有用的信息。

如果氣象站說第二天是晴天，那么我們得到0.41比特的有用信息。那么，我們平均能從氣象站得到多少信息呢？明天是晴天的概率是75%這就給了你0.41比特的信息而明天是雨天的概率是25%這就給了你2比特的信息，這就對應(yīng)我們平均每天從氣象站得到0.81比特的信息。

我們剛剛所計(jì)算出來的就叫做熵，它可以很好地描述事件的不確定性。它是由以下公式給出：

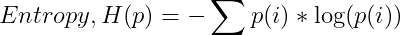
它衡量的是你每天了解天氣情況時(shí)所得到的平均信息量。一般來說，它給出了給定概率分布p中樣本值的平均信息量它告訴我們概率分布有多不可預(yù)測。如果我們住在沙漠中央，那里每天都是陽光燦爛的，平均來說，我們不會(huì)每天從氣象站得到很多信息。熵會(huì)接近于零。另一方面，如果天氣變化很大，熵就會(huì)大得多。

總的來說：一個(gè)事件的不確定性就越大，其信息量越大，它的熵值就越高。比如CVHub今日宣布上市。相反，如果一個(gè)時(shí)間的不確定性越小，其信息量越小，它的熵值就越低。比如CVHub今天又增加了一個(gè)讀者。

• Cross Entropy

現(xiàn)在，讓我們討論一下交叉熵。它只是平均信息長度。考慮同樣的例子，8種可能的天氣條件，所有都是等可能的，每一種都可以用3位編碼 [2^3=8]。

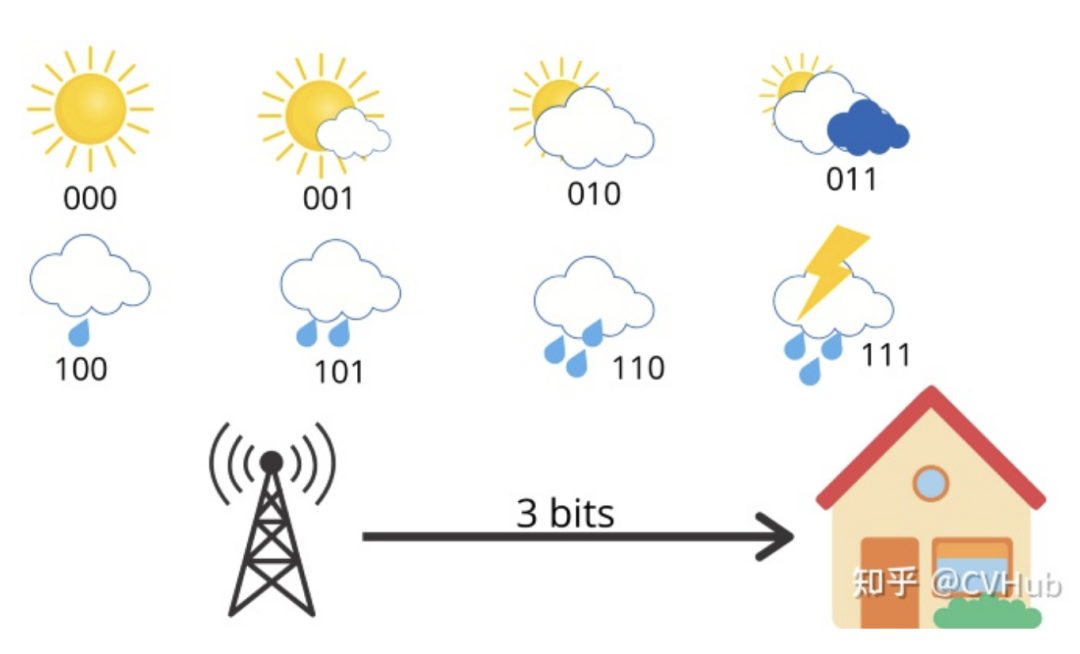
這里的平均信息長度是3，這就是交叉熵。但是現(xiàn)在，假設(shè)你住在一個(gè)陽光充足的地區(qū)，那里的天氣概率分布是這樣的：

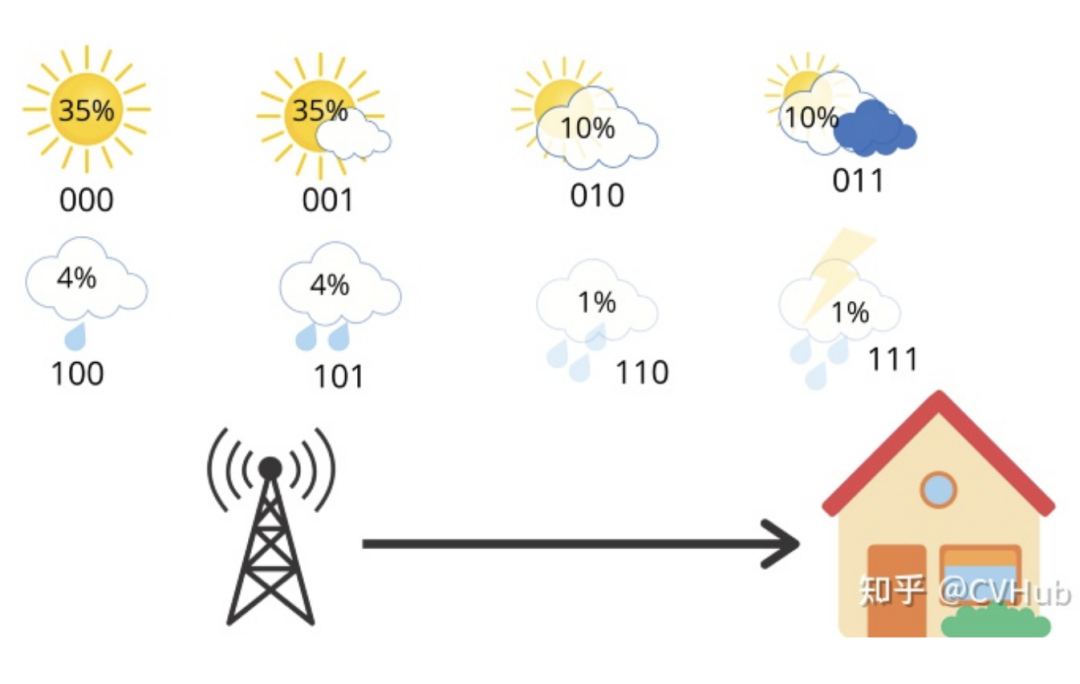
即每天有35%的機(jī)會(huì)出現(xiàn)晴天，只有1%的機(jī)會(huì)出現(xiàn)雷雨。我們可以計(jì)算這個(gè)概率分布的熵，我們得到2.23bits的熵，具體計(jì)算公式如下：

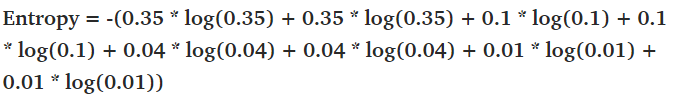
所以，平均來說，氣象站發(fā)送了3個(gè)比特，但接收者只得到2.23個(gè)比特有用的信息。但是，我們可以做得更好。例如，讓我們像這樣更改編碼方式：

現(xiàn)在，我們只使用2位用于表示晴天或部分晴天，使用3位用于多云和大部分多云，使用4位用于表示中雨和小雨，使用5位用于大雨和雷暴。天氣的編碼方式是明確的，并且如果你鏈接多條消息，則只有一種方法可以解釋位的順序。例如，01100只能表示部分晴天（01），然后是小雨（100）。因此，如果我們計(jì)算該站每天發(fā)送的平均比特?cái)?shù)，則可以得出：

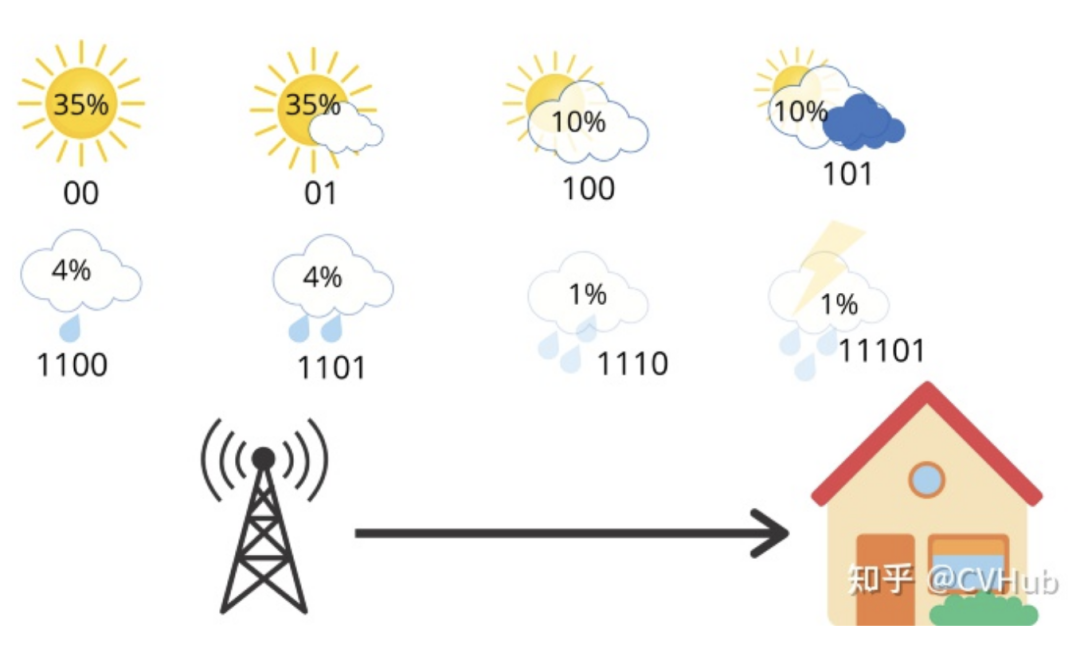
我們將得到4.58位。大約是熵的兩倍。平均而言，該站發(fā)送4.58位，但只有2.23位對接收者有用。每條消息發(fā)送的信息量是必要信息的兩倍。這是因?yàn)槲覀兪褂玫木幋a對天氣分布做出了一些隱含的假設(shè)。例如，當(dāng)我們在晴天使用2位消息時(shí)，我們隱式地預(yù)測晴天的概率為25％。以同樣的方式，我們計(jì)算所有天氣情況。

分母中2的冪對應(yīng)于用于傳輸消息的比特?cái)?shù)。很明顯，預(yù)測分布q和真實(shí)分布p有很大不同。現(xiàn)在我們可以把交叉熵表示成真實(shí)概率分布p的函數(shù)和預(yù)測概率分布q的函數(shù)：

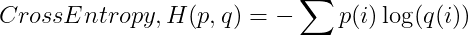
注意，這里對數(shù)的底數(shù)為2。

• K-L Divergence

即KL散度。對于交叉熵?fù)p失，除了我們在這里使用預(yù)測概率的對數(shù)（log(q(i))）外，它看起來與上面熵的方程非常相似。如果我們的預(yù)測是完美的，那就是預(yù)測分布等于真實(shí)分布，此時(shí)交叉熵就等于熵。但是，如果分布不同，則交叉熵將比熵大一些位數(shù)。交叉熵超過熵的量稱為相對熵，或更普遍地稱為庫爾貝克-萊布里埃發(fā)散度（KL Divergence）。總結(jié)如下：

接上面的例子，我們便可以順便算出：KL散度 = 交叉熵 - 熵 = 4.58 - 2.23 = 2.35（Bits）。通常來說，一般分類損失最常用的損失函數(shù)之一便是交叉熵?fù)p失。假設(shè)我們當(dāng)前做一個(gè)3個(gè)類別的圖像分類任務(wù)，如貓、狗、豬。給定一張輸入圖片其真實(shí)類別是貓，模型通過訓(xùn)練用Softmax分類后的輸出結(jié)果為：｛"cat": 0.3, "dog": 0.45, "pig": 0.25｝，那么此時(shí)交叉熵為：-1 * log(0.3) = 1.203。當(dāng)輸出結(jié)果為：｛"cat": 0.5, "dog": 0.3, "pig": 0.2｝時(shí)，交叉熵為：-1 * log(0.5) = 0.301。可以發(fā)現(xiàn)，當(dāng)真實(shí)類別的預(yù)測概率接近于0時(shí)，損失會(huì)變得非常大。但是當(dāng)預(yù)測值接近真實(shí)值時(shí)，損失將接近0。

• Dice Loss

即骰子損失，出自V-Net [3]，是一種用于評估兩個(gè)樣本之間相似性度量的函數(shù)，取值范圍為0~1，值越大表示兩個(gè)值的相似度越高，其基本定義（二分類）如下：

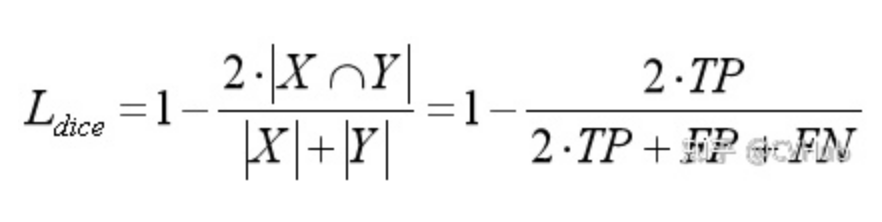
其中，|X∩Y|表示X和Y之間的交集，|X|和|Y|分別表示集合X和Y中像素點(diǎn)的個(gè)數(shù)，分子乘于2保證域值范圍在0~1之間，因?yàn)榉帜赶嗉訒r(shí)會(huì)計(jì)算多一次重疊區(qū)間，如下圖：

從右邊公式也可以看出，其實(shí)Dice系數(shù)是等價(jià)于F1分?jǐn)?shù)的，優(yōu)化Dice等價(jià)于優(yōu)化F1值。此外，為了防止分母項(xiàng)為0，一般我們會(huì)在分子和分母處同時(shí)加入一個(gè)很小的數(shù)作為平滑系數(shù)，也稱為拉普拉斯平滑項(xiàng)。Dice損失由以下兩個(gè)主要特性：

• 有益于正負(fù)樣本不均衡的情況，側(cè)重于對前景的挖掘；
• 訓(xùn)練過程中，在有較多小目標(biāo)的情況下容易出現(xiàn)振蕩；
• 極端情況下會(huì)出現(xiàn)梯度飽和的情況。

所以一般來說，我們都會(huì)結(jié)合交叉熵?fù)p失或者其他分類損失一同進(jìn)行優(yōu)化。

• Focal Loss

焦點(diǎn)損失，出自何凱明的《Focal Loss for Dense Object Detection》[4]，出發(fā)點(diǎn)是解決目標(biāo)檢測領(lǐng)域中one-stage算法如YOLO系列算法準(zhǔn)確率不高的問題。作者認(rèn)為樣本的類別不均衡（比如前景和背景）是導(dǎo)致這個(gè)問題的主要原因。比如在很多輸入圖片中，我們利用網(wǎng)格去劃分小窗口，大多數(shù)的窗口是不包含目標(biāo)的。如此一來，如果我們直接運(yùn)用原始的交叉熵?fù)p失，那么負(fù)樣本所占比例會(huì)非常大，主導(dǎo)梯度的優(yōu)化方向，即網(wǎng)絡(luò)會(huì)偏向于將前景預(yù)測為背景。即使我們可以使用OHEM（在線困難樣本挖掘）算法來處理不均衡的問題，雖然其增加了誤分類樣本的權(quán)重，但也容易忽略掉易分類樣本。而Focal loss則是聚焦于訓(xùn)練一個(gè)困難樣本的稀疏集，通過直接在標(biāo)準(zhǔn)的交叉熵?fù)p失基礎(chǔ)上做改進(jìn)，引進(jìn)了兩個(gè)懲罰因子，來減少易分類樣本的權(quán)重，使得模型在訓(xùn)練過程中更專注于困難樣本。其基本定義如下：

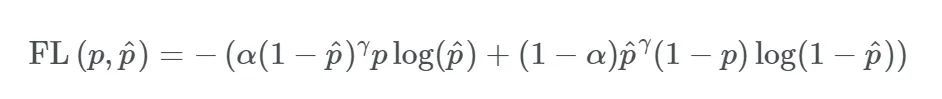
其中：

• 參數(shù) α 和 (1-α) 分別用于控制正/負(fù)樣本的比例，其取值范圍為[0, 1]。α的取值一般可通過交叉驗(yàn)證來選擇合適的值。
• 參數(shù) γ 稱為聚焦參數(shù)，其取值范圍為[0, +∞)，目的是通過減少易分類樣本的權(quán)重，從而使模型在訓(xùn)練時(shí)更專注于困難樣本。當(dāng) γ = 0 時(shí)，F(xiàn)ocal Loss就退化為交叉熵?fù)p失，γ 越大，對易分類樣本的懲罰力度就越大。

實(shí)驗(yàn)中，作者取（α=0.25，γ=0.2）的效果最好，具體還需要根據(jù)任務(wù)的情況調(diào)整。由此可見，應(yīng)用Focal-loss也會(huì)引入多了兩個(gè)超參數(shù)需要調(diào)整，而一般來說很需要經(jīng)驗(yàn)才能調(diào)好。

• Tversky loss

Tversky loss，發(fā)表于CVPR 2018上的一篇《Tversky loss function for image segmentation using 3D fully convolutional deep networks》文章 [5]，是根據(jù)Tversky 等人于1997年發(fā)表的《Features of Similarity》文章 [6] 所提出的Tversky指數(shù)所改造的。Tversky系數(shù)主要用于描述兩個(gè)特征（集合）之間的相似度，其定義如下：

由上可知，它是結(jié)合了Dice系數(shù)（F1-score）以及Jaccard系數(shù)（IoU）的一種廣義形式，如：

• 當(dāng) α = β = 0.5時(shí)，此時(shí)Tversky loss便退化為Dice系數(shù)（分子分母同乘于2）
• 當(dāng) α = β = 1時(shí)，此時(shí)Tversky loss便退化為Jaccard系數(shù)（交并比）

因此，我們只需控制 α 和 β 便可以控制假陰性和假陽性之間的平衡。比如在醫(yī)學(xué)領(lǐng)域我們要檢測腫瘤時(shí)，更多時(shí)候我們是希望Recall值（查全率，也稱為靈敏度或召回率）更高，因?yàn)槲覀儾幌Ｍf將腫瘤檢測為非腫瘤，即假陰性。因此，我們可以通過增大 β 的取值，來提高網(wǎng)絡(luò)對腫瘤檢測的靈敏度。其中，α + β 的取值我們一般會(huì)令其1。

總結(jié)

總的來說，損失函數(shù)的形式千變?nèi)f化，但追究溯源還是萬變不離其宗。其本質(zhì)便是給出一個(gè)能較全面合理的描述兩個(gè)特征或集合之間的相似性度量或距離度量，針對某些特定的情況，如類別不平衡等，給予適當(dāng)?shù)膽土P因子進(jìn)行權(quán)重的加減。大多數(shù)的損失都是基于最原始的損失一步步改進(jìn)的，或提出更一般的形式，或提出更加具體實(shí)例化的形式。

Reference：

如果覺得有用，就請分享到朋友圈吧！