思思热精品在线视频,看一级a片,在线观看黄色小视频,五月天激情导航,黄色片A视频,91在线导航,亚洲国产成人精品女人,麻豆激情

數(shù)據(jù)科學不僅僅是開發(fā)模型，也有很多像清洗數(shù)據(jù)和選擇有效特征的工作。將特征插入到一個具有相似的分布但是方式明顯不同的模型中，或者是在極不相同的尺度上，可能會導(dǎo)致錯誤的預(yù)測。解決這些問題的通用方法是首先使用“標準化”特征來消除均值和方差的顯著差異。

術(shù)語“標準化”可能會產(chǎn)生誤導(dǎo)(也不應(yīng)該與數(shù)據(jù)庫規(guī)范化混淆) ，因為它在統(tǒng)計學中有很多含義。然而，在標準化技術(shù)中有一個共同的主題，那就是將單獨的數(shù)據(jù)集對齊以便于比較。我們將關(guān)注的兩個技術(shù)是提取殘差，它改變了數(shù)據(jù)集的均值，以及重新縮放數(shù)據(jù)集中的值從0到1的尺度。

提取平均差

讓我們首先探索提取平均差技術(shù)。平均差是數(shù)據(jù)集中的值與數(shù)據(jù)集的平均值之間的相對差異。當數(shù)據(jù)集具有相似的分布但是方法明顯不同，從而使得數(shù)據(jù)集之間的比較變得困難時，這種技術(shù)非常有用。例如，假設(shè)我們有一個同等規(guī)模的兩個不同班級參加的考試。問題是一樣的，順序是一樣的，答案也是一樣的。然而，這兩個班級的平均分數(shù)是不同的。一班的平均成績是82分，二班的平均成績是77分。我們怎樣才能把這兩個班的成績合并起來呢？

讓我們從設(shè)置 Python 環(huán)境開始：

import numpy as npimport scipy.stats as stfrom sci_analysis import analyze%matplotlib inlinenp.random.seed(12)

上面的代碼導(dǎo)入 NumPy 包 as np，導(dǎo)入 scipy.stats as st 用于創(chuàng)建我們的數(shù)據(jù)集，sci_analysis 中的 analyze 函數(shù)可以用來繪圖最終結(jié)果，最后，我們設(shè)置隨機數(shù)生成器的種子值以使結(jié)果可重復(fù)。作為參數(shù)傳遞給 np.random.seed()的數(shù)字12是任意選擇的。現(xiàn)在，讓我們?yōu)槊總€類創(chuàng)建兩個數(shù)據(jù)集：

dist1 = st.norm.rvs(82, 4, size=25).astype(int)dist2 = st.norm.rvs(77, 7, size=25).astype(int)print(dist1)print(dist2)

輸出：

[83 79 82 75 85 75 82 81 78 93 79 83 86 77 87 81 86 78 77 86 84 82 84 84 77][61 65 64 61 72 73 76 78 74 75 77 70 72 77 72 72 76 86 79 74 72 76 92 54 80]

類1用 dist1表示，類2用 dist2表示。這兩個變量都是 NumPy 數(shù)組，由25個正態(tài)分布的隨機變量組成，dist1的平均值為82，標準差為4，dist2的平均值為77，標準差為7。兩個數(shù)組都被轉(zhuǎn)換為整數(shù)數(shù)據(jù)類型，以完成我們的考試成績示例。我們可以通過下面的代碼直觀地看到這個課程的分數(shù)：

analyze(    {'dist1': dist1, 'dist2': dist2},    title='Different means',    nqp=False,)print(f'dist1 mean: {np.mean(dist1)} std dev: {np.std(dist1)}')print(f'dist2 mean: {np.mean(dist2)} std dev: {np.std(dist2)}')

輸出：

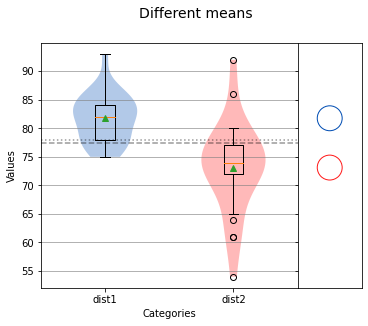
dist1 mean: 81.76 std dev: 4.197904239022134dist2 mean: 73.12 std dev: 7.7785345663563135

從上面的圖以及 dist1和 dist2的均值和標準差，我們可以判斷這些分布是不匹配的。

現(xiàn)在我們來計算 dist1和 dist2的平均差：

dist1_norm = dist1 - int(np.mean(dist1))dist2_norm = dist2 - int(np.mean(dist2))print(dist1_norm)print(dist2_norm)

輸出：

[   2  -2   1  -6   4   -6   1   0  -3  12   -2   2   5  -4   6    0   5  -3  -4   5    3   1   3   3  -4][ -12  -8  -9 -12  -1    0   3   5   1   2    4  -3  -1   4  -1   -1   3  13   6   1     -1   3  19 -19   7]

平均差是每個值與平均值之間的差值。換句話說，每個平均差是到每個分布的平均值（此時為0）的距離。由于每個分布現(xiàn)在都有一個平均值為零，它們現(xiàn)在可以直接相互比較。

analyze(    {'dist1': dist1_norm, 'dist2': dist2_norm},    title='Normalized',    nqp=False,)print(f'dist1 mean: {np.mean(dist1_norm)} std dev: {np.std(dist1_norm)}')print(f'dist2 mean: {np.mean(dist2_norm)} std dev: {np.std(dist2_norm)}')

輸出：

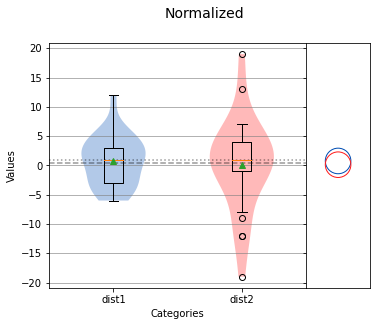
dist1 mean: 0.76 std dev: 4.197904239022134dist2 mean: 0.12 std dev: 7.7785345663563135

我們可以看到，平均值現(xiàn)在接近于零(如果將值轉(zhuǎn)換為整數(shù)時沒有舍入誤差，平均值將為零) ，但是每個分布的方差并沒有改變。這表明計算平均差是如何有效地改變每個分布的均值，以便對齊它們進行直接比較。

Min-Max Re-scaling

另一種標準化技術(shù)是重新縮放數(shù)據(jù)集。當試圖比較不同因素的數(shù)據(jù)集或使用不同單位的數(shù)據(jù)集時，比如比較英里數(shù)和米數(shù)時，這是非常有用的。讓我們生成兩個不同尺度（相差大概100倍）的數(shù)據(jù)：

dist3 = st.gamma.rvs(1.7, size=25)dist4 = st.gamma.rvs(120, size=25)print(dist3)print(dist4)

輸出：

[   0.49529541   1.42598239   0.38621773   0.96738928   0.53575876    1.72574991   0.3431045    0.80584646   0.77543188   1.84272915    2.049985     0.76373308   3.54020309   0.36979422   4.67967817    0.6311116    2.51371776   1.12812921   0.62183125   2.03923847    1.15269735   0.72795499   1.86093872   0.52560778   0.65314453] [113.88768554 108.94661696 118.40872068 124.94416222 150.91953839  116.86987547 107.05486021  89.61392457 126.28254195 123.32858014  108.31036684 114.52812809 109.43092709 114.17768634 114.54545154  111.21616394 102.08437696 127.42455395 105.82224292 127.28966453  114.03632754 120.02256655 120.77792085 103.43640076 112.24143473]

從上面的輸出中，你可以看到 dist3在0到10之間，dist4比 dist3大100倍。通過檢查平均值和標準差，我們可以看出這些分布是無法相互比較的。

analyze(    {"dist3": dist3, "dist4": dist4},    title="Different Scales",    nqp=False,)print(f'dist3 mean: {np.mean(dist3)} std dev: {np.std(dist3)}')print(f'dist4 mean: {np.mean(dist4)} std dev: {np.std(dist4)}')

輸出：

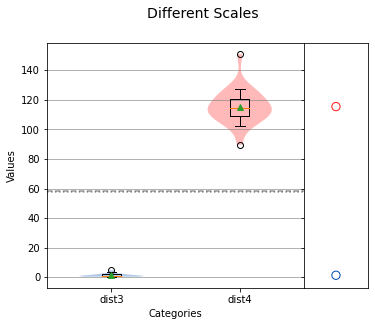
dist3 mean: 1.3024508282047844 std dev: 1.0372657584518052dist4 mean: 115.42402875045401 std dev: 11.29662689178773

幸運的是，我們可以通過每個數(shù)據(jù)集中的值和最小值的差值到最大值和最小值的差值的比值對數(shù)據(jù)進行處理。用公式表示如下：

    
     (x - min) / (max - min)

通過在 Python 中應(yīng)用這個方程，我們可以得到 dist3和 dist4的處理后的結(jié)果：

max = np.max(dist3)min = np.min(dist3)dist3_scaled = np.array([(x - min) / (max - min) for x in dist3])max = np.max(dist4)min = np.min(dist4)dist4_scaled = np.array([(x - min) / (max - min) for x in dist4])print(dist3_scaled)print(dist4_scaled)

輸出：

[0.03509474 0.24970817 0.00994177 0.14395807 0.04442546 0.3188336  0.         0.10670681 0.09969331 0.34580864 0.39360118 0.09699561 0.7372407  0.00615456 1.         0.06641352 0.50053647 0.18102418 0.0642735  0.39112306 0.18668952 0.08874529 0.35000771 0.04208467 0.07149424] [0.39594679 0.31534946 0.46969265 0.57629694 1.         0.44459144 0.28449166 0.         0.59812822 0.54994402 0.30497113 0.40639351 0.32324939 0.4006772  0.40667608 0.35236968 0.20341453 0.6167564  0.26438555 0.61455612 0.3983714  0.49601725 0.50833838 0.22546836 0.36909361]

通過重新縮放 dist3和 dist4，每個數(shù)據(jù)集的最大值現(xiàn)在是1，而最小值現(xiàn)在是0。這很方便，因為現(xiàn)在每個數(shù)據(jù)集都在同一尺度上，并且每個分布的形狀都保留了下來。實際上，每個分布都被壓縮并移動到0到1之間。現(xiàn)在，讓我們檢查一下重新縮放的 dist3和 dist4的平均標準差：

analyze(    {'dist3': dist3_scaled, 'dist4': dist4_scaled},    title='Scaled',    nqp=False,)print(f'dist3 mean: {np.mean(dist3_scaled)} std dev: {np.std(dist3_scaled)}')print(f'dist4 mean: {np.mean(dist4_scaled)} std dev:{np.std(dist4_scaled)}')

輸出：

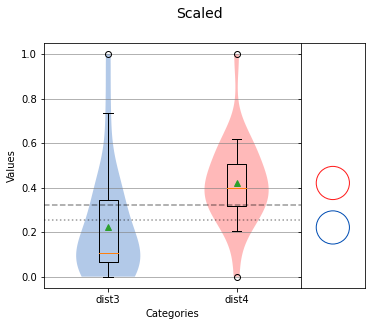
dist3 mean: 0.2212221913870349 std dev: 0.2391901615794912dist4 mean: 0.42100718959757816 std dev: 0.18426741349056594

我們現(xiàn)在可以看到，對于dist3_scaled和dist4_scaled，在相似的標準偏差下，兩者有著顯著的不同。

使用 NumPy 標準化大數(shù)據(jù)集

平均差和重新縮放都是用于分析的數(shù)據(jù)集標準化的有用技術(shù)。然而，這些數(shù)據(jù)集通常不止25個值，因此值得考慮如何計算平均差并有效地執(zhí)行重新縮放。值得慶幸的是，NumPy 可以幫助快速有效地執(zhí)行這些計算。

NumPy 是一個用于高性能科學計算的 Python 包。與使用常規(guī) Python 列表相比，NumPy 有兩個特性可以使計算更快、更高效。首先，NumPy 使用數(shù)組作為其主數(shù)據(jù)結(jié)構(gòu)，與 Python 列表相比，它使用的內(nèi)存更少，并且要求數(shù)組中的每個值都是相同的類型。數(shù)組也可以由標量操作ーー對數(shù)組的每個值應(yīng)用標量操作。實際上，我們在通過從分布(數(shù)組)中減去分布(標量)的平均值來計算平均差時已經(jīng)看到了這一點。

讓我們比較一下使用 Python 列表解析和數(shù)組操作計算平均差的速度差異。首先，我們創(chuàng)建一個隨機的、正態(tài)分布的變量數(shù)組，其值為100,000：

    
     dist5 = st.norm.rvs(82, 5, size=100000)

讓我們看看使用列表解析計算 dist5的平均差需要多長時間：

avg = np.mean(dist5)%timeit [val - avg for val in dist5]

輸出：

    
     10 loops, best of 3: 24.9 ms per loop

在 dist5中迭代每個值大約需要25毫秒，這個列表解析還不錯。然而，讓我們再次計算 dist5的平均差，但是使用 NumPy 標量操作：

avg = np.mean(dist5)%timeit dist5 - avg

輸出：

    
     10000 loops, best of 3: 144 μs per loop

僅僅從 dist5(NumPy 數(shù)組)減去平均值就需要144ms！這要感謝 NumPy 數(shù)組的高效設(shè)計。

現(xiàn)在，如果我們想要操作一個帶有函數(shù)的數(shù)組，而不僅僅是一個簡單的標量，那么該怎么辦呢？這是 NumPy 第二次以通用函數(shù)的形式提高 Python 的性能。通用函數(shù)是“向量化”操作，它利用 CPU 優(yōu)化來實現(xiàn)迭代數(shù)組中的每個值時的計算速度加快。NumPy 有許多內(nèi)置的通用函數(shù)，但我們也可以使用 NumPy 的 frompyfunc()函數(shù)編寫自己的函數(shù)。

讓我們來看看使用列表解析和自定義通用函數(shù)重新縮放數(shù)組值的速度差異：

min = np.min(dist5)max = np.max(dist5)%timeit [(val - min) / (max - min) for val in dist5]

輸出：

    
     10 loops, best of 3: 47.2 ms per loop

列表內(nèi)涵對dist5進行re-scale操作僅使用了47ms，可以實現(xiàn)令人欽佩的性能。讓我們將其與創(chuàng)建一個稱為 scale 的自定義通用函數(shù)相比較。

    
     scale = np.frompyfunc(lambda x, min, max: (x - min) / (max - min), 3, 1)

我們將使用 np.frompyfunc()函數(shù)，它接受一個可調(diào)用的、輸入的數(shù)量和輸出的數(shù)量作為參數(shù)。在這種情況下，可調(diào)用的是以 lambda 函數(shù)形式出現(xiàn)的重定標方程。如果您不熟悉 lambda 函數(shù)，可以將它們看作一行未命名的函數(shù)。我們的 lambda 函數(shù)有三個參數(shù): x、 min 和 max。這三個參數(shù)是在調(diào)用 np.frompyfunc()時指定的三個輸入。同樣值得注意的是，min 和 max 是由 dist5計算的標量，而 x 表示 dist5中的每個值。現(xiàn)在，讓我們計算 min 和 max 并調(diào)用 scale 函數(shù)：

min = np.min(dist5)max = np.max(dist5)%timeit scale(dist5, min, max).astype(float)

輸出：

    
     10 loops, best of 3: 20.4 ms per loop

正如你所看到的，自定義通用函數(shù)與列表解析相比只需要一半的時間就可以完成。

總結(jié)

我們研究了兩種歸一化技術(shù)：提取平均差和最小最大值重新縮放。提取平均差可以被認為是一個分布的轉(zhuǎn)移，所以它的平均值是0。最小-最大值重新縮放可以被認為是移動和壓縮數(shù)據(jù)集的分布，以便取值歸一化值0和1之間。平均差提取可用于比較不同方法但具有相似分布的情況。最小-最大值重新縮放是比較不同尺度和不同形狀分布的有用方法。

當分布被表示為 NumPy 數(shù)組時，這兩種規(guī)范化技術(shù)都可以通過 NumPy 有效地執(zhí)行。NumPy 數(shù)組上的標量操作快速且易于讀取。當需要對數(shù)組進行更復(fù)雜的操作時，可以使用通用函數(shù)高效地執(zhí)行操作。

· END ·

HAPPY LIFE

      
       

      
      
       個人微信（如果沒有備注不拉群！）
      
      
       請注明：地區(qū)+學校/企業(yè)+研究方向+昵稱
      
      
       

      


下載1：何愷明頂會分享

在「AI算法與圖像處理」公眾號后臺回復(fù)：何愷明，即可下載。總共有6份PDF，涉及 ResNet、Mask RCNN等經(jīng)典工作的總結(jié)分析

下載2：終身受益的編程指南：Google編程風格指南

在「AI算法與圖像處理」公眾號后臺回復(fù)：c++，即可下載。歷經(jīng)十年考驗，最權(quán)威的編程規(guī)范！

    
     下載3 CVPR2020
    
    
     

    
    
     在「AI算法與圖像處理」公眾號后臺回復(fù)：CVPR2020，即可下載1467篇CVPR 2020論文

覺得不錯就點亮在看吧

使用 NumPy 的標準化技巧