作者：鐘陽揚(yáng)

審校：陳之炎

圖(Graph)是一種數(shù)據(jù)結(jié)構(gòu), 能夠很自然地建模現(xiàn)實場景中一組實體之間的復(fù)雜關(guān)系。在真實世界中，很多數(shù)據(jù)往往以圖的形式出現(xiàn), 例如社交網(wǎng)絡(luò)、電商購物、蛋白質(zhì)相互作用關(guān)系等。因此，近些年來使用智能化方式來建模分析圖結(jié)構(gòu)的研究越來越受到關(guān)注, 其中基于深度學(xué)習(xí)的圖建模方法的圖神經(jīng)網(wǎng)絡(luò)(Graph Neural Network, GNN), 因其出色的性能已廣泛應(yīng)用于社會科學(xué)、自然科學(xué)等多個領(lǐng)域。

基本概念

1.1 圖的基本概念

通常使用G=(V, E)來表示圖，其中V表示節(jié)點(diǎn)的集合、E表示邊的集合。對于兩個相鄰節(jié)點(diǎn)u, v, 使用e=(u,v)表示這兩個節(jié)點(diǎn)之間的邊。兩個節(jié)點(diǎn)之間邊既可能是有向，也可能無向。若有向，則稱之有向圖(Directed Graph), 反之，稱之為無向圖(Undirected Graph)。

1.2 圖的表示

在圖神經(jīng)網(wǎng)絡(luò)中，常見的表示方法有鄰接矩陣、度矩陣、拉普拉斯矩陣等。

1)鄰接矩陣(Adjacency Matrix)

用于表示圖中節(jié)點(diǎn)之間的關(guān)系，對于n個節(jié)點(diǎn)的簡單圖，有鄰接矩陣: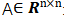

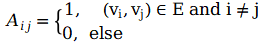
2)度矩陣(Degree Matrix)

節(jié)點(diǎn)的度(Degree)表示與該節(jié)點(diǎn)相連的邊的個數(shù)，記作d(v)。對于n個節(jié)點(diǎn)的簡單圖G=(V, E)，其度矩陣D為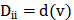，也是一個對角矩陣。

3）拉普拉斯矩陣 (Laplacian Matrix)

對于n個節(jié)點(diǎn)的簡單圖G=(V, E)，其拉普拉斯矩陣定義為L=D-A，其中D、A為上面提到過的度矩陣和鄰接矩陣. 將其歸一化后有。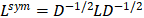

1.3 圖神經(jīng)網(wǎng)絡(luò)基本概念

圖神經(jīng)網(wǎng)絡(luò)(GNN)最早由Marco Gori [1]、Franco Scarselli [2,3]等人提出，他們將神經(jīng)網(wǎng)絡(luò)方法拓展到了圖數(shù)據(jù)計算領(lǐng)域。在Scarselli論文中典型的圖如圖1所示：

圖1 典型的圖神經(jīng)網(wǎng)絡(luò)

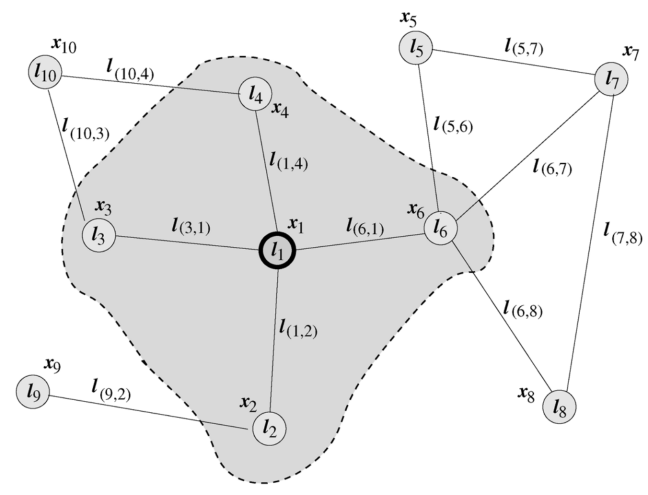
為了根據(jù)輸入節(jié)點(diǎn)鄰居信息更新節(jié)點(diǎn)狀態(tài)，將局部轉(zhuǎn)移函數(shù)f定義為循環(huán)遞歸函數(shù)的形式, 每個節(jié)點(diǎn)以周圍鄰居節(jié)點(diǎn)和相連的邊作為來源信息來更新自身的表達(dá)h。為了得到節(jié)點(diǎn)的輸出o, 引入局部輸出函數(shù)g。因此，有以下定義：

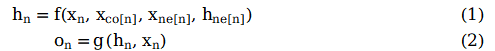
其中x表示節(jié)點(diǎn)投中, h表示節(jié)點(diǎn)隱狀態(tài)，ne[n]表示表示節(jié)點(diǎn)n的鄰居節(jié)點(diǎn)集合，co[n]表示節(jié)點(diǎn)n的鄰接邊的集合。以圖1的L1節(jié)點(diǎn)為例，X1是其輸入特征,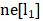包含節(jié)點(diǎn) 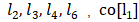, 包含邊。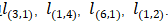

將所有局部轉(zhuǎn)移函數(shù)f堆疊起來, 有：

其中F是全局轉(zhuǎn)移函數(shù)(Global Transition Function), G是全局輸出函數(shù)(Global Output Function)。

根據(jù)巴拿赫不動點(diǎn)定理[4]，假設(shè)公式(3)的F是壓縮映射，那么不動點(diǎn)H的值就可以唯一確定，根據(jù)以下方式迭代求解:

基于不動點(diǎn)定理，對于任意初始值，GNN會按照公式(5)收斂到公式(3)描述的解。

經(jīng)典模型

2.1 GCN-開山之作

2017年，Thomas N. Kipf等人提出GCN[5]. 其結(jié)構(gòu)如圖2所示：

圖2 Thomas N. Kipf等人提出GCN

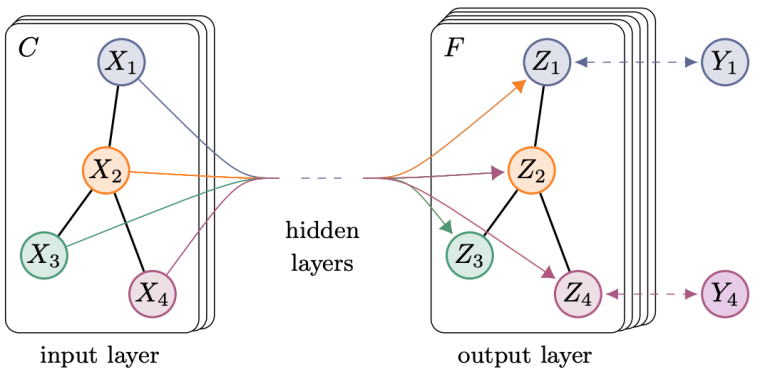
假設(shè)需要構(gòu)造一個兩層的GCN，激活函數(shù)分別采用ReLU和Softmax，則整體的正向傳播的公式如下所示：

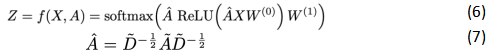
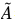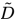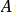其中W0表示第一層的權(quán)重矩陣，W1表示第二層的權(quán)重矩陣，X為節(jié)點(diǎn)特征，等于鄰接矩陣A和單位矩陣相加，為的度矩陣。

從上面的正向傳播公式和示意圖來看，GCN好像跟基礎(chǔ)GNN沒什么區(qū)別。接下里給出GCN的傳遞公式(8)：

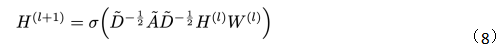
觀察一下歸一化的矩陣與特征向量矩陣的乘積：

來源：

https://www.zhihu.com/question/426784258

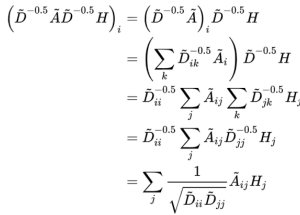
可以發(fā)現(xiàn)，GCN引入度矩陣D用于對鄰接矩陣的歸一化后，層間傳播將不再單單地對領(lǐng)域節(jié)特征點(diǎn)取平均，它不僅考慮了節(jié)點(diǎn)i對度，也考慮了鄰接節(jié)點(diǎn)j的度，對于度數(shù)較大的節(jié)點(diǎn)，它在聚合時貢獻(xiàn)地會更少。

文章[5]通過實驗證明GCN性能出色，GCN即使不訓(xùn)練，提取出來的特征已經(jīng)非常優(yōu)秀,作者做了一個實驗，使用俱樂部關(guān)系網(wǎng)絡(luò)數(shù)據(jù)，如圖3所示：

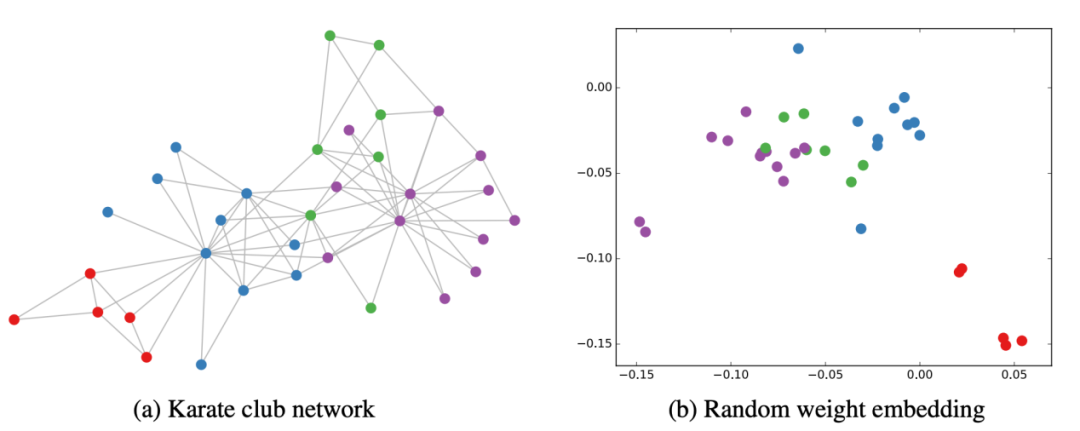
圖3 GCN在空間上自動聚類從上圖可以發(fā)現(xiàn)，使用隨機(jī)初始化的GCN進(jìn)行特征提取，經(jīng)過GCN的提取出的embedding，已經(jīng)在空間上自動聚類了。

2.2 GAT - attention機(jī)制

GAT[6]是典型的基于注意力機(jī)制的圖神經(jīng)網(wǎng)絡(luò)。圖注意網(wǎng)絡(luò)結(jié)構(gòu)如圖4所示,節(jié)點(diǎn)i，j的特征作為輸出，計算兩節(jié)點(diǎn)之間的注意力權(quán)重。

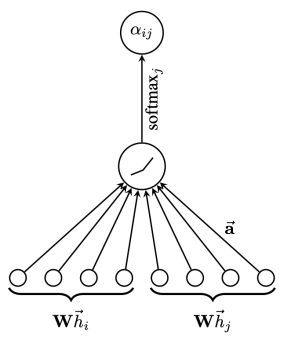
圖4 圖注意網(wǎng)絡(luò)結(jié)構(gòu)

對于節(jié)點(diǎn)i,j 的注意力系數(shù)（Attention Coefficients）計算方式為：

其中W是一個共享參數(shù)的線性映射對于節(jié)點(diǎn)特征的增維，h就是節(jié)點(diǎn)的特征，a(W，W)可以表示兩個向量內(nèi)積計算相似度。再經(jīng)過softmax得到注意力權(quán)重：

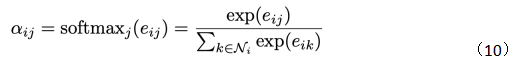
那么有如下注意力權(quán)重計算公式：

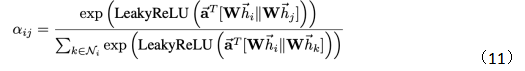
其中Ni表示節(jié)點(diǎn)i的鄰居節(jié)點(diǎn)，||表示特征拼接。

最終節(jié)點(diǎn)的輸出如下公式所示，很好理解，就是給鄰居節(jié)點(diǎn)分配不同的權(quán)重來聚合信息。

在文章[6]中，作者還引入了多頭注意力，結(jié)構(gòu)如圖5所示，公式如（13）所示：

圖5 多頭注意力機(jī)制結(jié)構(gòu)

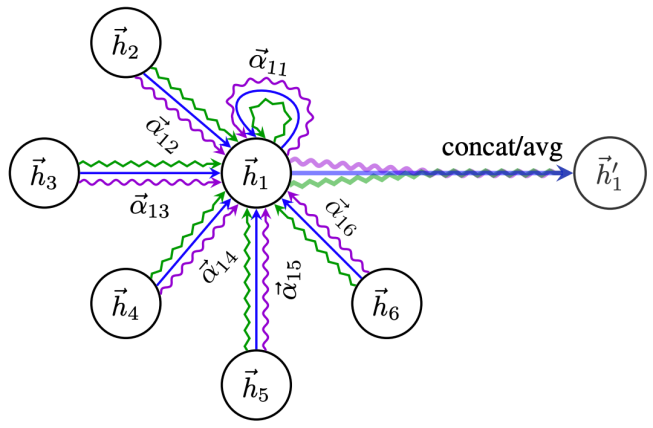
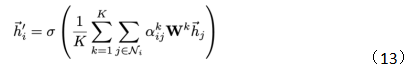
多頭注意力本質(zhì)是引入并行的幾個獨(dú)立的注意力機(jī)制，可以提取信息中的多重含義，防止過擬合。

2.3 GraphSAGE -歸納式學(xué)習(xí)框架

提到GraphSAGE[7]模型, 不得不又提到GCN，我們回顧一下GCN的迭代公式：

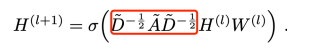
圖中紅框位置所做的操作可以簡單理解為對鄰接矩陣A的歸一化變換，去掉該部分會發(fā)現(xiàn)剩下的結(jié)構(gòu)等同于深度神經(jīng)網(wǎng)絡(luò)，加上紅色部分后，通過矩陣乘法實際上所做的就是將節(jié)點(diǎn)與節(jié)點(diǎn)相鄰節(jié)點(diǎn)特征信息進(jìn)行相加。

GraphSAGE在特征聚合方式上與GCN簡單相加不同，GraphSAGE支持max-pooling、LSTM、mean等聚合方式。另外，GraphSAGE與GCN的最大不同點(diǎn)在于，GCN是直推式方法，即所有節(jié)點(diǎn)都在圖中，對于新出現(xiàn)的節(jié)點(diǎn)無法處理。GraphSAGE是歸納式，對于沒見過的節(jié)點(diǎn)也能生成embedding。

GraphSAGE的傳播方法如圖6所示：

圖6 GraphSAGE的傳播方法

可以看到對于圖G中的某個節(jié)點(diǎn)v，需要聚合k層信息，那么先有個對層數(shù)遍歷的for循環(huán)，第二層循環(huán)便是遍歷節(jié)點(diǎn)v的鄰居節(jié)點(diǎn)，然后通過聚合函數(shù)AGGEGATE(可以是mean、max、LSTM或者其他)來聚合k-1層的鄰居節(jié)點(diǎn)信息，得到聚合后的k層鄰居節(jié)點(diǎn)信息，然后將聚合后的k層鄰居節(jié)點(diǎn)信息與k-1層節(jié)點(diǎn)v的信息進(jìn)行拼接，然后通過權(quán)重參數(shù)W進(jìn)行計算得到K層關(guān)于節(jié)點(diǎn)v的信息。

直觀一點(diǎn)，可以看看下面這幅圖：

圖7 圖節(jié)點(diǎn)的傳播方式

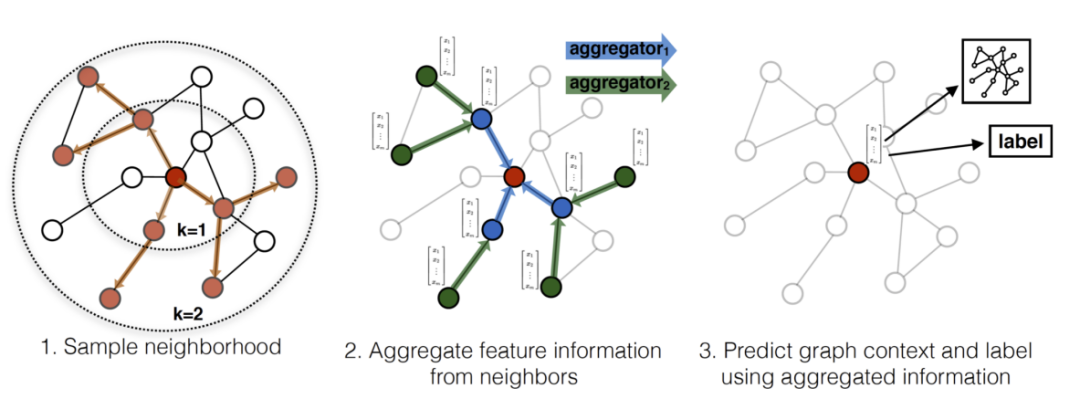
以為紅色節(jié)點(diǎn)為目標(biāo)節(jié)點(diǎn)，在一次步驟中，對紅色節(jié)點(diǎn)的一階鄰居和二階段鄰居做隨機(jī)采樣。然后通過聚合策略，把節(jié)點(diǎn)的特征信息從二階鄰居聚合到目標(biāo)節(jié)點(diǎn)上，然后用更新后的目標(biāo)節(jié)點(diǎn)的表征可以應(yīng)用到不同需求的任務(wù)上。

結(jié)論

綜上所述，GraphSAGE相對于GCN可以避免需要一次性加載整張網(wǎng)絡(luò)、能夠靈活設(shè)計聚合方式、具備Transductive性質(zhì)。可以適配測試集的節(jié)點(diǎn)變化，不需要像GCN一樣會因為節(jié)點(diǎn)變化造成拉普拉斯矩陣變化導(dǎo)致需要重新訓(xùn)練模型。

參考文獻(xiàn)

[1] M. Gori, G. Monfardini and F. Scarselli, "A new model for learning in graph domains," Proceedings. 2005 IEEE International Joint Conference on Neural Networks, 2005., 2005, pp. 729-734 vol. 2, doi: 10.1109/IJCNN.2005.1555942.

[2] Scarselli F , Tsoi A C , Gori M , et al. Graphical-Based Learning Environments for Pattern Recognition[J]. DBLP, 2004.

[3]Franco,Scarselli,Marco,Gori,AhChung,Tsoi,Markus,Hagenbuchner,Gabriele,Monfardini.The graph neural network model.[J].IEEE transactions on neural networks,2009,20(1):61-80.DOI:10.1109/TNN.2008.2005605.

[4]MA Khamsi, WA Kirk. An Introduction to Metric Spaces and Fixed Point Theory. 2011.

[5] Kipf T N , Welling M . Semi-Supervised Classification with Graph Convolutional Networks[J]. 2016.

[6] Velikovi P , Cucurull G , Casanova A , et al. Graph Attention Networks[J]. 2017.

[7] W. Hamilton, Z. Ying and J. Leskovec, "Inductive representation learning on large graphs" in Advances in Neural Information Processing Systems, pp. 1025-1035, 2017.

作者簡介

鐘陽揚(yáng)，數(shù)據(jù)派研究部志愿者，碩士畢業(yè)于東北大學(xué)，主要研究方向為計算機(jī)視覺、圖神經(jīng)網(wǎng)絡(luò)等。

編輯：于騰凱

校對：林亦霖

>>更多閱讀

數(shù)據(jù)分析師必需具備的10種分析思維
網(wǎng)易用戶體驗研究中心：游戲交易網(wǎng)絡(luò)的洞察分析
為什么大多數(shù)據(jù)分析失敗的原因分析及解決策略

一文讀懂圖神經(jīng)網(wǎng)絡(luò)

作者：鐘陽揚(yáng)

審校：陳之炎