一文讀懂機器學習中的正則化

極市導讀
?正則化是一種為了減小測試誤差的行為(有時候會增加訓練誤差)。當我們用較為復雜的模型擬合數(shù)據(jù)時,容易出現(xiàn)過擬合現(xiàn)象,導致模型的泛化能力下降,這時我們就需要使用正則化,降低模型的復雜度。本文總結(jié)闡釋了正則化的相關知識點,幫助大家更好的理解正則化這一概念。>>加入極市CV技術交流群,走在計算機視覺的最前沿
目錄
LP范數(shù)
L1范數(shù)
L2范數(shù)
L1范數(shù)和L2范數(shù)的區(qū)別
Dropout
Batch Normalization
歸一化、標準化 & 正則化
Reference
在總結(jié)正則化(Regularization)之前,我們先談一談正則化是什么,為什么要正則化。
個人認為正則化這個字眼有點太過抽象和寬泛,其實正則化的本質(zhì)很簡單,就是對某一問題加以先驗的限制或約束以達到某種特定目的的一種手段或操作。在算法中使用正則化的目的是防止模型出現(xiàn)過擬合。一提到正則化,很多同學可能馬上會想到常用的L1范數(shù)和L2范數(shù),在匯總之前,我們先看下LP范數(shù)是什么鬼。
LP范數(shù)
范數(shù)簡單可以理解為用來表征向量空間中的距離,而距離的定義很抽象,只要滿足非負、自反、三角不等式就可以稱之為距離。
LP范數(shù)不是一個范數(shù),而是一組范數(shù),其定義如下:
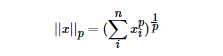
p
根據(jù)p

上圖表示了p
那問題來了,L0范數(shù)是啥玩意?
L0范數(shù)表示向量中非零元素的個數(shù),用公式表示如下:
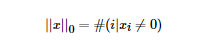
我們可以通過最小化L0范數(shù),來尋找最少最優(yōu)的稀疏特征項。但不幸的是,L0范數(shù)的最優(yōu)化問題是一個NP hard問題(L0范數(shù)同樣是非凸的)。因此,在實際應用中我們經(jīng)常對L0進行凸松弛,理論上有證明,L1范數(shù)是L0范數(shù)的最優(yōu)凸近似,因此通常使用L1范數(shù)來代替直接優(yōu)化L0范數(shù)。
L1范數(shù)
根據(jù)LP范數(shù)的定義我們可以很輕松的得到L1范數(shù)的數(shù)學形式:
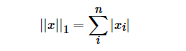
通過上式可以看到,L1范數(shù)就是向量各元素的絕對值之和,也被稱為是"稀疏規(guī)則算子"(Lasso regularization)。那么問題來了,為什么我們希望稀疏化?稀疏化有很多好處,最直接的兩個:
特征選擇
可解釋性
L2范數(shù)
L2范數(shù)是最熟悉的,它就是歐幾里得距離,公式如下:
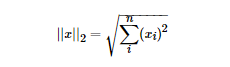
L2范數(shù)有很多名稱,有人把它的回歸叫“嶺回歸”(Ridge Regression),也有人叫它“權(quán)值衰減”(Weight Decay)。以L2范數(shù)作為正則項可以得到稠密解,即每個特征對應的參數(shù)w
L1范數(shù)和L2范數(shù)的區(qū)別
引入PRML一個經(jīng)典的圖來說明下L1和L2范數(shù)的區(qū)別,如下圖所示:
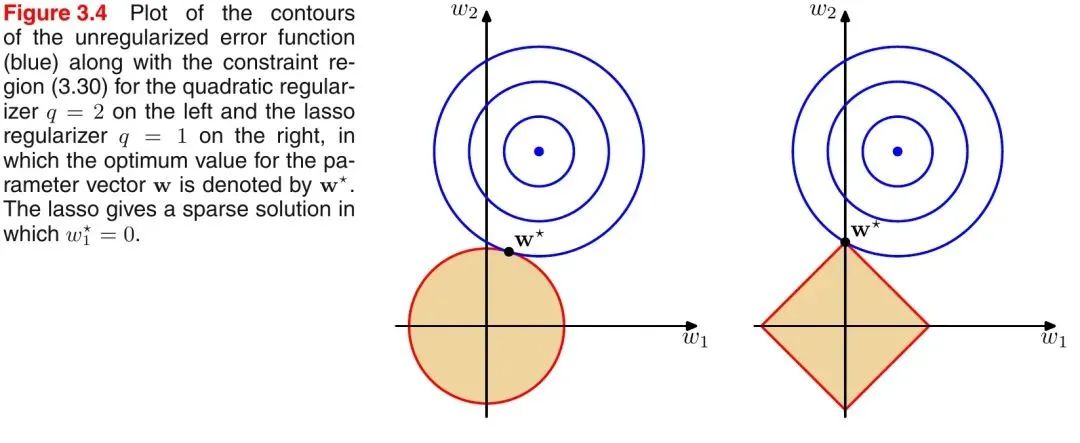
?
如上圖所示,藍色的圓圈表示問題可能的解范圍,橘色的表示正則項可能的解范圍。而整個目標函數(shù)(原問題+正則項)有解當且僅當兩個解范圍相切。從上圖可以很容易地看出,由于L2范數(shù)解范圍是圓,所以相切的點有很大可能不在坐標軸上,而由于L1范數(shù)是菱形(頂點是凸出來的),其相切的點更可能在坐標軸上,而坐標軸上的點有一個特點,其只有一個坐標分量不為零,其他坐標分量為零,即是稀疏的。所以有如下結(jié)論,L1范數(shù)可以導致稀疏解,L2范數(shù)導致稠密解。
從貝葉斯先驗的角度看,當訓練一個模型時,僅依靠當前的訓練數(shù)據(jù)集是不夠的,為了實現(xiàn)更好的泛化能力,往往需要加入先驗項,而加入正則項相當于加入了一種先驗。
L1范數(shù)相當于加入了一個Laplacean先驗;
L2范數(shù)相當于加入了一個Gaussian先驗。
如下圖所示:
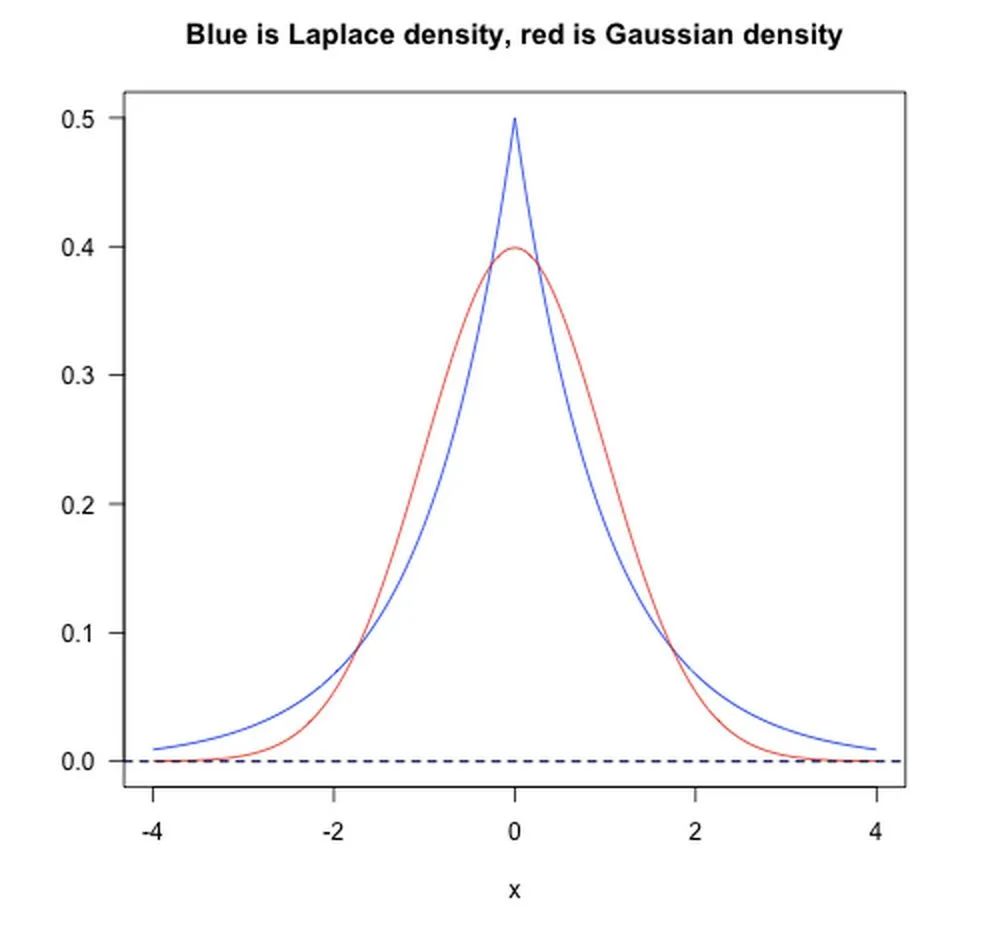
Dropout
Dropout是深度學習中經(jīng)常采用的一種正則化方法。它的做法可以簡單的理解為在DNNs訓練的過程中以概率p
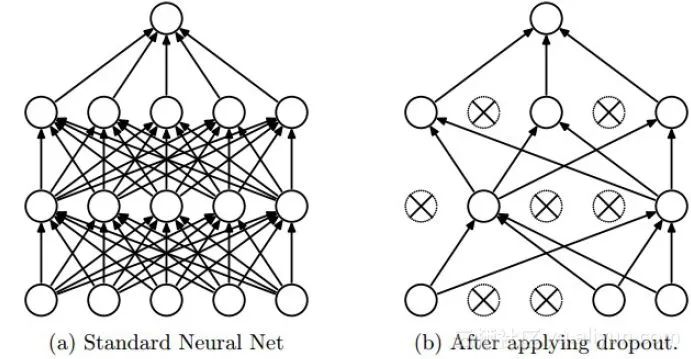
我們可以從兩個方面去直觀地理解Dropout的正則化效果:
在Dropout每一輪訓練過程中隨機丟失神經(jīng)元的操作相當于多個DNNs進行取平均,因此用于預測時具有vote的效果。
減少神經(jīng)元之間復雜的共適應性。當隱藏層神經(jīng)元被隨機刪除之后,使得全連接網(wǎng)絡具有了一定的稀疏化,從而有效地減輕了不同特征的協(xié)同效應。也就是說,有些特征可能會依賴于固定關系的隱含節(jié)點的共同作用,而通過Dropout的話,就有效地組織了某些特征在其他特征存在下才有效果的情況,增加了神經(jīng)網(wǎng)絡的魯棒性。
Batch Normalization
批規(guī)范化(Batch Normalization)嚴格意義上講屬于歸一化手段,主要用于加速網(wǎng)絡的收斂,但也具有一定程度的正則化效果。
這里借鑒下魏秀參博士的知乎回答中對covariate shift的解釋(https://www.zhihu.com/question/38102762)。
注:以下內(nèi)容引自魏秀參博士的知乎回答
大家都知道在統(tǒng)計機器學習中的一個經(jīng)典假設是“源空間(source domain)和目標空間(target domain)的數(shù)據(jù)分布(distribution)是一致的”。如果不一致,那么就出現(xiàn)了新的機器學習問題,如transfer learning/domain adaptation等。而covariate shift就是分布不一致假設之下的一個分支問題,它是指源空間和目標空間的條件概率是一致的,但是其邊緣概率不同。大家細想便會發(fā)現(xiàn),的確,對于神經(jīng)網(wǎng)絡的各層輸出,由于它們經(jīng)過了層內(nèi)操作作用,其分布顯然與各層對應的輸入信號分布不同,而且差異會隨著網(wǎng)絡深度增大而增大,可是它們所能“指示”的樣本標記(label)仍然是不變的,這便符合了covariate shift的定義。
BN的基本思想其實相當直觀,因為神經(jīng)網(wǎng)絡在做非線性變換前的激活輸入值(X=WU+B
歸一化、標準化 & 正則化
正則化我們以及提到過了,這里簡單提一下歸一化和標準化。
歸一化(Normalization):歸一化的目標是找到某種映射關系,將原數(shù)據(jù)映射到
一般有兩種應用場景:
把數(shù)變?yōu)?0, 1)之間的小數(shù)
把有量綱的數(shù)轉(zhuǎn)化為無量綱的數(shù)
常用min-max normalization:
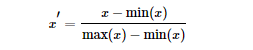
標準化(Standardization):用大數(shù)定理將數(shù)據(jù)轉(zhuǎn)化為一個標準正態(tài)分布,標準化公式為:
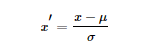
歸一化和標準化的區(qū)別:
我們可以這樣簡單地解釋:
歸一化的縮放是“拍扁”統(tǒng)一到區(qū)間(僅由極值決定),而標準化的縮放是更加“彈性”和“動態(tài)”的,和整體樣本的分布有很大的關系。
值得注意:
歸一化:縮放僅僅跟最大、最小值的差別有關。
標準化:縮放和每個點都有關系,通過方差(variance)體現(xiàn)出來。與歸一化對比,標準化中所有數(shù)據(jù)點都有貢獻(通過均值和標準差造成影響)。
為什么要標準化和歸一化?
提升模型精度:歸一化后,不同維度之間的特征在數(shù)值上有一定比較性,可以大大提高分類器的準確性。
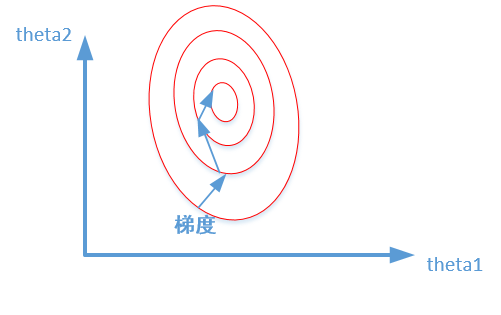
加速模型收斂:標準化后,最優(yōu)解的尋優(yōu)過程明顯會變得平緩,更容易正確的收斂到最優(yōu)解。如下圖所示:
推薦閱讀

