日韩三A片一,国产精品久久久久久久激情视频,欧美自拍视频在线观看?,欧美性生交XXXXX,黄色片免费观看,国产性爱无码视频,艹逼视频免费观看,少妇一级婬片60分钟一

一、數(shù)據(jù)挖掘簡介

數(shù)據(jù)挖掘是一個通過對大量數(shù)據(jù)進(jìn)行清理和處理，以發(fā)現(xiàn)其中隱藏的信息和模式的過程。簡單來說，它是從大量數(shù)據(jù)中提取或“挖掘”知識的過程，也稱為知識發(fā)現(xiàn)。

隨著互聯(lián)網(wǎng)和移動工具的發(fā)展，我們每天產(chǎn)生的數(shù)據(jù)量非常龐大，這些數(shù)據(jù)通常被收集并存儲在大型數(shù)據(jù)庫中。數(shù)據(jù)挖掘技術(shù)提供了一種有效的方法，可以從這些海量數(shù)據(jù)中提取有價值的信息，從而為決策提供重要依據(jù) 。這個過程在許多領(lǐng)域都有廣泛的應(yīng)用，如新聞分類、推薦系統(tǒng)等。

數(shù)據(jù)挖掘一般的流程如下：

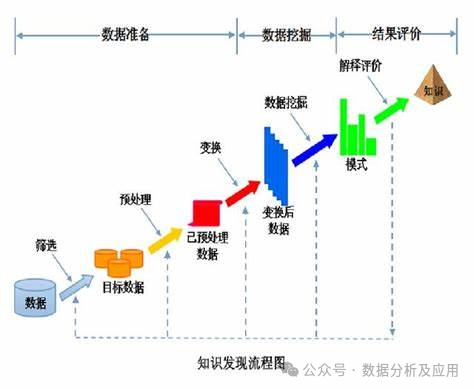
首先，進(jìn)行數(shù)據(jù)挖掘的第一步是數(shù)據(jù)選擇。在明確了業(yè)務(wù)需求后，我們需要從各種來源中選擇與需求相關(guān)的數(shù)據(jù)。這些數(shù)據(jù)可能來自業(yè)務(wù)原始數(shù)據(jù)、公開的數(shù)據(jù)集，或者通過爬蟲從網(wǎng)站上抓取的結(jié)構(gòu)化數(shù)據(jù)。選擇合適的數(shù)據(jù)是進(jìn)行數(shù)據(jù)挖掘的基礎(chǔ)。
接下來是數(shù)據(jù)預(yù)處理階段。在這個階段，我們需要對選定的數(shù)據(jù)進(jìn)行清洗和處理，以消除其中的噪音和不完整信息。
完成數(shù)據(jù)預(yù)處理后，我們進(jìn)入特征工程或數(shù)據(jù)轉(zhuǎn)換階段。這個階段的目標(biāo)是根據(jù)所選擇的算法，從預(yù)處理好的數(shù)據(jù)中提取出有意義的特征，并將其轉(zhuǎn)換為適合特定數(shù)據(jù)挖掘算法的分析模型。
然后是數(shù)據(jù)挖掘階段。在這個階段，我們將使用選定的數(shù)據(jù)挖掘算法對處理過的數(shù)據(jù)進(jìn)行深入分析，以發(fā)現(xiàn)其中的模式和關(guān)聯(lián)。
最后是解釋與評價階段。在這個階段，我們將對數(shù)據(jù)挖掘的結(jié)果進(jìn)行解釋和評價，以便將其應(yīng)用于實際的工作領(lǐng)域。

二、數(shù)據(jù)挖掘算法簡介

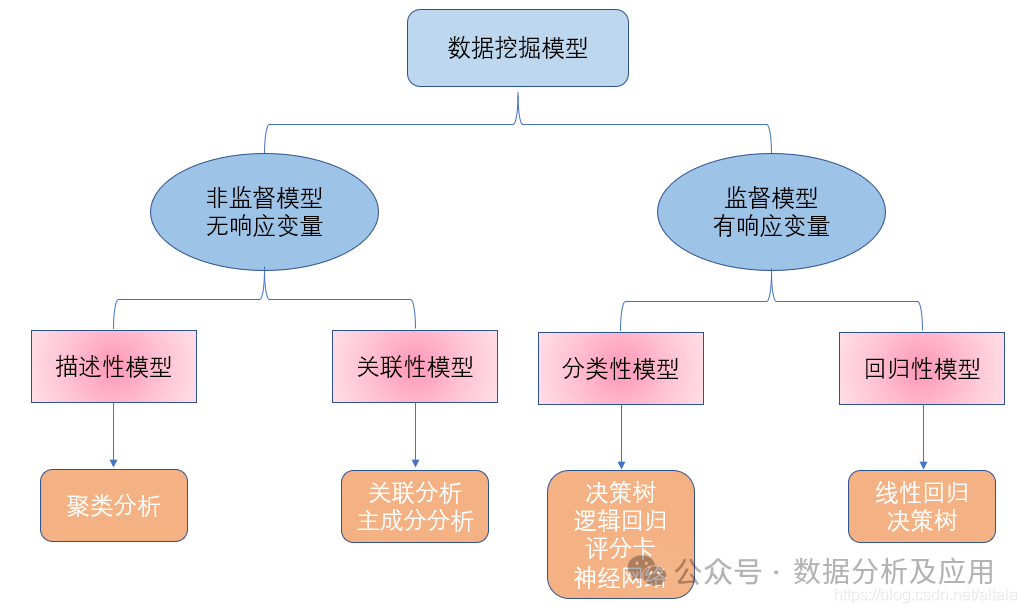
2.1 關(guān)聯(lián)分析
關(guān)聯(lián)規(guī)則分析的目標(biāo)是發(fā)現(xiàn)數(shù)據(jù)集中不同屬性之間的關(guān)聯(lián)。為了達(dá)到這個目標(biāo)，關(guān)聯(lián)規(guī)則算法設(shè)置了最小支持度閾值和最小置信度閾值。這些算法致力于在盡可能高效的方式下完成這個任務(wù)。

常見的關(guān)聯(lián)規(guī)則算法包括Apriori算法、AprioriTid算法和FP-growth算法。

2.2 分類算法
分類算法的目標(biāo)是將數(shù)據(jù)集中的對象分配到預(yù)定義的類別中。以下是幾種經(jīng)典的分類算法：

決策樹算法：使用樹形結(jié)構(gòu)表示分類或決策集合，從而產(chǎn)生規(guī)則或發(fā)現(xiàn)規(guī)律。主要的算法包括ID3、C4.5、SLIQ、SPRING和RainForest。
樸素貝葉斯分類算法：基于貝葉斯定理，通過計算每個類別的概率來選擇概率最大的類別進(jìn)行分類。
KNN分類算法：基于最近鄰原理，將距離相近的歸為同一類。
CBA（基于關(guān)聯(lián)規(guī)則的分類算法）：利用關(guān)聯(lián)規(guī)則進(jìn)行分類。
MIND（在數(shù)據(jù)庫中挖掘）算法：使用用戶定義的函數(shù)（UDF）在數(shù)據(jù)庫中實現(xiàn)分類的算法。
神經(jīng)網(wǎng)絡(luò)分類算法：利用訓(xùn)練集對多層的神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，然后用訓(xùn)練好的模型對樣本進(jìn)行分類。
粗集理論：一種不需要預(yù)先給出特征或?qū)傩詳?shù)量描述的分類方法，直接從問題出發(fā)，通過不可分辨關(guān)系和不可分辨類確定近似域，找出問題的內(nèi)在規(guī)律。
遺傳算法：模擬生物進(jìn)化過程的優(yōu)化求解技術(shù)，利用選擇、交叉和變異三個基本方法進(jìn)行優(yōu)化。

2.3 回歸分析

回歸分析主要研究因變量（目標(biāo)）和自變量（預(yù)測器）之間的關(guān)系。在大數(shù)據(jù)分析中，回歸分析是一種預(yù)測性的建模技術(shù)，它通過研究因變量和影響它的自變量之間的回歸模型，來預(yù)測因變量的發(fā)展趨勢。當(dāng)有多個自變量時，可以研究每個自變量對因變量的影響強度。

回歸分析的分類如下：

按自變量的多少分為：一元回歸分析和多元回歸分析。
按因變量的多少分為：簡單回歸分析和多重回歸分析。
按自變量和因變量之間的相關(guān)關(guān)系不同分為：線性回歸分析和非線性回歸分析。

2.4 聚類算法
聚類分析處理的對象集合中，對象的類是未知的。它的目標(biāo)是將對象集合分組為多個由類似對象組成的簇。聚類分析的方法可以分為以下三類：

分區(qū)方法：給定一個包含N個對象或元組的數(shù)據(jù)庫，分區(qū)方法構(gòu)建數(shù)據(jù)的K個劃分，每個劃分表示一個聚簇，且K < N。經(jīng)典算法是K-MEAN（K平均值）算法。
層次方法：對給定的數(shù)據(jù)對象集合進(jìn)行層次的分解。經(jīng)典算法是BIRCH（平衡迭代減少和聚類使用層次結(jié)構(gòu)）算法。
基于網(wǎng)格的方法：采用多分辨率的網(wǎng)格數(shù)據(jù)結(jié)構(gòu)，將空間量化為有限數(shù)目的單元，形成網(wǎng)格結(jié)構(gòu)，所有的聚類分析都在網(wǎng)格上進(jìn)行。常用的算法有STING（統(tǒng)計信息網(wǎng)格）、CLIQUE（基于網(wǎng)格的聚類）和SKWAVECLUSTER（聲波聚類）等。

三、相關(guān)預(yù)備知識

3.1 距離（相似度）度量

距離度量可用于在數(shù)據(jù)挖掘中明確樣本數(shù)據(jù)相似度，通常可以計算樣本間的距離，如下為常用距離度量的介紹。

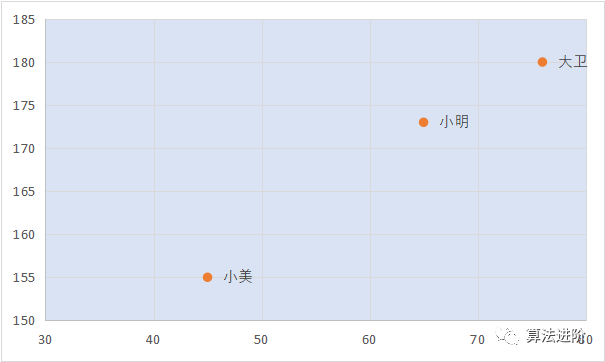
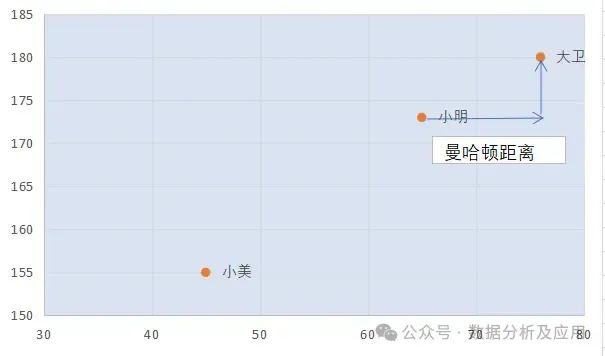
樣本數(shù)據(jù)以如下三個人的身高體重示例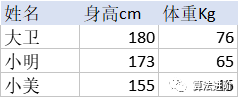：展示到坐標(biāo)圖中是這樣的：

曼哈頓距離： 也稱曼哈頓街區(qū)距離，就如從街區(qū)的一個十字路口點到另一個十字路口點的距離，二維空間（多維空間按同理擴展）用公式表示為

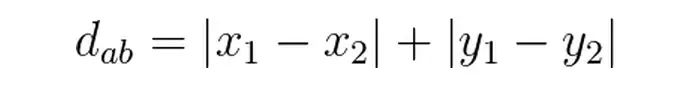
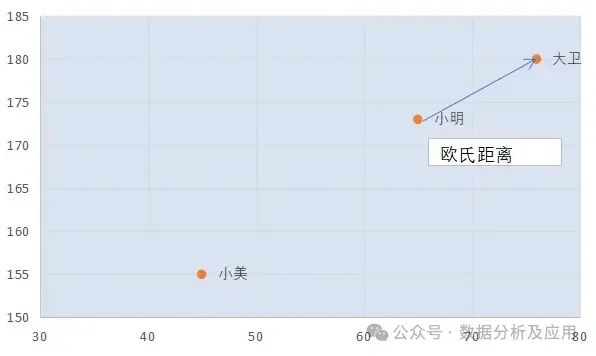
歐氏距離：表示為點到點的距離。二維空間（多維空間按同理擴展）的公式表示為

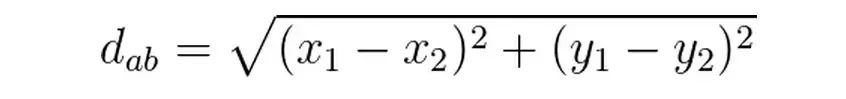
閔可夫斯基距離：其實就是距離方法的通用概括，當(dāng) p=1 既是曼哈頓距離，當(dāng) p=2 既是歐氏距離。當(dāng)p越大，單一維度的差值對整體的影響就越大。

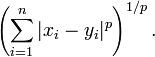
余弦相關(guān)系數(shù)：

樣本數(shù)據(jù)視為向量，通過兩向量間的夾角余弦值確認(rèn)相關(guān)性，數(shù)值范圍[-1，1]。-1表示負(fù)相關(guān)，0表示無關(guān)，1表示正相關(guān)。

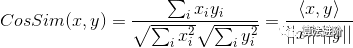余弦相關(guān)系數(shù)的優(yōu)缺點：

優(yōu)點：余弦相似度與向量的幅值無關(guān)，只與向量的方向相關(guān)，在文檔相似度（TF-IDF）和圖片相似性（histogram）計算上都有它的身影；而且在樣本數(shù)值稀疏的時候仍可以使用。

缺點：余弦相似度受到向量的平移影響，上式如果將 x 平移到 x+1, 余弦值就會改變。(可以理解為受樣本的起始標(biāo)準(zhǔn)的影響，接下來介紹的皮爾遜相關(guān)系數(shù)可以消除這個影響)

皮爾遜相關(guān)系數(shù)：

計算出了樣本向量間的相關(guān)性，數(shù)值范圍[-1，1]。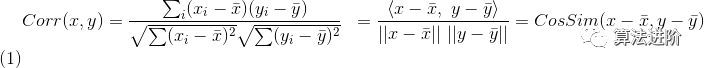

考慮計算的遍歷的次數(shù)，有一個替代公式可以近似計算皮爾遜相關(guān)系數(shù)：

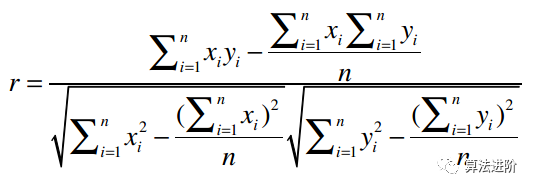
皮爾遜相關(guān)系數(shù)優(yōu)點：可消除每個分量標(biāo)準(zhǔn)不同（分?jǐn)?shù)膨脹）的影響，具有平移不變性和尺度不變性。

3.2 數(shù)據(jù)標(biāo)準(zhǔn)化

數(shù)據(jù)中如果各分量的單位尺度差異很大，可以使用數(shù)據(jù)標(biāo)準(zhǔn)化消除不同分量間單位尺度的影響，，加速模型收斂的效率，常用的方法有三種：

min-max 標(biāo)準(zhǔn)化：將數(shù)值范圍縮放到（0,1）,但沒有改變數(shù)據(jù)分布。max為樣本最大值，min為樣本最小值。

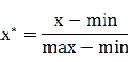
z-score 標(biāo)準(zhǔn)化：將數(shù)值范圍縮放到0附近, 經(jīng)過處理的數(shù)據(jù)符合標(biāo)準(zhǔn)正態(tài)分布。u是平均值，σ是標(biāo)準(zhǔn)差。

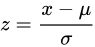
修正的標(biāo)準(zhǔn)z-score：修正后可以減少樣本數(shù)據(jù)異常值的影響。將z-score標(biāo)準(zhǔn)化公式中的均值改為中位數(shù)，將標(biāo)準(zhǔn)差改為絕對偏差。

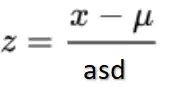
其中asd絕對偏差：u為中位數(shù)，card(x)為樣本個數(shù)

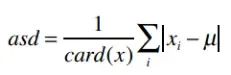
3.3 算法的效果評估方法

十折交叉驗證：將數(shù)據(jù)集隨機分成十份，每次使用九份進(jìn)行訓(xùn)練，剩余一份進(jìn)行測試，這個過程重復(fù)十次，確保每份數(shù)據(jù)都至少被使用過一次作為測試集。關(guān)鍵在于保證數(shù)據(jù)集被均勻地分成十份。
N折交叉驗證：又稱為留一法，它利用幾乎所有的數(shù)據(jù)來進(jìn)行訓(xùn)練，然后留出一份數(shù)據(jù)進(jìn)行測試。這個過程會迭代進(jìn)行，確保每一份數(shù)據(jù)都被用作過測試集。
訓(xùn)練-測試劃分驗證：隨機將數(shù)據(jù)集劃分為訓(xùn)練集和驗證集，用于評估模型的性能。

四、數(shù)據(jù)挖掘算法原理及實踐

4.1 Apriori關(guān)聯(lián)分析算法

模型原理：Apriori算法是一種用于頻繁項集挖掘和關(guān)聯(lián)規(guī)則學(xué)習(xí)的算法。其主要思想是通過候選生成和剪枝策略發(fā)現(xiàn)頻繁項集。它利用了數(shù)據(jù)集中的項集（items）的先驗知識，通過減少不必要的搜索來提高效率。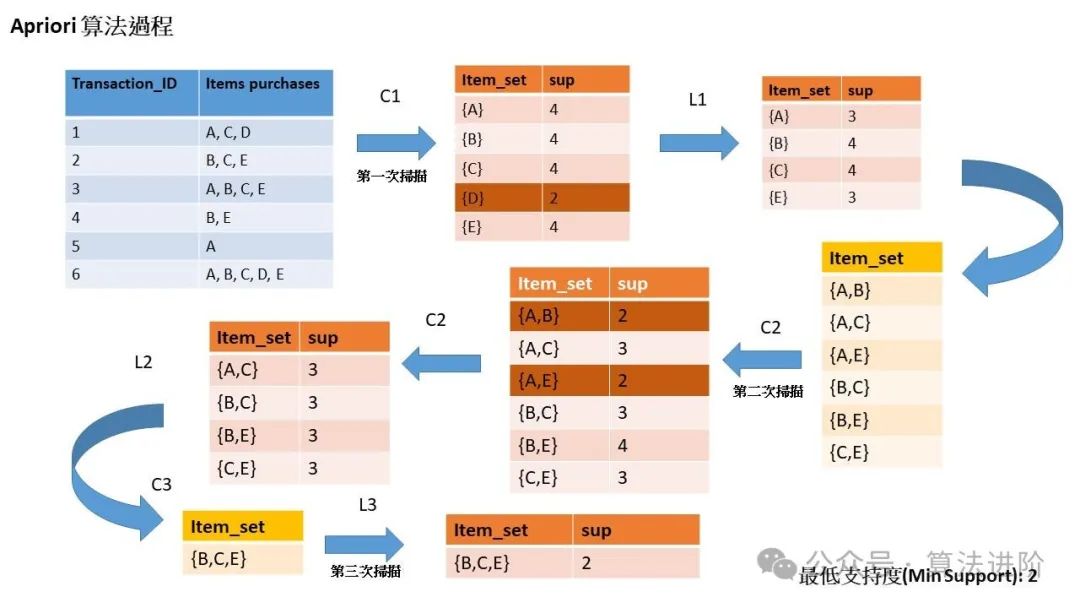

使用場景：常用于市場籃子分析，如超市購物籃分析，以發(fā)現(xiàn)商品之間的關(guān)聯(lián)關(guān)系。

Python示例代碼：


              
                from mlxtend.frequent_patterns import apriori  
              
              
                from mlxtend.frequent_patterns import association_rules  
              
              
                
                  

              
              
                
                  # 假設(shè)df是包含交易數(shù)據(jù)的DataFrame，'item'是商品列  
                
              
              
                frequent_itemsets = apriori(df, min_support=0.05, use_colnames=True)  
              
              
                rules = association_rules(frequent_itemsets, metric="confidence",min_threshold=0.7)

4.2 協(xié)同過濾推薦算法

基于用戶的協(xié)同過濾是通過計算用戶之間的距離找出最相似的用戶（需要將所有的評價數(shù)據(jù)在讀取在內(nèi)存中處理進(jìn)行推薦），并將相似用戶評價過的物品推薦給目標(biāo)用戶。

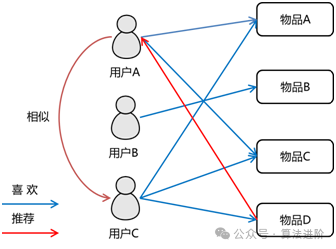
而基于物品的協(xié)同過濾則是找出最相似的物品（通過構(gòu)建一個物品的相似度模型來做推薦），再結(jié)合用戶的評價來給出推薦結(jié)果。算法常用有修正余弦相似度算法：以物品的評分作為物品的屬性值，通過對比物品i,j的共有的用戶相對評分的計算相關(guān)性s(i,j)。

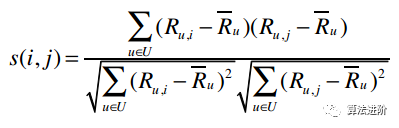
Python示例代碼：

          
            import numpy as np  
          
          
            
              

          
          
            
              # 用戶-物品評分矩陣  
            
          
          
            ratings = np.array([[5, 3, 0, 1],  
          
          
                               [4, 0, 0, 0],  
          
          
                               [0, 5, 3, 0],  
          
          
                               [0, 4, 5, 5]])  
          
          
            
              

          
          
            
              # 計算用戶之間的相似度  
            
          
          
            
              def similarity(ratings):
            
          
          
                n = ratings.shape[0]  
          
          
                sim = np.zeros((n, n))  
          
          
            for i in range(n):  
          
          
            for j in range(n):  
          
          
            if i != j:  
          
          
                            sim[i][j] = np.corrcoef(ratings[i], ratings[j])[0, 1]  
          
          
            return sim  
          
          
            
              

          
          
            
              # 基于用戶的協(xié)同過濾推薦算法  
            
          
          
            
              def user_based_collaborative_filtering(ratings, threshold=0.6):
            
          
          
                n = ratings.shape[0]  
          
          
                sim = similarity(ratings)  
          
          
                rec_list = {}  
          
          
            for i in range(n):  
          
          
            for j in range(n):  
          
          
            if i != j and sim[i][j] > threshold:  
          
          
            for k in range(len(ratings[j])):  
          
          
            if ratings[j][k] == 0 and ratings[i][k] != 0:  
          
          
                                    rec_list[k] = ratings[i][k]  
          
          
            return rec_list  
          
          
            
              

          
          
            
              # 獲取推薦結(jié)果  
            
          
          
            rec_list = user_based_collaborative_filtering(ratings)  
          
          
            print(rec_list)

4.3 分類算法

(1)基于物品特征值的KNN分類算法

代碼實現(xiàn)：iris鳶尾花KNN分類算法

          
            ...
          
          
            
              

          
          
             # KNN核心邏輯手寫
          
          
            def knn(self, oj_list):
          
          
            weight_dict = {"Iris-setosa":0.0, "Iris-versicolor":0.0, "Iris-virginica":0.0}
          
          
            for atuple in oj_list:
          
          
            weight_dict[atuple[1]] += (1.0 / atuple[0])
          
          
            rel_class = [(key, value) for key, value in weight_dict.items()]
          
          
            #print(sorted(rel_class, key=lambda x:x[1], reverse=True))
          
          
            rel_class = sorted(rel_class, key=lambda x:x[1], reverse=True)[0][0]
          
          
            return rel_class
          
          
            
              

          
          
            ...
          
          
            # 調(diào)用sklearn直接實現(xiàn)
          
          
            from sklearn.datasets import load_iris  
          
          
            from sklearn.model_selection import train_test_split  
          
          
            from sklearn.neighbors import KNeighborsClassifier  
          
          
            from sklearn.metrics import classification_report, confusion_matrix  
          
          
            
              

          
          
            # 加載鳶尾花數(shù)據(jù)集  
          
          
            iris = load_iris()  
          
          
            X = iris.data  
          
          
            y = iris.target  
          
          
            
              

          
          
            # 劃分?jǐn)?shù)據(jù)集為訓(xùn)練集和測試集  
          
          
            X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
          
          
            
              

          
          
            # 創(chuàng)建KNN分類器，并設(shè)置鄰居數(shù)量為3  
          
          
            knn = KNeighborsClassifier(n_neighbors=3)  
          
          
            
              

          
          
            # 使用訓(xùn)練數(shù)據(jù)訓(xùn)練KNN分類器  
          
          
            knn.fit(X_train, y_train)  
          
          
            
              

          
          
            # 使用測試數(shù)據(jù)進(jìn)行預(yù)測  
          
          
            y_pred = knn.predict(X_test)  
          
          
            
              

          
          
            # 輸出分類器的評估結(jié)果  
          
          
            print("Classification Report:\n", classification_report(y_test, y_pred))  
          
          
            print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))

前面我們討論的協(xié)同推薦算法，需要在用戶生成的各種數(shù)據(jù)上進(jìn)行深入分析，因此也被稱為社會化過濾算法。然而，這種算法存在一些明顯的問題，如數(shù)據(jù)的稀疏性、算法的可擴展性，以及過度依賴用戶數(shù)據(jù)。為了解決這些問題，我們可以采用基于物品特征值分類的算法。

這個算法主要分為兩個步驟：第一步是特征值的選取。這一步是至關(guān)重要的，因為它決定了算法的準(zhǔn)確性和效率。我們需要挑選出具有代表性且能提供區(qū)分度的特征值。以Iris花為例，我們可以選取花萼長度、花萼寬度、花瓣長度和花瓣寬度作為特征值。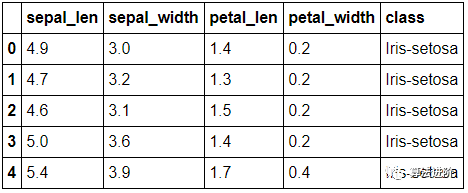

第二步是計算距離。在這一步中，我們將測試集與訓(xùn)練集的特征值進(jìn)行比較，計算它們之間的曼哈頓距離。通過這種方式，我們可以找到與測試集最相似的k個訓(xùn)練樣本。然后，我們使用加權(quán)后的結(jié)果來預(yù)測分類。
然而，KNN分類算法也存在一些缺點。首先，它無法對分類結(jié)果的置信度進(jìn)行量化，這意味著我們無法確定分類的準(zhǔn)確性。其次，它是一種被動學(xué)習(xí)的算法，這意味著每次進(jìn)行測試時都需要遍歷所有的訓(xùn)練集，這可能導(dǎo)致算法的效率較低。

(2)貝葉斯分類算法

代碼實現(xiàn)：

          
            ...
          
          
            
              # bayes 核心邏輯手寫
            
          
          
            
              def bayes(self):
            
          
          
            
              #訓(xùn)練組的條件概率
            
          
          
            for word in self.vocabulary:
          
          
            for category,value in self.prob.items():
          
          
            if word not in self.prob[category]:
          
          
            count = 0
          
          
            else :
          
          
            count = self.prob[category][word]
          
          
            
              #優(yōu)化條件概率公式
            
          
          
            self.prob[category][word] = (count + 1) / (self.total[category] + len(self.vocabulary)) 
          
          
            
              

          
          
            ...
          
          
            
              # 調(diào)用sklearn實現(xiàn)
            
          
          
            from sklearn.feature_extraction.text import CountVectorizer  
          
          
            from sklearn.naive_bayes import MultinomialNB  
          
          
            from sklearn.model_selection import train_test_split  
          
          
            from sklearn.metrics import accuracy_score  
          
          
            import pandas as pd  
          
          
            
              

          
          
            
              # 假設(shè)你有一個文本數(shù)據(jù)集，存儲在CSV文件中，有兩列：'text'和'label'  
            
          
          
            data = pd.read_csv('text_data.csv')  
          
          
            
              

          
          
            
              # 提取特征和標(biāo)簽  
            
          
          
            X = data['text'].values  
          
          
            y = data['label'].values  
          
          
            
              

          
          
            
              # 切分?jǐn)?shù)據(jù)集為訓(xùn)練集和測試集  
            
          
          
            X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  
          
          
            
              

          
          
            
              # 使用CountVectorizer將文本轉(zhuǎn)換為向量  
            
          
          
            vectorizer = CountVectorizer()  
          
          
            X_train_transformed = vectorizer.fit_transform(X_train)  
          
          
            X_test_transformed = vectorizer.transform(X_test)  
          
          
            
              

          
          
            
              # 使用樸素貝葉斯分類器進(jìn)行訓(xùn)練  
            
          
          
            classifier = MultinomialNB()  
          
          
            classifier.fit(X_train_transformed, y_train)  
          
          
            
              

          
          
            
              # 對測試集進(jìn)行預(yù)測  
            
          
          
            y_pred = classifier.predict(X_test_transformed)  
          
          
            
              

          
          
            
              # 計算準(zhǔn)確率  
            
          
          
            accuracy = accuracy_score(y_test, y_pred)  
          
          
            print(f"Accuracy: {accuracy}")

貝葉斯分類算法是基于概率的分類算法。相比于KNN分類算法，它是主動學(xué)習(xí)的算法，它會根據(jù)訓(xùn)練集建立一個模型，并用這個模型對新樣本進(jìn)行分類，速度也會快很多。

貝葉斯分類算法的理論基礎(chǔ)是基于條件概率的公式（應(yīng)用于現(xiàn)實中P(X|Y&Z)不直觀得出，而P(Y|X)*P(Z|X)比較直觀得出），并假設(shè)已存在的子事件(y,z...實際應(yīng)用中會有多個)間是相互獨立的（因此也稱為樸素貝葉斯），當(dāng)y，z事件假設(shè)為獨立便有：

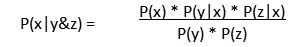
如下舉例推測買牛奶和有機食品，再會買綠茶的概率：

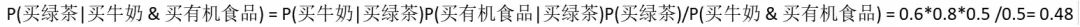
第一步：計算先驗概率及條件概率

先驗概率：為單獨事件發(fā)生的概率，如P(買綠茶)，P(有機食品)

條件概率（后驗概率）：y事件已經(jīng)發(fā)生，觀察y數(shù)據(jù)集后得出x發(fā)生的概率。如P(買有機食品|買綠茶)，通過以下公式計算（nc表示y數(shù)據(jù)集下x的發(fā)生頻數(shù)，n為y數(shù)據(jù)集的總數(shù)）：

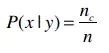
上式存在一個缺陷，當(dāng)一個條件概率 P(y|x)為0時，整體的預(yù)測結(jié)果P(x) * P(y|x) * P(z|x)只能為0，這樣便不能更全面地預(yù)測。

修正后的條件概率：（公式摘自Tom Mitchell《機器學(xué)習(xí)》。m是一個常數(shù)，表示等效樣本大小。決定常數(shù)m的方法有很多，我們這里可以使用預(yù)測結(jié)果的類別來作為m，比如投票有贊成和否決兩種類別，所以m就為2。p則是相應(yīng)的先驗概率，比如說贊成概率是0.5，那p(贊成)就是0.5。）：

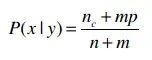
第二歩：根據(jù)貝葉斯公式做出預(yù)測

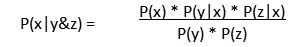
由公式計算比較y&z事件發(fā)生下，不同x事件發(fā)生的概率差異，如得出P（x=喜歡），P（x=不喜歡）的概率大小，預(yù)測為概率比較大的事件。因為P(y)*p(z)在上式都一樣，因此公式可以簡化為計算概率最大項而預(yù)測分類：

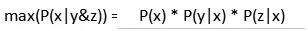
貝葉斯算法的優(yōu)點：能夠給出分類結(jié)果的置信度；它是一種主動學(xué)習(xí)算法，速度更快。

貝葉斯算法的缺點：需要特定格式；數(shù)值型數(shù)據(jù)需要轉(zhuǎn)換為類別計算概率或用高斯分布計算概率；

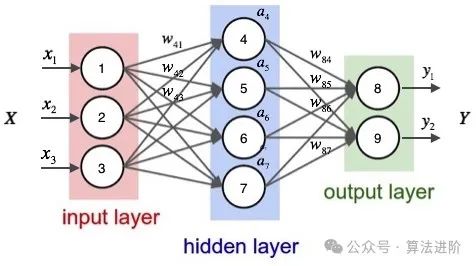
(3)神經(jīng)網(wǎng)絡(luò)(DNN)分類算法

代碼實現(xiàn) ：

          
            
              import tensorflow as tf  
            
          
          
            
              from tensorflow.keras import layers, models  
            
          
          
            
              import numpy as np  
            
          
          
            
              import matplotlib.pyplot as plt  
            
          
          
            
              import cv2  
            
          
          
            
              

          
          
            
              # 加載數(shù)據(jù)集，這里我們使用的是MNIST數(shù)據(jù)集，你可以替換成自己的數(shù)據(jù)集  
            
          
          
            
              (train_images, train_labels), (test_images, test_labels) = tf.keras.datasets.mnist.load_data()  
            
          
          
            
              

          
          
            
              # 對數(shù)據(jù)進(jìn)行歸一化處理  
            
          
          
            
              train_images = train_images / 255.0
            
          
          
            
              test_images = test_images / 255.0
            
          
          
            
              

          
          
            
              # 構(gòu)建DNN模型  
            
          
          
            
              model = models.Sequential()  
            
          
          
            
              model.add(layers.Dense(512, activation='sigmoid', input_shape=(28, 28)))  # 輸入層，28x28是MNIST圖片的大小  
            
          
          
            
              model.add(layers.Dense(512, activation='sigmoid'))  # 隱藏層  
            
          
          
            
              model.add(layers.Dense(10, activation='softmax'))  # 輸出層，10個類別，使用softmax激活函數(shù)進(jìn)行多分類  
            
          
          
            
              

          
          
            
              # 編譯模型，設(shè)置損失函數(shù)、優(yōu)化器和評估指標(biāo)  
            
          
          
            
              model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])  
            
          
          
            
              

          
          
            
              # 訓(xùn)練模型  
            
          
          
            
              model.fit(train_images, train_labels, epochs=5)  
            
          
          
            
              

          
          
            
              # 在測試集上評估模型性能  
            
          
          
            
              test_loss, test_acc = model.evaluate(test_images, test_labels)  
            
          
          
            
              print('\nTest accuracy:', test_acc)  
            
          
          
            
              

          
          
            
              # 使用模型進(jìn)行預(yù)測并可視化結(jié)果  
            
          
          
            
              predictions = model.predict(test_images)  
            
          
          
            
              predicted_class = np.argmax(predictions, axis=1)  # 獲取預(yù)測類別  
            
          
          
            
              true_class = np.argmax(test_labels, axis=1)  # 獲取真實類別  
            
          
          
            
              plt.figure(figsize=(10, 5))  
            
          
          
            
              for i in range(len(test_images)):  
            
          
          
            
                  plt.subplot(1, 2, i+1)  
            
          
          
            
                  plt.imshow(test_images[i].reshape(28, 28), cmap='gray')  
            
          
          
            
                  plt.title('Predicted: ' + str(predicted_class[i]) + ', True: ' + str(true_class[i]))  
            
          
          
            
              plt.show()

DNN分類算法實現(xiàn)了輸入圖片特征向量X，輸出Y（范圍0~1）預(yù)測X的分類。

第一步，得到關(guān)于X線性回歸函數(shù)

可以通過線性回歸得到WX + b，其中W是權(quán)重，b是偏差值。但不能用本式表述預(yù)測的值，因為輸出Y的值需要在（0~1）區(qū)間；

第二歩，通過激活函數(shù)轉(zhuǎn)換

激活函數(shù)的特點是可以將線性函數(shù)轉(zhuǎn)換為非線性函數(shù)，并且有輸出值有限，可微分，單調(diào)性的特點。本例使用sigmoid，使輸出為預(yù)測值Y=sigmoid（WX+b）；

多個神經(jīng)網(wǎng)絡(luò)層，也就是重復(fù)第一、二步，類似sigmoid(sigmoid（WX+b）)..的復(fù)合函數(shù)。

第三歩，構(gòu)建Cost函數(shù)

訓(xùn)練W，b更好的預(yù)測真實的類別需要構(gòu)建Cost代價函數(shù)，y^為sigmoid(WX+b)的預(yù)測分類值，y為實際分類值（0或者1）：

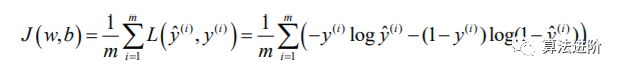
其中L(y^,y)稱為損失函數(shù) 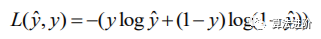訓(xùn)練的目的就是為了讓L(y^,y)足夠小，也就是當(dāng)y實際分類值為1時，y^要盡量偏向1。y實際分類值為0時，y^盡量小接近0。

第四步，梯度下降得到Cost函數(shù)的極小值

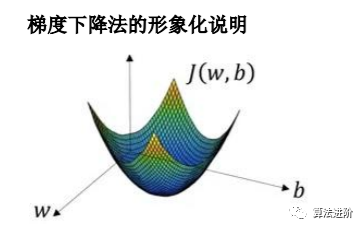通過對W,b兩個參數(shù)求偏導(dǎo)，不斷迭代往下坡的的位置移動（對w，b值往極小值方向做優(yōu)化，其中α為學(xué)習(xí)率控制下降的幅度），全局最優(yōu)解也就是代價函數(shù)（成本函數(shù)）J (w,b)這個凸函數(shù)的極小值點。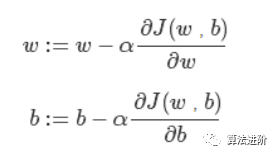第五步、通過訓(xùn)練好的W,b預(yù)測分類。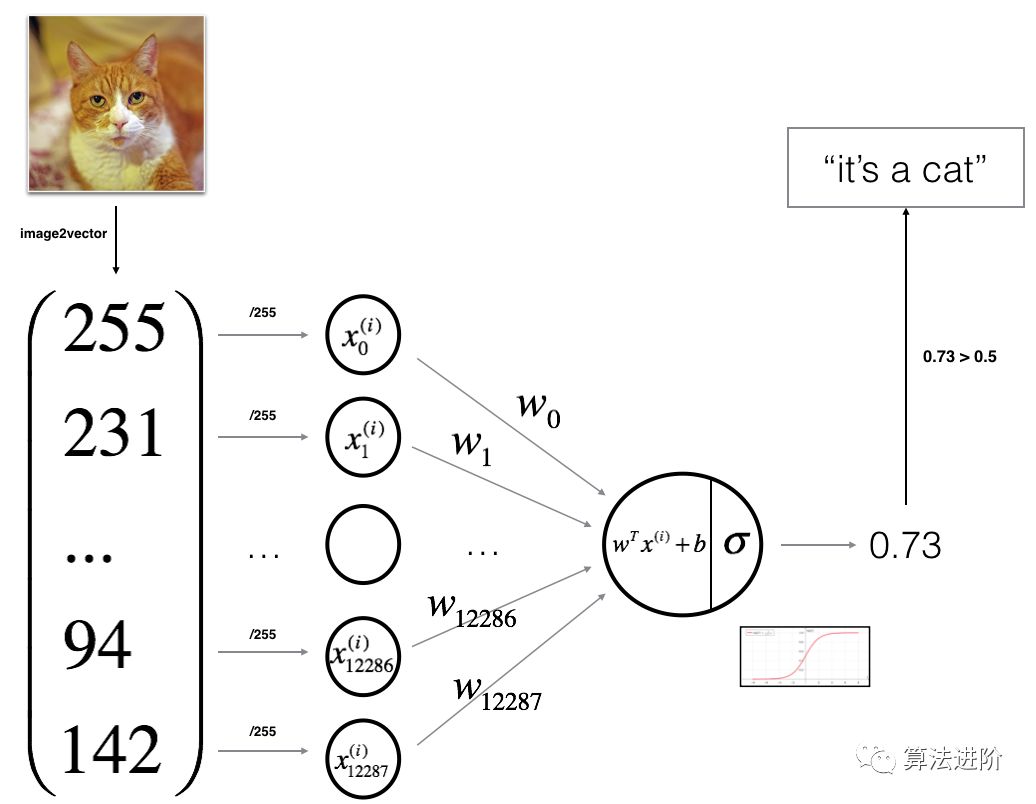

4.4 聚類算法

(1)層次聚類

層次聚類將每條數(shù)據(jù)都當(dāng)作是一個分類，每次迭代的時候合并距離最近的兩個分類，直到剩下一個分類為止。

代碼實現(xiàn)：

          
            from sklearn.cluster import AgglomerativeClustering  
          
          
            from sklearn.datasets import make_blobs  
          
          
            import matplotlib.pyplot as plt  
          
          
            
              

          
          
            
              # 生成樣本數(shù)據(jù)  
            
          
          
            X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)  
          
          
            
              

          
          
            
              # 實例化層次聚類模型，n_clusters為聚類數(shù)  
            
          
          
            cluster = AgglomerativeClustering(n_clusters=4)  
          
          
            
              

          
          
            
              # 擬合數(shù)據(jù)  
            
          
          
            cluster.fit(X)  
          
          
            
              

          
          
            
              # 獲取聚類標(biāo)簽  
            
          
          
            labels = cluster.labels_  
          
          
            
              

          
          
            
              # 繪制結(jié)果  
            
          
          
            plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  
          
          
            plt.show()

(2)K-means++聚類

注：Kmean算法與Kmean++區(qū)別在于初始的中心點是直接隨機選取k各點。

代碼實現(xiàn)：

          
            from sklearn.cluster import KMeans  
          
          
            from sklearn import datasets  
          
          
            import matplotlib.pyplot as plt  
          
          
            
              

          
          
            
              # 加載Iris數(shù)據(jù)集  
            
          
          
            iris = datasets.load_iris()  
          
          
            X = iris.data  
          
          
            y = iris.target  
          
          
            
              

          
          
            
              # 創(chuàng)建KMeans實例并擬合數(shù)據(jù)  
            
          
          
            kmeans = KMeans(n_clusters=3)  
          
          
            kmeans.fit(X)  
          
          
            
              

          
          
            
              # 獲取聚類標(biāo)簽和聚類中心點  
            
          
          
            labels = kmeans.labels_  
          
          
            centroids = kmeans.cluster_centers_  
          
          
            
              

          
          
            
              # 繪制聚類結(jié)果  
            
          
          
            
              plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')  
            
          
          
            
              plt.scatter(centroids[:, 0], centroids[:, 1], c='red', s=300)  # 繪制聚類中心點  
            
          
          
            plt.show()

k-means++算法可概括為：

（1）基于各點到中心點得距離分量，依次隨機選取到k個元素作為中心點：先隨機選擇一個點。重復(fù)以下步驟，直到選完k個點。

計算每個數(shù)據(jù)點dp(n)到各個中心點的距離（D），選取最小的值D(dp)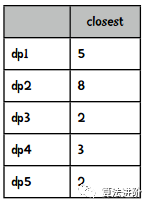；根據(jù)D(dp)距離所占的份量來隨機選取下一個點作為中心點。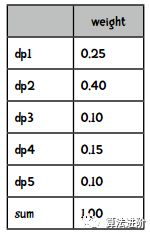

（2）根據(jù)各點到中心點的距離分類；

（3）計算各個分類新的中心點。重復(fù)(2、3)，直至滿足條件。

Python數(shù)據(jù)挖掘算法入門與實踐

二、數(shù)據(jù)挖掘算法簡介

三、相關(guān)預(yù)備知識

3.1 距離（相似度）度量

距離度量可用于在數(shù)據(jù)挖掘中明確樣本數(shù)據(jù)相似度，通常可以計算樣本間的距離，如下為常用距離度量的介紹。

3.2 數(shù)據(jù)標(biāo)準(zhǔn)化

3.3 算法的效果評估方法

四、數(shù)據(jù)挖掘算法原理及實踐

4.2 協(xié)同過濾推薦算法

4.3 分類算法

(1)基于物品特征值的KNN分類算法

代碼實現(xiàn)：iris鳶尾花KNN分類算法

(2)貝葉斯分類算法

代碼實現(xiàn)：

(3)神經(jīng)網(wǎng)絡(luò)(DNN)分類算法

代碼實現(xiàn) ：

4.4 聚類算法

(1)層次聚類

層次聚類將每條數(shù)據(jù)都 當(dāng)作是一個分類，每次迭代的時候合并距離最近的兩個分類，直到剩下一個分類為止。

代碼實現(xiàn)：

(2)K-means++聚類

代碼實現(xiàn)：

層次聚類將每條數(shù)據(jù)都當(dāng)作是一個分類，每次迭代的時候合并距離最近的兩個分類，直到剩下一個分類為止。