一個(gè)破堆排我搞了 4 個(gè)動(dòng)畫(huà)?
在小屋點(diǎn)擊刷題小隊(duì)
加入每天用小程序打卡的刷題小隊(duì)
今天咱們一起來(lái)看看這個(gè)賊有意思的堆排序。
說(shuō)堆排序之前,我們先簡(jiǎn)單了解一些什么是堆?堆這種數(shù)據(jù)結(jié)構(gòu)應(yīng)用場(chǎng)景非常多,所以我們需要熟練掌握。
那我們了解堆之前,先來(lái)簡(jiǎn)單了解下,什么是完全二叉樹(shù)?
我們來(lái)看下百度百科的定義
完全二叉樹(shù):葉子結(jié)點(diǎn)只能出現(xiàn)在最下層和次下層,且最下層的葉子結(jié)點(diǎn)集中在樹(shù)的左部。
哦,這樣啊!我們也可以這樣理解,除了最后一層,其他層的節(jié)點(diǎn)個(gè)數(shù)都是滿的,而且最后一層的葉子節(jié)點(diǎn)必須靠左。
光看文字還是太抽象,我們通過(guò)幾個(gè)例子進(jìn)行描述
下面我們來(lái)看一下這幾個(gè)例子
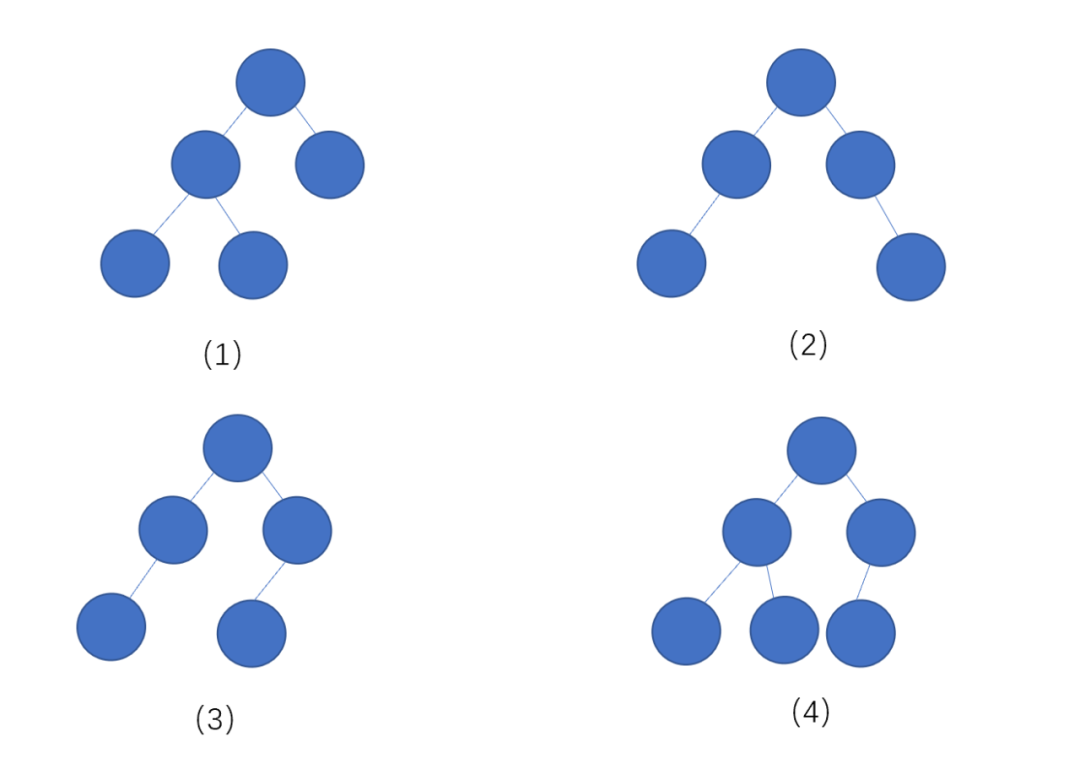
上面的幾個(gè)例子中,哪些是完全二叉樹(shù),哪些不是完全二叉樹(shù)?
根據(jù)定義可知(1)(4)為完全二叉樹(shù),(2)(3)不是完全二叉樹(shù),因?yàn)樗鼈?span style="color:rgb(62,62,62);font-family:'Helvetica Neue', Helvetica, 'Hiragino Sans GB', 'Microsoft YaHei', Arial, sans-serif;font-size:16px;">不符合最后一層的葉子節(jié)點(diǎn)必須在左邊。
通過(guò)上面的幾個(gè)例子,我們了解了什么是完全二叉樹(shù),
堆到底是什么呢?
下面我們來(lái)看一下二叉堆的要求
(1)必須是完全二叉樹(shù)
(2)二叉堆中的每一個(gè)節(jié)點(diǎn),都必須大于等于(或小于等于)其子樹(shù)中每個(gè)節(jié)點(diǎn)的值。
若是每個(gè)節(jié)點(diǎn)大于等于子樹(shù)中的每個(gè)節(jié)點(diǎn),我們稱之為大頂堆,小于等于子樹(shù)中的每個(gè)節(jié)點(diǎn),我們則稱之為小頂堆。
下面我們?cè)賮?lái)看一下二叉堆的具體例子。
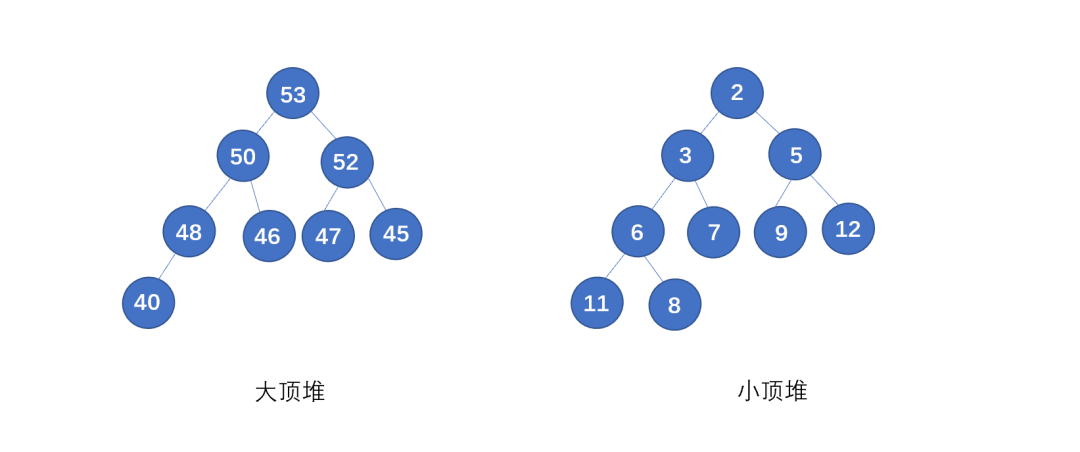 堆
堆上圖則為大頂堆和小頂堆,我們?cè)賮?lái)回顧一下堆的要求,看下是否符合
(1)必須是完全二叉樹(shù)
(2)堆中的每一個(gè)節(jié)點(diǎn),都必須大于等于(或小于等于)其子樹(shù)中每個(gè)節(jié)點(diǎn)的值。
好啦,到這里我們已經(jīng)完全掌握二叉堆了,那么二叉堆又是怎么存儲(chǔ)的呢?
因?yàn)槎咽峭耆鏄?shù),所以我們完全可以用數(shù)組存儲(chǔ)。具體思想見(jiàn)下圖,我們僅僅按照順序?qū)⒐?jié)點(diǎn)存入數(shù)組即可,我們通過(guò)小頂堆進(jìn)行演示。
注:我們這里是從下標(biāo) 1 開(kāi)始存儲(chǔ)的,更加直觀,下文中我們將二叉堆簡(jiǎn)稱為堆
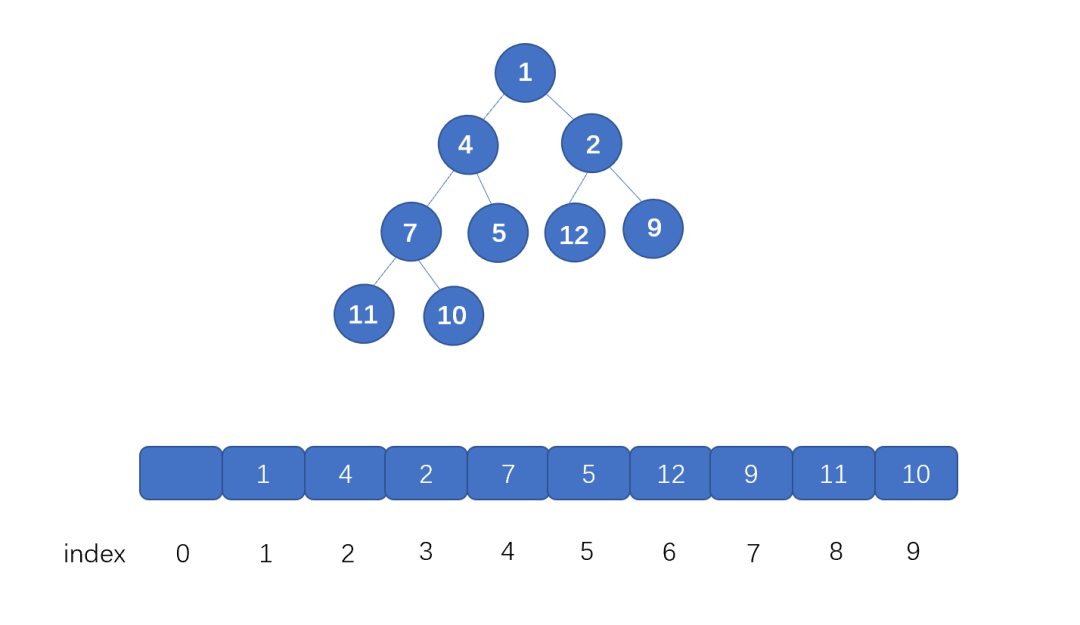
我們來(lái)看一下為什么我們可以用數(shù)組來(lái)存儲(chǔ)堆
我們首先看根節(jié)點(diǎn),也就是值為 1 的節(jié)點(diǎn),它在數(shù)組中的下標(biāo)為 1 ,它的左子節(jié)點(diǎn),也就是值為 4 的節(jié)點(diǎn),此時(shí)索引為 2,右子節(jié)點(diǎn)也就是值為 2 的節(jié)點(diǎn),它的索引為 3。
我們發(fā)現(xiàn)其中的關(guān)系了嗎?
數(shù)組中,某節(jié)點(diǎn)(非葉子節(jié)點(diǎn))的下標(biāo)為 i , 那么其左子節(jié)點(diǎn)下標(biāo)為 2 *?i (這里可以直接通過(guò)相乘得到左孩子,如果從 0 開(kāi)始存,需要 2 *?i + 1 才行)
右子節(jié)點(diǎn)為 ?2*i+1,其父節(jié)點(diǎn)為 i / 2 。既然我們完全可以根據(jù)索引找到某節(jié)點(diǎn)的 左子節(jié)點(diǎn) 和 右子節(jié)點(diǎn),那么我們用數(shù)組存儲(chǔ)是完全沒(méi)有問(wèn)題的。
好啦,我們知道了什么是堆和如何用數(shù)組存儲(chǔ)堆,那我們?nèi)绾瓮瓿啥雅判蚰兀?/p>
堆排序其實(shí)主要有兩個(gè)步驟
建堆
排序
下面我們先來(lái)了解下建堆
我們剛才說(shuō)了用數(shù)組來(lái)存儲(chǔ)大頂(小頂)堆,此時(shí)的元素已經(jīng)滿足某節(jié)點(diǎn)大于等于(或小于等于)子樹(shù)節(jié)點(diǎn)。
但是隨機(jī)給我們一個(gè)數(shù)組,此時(shí)并不一定滿足上訴要求,所以我們需要調(diào)整數(shù)組,使其滿足大頂堆或小頂堆的要求。這個(gè)就是建堆,也可以稱其為堆化。
建堆我們這里提出兩種方法,利用上浮操作,也就是不斷插入元素進(jìn)行建堆,另一種是利用下沉操作,遍歷非葉子節(jié)點(diǎn),不斷將其下沉,進(jìn)行建堆,我們一起來(lái)看吧。
利用上浮操作建堆
說(shuō)之前我們先來(lái)了解下,如何往已經(jīng)建好的堆里,插入新的元素,我們直接看例子吧,一下就懂啦。
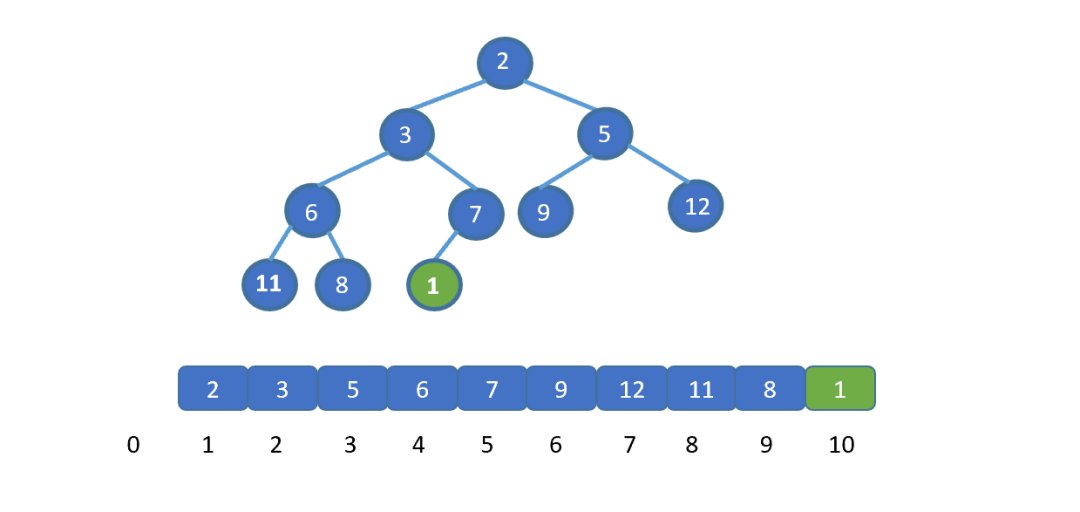 插入元素
插入元素假設(shè)讓我們插入新的元素 ?1 (綠色節(jié)點(diǎn)),我們發(fā)現(xiàn)此時(shí) 1 小于其父節(jié)點(diǎn) 的值 7 ,并不遵守小頂堆的規(guī)則,那我們則需要移動(dòng)元素 1 。讓 1 與 7 交換,(如果新插入元素大于父節(jié)點(diǎn)的值,則說(shuō)明插入新節(jié)點(diǎn)后仍滿足小頂堆規(guī)則,無(wú)需交換)。
之前我們說(shuō)過(guò),我們可以用數(shù)組保存堆,并且可以通過(guò) i/2 得到其父節(jié)點(diǎn)的值,那么此時(shí)我們就明白怎么做啦。
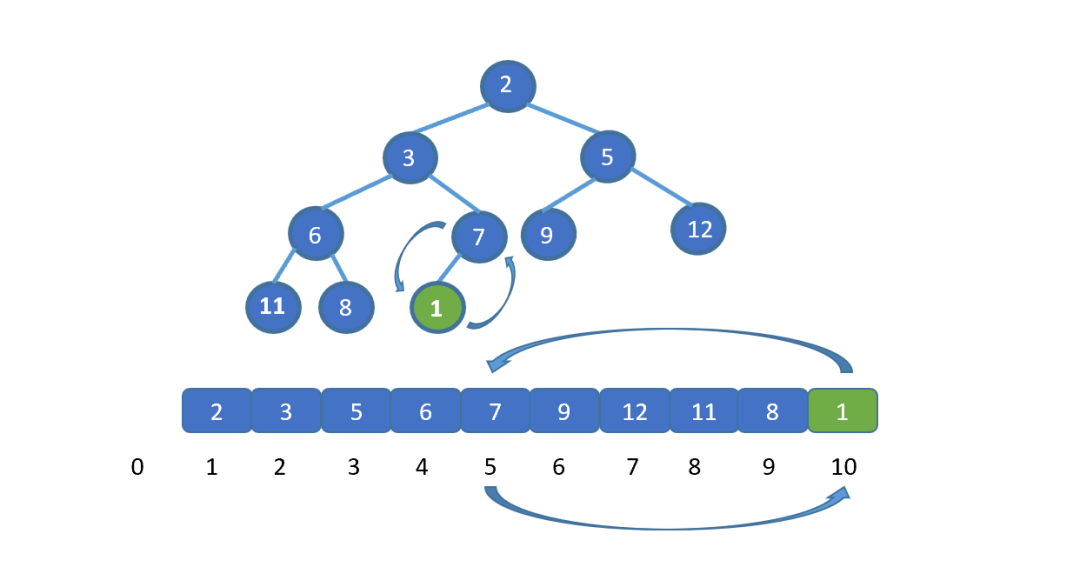 插入元素
插入元素將插入節(jié)點(diǎn)與其父節(jié)點(diǎn),交換。
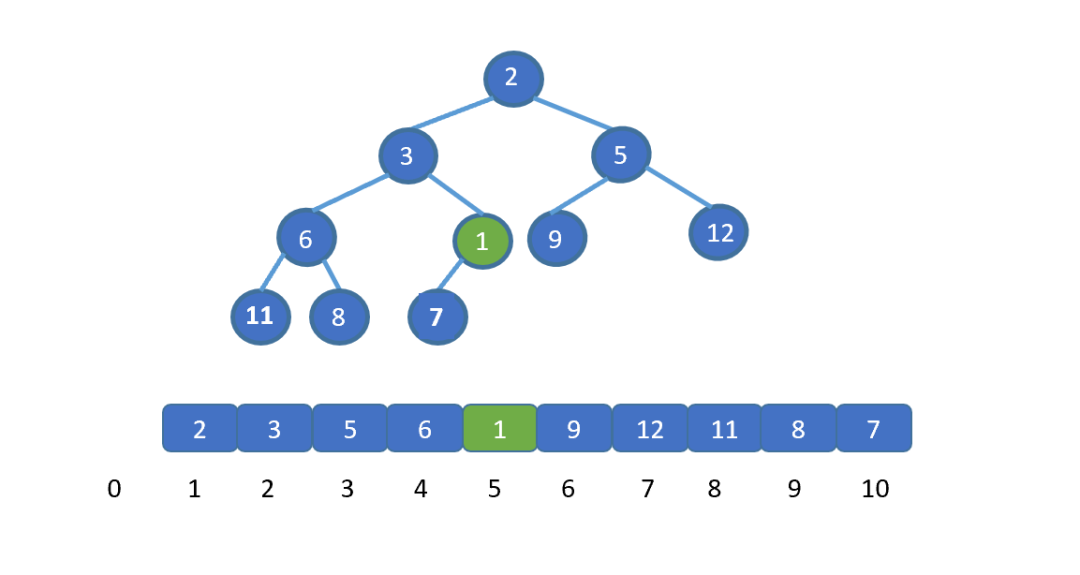 插入元素
插入元素交換之后,我們繼續(xù)將新插入元素,也就是 1 與其父節(jié)點(diǎn)比較,如果大于其父節(jié)點(diǎn),則無(wú)需交換,循環(huán)結(jié)束。
若小于則需要繼續(xù)交換,直到 1 到達(dá)適合他的地方。大家是不是已經(jīng)直到該怎么做啦!下面我們直接看視頻吧。
看完動(dòng)圖是不是就妥了,其實(shí)很簡(jiǎn)單,我們只需將新加入元素與其父節(jié)點(diǎn)比較,判斷是否小于堆頂元素(小頂堆),如果小于則進(jìn)行交換,(讓更小的節(jié)點(diǎn)為父節(jié)點(diǎn))直到符合堆的規(guī)則位置,大頂堆則相反。
我們發(fā)現(xiàn),我們新插入的元素是不是一層層的上浮,直到找到屬于自己的位置,我們將這個(gè)操作稱之為上浮操作。
那我們知道了上浮,豈不是就可以實(shí)現(xiàn)建堆了?
是的,我們則可以依次遍歷數(shù)組,就好比不斷往堆中插入新元素,直至遍歷結(jié)束,這樣我們就完成了建堆,這種方法當(dāng)然是可以的。
我們一起來(lái)看一下上浮操作代碼。
public?void?swim?(int?index)?{
????while?(index?>?1?&&?nums[index/2]?>?nums[index])?{
????????swap(index/2,index);//交換
????????index?=?index/2;
????}
}
既然利用上浮操作建堆已經(jīng)搞懂啦,那么我們?cè)賮?lái)了解一下,利用下沉操作建堆吧,也很容易理解。
利用下沉操作建堆
給我們一個(gè)無(wú)序數(shù)組(不滿足堆的要求),見(jiàn)下圖
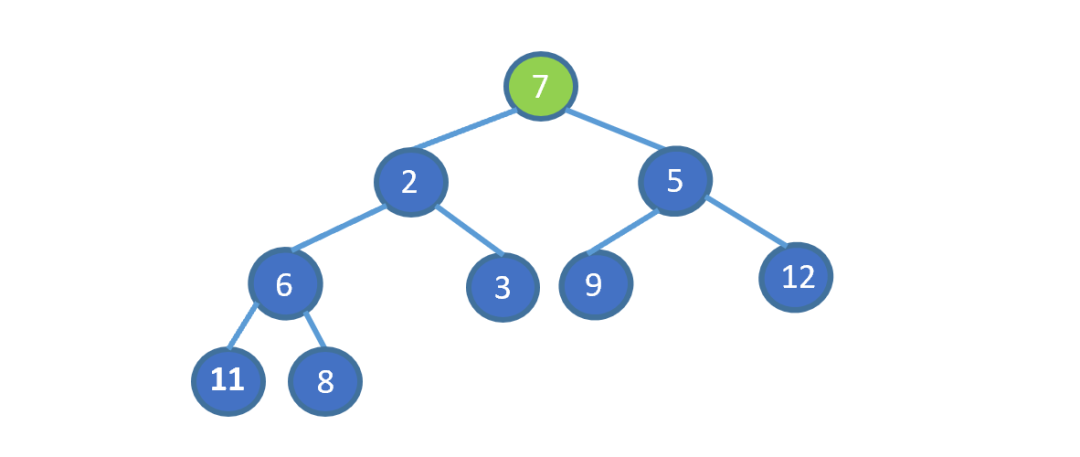
我們發(fā)現(xiàn),7 位于堆頂,但是此時(shí)并不滿足小頂堆的要求,我們需要把 7 放到屬于它的位置,我們應(yīng)該怎么做呢?
廢話不多說(shuō),我們先來(lái)看視頻模擬,看完保準(zhǔn)可以懂
看完視頻是不是懂個(gè)大概了,但是不知道大家有沒(méi)有注意到這個(gè)地方。為什么 7 第一次與其左孩子節(jié)點(diǎn) 2 交換,第二次與右孩子節(jié)點(diǎn) 3 交換。見(jiàn)下圖
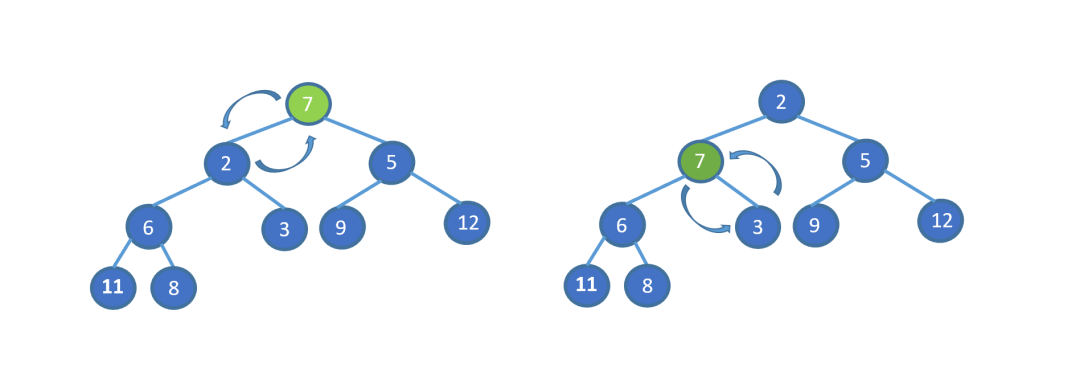
其實(shí)很容易理解,我們需要與孩子節(jié)點(diǎn)中最小的那個(gè)交換,因?yàn)槲覀冃枰粨Q后,父節(jié)點(diǎn)小于兩個(gè)孩子節(jié)點(diǎn),如果我們第一步,7 與 5 進(jìn)行交換的話,則同樣不能滿足小頂堆。
那我們?cè)趺磁袛喙?jié)點(diǎn)找到屬于它的位置了呢?主要有兩個(gè)情況
待下沉元素小于(大于)兩個(gè)子節(jié)點(diǎn),此時(shí)符合堆的規(guī)則,無(wú)序下沉,例如上圖中的 6
下沉為葉子節(jié)點(diǎn),此時(shí)沒(méi)有子節(jié)點(diǎn),例如 7 下沉到最后變成了葉子節(jié)點(diǎn)。
我們將上面的操作稱之為下沉操作。
這時(shí)我們又有疑問(wèn)了,下沉操作我懂了,但是這跟建堆有個(gè)錘子關(guān)系啊!
不要急,我們繼續(xù)來(lái)看視頻,這次我們通過(guò)下沉操作建個(gè)大頂堆。
初始數(shù)組 [8,5,7,9,2,10,1,4,6,3]
我們一起來(lái)拆解一下視頻,我們只需要從最后一個(gè)非葉子節(jié)點(diǎn)開(kāi)始,依次執(zhí)行下沉操作。執(zhí)行完畢后我們就能夠完成堆化。是不是一下就懂了呀。
好啦我們一起看哈下沉操作的代碼(代碼沒(méi)有簡(jiǎn)寫(xiě),可以結(jié)合動(dòng)畫(huà)一起理解)。
public?void?sink?(int[]?nums,?int?index,int?len)?{
??????while?(true)?{
??????????//獲取子節(jié)點(diǎn)
??????????int?j?=?2?*?index;
??????????if?(j?<?len-1?&&?nums[j]?<?nums[j+1])?{
??????????????j++;
??????????}
???????????//交換操作,父節(jié)點(diǎn)下沉,與最大的孩子節(jié)點(diǎn)交換
??????????if?(j?<?len?&&?nums[index]?<?nums[j])?{
??????????????swap(nums,index,j);
??????????}?else?{
??????????????break;
??????????}?
???????????//繼續(xù)下沉
??????????index?=?j;
????????}
????}
好啦,兩種建堆方式我們都已經(jīng)了解啦,那么我們如何進(jìn)行排序呢?
了解排序之前我們先來(lái),看一下如何刪除堆頂元素,我們需要保證的是,刪除堆頂元素后,其他元素仍能滿足堆的要求,我們思考一下如何實(shí)現(xiàn)呢?見(jiàn)下圖
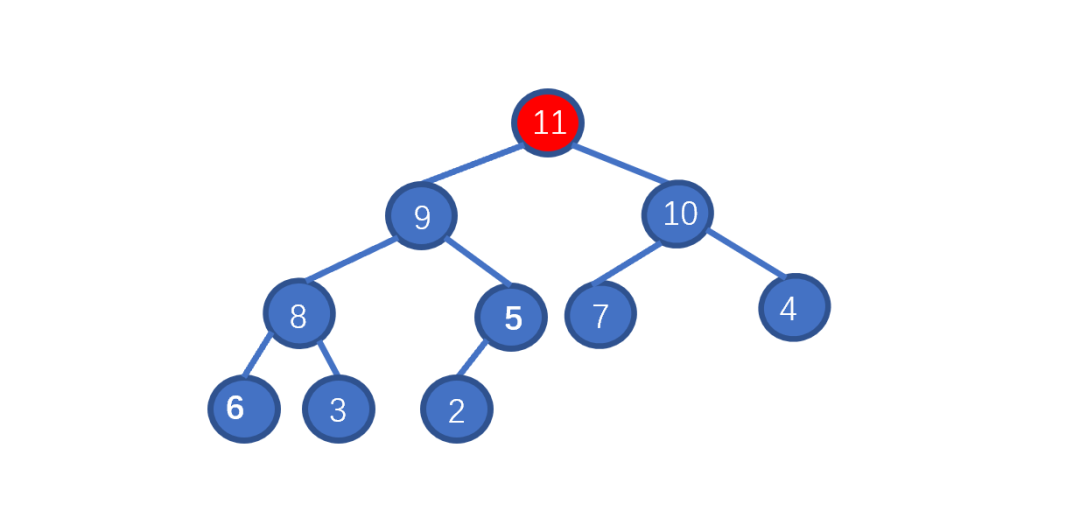
假設(shè)我們想要去除堆頂?shù)?11 ,那我們則需要將其與堆的最后一個(gè)節(jié)點(diǎn)交換也就是 2 ,2然后再執(zhí)行下沉操作,執(zhí)行完畢后仍能滿足堆的要求,見(jiàn)下圖
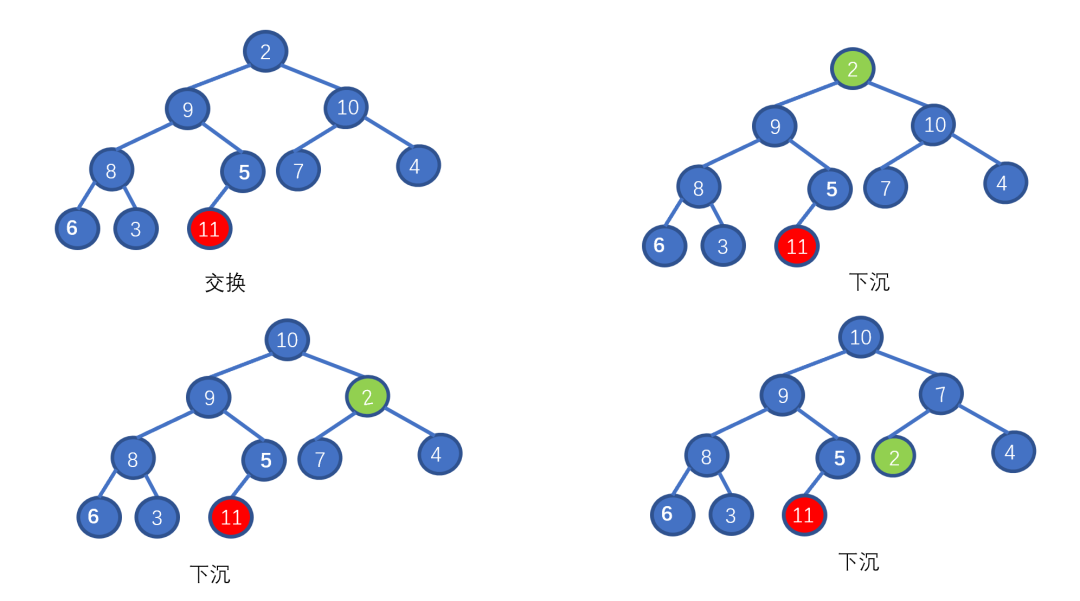
好啦,其實(shí)你已經(jīng)學(xué)會(huì)如何排序啦!你不信?那我給你放視頻
好啦,大家是不是已經(jīng)搞懂啦,就是先將堆頂元素與堆的最后一個(gè)元素進(jìn)行交換,然后將新的堆頂元素執(zhí)行下沉操作。重復(fù)執(zhí)行上訴步驟直至完全有序。
下面我們總結(jié)一下堆排序的具體執(zhí)行過(guò)程
1.建堆,通過(guò)下沉操作建堆效率更高,具體過(guò)程是,找到最后一個(gè)非葉子節(jié)點(diǎn),然后從后往前遍歷執(zhí)行下沉操作。
2.排序,將堆頂元素(代表最大元素)與最后一個(gè)元素交換,然后新的堆頂元素進(jìn)行下沉操作,遍歷執(zhí)行上訴操作,則可以完成排序。
好啦,下面我們一起看代碼吧
class?Solution?{
????public?int[]?sortArray(int[]?nums)?{
????????int?len?=?nums.length;
????????int[]?a?=?new?int[len?+?1];
????????for?(int?i?=?0;?i?<?nums.length;?++i)?{
????????????a[i+1]?=?nums[i];
????????}??????????
????????//下沉建堆
????????for?(int?i?=?len/2;?i?>=?1;?--i)?{
????????????sink(a,i,len);
????????}
????????int?k?=?len;
????????//排序
????????while?(k?>?1)?{
????????????swap(a,1,k--);
????????????sink(a,1,k);
????????}
????????for?(int?i?=?1;?i?<?len+1;?++i)?{
????????????nums[i-1]?=?a[i];
????????}
????????return?nums;
????}
????public?void?sink?(int[]?nums,?int?k,int?end)?{
????????//下沉
????????while?(2?*?k?<=?end)?{
????????????int?j?=?2?*?k;
????????????//找出子節(jié)點(diǎn)中最大或最小的那個(gè)
????????????if?(j?+?1?<=?end?&&?nums[j?+?1]?>?nums[j])?{
????????????????j++;
????????????}
????????????if?(nums[j]?>?nums[k])?{
????????????????swap(nums,?j,?k);
????????????}?else?{
????????????????break;
????????????}
????????????k?=?j;
????????}
????}
????public?void?swap?(int?nums[],?int?i,?int?j)?{
????????int?temp?=?nums[i];
????????nums[i]?=?nums[j];
????????nums[j]?=?temp;
????}
}
好啦,堆排序我們就到這里啦,是不是搞定啦,總的來(lái)說(shuō)堆排序比其他排序算法稍微難理解一些,重點(diǎn)就是建堆,而且應(yīng)用比較廣泛,大家記得打卡呀。
好啦,我們?cè)賮?lái)分析一下堆排序的時(shí)間復(fù)雜度、空間復(fù)雜度以及穩(wěn)定性。
堆排序時(shí)間復(fù)雜度分析
因?yàn)槲覀兘ǘ训臅r(shí)間復(fù)雜度為 O(n),排序過(guò)程的時(shí)間復(fù)雜度為 O(nlogn),所以總的時(shí)間復(fù)雜度為 O(nlogn)
堆排序空間復(fù)雜度分析
這里需要注意,我們上面的描述過(guò)程中,為了更直觀的描述,空出數(shù)組的第一位,這樣我們就可以通過(guò) i * 2 和 i * 2+1 來(lái)求得左孩子節(jié)點(diǎn)和右孩子節(jié)點(diǎn) 。
我們也可以根據(jù) ?i * 2 + 1 和 i * 2 + 2 ?來(lái)獲取孩子節(jié)點(diǎn),這樣則不需要臨時(shí)數(shù)組來(lái)處理原數(shù)組,將所有元素后移一位,所以堆排序的空間復(fù)雜度為 O(1),是原地排序算法。
堆排序穩(wěn)定性分析
堆排序不是穩(wěn)定的排序算法,在排序的過(guò)程,我們會(huì)將堆的最后一個(gè)節(jié)點(diǎn)跟堆頂節(jié)點(diǎn)交換,改變相同元素的原始相對(duì)位置。
最后我們來(lái)比較一下我們快速排序和堆排序
1.對(duì)于快速排序來(lái)說(shuō),數(shù)據(jù)是順序訪問(wèn)的。而對(duì)于堆排序來(lái)說(shuō),數(shù)據(jù)是跳著訪問(wèn)的。這樣對(duì) CPU 緩存是不友好的
2.相同的的數(shù)據(jù),排序過(guò)程中,堆排序的數(shù)據(jù)交換次數(shù)要多于快速排序。
所以上面兩條也就說(shuō)明了在實(shí)際開(kāi)發(fā)中,堆排序的性能不如快速排序性能好。
好啦,今天的內(nèi)容就到這里啦,咱們下期見(jiàn)。
巨人的肩膀
《算法》,《數(shù)據(jù)結(jié)構(gòu)與算法之美》小爭(zhēng)哥
