得嘞,一文把前綴和給扒的干干凈凈。

今天我們來(lái)說(shuō)一下刷題時(shí)經(jīng)常用到的前綴和思想，前綴和和滑動(dòng)窗口會(huì)經(jīng)常用在求子數(shù)組和子串問(wèn)題上，當(dāng)我們遇到此類問(wèn)題時(shí)，則應(yīng)該首先想到此類解題方式，該文章會(huì)深入淺出描述前綴和，讀完這個(gè)文章就會(huì)有屬于自己的解題框架，遇到此類問(wèn)題時(shí)就能夠輕松應(yīng)對(duì)，我個(gè)人建議做題時(shí)不要背代碼模板，應(yīng)該自己進(jìn)行總結(jié)，下次遇到時(shí)自然而然就能寫出了。

下面我們先來(lái)了解一下什么是前綴和。

前綴和其實(shí)我們很早之前就了解過(guò)的，我們求數(shù)列的和時(shí)，Sn = a1+a2+a3+...an; 此時(shí)Sn就是數(shù)列的前 n 項(xiàng)和。例 S5 = a1 + a2 + ?a3 + a4 + a5; S2 = a1 + a2。所以我們完全可以通過(guò) S5-S2 得到 a3+a4+a5 的值，這個(gè)過(guò)程就和我們做題用到的前綴和思想類似。我們的前綴和數(shù)組里保存的就是前 n 項(xiàng)的和。見下圖

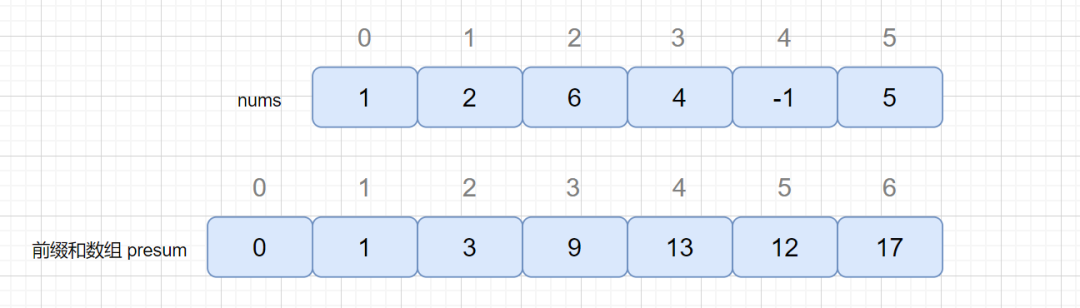
我們通過(guò)前綴和數(shù)組保存前 n 位的和，presum[1]保存的就是 nums 數(shù)組中前 1 位的和，也就是 presum[1] = nums[0], presum[2] = nums[0] + nums[1] = presum[1] + nums[1]. 依次類推，所以我們通過(guò)前綴和數(shù)組可以輕松得到每個(gè)區(qū)間的和。

例如我們需要獲取 ?nums[2] ?到 ?nums[4] ?這個(gè)區(qū)間的和，我們則可以完全根據(jù) presum 數(shù)組得到，是不是有點(diǎn)和我們之前說(shuō)的字符串匹配算法中 BM,KMP 中的 next 數(shù)組和 suffix 數(shù)組作用類似。那么我們?cè)趺锤鶕?jù) presum 數(shù)組獲取 nums[2] 到 nums[4] 區(qū)間的和呢？見下圖

好啦，我們已經(jīng)了解了前綴和的解題思想了，我們可以通過(guò)下面這段代碼得到我們的前綴和數(shù)組，非常簡(jiǎn)單

好啦，我們開始實(shí)戰(zhàn)吧。

? ?leetcode 724. 尋找數(shù)組的中心索引

題目描述

給定一個(gè)整數(shù)類型的數(shù)組 nums，請(qǐng)編寫一個(gè)能夠返回?cái)?shù)組 “中心索引” 的方法。

我們是這樣定義數(shù)組 中心索引 的：數(shù)組中心索引的左側(cè)所有元素相加的和等于右側(cè)所有元素相加的和。

如果數(shù)組不存在中心索引，那么我們應(yīng)該返回 -1。如果數(shù)組有多個(gè)中心索引，那么我們應(yīng)該返回最靠近左邊的那一個(gè)。

示例 1：

輸入：nums = [1, 7, 3, 6, 5, 6] 輸出：3

解釋：索引 3 (nums[3] = 6) 的左側(cè)數(shù)之和 (1 + 7 + 3 = 11)，與右側(cè)數(shù)之和 (5 + 6 = 11) 相等。同時(shí), 3 也是第一個(gè)符合要求的中心索引。

示例 2：

輸入：nums = [1, 2, 3] 輸出：-1

解釋：數(shù)組中不存在滿足此條件的中心索引。

解析

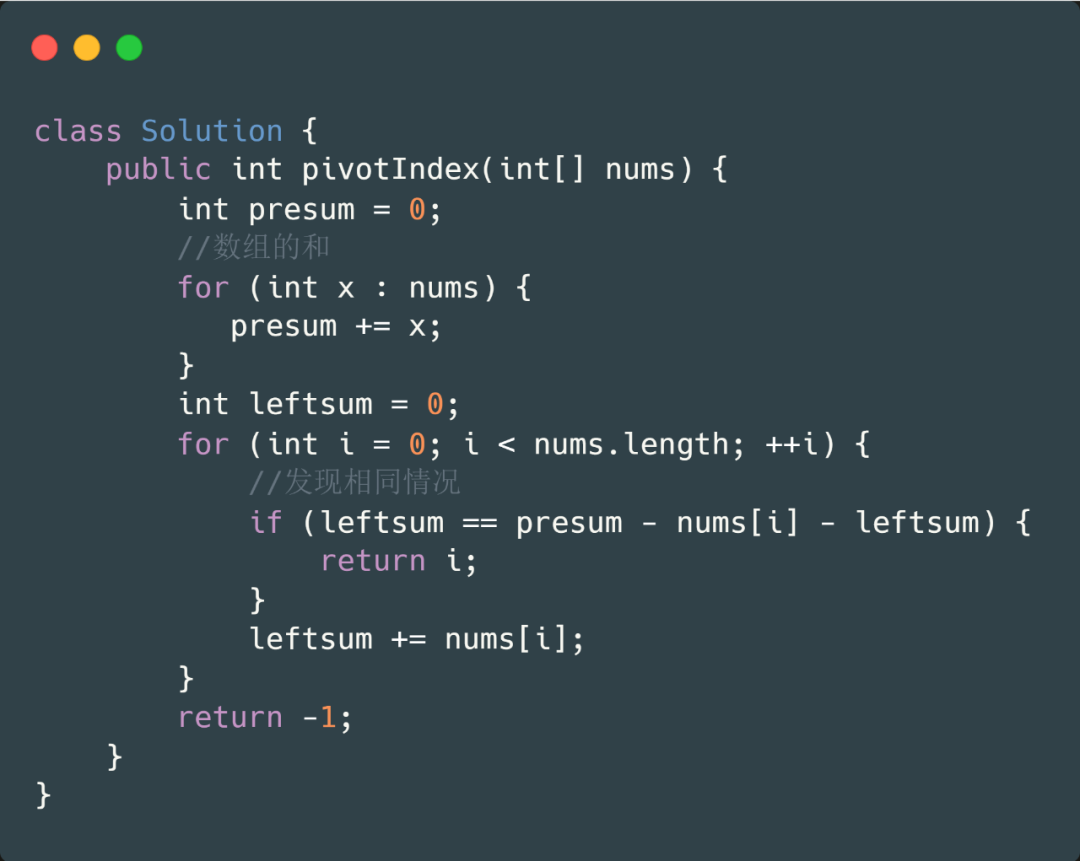
理解了我們前綴和的概念（不了解好像也可以做，這個(gè)題太簡(jiǎn)單了哈哈）。我們可以一下就能把這個(gè)題目做出來(lái)，先遍歷一遍求出數(shù)組的和，然后第二次遍歷時(shí)，直接進(jìn)行對(duì)比左半部分和右半部分是否相同，如果相同則返回 true，不同則繼續(xù)遍歷。

? ?leetcode 560. 和為K的子數(shù)組

題目描述

給定一個(gè)整數(shù)數(shù)組和一個(gè)整數(shù) k，你需要找到該數(shù)組中和為 k 的連續(xù)的子數(shù)組的個(gè)數(shù)。

示例 1 :

輸入:nums = [1,1,1], k = 2 輸出: 2 , [1,1] 與 [1,1] 為兩種不同的情況。

暴力法

解析

我們先來(lái)用暴力法解決這個(gè)題目，很簡(jiǎn)單，一下就能 AC。

這個(gè)題目的題意很容易理解，就是讓我們返回和為 k 的子數(shù)組的個(gè)數(shù)，所以我們直接利用雙重循環(huán)解決該題，這個(gè)是很容易想到的。我們直接看代碼吧。

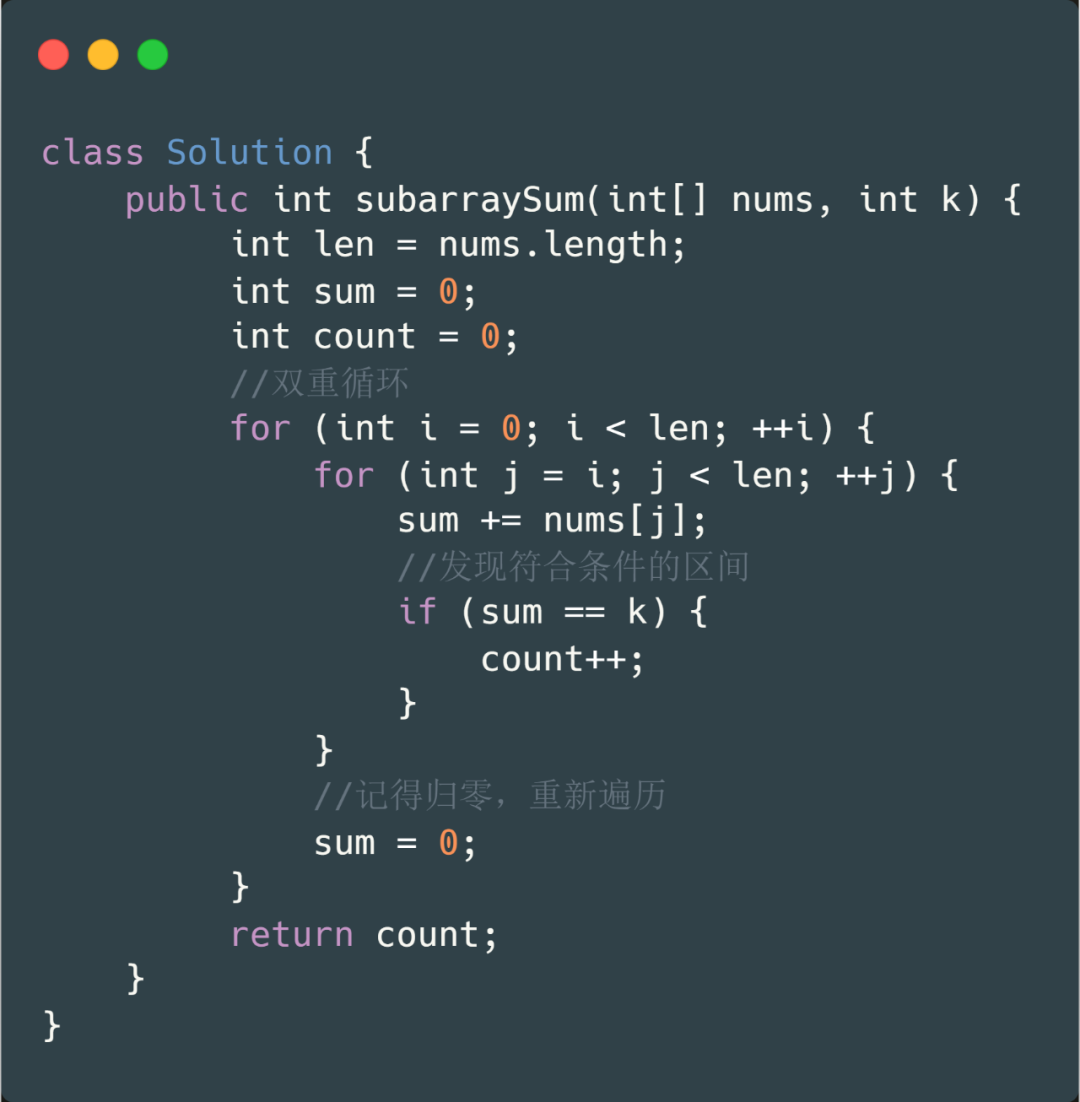
好啦，既然我們已經(jīng)知道如何求前綴和數(shù)組，那我們來(lái)看一下如何用前綴和數(shù)組來(lái)解決這個(gè)問(wèn)題。

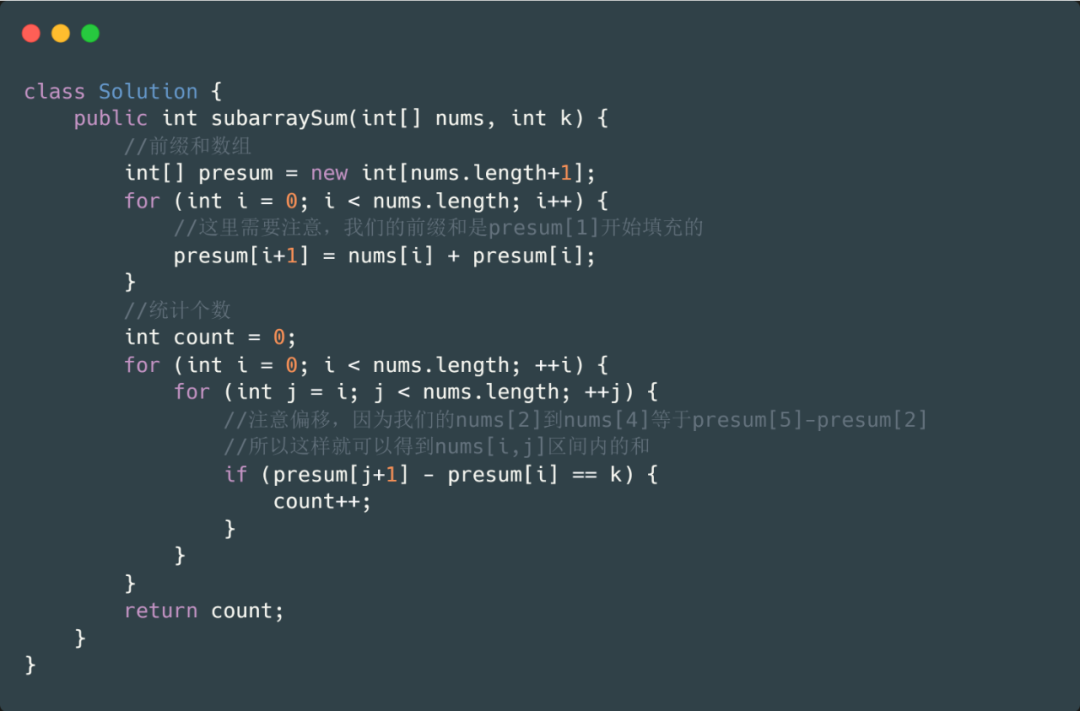
我們分析上面的代碼，發(fā)現(xiàn)該代碼雖然用到了前綴和數(shù)組，但是對(duì)比暴力法并沒(méi)有提升性能，時(shí)間復(fù)雜度仍為O(n^2)，空間復(fù)雜度卻成了 O(n)。那我們有沒(méi)有其他方法解決呢？

前綴和 + HashMap

了解這個(gè)方法前，我們先來(lái)看一下下面這段代碼，保證你很熟悉

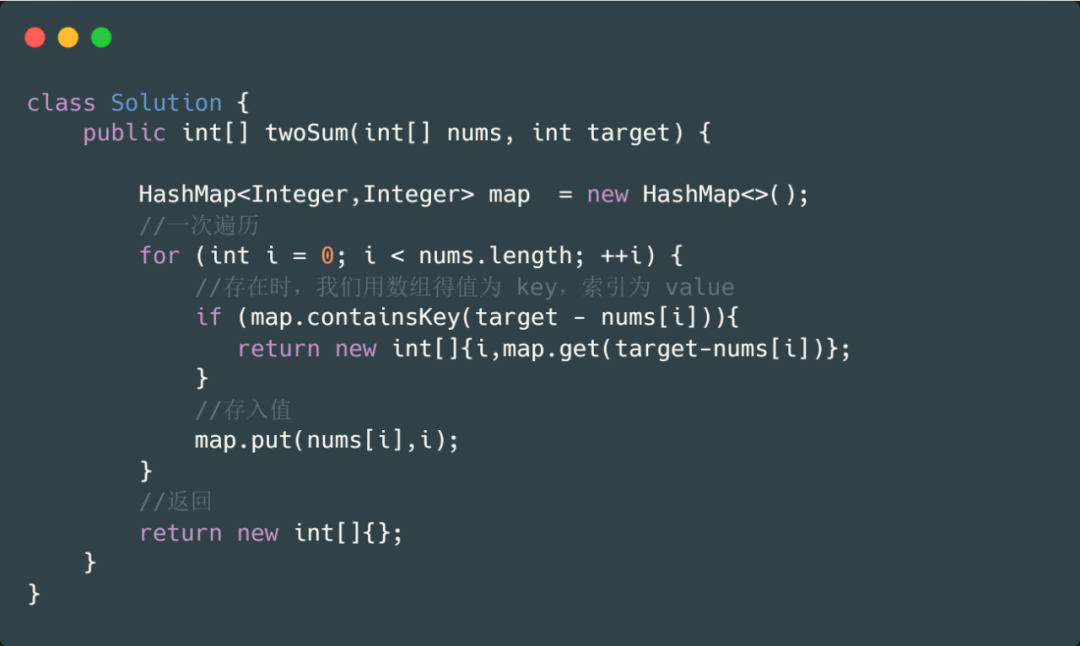
上面的這段代碼是不是賊熟悉，沒(méi)錯(cuò)就是那個(gè)快被我們做爛的兩數(shù)之和。這一段代碼就是用到了我們的前綴和+ HashMap 思想，那么我們?nèi)绾瓮ㄟ^(guò)這個(gè)方法來(lái)解決這個(gè)題目呢？

在上面的代碼中，我們將數(shù)組的值和索引存入 map 中，當(dāng)我們遍歷到某一值 x 時(shí)，判斷 map 中是否含有 target - x，即可。

其實(shí)我們現(xiàn)在這個(gè)題目和兩數(shù)之和原理是一致的，只不過(guò)我們是將所有的前綴和該前綴和出現(xiàn)的次數(shù)存到了 map 里。下面我們來(lái)看一下代碼的執(zhí)行過(guò)程。

我們來(lái)拆解一下動(dòng)圖，可能有的同學(xué)會(huì)思考為什么我們只要查看是否含有 ?presum - k ，并獲取到presum - k 出現(xiàn)的次數(shù)就行呢？見下圖

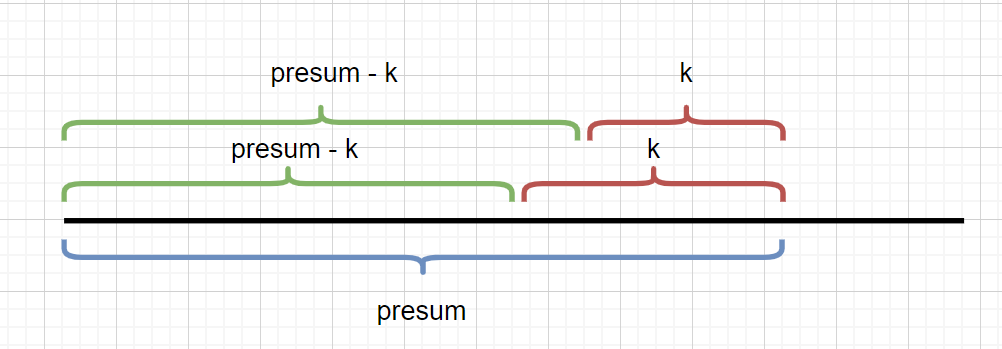
因?yàn)槲覀兇藭r(shí) presum 已知，如果知道了presum - k 的個(gè)數(shù)，也就知道了 k 的個(gè)數(shù)。所以我們完全可以通過(guò) presum - k的個(gè)數(shù)獲得 k 的個(gè)數(shù)

好啦我們來(lái)看一下代碼吧

做完這個(gè)題目，各位也可以去完成一下這個(gè)題目，兩個(gè)題目幾乎完全相同 leetcode 930. 和相同的二元子數(shù)組

? ?leetcode1248. 統(tǒng)計(jì)「優(yōu)美子數(shù)組」

題目描述

給你一個(gè)整數(shù)數(shù)組 nums 和一個(gè)整數(shù) k。

如果某個(gè) 連續(xù) 子數(shù)組中恰好有 k 個(gè)奇數(shù)數(shù)字，我們就認(rèn)為這個(gè)子數(shù)組是「優(yōu)美子數(shù)組」。

請(qǐng)返回這個(gè)數(shù)組中「優(yōu)美子數(shù)組」的數(shù)目。

示例 1：

輸入：nums = [1,1,2,1,1], k = 3 輸出：2 解釋：包含 3 個(gè)奇數(shù)的子數(shù)組是 [1,1,2,1] 和 [1,2,1,1] 。

示例 2：

輸入：nums = [2,4,6], k = 1 輸出：0 解釋：數(shù)列中不包含任何奇數(shù)，所以不存在優(yōu)美子數(shù)組。

示例 3：

輸入：nums = [2,2,2,1,2,2,1,2,2,2], k = 2 輸出：16

如果上面那個(gè)題目我們完成了，這個(gè)題目做起來(lái)，分分鐘的事，不信你去寫一哈，百分百就整出來(lái)了，我們繼續(xù)按上面的思想來(lái)解決。

前綴和 + HashMap

解析

上個(gè)題目我們是求和為 K 的子數(shù)組，這個(gè)題目是讓我們求 恰好有 ?k 個(gè)奇數(shù)數(shù)字的連續(xù)子數(shù)組，這兩個(gè)題幾乎是一樣的，上個(gè)題中我們將前綴區(qū)間的和保存到哈希表中，這個(gè)題目我們只需將前綴區(qū)間的奇數(shù)個(gè)數(shù)保存到區(qū)間內(nèi)即可，只不過(guò)將 sum += x 改成了判斷奇偶的語(yǔ)句，見下圖。

我們來(lái)解析一下哈希表，key 代表的是含有 1 個(gè)奇數(shù)的前綴區(qū)間，value 代表這種子區(qū)間的個(gè)數(shù)，含有兩個(gè)，也就是nums[0],nums[0,1].后面含義相同，那我們下面直接看代碼吧，一下就能讀懂。

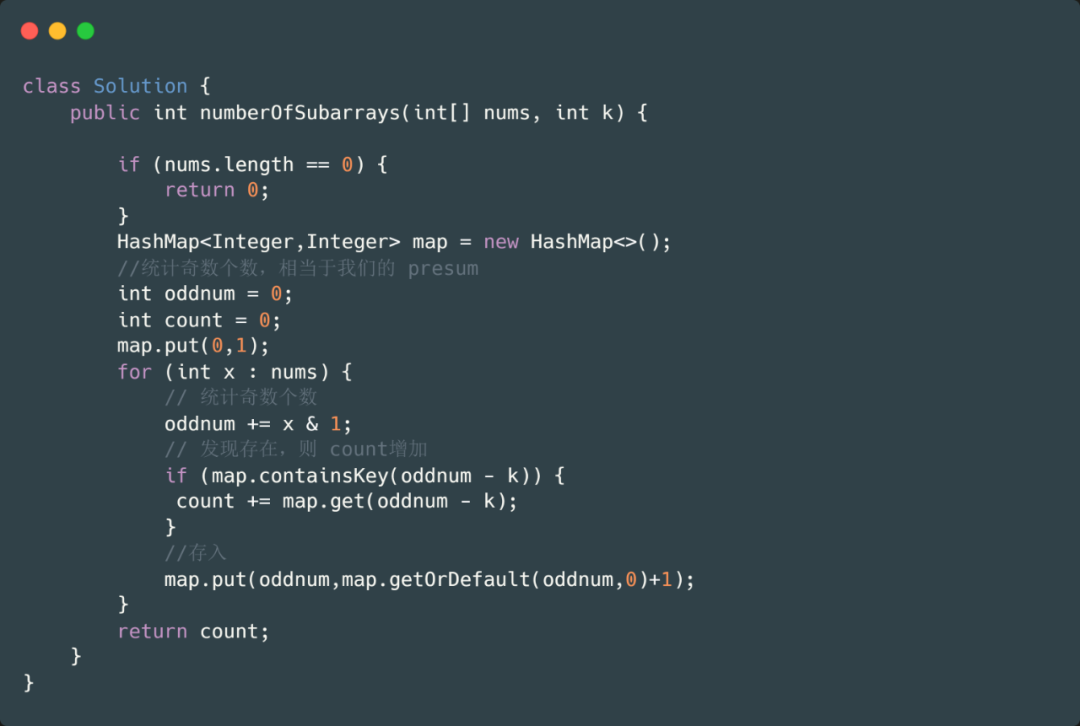
但是也有一點(diǎn)不同，就是我們是統(tǒng)計(jì)奇數(shù)的個(gè)數(shù)，數(shù)組中的奇數(shù)個(gè)數(shù)肯定不會(huì)超過(guò)原數(shù)組的長(zhǎng)度，所以這個(gè)題目中我們可以用數(shù)組來(lái)模擬 HashMap ，用數(shù)組的索引來(lái)模擬 HashMap 的 key，用值來(lái)模擬哈希表的 value。下面我們直接看代碼吧。

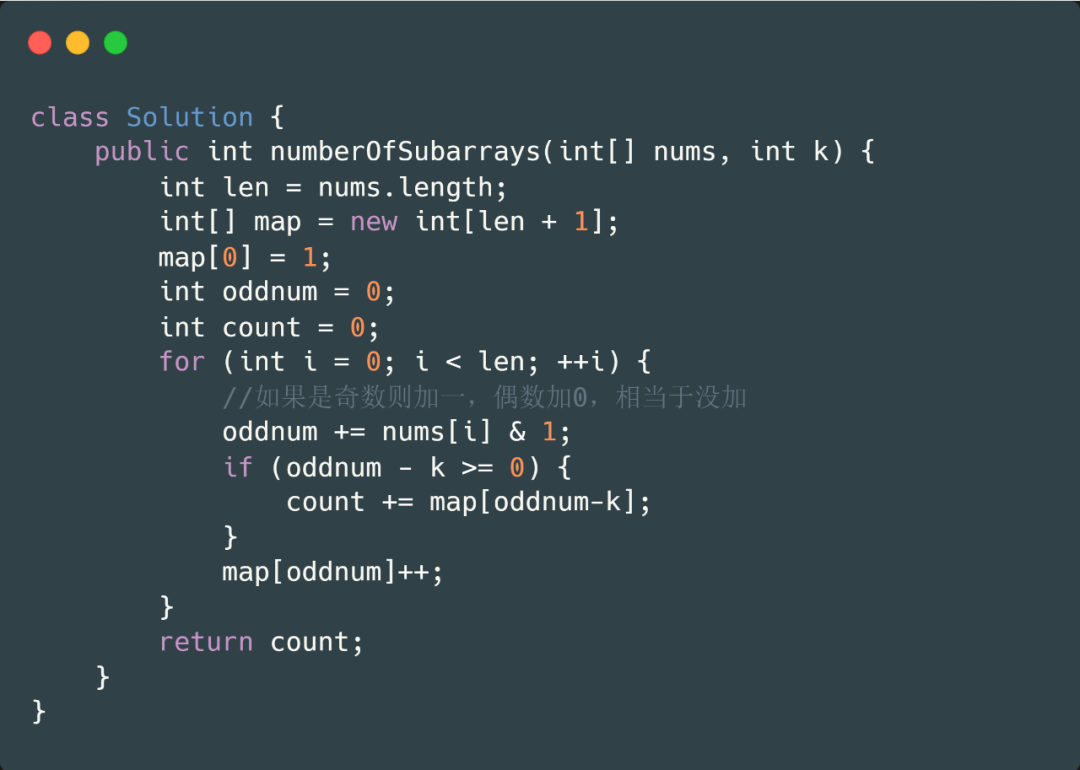
leetcode 974 和可被 K 整除的子數(shù)組

題目描述

給定一個(gè)整數(shù)數(shù)組 A，返回其中元素之和可被 K 整除的（連續(xù)、非空）子數(shù)組的數(shù)目。

示例：

輸入：A = [4,5,0,-2,-3,1], K = 5 輸出：7

解釋：

有 7 個(gè)子數(shù)組滿足其元素之和可被 K = 5 整除：[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

前綴和+HashMap

解析

我們?cè)谠撐牡牡诙} 和為K的子數(shù)組 中，我們需要求出滿足條件的區(qū)間，見下圖

我們需要找到滿足，和為 K 的區(qū)間。我們此時(shí) presum 是已知的，k 也是已知的，我們只需要找到 presum - k 區(qū)間的個(gè)數(shù)，就能得到 k 的區(qū)間個(gè)數(shù)。但是我們?cè)诋?dāng)前題目中應(yīng)該怎么做呢？見下圖。

我們?cè)谥暗睦又姓f(shuō)到，presum[j+1] - presum[i] ?可以得到 nums[i] + nums[i+1]+.... nums[j]，也就是[i,j]區(qū)間的和。

那么我們想要判斷區(qū)間 [i,j] 的和是否能整除 K，也就是上圖中紅色那一段是否能整除 K，那么我們只需判斷

(presum[j+1] - presum[i] ) % k 是否等于 0 即可，

我們假設(shè) (presum[j+1] - presum[i] ) % k ?== 0；則

presum[j+1] % k ?- ?presum[i] % k == 0;

presum[j +1] % k = presum[i] % k ;

我們 presum[j +1] % k 的值 key 是已知的，即是當(dāng)前的 presum 和 k 的關(guān)系，所以我們只需要知道 presum[i] 和 presum[j+1] % k 含有相同余數(shù)時(shí)，i 有幾種情況。這樣就能夠知道當(dāng)前能夠整除 K 的區(qū)間個(gè)數(shù)。見下圖

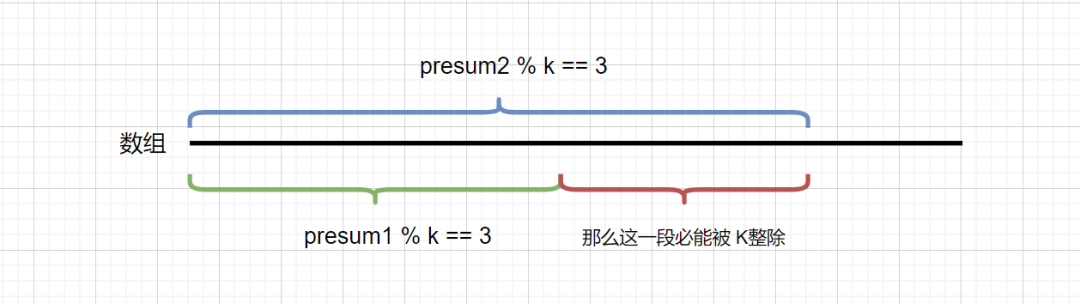
題目代碼

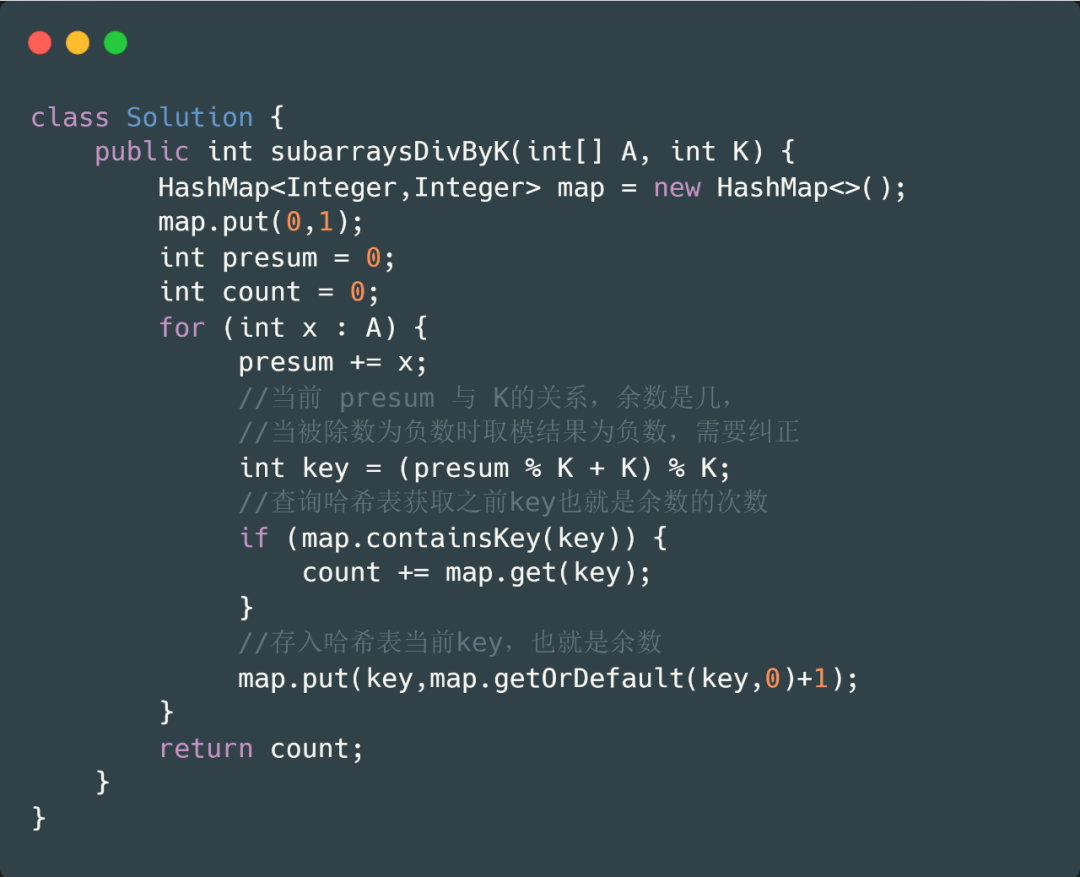
我們看到上面代碼中有一段代碼是這樣的

這是為什么呢？不能直接用 presum % k 嗎？

這是因?yàn)楫?dāng)我們 presum 為負(fù)數(shù)時(shí)，需要對(duì)其糾正。糾正前(-1) %2 = (-1)，糾正之后 ( (-1) % 2 + 2) % 2=1 保存在哈希表中的則為 1.則不會(huì)漏掉部分情況.

例如輸入為 [-1,2,9],K = 2如果不對(duì)其糾正則會(huì)漏掉區(qū)間 [2] 此時(shí) 2 % 2 = 0，符合條件，但是不會(huì)被計(jì)數(shù)。

那么這個(gè)題目我們可不可以用數(shù)組，代替 map 呢？當(dāng)然也是可以的，因?yàn)榇藭r(shí)我們的哈希表存的是余數(shù)，余數(shù)最大也只不過(guò)是 K-1所以我們可以用固定長(zhǎng)度 K 的數(shù)組來(lái)模擬哈希表。

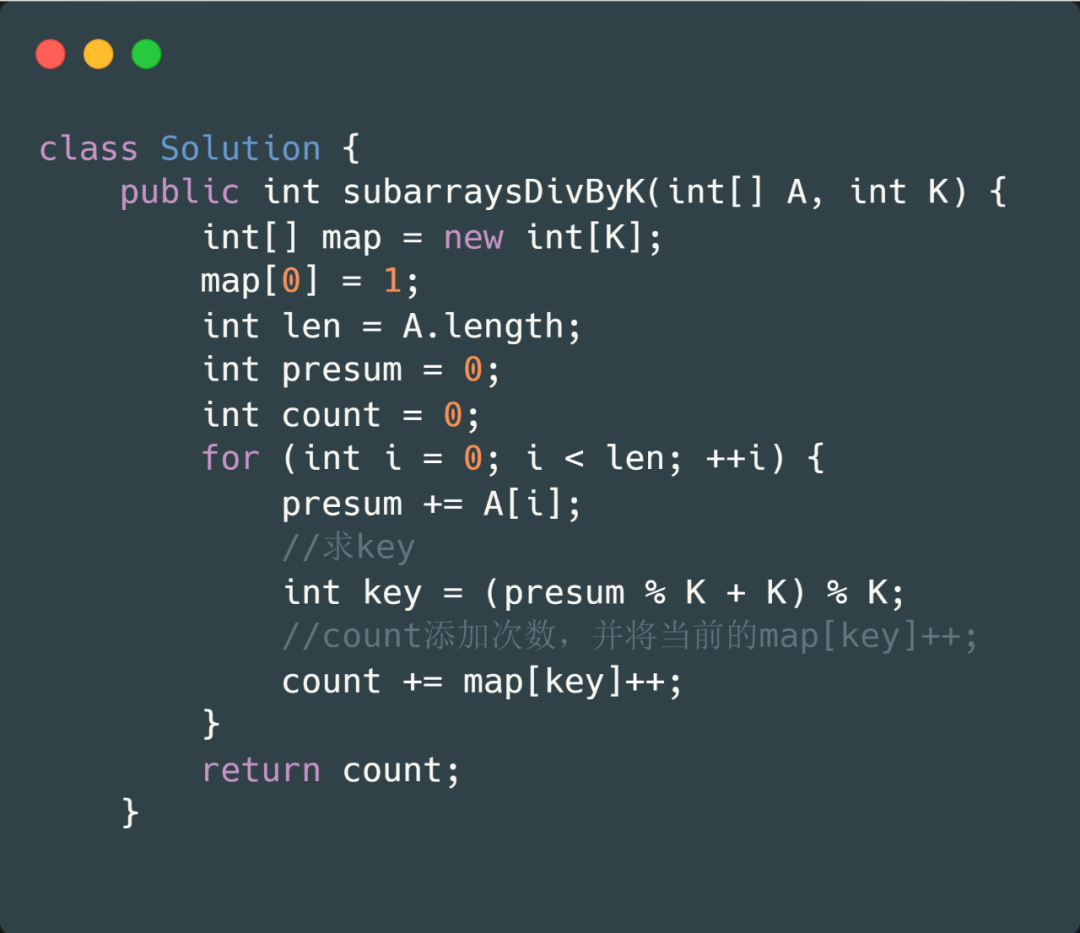
? ?leetcode 523 連續(xù)的子數(shù)組和

題目描述

給定一個(gè)包含 非負(fù)數(shù) 的數(shù)組和一個(gè)目標(biāo) 整數(shù) k，編寫一個(gè)函數(shù)來(lái)判斷該數(shù)組是否含有連續(xù)的子數(shù)組，其大小至少為 2，且總和為 k 的倍數(shù)，即總和為 n*k，其中 n 也是一個(gè)整數(shù)。

示例 1：

輸入：[23,2,4,6,7], k = 6 輸出：True

解釋：[2,4] 是一個(gè)大小為 2 的子數(shù)組，并且和為 6。

示例 2：

輸入：[23,2,6,4,7], k = 6 輸出：True

解釋：[23,2,6,4,7]是大小為 5 的子數(shù)組，并且和為 42。

前綴和 + HashMap

這個(gè)題目算是對(duì)剛才那個(gè)題目的升級(jí)，前半部分是一樣的，都是為了讓你找到能被 K 整除的子數(shù)組，但是這里加了一個(gè)限制，那就是子數(shù)組的大小至少為 2，那么我們應(yīng)該怎么判斷子數(shù)組的長(zhǎng)度呢？我們可以根據(jù)索引來(lái)進(jìn)行判斷，見下圖。

此時(shí)我們 K = 6, presum % 6 = 4 ?也找到了相同余數(shù)的前綴子數(shù)組 [0,1] 但是我們此時(shí)指針指向?yàn)?2，我們的前綴子區(qū)間 [0,1]的下界為1，所以 2 - 1 = 1，但我們的中間區(qū)間的長(zhǎng)度小于2，所以不能返回 true，需要繼續(xù)遍歷.

那我們有兩個(gè)區(qū)間[0,1],[0,2]都滿足 presum % 6 = 4，那我們哈希表中保存的下標(biāo)應(yīng)該是 1 還是 2 呢？我們保存的是1，如果我們保存的是較大的那個(gè)索引，則會(huì)出現(xiàn)下列情況，見下圖。

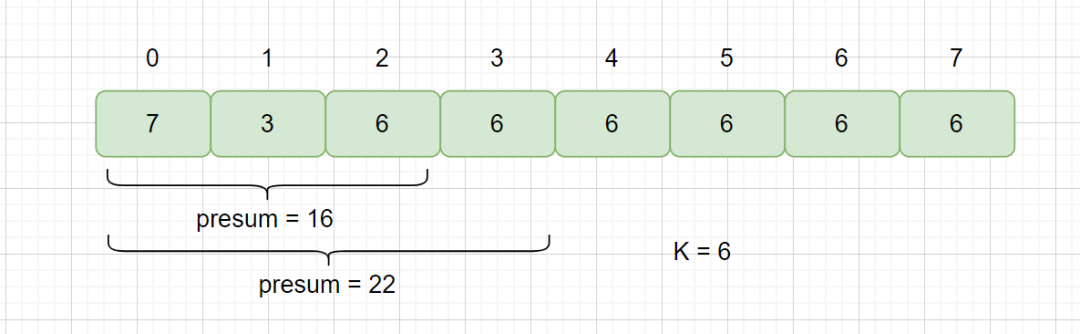
此時(shí)，仍會(huì)顯示不滿足子區(qū)間長(zhǎng)度至少為 2 的情況，仍會(huì)繼續(xù)遍歷，但是我們此時(shí)的? [2,3] 區(qū)間已經(jīng)滿足該情況，應(yīng)該返回 true，所以我們往哈希表存值時(shí)，只存一次，即最小的索引即可。下面我們看一下該題的兩個(gè)細(xì)節(jié)

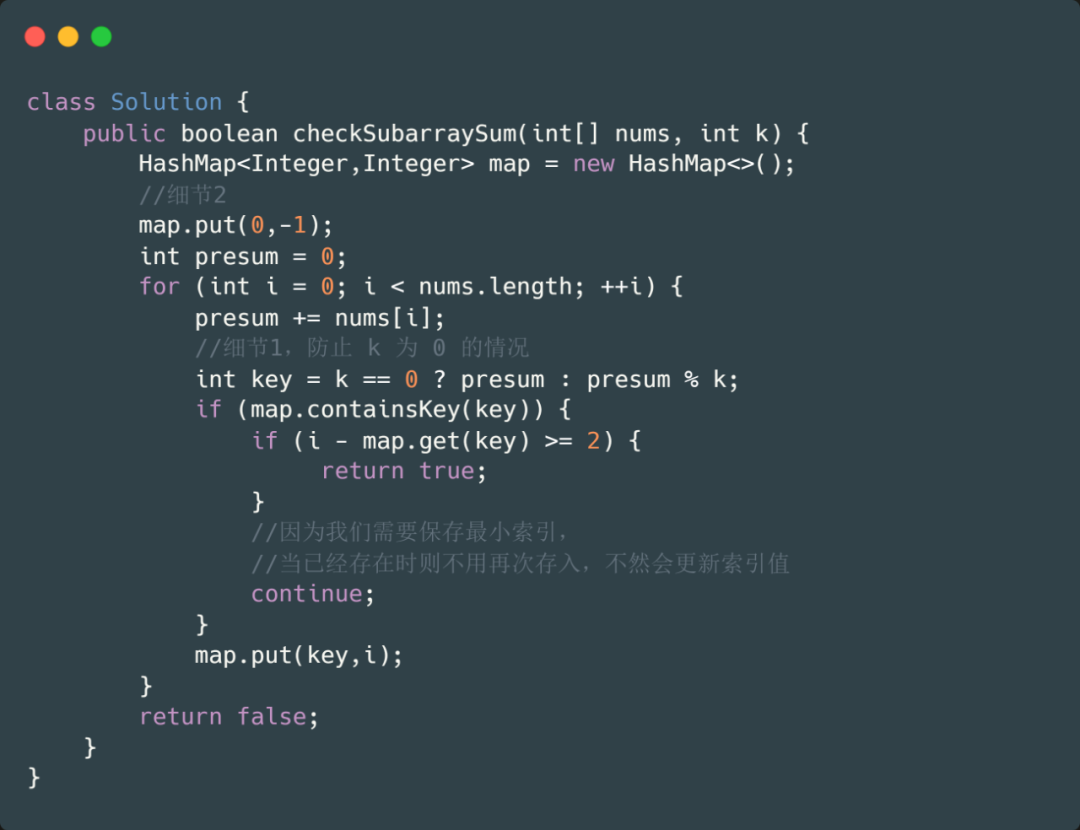
細(xì)節(jié)1：我們的 k 如果為 0 時(shí)怎么辦，因?yàn)?0 不可以做除數(shù)。所以當(dāng)我們 k 為 0 時(shí)可以直接存到數(shù)組里，例如輸入為 ?[0,0] , K = 0 的情況

細(xì)節(jié)2：另外一個(gè)就是之前我們都是統(tǒng)計(jì)個(gè)數(shù)，value 里保存的是次數(shù)，但是此時(shí)我們加了一個(gè)條件就是長(zhǎng)度至少為 2，保存的是索引，所以我們不能繼續(xù) map.put(0,1)，應(yīng)該賦初值為 map.put(0,-1)。這樣才不會(huì)漏掉一些情況，例如我們的數(shù)組為[2,3,4],k = 1,當(dāng)我們 map.put(0,-1) 時(shí)，當(dāng)我們遍歷到 nums[1] 即 3 時(shí)，則可以返回 true，因?yàn)?1-（-1）= 2，5 % 1=0 , 同時(shí)滿足。

視頻解析

下面我們直接看代碼吧，一下就能?整懂啦。

--end--