本文我們將說明如何量化選擇最佳模型過程中涉及的隨機性。
kaggle比賽里經(jīng)常會發(fā)生shake up的現(xiàn)象,說的直接點就是在有切榜或多榜單的比賽中,可能存在榜單排名激烈震動的情況,例如下面這個例子:Data Science Bowl 2017我們看到,第一名是從公榜上升了130多名,而第5名則上升了349。公榜結(jié)果就是好的模型私榜不一定就好,因為Kaggle是模擬real world的時刻在變化的數(shù)據(jù),不一定遵從過去的規(guī)律,用過去的數(shù)據(jù)是無法確定就能預(yù)測未來的。一般情況下shake的原因可以歸為如下幾種:1.數(shù)據(jù)不同分布2.數(shù)據(jù)量太小3.異常值影響較大4.metric過于敏感5.模型太接近6.overfit等。那么第一名中的模型與第二名中的模型之間有什么區(qū)別呢?如果你的答案是:“區(qū)別在于,第一款模型比第二型模型更好,因為它具有較小的損失”,那么這個回答就太倉促了。事實上:我們?nèi)绾尾拍艽_定測試集上更好的度量標(biāo)準(zhǔn)意味的是更好的模型,而不是一個更幸運的模型呢?
對于數(shù)據(jù)科學(xué)家來說,知道模型選擇中哪一部分是偶然發(fā)揮的作用是一項基本技能。在本文中,我們將說明如何量化選擇最佳模型過程中涉及的隨機性。什么是“最好模型”?
假設(shè)有兩個模型A和B,我們想選擇最好的一個。最好的模型是在看不見的數(shù)據(jù)上表現(xiàn)最好的模型,這個應(yīng)該是一個公認(rèn)的判斷方式。所以我們收集了一些測試數(shù)據(jù)(在訓(xùn)練期間沒有使用的),并在此基礎(chǔ)上評估我模型。假設(shè)模型A的ROC值為86%,模型B為85%。這是否意味著模型A比模型B更好?就目前我們掌握的信息而言:是的。但在一段時間之后,又收集了更多的數(shù)據(jù)并將其添加到測試集中。現(xiàn)在模型A仍然是86%,但模型B增加到87%。那么現(xiàn)在來說,B比A好了,對吧。對于一個給定的任務(wù),最好的模型是在所有可能的不可見數(shù)據(jù)上表現(xiàn)最好的模型。
這個定義的重要部分是“所有可能”。我們能夠訪問的數(shù)據(jù)是有限的,所以測試數(shù)據(jù)集只是所有可能的不可見數(shù)據(jù)的一小部分。這就像是說我們永遠(yuǎn)都不知道什么才是最好的模型!Universe
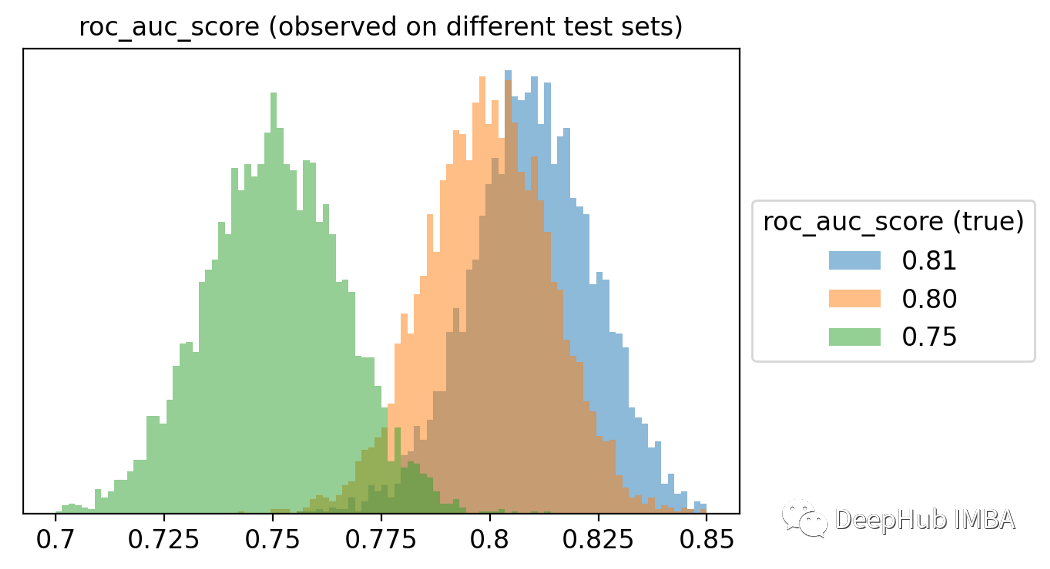
我們將將所有可能的看不見數(shù)據(jù)的集合稱為“Universe”。在現(xiàn)實世界中,我們永遠(yuǎn)無法觀察到完整的Universe,而只有一個從Universe中隨機采樣的測試數(shù)據(jù)集。模型的真正性能是其在Universe上的性能, 在這種情況下該模型的真實ROC得分為80.4%。但是我們永遠(yuǎn)無法觀察到Universe,我們永遠(yuǎn)無法觀察到模型的真實ROC。我們觀察到的是在測試集上計算的ROC分?jǐn)?shù)。有時它會更高(81.6%),有時會更低(79.9%和78.5%),但是我們無法知道真正的ROC分?jǐn)?shù)與觀察到的ROC得分有多遠(yuǎn)。我們所能做的就是嘗試評估該過程中涉及多少隨機性。為此需要模擬Universe并從中取樣許多隨機測試數(shù)據(jù)集。這樣我們就可以量化觀察到的分?jǐn)?shù)的離散度。如何模擬Universe?
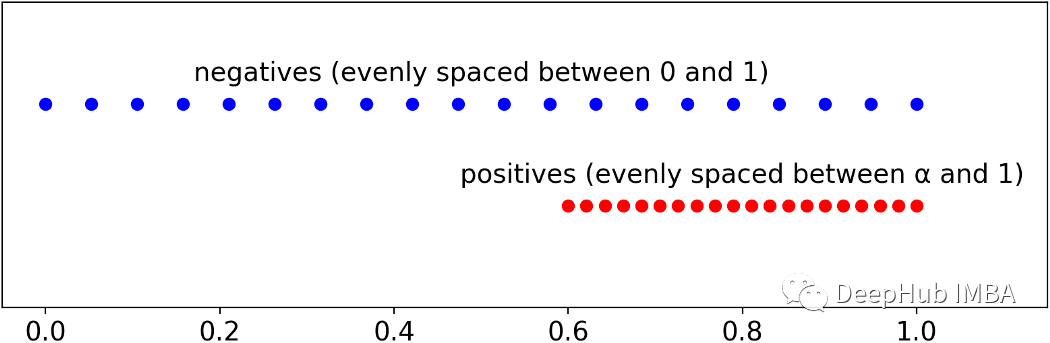
我們的目標(biāo)是獲得具有給定ROC評分的樣本(觀測結(jié)果),有一種非常簡單的方法可以做到這一點。首先需要設(shè)定的所需的個體數(shù)量(通常是一個很大的數(shù)字)。然后設(shè)置流行率prevalence(上面的例子是2分類問題,所以只有正負(fù)樣本),即陽性的百分比(可以將其保留為50%,這是默認(rèn)值)。第三步是選擇我們想要在Universe中的ROC分?jǐn)?shù)。最后可以計算Universe中每個個體的預(yù)測概率:負(fù)的必須在0和1之間均勻間隔,而正的必須在α和1之間均勻間隔。在Python中,使用以下函數(shù)實現(xiàn): def get_y_proba(roc, n=100000, prevalence=.5): n_ones = int(round(n * prevalence)) n_zeros = n - n_ones y = np.array([0] * n_zeros + [1] * n_ones) alpha = (roc - .5) * 2
proba_zeros = np.linspace(0, 1, n_zeros) proba_ones = np.linspace(alpha, 1, n_ones) proba = np.concatenate([proba_zeros, proba_ones])
return y, proba
獲取我們的不確定性
現(xiàn)在可以創(chuàng)建合成數(shù)據(jù)了,通過以下命令來獲取universe: y_universe, proba_universe = get_y_proba(roc=.8, n=100000, prevalence=.5)
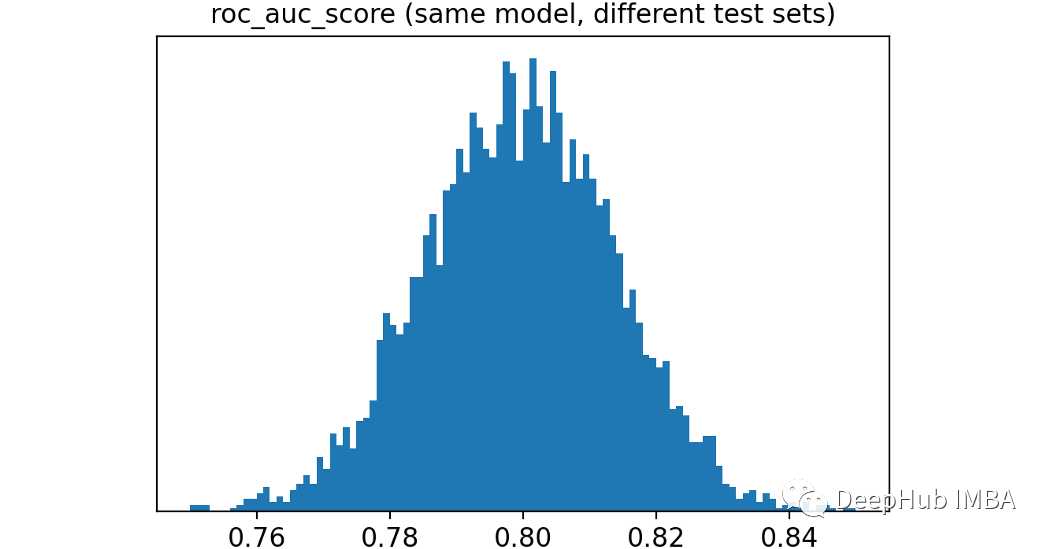
我們的全量數(shù)據(jù)(universe)是由10萬次觀測組成的,其中一半是真值的,ROC得分為80%。讓我們模擬不同測試集的提取。每次將提取5000個不同的測試集,每個測試集包含1000個觀測數(shù)據(jù)。這是相應(yīng)的代碼: rocs_sample = [] for i in range(5_000): index = np.random.choice(range(len(y_universe)), 1_000, replace=True) y_sample, proba_sample = y[index], proba[index] roc_sample = roc_auc_score(y_sample, proba_sample) rocs_sample.append(roc_sample)
可以看到結(jié)果是非常不同的,從低于76%到超過84%都會出現(xiàn)。在正常應(yīng)用中,我們選擇2個模型如下:一個ROC是78%,另一個是82%。他們有相同的潛在ROC,而這種差異只是偶然的結(jié)果的可能性有多大呢?為了給我們一個判斷的依據(jù),可以計算模擬中每對觀察到的ROC得分之間的距離。Scikit-learn有一個pairwise_distance函數(shù)可以實現(xiàn)這一點。 import numpy as np from sklearn.metrics import pairwise_distances
dist = pairwise_distances(np.array(rocs_sample).reshape(-1,1)) dist = dist[np.triu_indices(len(rocs_sample), k=1)]
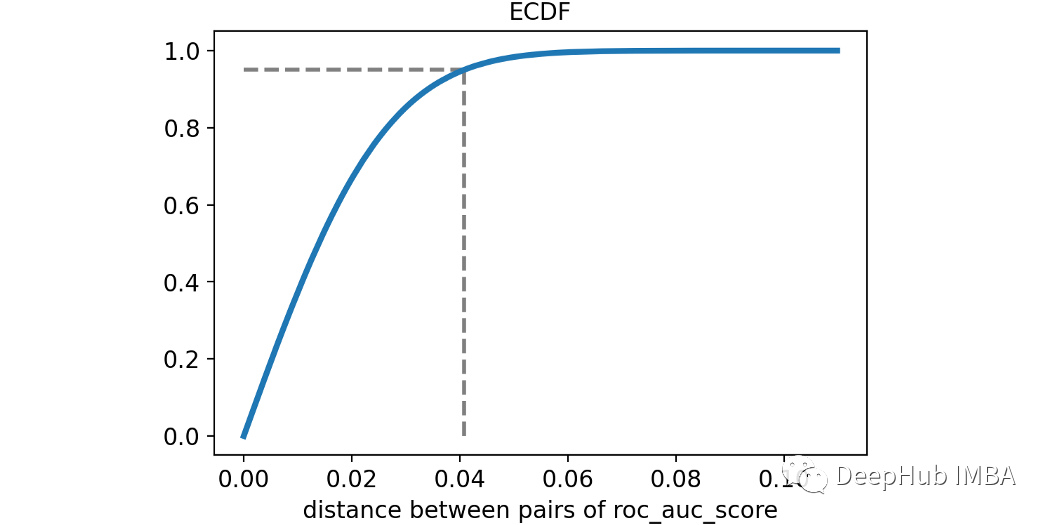
讓我們用經(jīng)驗累積分布函數(shù)來可視化ROC得分之間的兩兩距離。第95個百分位(用虛線突出顯示)約為4%。這意味著兩種模型(性能相同)之間的差異只有5%的時間大于4%。使用統(tǒng)計術(shù)語我們會說:小于4%的差異不顯著!這很有趣,因為通常我們會認(rèn)為82%的ROC模型比78%的ROC模型要好得多。為了獲得這個概念的另一個可視化,我模擬了三個不同的universe,一個的ROC值為75%,另一個為80%,最后一個為81%。這些是觀察到的ROC評分的分布。從上圖中可以明顯看出,最好的模型通常不會獲勝!想象一下,比較幾十個模型,每個模型的真實ROC得分都不同。也就是說選擇可能不是最好的模型。而是選擇了一個最幸運的。還能做點什么嗎?
上面的描述都說明了一個問題:沒有辦法100%確定一個模型比另一個更好,這聽起來像一場噩夢。當(dāng)然:在數(shù)據(jù)科學(xué)中不存在100%的確定性,但是我們還是有一些小小的技巧。選擇最佳模型的不確定性程度既取決于universe的特征,也取決于從universe中提取的測試集的特征。這里有三個參數(shù)控制著不確定性:- 真實ROC:在universe中計算的ROC得分(這個肯定是得不到的,所以只能假設(shè))。
- 樣本流行率(prevalence):測試集中的陽性百分比。
為了了解這些元素對不確定性的影響,可以嘗試每個元素的不同值來模擬發(fā)生的情況:- 樣本數(shù):1000,5000和10000。
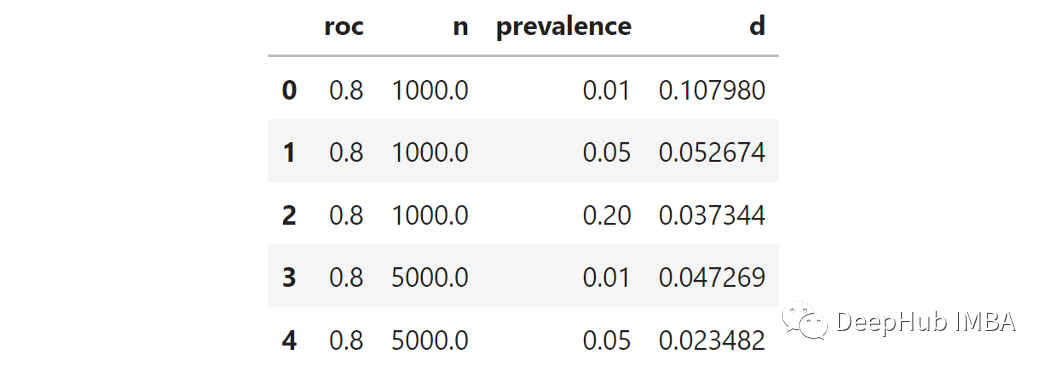
因為我們要為三個參數(shù)嘗試三個值,這意味著27種可能的組合。對于每個組合,我都可以使用上面的函數(shù)創(chuàng)建模擬universe,然后采樣了1000個不同的測試集,并測量了各自的ROC得分。然后計算1000個ROC得分的距離矩陣。最后取距離的第95個百分位數(shù)(從現(xiàn)在開始稱為“d”)。這就是上面所說的,對選擇模型的不確定性的衡量。
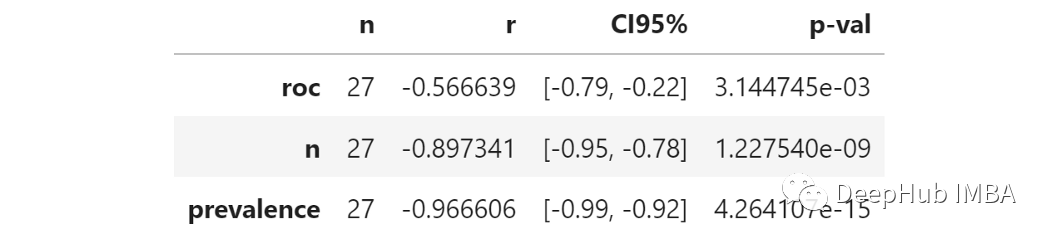
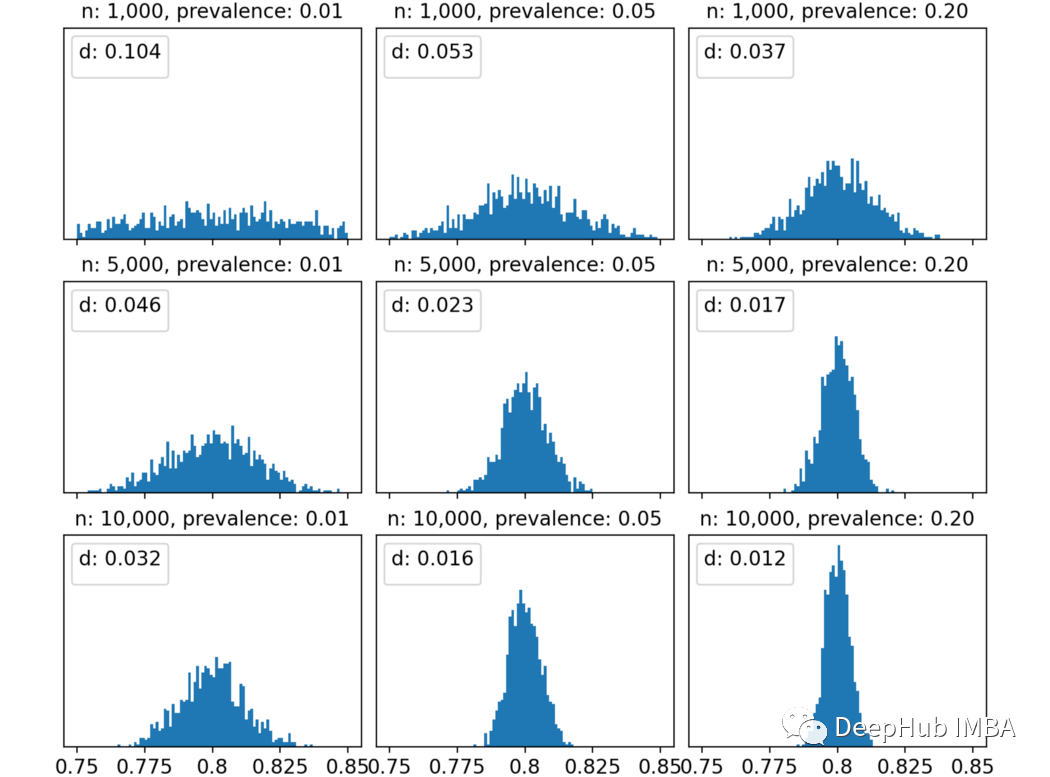
我們用95百分位測量不確定性。這個數(shù)字越高,ROC曲線比較的不確定性就越高。由于我們想知道不確定性如何取決于3個參數(shù),那么測量每個參數(shù)和“ D”之間的相關(guān)性能代表什么呢?這就是結(jié)果:稱為“ R”的列顯示了每個參數(shù)和不確定性之間的部分相關(guān)性。所有相關(guān)系數(shù)均為陰性,表明增加了這三個中的任何一個都會降低不確定性。真實ROC:全量數(shù)據(jù)中的ROC得分較高意味著不確定性較小。這是有道理的,因為根據(jù)定義,更高的ROC意味著較小程度的不確定性。樣本數(shù):增加樣品數(shù)會可降低不確定性。這很明顯,并且在統(tǒng)計數(shù)據(jù)中一直存在。樣本流行率:增加流行率會降低不確定性。較小的流行率意味著更少的陽性。更少的陽性意味著在抽樣時隨機性的權(quán)重更大, 因此有更大的不確定性。出于好奇心,對于固定的真實ROC(在這種情況下為80%)時,當(dāng)改變樣本數(shù)和樣本流行率時,我們看看得到的ROC分?jǐn)?shù)的分布。我認(rèn)為這張圖很明顯。以左上角為例:樣本數(shù)和流行率都非常小,我們有1000個觀察結(jié)果和1%的陽性結(jié)果,這意味著10個陽性結(jié)果和990個陰性結(jié)果,在這種情況下不確定性非常高,得到的ROC評分分布幾乎是均勻的,從75%到85%。ROC評分之間的距離的第95百分位數(shù)為10%,這意味著觀察到的ROC值為75%與觀察到的ROC值為85%之間沒有顯著差異。然而隨著逐步提高樣本維度數(shù)/或流行率,觀察到的ROC評分分布越來越集中在真實值附近(本例中為80%)。例如,10000樣本和20%的流行率,第95個百分位數(shù)變成了更合理的1.2%。這對我有用嗎?
應(yīng)該會有一點用,因為我們要知道在哪些條件下模型的結(jié)果在統(tǒng)計上是合理的。例如重復(fù)像在上面看到模擬會幫助你知道測試集的數(shù)值和流行率是否足以檢測模型性能之間的真正差異。如果還是無法模擬的話,那就Trust your CV 吧,其實我們的CV也降低了我們模型的隨機性。