漫畫：什么是時(shí)間復(fù)雜度？

時(shí)間復(fù)雜度是學(xué)習(xí)算法的基石，今天我們來(lái)聊聊為什么要引入時(shí)間復(fù)雜度，什么是時(shí)間復(fù)雜度以及如何去算一個(gè)算法的時(shí)間復(fù)雜度

一、刻畫算法的運(yùn)行時(shí)間

某日，慧能叫來(lái)了一塵打算給他補(bǔ)習(xí)補(bǔ)習(xí)一下基礎(chǔ)知識(shí)，只見(jiàn)克寫了一段非常簡(jiǎn)單的代碼

一塵看老師有點(diǎn)生氣，開(kāi)始虛心請(qǐng)教了

為了方便討論，這里我們把每一條語(yǔ)句的執(zhí)行時(shí)間都看做是一樣的，記為一個(gè)時(shí)間單元

① 藍(lán)色框的兩條語(yǔ)句，花費(fèi)兩個(gè)時(shí)間單元

②黑色框的一條語(yǔ)句，花費(fèi)n+1個(gè)時(shí)間單元

③紅色框的兩條語(yǔ)句，花費(fèi)2*n個(gè)時(shí)間單元

這不是數(shù)學(xué)嗎，一塵心里想到

其中的n被我們稱為問(wèn)題的規(guī)模，其實(shí)就是你處理問(wèn)題的大小

慧能順手畫了這個(gè)函數(shù)的圖

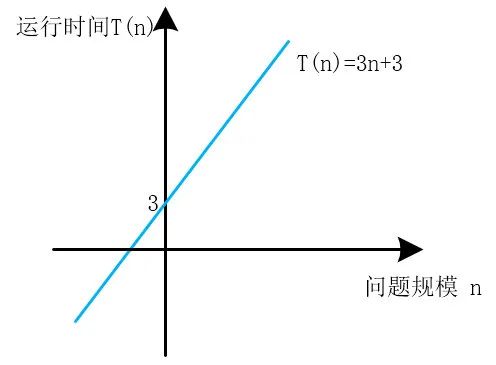
本文主要討論問(wèn)題規(guī)模和運(yùn)行時(shí)間的關(guān)系，假定不同輸入和運(yùn)行時(shí)間基本無(wú)關(guān)

二、時(shí)間復(fù)雜度

比如說(shuō)：T(n)=3n+3, 當(dāng)n非常大的時(shí)候常數(shù)3和n的系數(shù)3對(duì)函數(shù)結(jié)果的影響就很小了

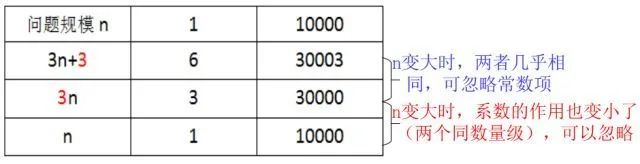
比如：

T(n)=n+1 忽略常數(shù)項(xiàng) T(n)~n

T(n)=n+n^2 忽略低階項(xiàng) T(n)~n^2

T(n)=3n 忽略最高階的系數(shù) T(n)~n

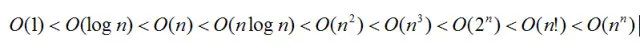
還好不用掌握那頭疼的數(shù)學(xué)，一塵心中想到

一塵把話題又拉了回來(lái)

更準(zhǔn)確地說(shuō)O代表了運(yùn)行時(shí)間函數(shù)的一個(gè)漸進(jìn)上界，即T(n)在數(shù)量級(jí)上小于等于f(n)

三、時(shí)間復(fù)雜度的計(jì)算

一、得出運(yùn)行時(shí)間的函數(shù)               二、對(duì)函數(shù)進(jìn)行簡(jiǎn)化

①用常數(shù)1來(lái)取代運(yùn)行時(shí)間中所有加法常數(shù)

②修改后的函數(shù)中，只保留最高階項(xiàng)      ③如果最高階項(xiàng)存在且不是1，則忽略這個(gè)項(xiàng)的系數(shù)

O(1)也被稱為常數(shù)階

一塵隨手寫了一段嵌套循環(huán)的代碼

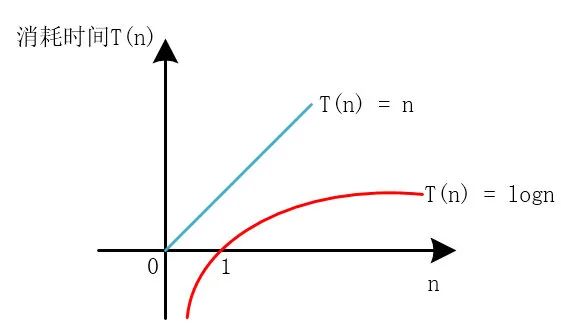
接著，慧能又寫了一段時(shí)間復(fù)雜度為對(duì)數(shù)的代碼

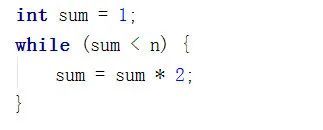
一向數(shù)學(xué)不太好的一塵此時(shí)有點(diǎn)懵