梯度下降是門手藝活

本文收錄在無痛的機(jī)器學(xué)習(xí)第一季（https://zhuanlan.zhihu.com/p/22464594）。

機(jī)器學(xué)習(xí)所涉及的內(nèi)容實(shí)在是太多了，于是我決定挑個(gè)軟柿子捏起，從最基礎(chǔ)的一個(gè)優(yōu)化算法開始聊起。這個(gè)算法就是梯度下降法，英文Gradient Descent。

什么是梯度下降法

作為大眾耳熟能詳?shù)膬?yōu)化算法，梯度下降法受到的關(guān)注不要太多。梯度下降法極易理解，但凡學(xué)過一點(diǎn)數(shù)學(xué)的童鞋都知道，梯度方向表示了函數(shù)增長速度最快的方向，那么和它相反的方向就是函數(shù)減少速度最快的方向了。對(duì)于機(jī)器學(xué)習(xí)模型優(yōu)化的問題，當(dāng)我們需要求解最小值的時(shí)候，朝著梯度下降的方向走，就能找到最優(yōu)值了。

那么具體來說梯度下降的算法怎么實(shí)現(xiàn)呢？我們先來一個(gè)最簡單的梯度下降算法，最簡單的梯度下降算法由兩個(gè)函數(shù)，三個(gè)變量組成：

函數(shù)1：待求的函數(shù)

函數(shù)2：待求函數(shù)的導(dǎo)數(shù)

變量1：當(dāng)前找到的變量，這個(gè)變量是“我們認(rèn)為”當(dāng)前找到的最好的變量，可以是函數(shù)達(dá)到最優(yōu)值（這里是最小值）。

變量2：梯度，對(duì)于絕大多數(shù)的函數(shù)來說，這個(gè)就是函數(shù)的負(fù)導(dǎo)數(shù)。

變量3：步長，也就是沿著梯度下降方向行進(jìn)的步長。也是這篇文章的主角。

我們可以用python寫出一個(gè)最簡單的梯度下降算法：

def gd(x_start, step, g):   # gd代表了Gradient Descent    x = x_start    for i in range(20):        grad = g(x)        x -= grad * step        print '[ Epoch {0} ] grad = {1}, x = {2}'.format(i, grad, x)        if abs(grad) < 1e-6:            break;    return x
關(guān)于python的語法在此不再贅述了，看不懂得童鞋自己想辦法去補(bǔ)課吧。

優(yōu)雅的步長

好了，算法搞定了，雖然有點(diǎn)粗糙，但是對(duì)于一些問題它是可以用的。我們用一個(gè)簡單到爆的例子來嘗試一下：

def f(x):    return x * x - 2 * x + 1
def g(x):    return 2 * x - 2

這個(gè)函數(shù)f(x)就是大家在中學(xué)喜聞樂見的，大家一眼就可以看出，最小值是x=1，這是函數(shù)值為0。為了防止大家對(duì)這個(gè)函數(shù)沒有感覺（真不應(yīng)該沒感覺啊……）我們首先把圖畫出來看一下：

import numpy as npimport matplotlib.pyplot as pltx = np.linspace(-5,7,100)y = f(x)plt.plot(x,?y)
然后我們就看到了：

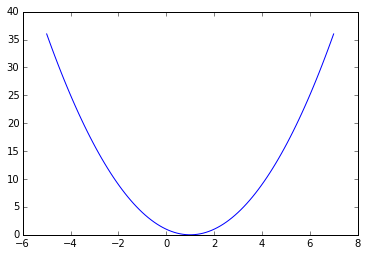
一個(gè)很簡單的拋物線的函數(shù)有木有？x=1是最小點(diǎn)有木有？

來讓我用梯度下降法計(jì)算一下：

gd(5,0.1,g)
于是我們得到了下面的輸出：

[ Epoch 0 ] grad = 8, x = 4.2
[ Epoch 1 ] grad = 6.4, x = 3.56
[ Epoch 2 ] grad = 5.12, x = 3.048
[ Epoch 3 ] grad = 4.096, x = 2.6384
[ Epoch 4 ] grad = 3.2768, x = 2.31072
[ Epoch 5 ] grad = 2.62144, x = 2.048576
[ Epoch 6 ] grad = 2.097152, x = 1.8388608
[ Epoch 7 ] grad = 1.6777216, x = 1.67108864
[ Epoch 8 ] grad = 1.34217728, x = 1.536870912
[ Epoch 9 ] grad = 1.073741824, x = 1.4294967296
[ Epoch 10 ] grad = 0.8589934592, x = 1.34359738368
[ Epoch 11 ] grad = 0.68719476736, x = 1.27487790694
[ Epoch 12 ] grad = 0.549755813888, x = 1.21990232556
[ Epoch 13 ] grad = 0.43980465111, x = 1.17592186044
[ Epoch 14 ] grad = 0.351843720888, x = 1.14073748836
[ Epoch 15 ] grad = 0.281474976711, x = 1.11258999068
[ Epoch 16 ] grad = 0.225179981369, x = 1.09007199255
[ Epoch 17 ] grad = 0.180143985095, x = 1.07205759404
[ Epoch 18 ] grad = 0.144115188076, x = 1.05764607523
[ Epoch 19 ] grad = 0.115292150461, x = 1.04611686018

可以看到，經(jīng)過20輪迭代，我們從初始值x=5不斷地逼近x=1，雖然沒有完全等于，但是在后面的迭代中它會(huì)不斷地逼近的。

好像我們已經(jīng)解決了這個(gè)問題，感覺有點(diǎn)輕松啊。高興之余，突然回過神來，那個(gè)步長我設(shè)的好像有點(diǎn)隨意啊，迭代了20輪還沒有完全收斂，是不是我太保守了，設(shè)得有點(diǎn)小？俗話說的好，人有多大膽，地有多大產(chǎn)。咱們設(shè)個(gè)大點(diǎn)的數(shù)字，讓它一步到位！（豪邁的表情）

gd(5,100,g)
這回設(shè)得夠大了，來看看結(jié)果：

[ Epoch 0 ] grad = 8, x = -795
[ Epoch 1 ] grad = -1592, x = 158405
[ Epoch 2 ] grad = 316808, x = -31522395
[ Epoch 3 ] grad = -63044792, x = 6272956805
[ Epoch 4 ] grad = 12545913608, x = -1248318403995
[ Epoch 5 ] grad = -2496636807992, x = 248415362395205
[ Epoch 6 ] grad = 496830724790408, x = -49434657116645595
[ Epoch 7 ] grad = -98869314233291192, x = 9837496766212473605
[ Epoch 8 ] grad = 19674993532424947208, x = -1957661856476282247195
[ Epoch 9 ] grad = -3915323712952564494392, x = 389574709438780167192005
[ Epoch 10 ] grad = 779149418877560334384008, x = -77525367178317253271208795
[ Epoch 11 ] grad = -155050734356634506542417592, x = 15427548068485133400970550405
[ Epoch 12 ] grad = 30855096136970266801941100808, x = -3070082065628541546793139530395
[ Epoch 13 ] grad = -6140164131257083093586279060792, x = 610946331060079767811834766548805
[ Epoch 14 ] grad = 1221892662120159535623669533097608, x = -121578319880955873794555118543211995
[ Epoch 15 ] grad = -243156639761911747589110237086423992, x = 24194085656310218885116468590099187205
[ Epoch 16 ] grad = 48388171312620437770232937180198374408, x = -4814623045605733558138177249429738253595
[ Epoch 17 ] grad = -9629246091211467116276354498859476507192, x = 958109986075540978069497272636517912465605
[ Epoch 18 ] grad = 1916219972151081956138994545273035824931208, x = -190663887229032654635829957254667064580655195
[ Epoch 19 ] grad = -381327774458065309271659914509334129161310392, x = 37942113558577498272530161493678745851550384005

我去，這是什么結(jié)果！不但沒有收斂，反而數(shù)字越來越大！這是要把python的數(shù)字撐爆的節(jié)奏啊！（實(shí)際上python的數(shù)字沒這么容易撐爆的……）

需要冷靜一下……為什么會(huì)出現(xiàn)這樣的情況？不是說好了是梯度下降么？怎么還會(huì)升上去？這個(gè)問題就要回到梯度這個(gè)概念本身來。

實(shí)際上梯度指的是在當(dāng)前變量處的梯度，對(duì)于這一點(diǎn)來說，它的梯度方向是這個(gè)方向，我們也可以利用泰勒公式證明在一定的范圍內(nèi)，沿著這個(gè)梯度方向走函數(shù)值是會(huì)下降的。但是，從函數(shù)中也可以看出，如果一步邁得太大，會(huì)跳出函數(shù)值下降的范圍，反而會(huì)使函數(shù)值越變越大，造成悲劇。

如何避免這種悲劇發(fā)生呢？簡單的方法就是將步長減少，像我們前面那樣設(shè)得小點(diǎn)。另外，還有一些Line-search的方法可以避免這樣的事情發(fā)生，這些方法以后有機(jī)會(huì)在慢慢聊。

現(xiàn)在，我們要鎮(zhèn)定一下，看樣子我們只能通過修改步長來完成這個(gè)問題了。這時(shí)候我們可以開一個(gè)腦洞：既然小步長會(huì)讓優(yōu)化問題收斂，大步長會(huì)讓優(yōu)化問題發(fā)散，那么有沒有一個(gè)步長會(huì)讓優(yōu)化問題原地打轉(zhuǎn)呢？

我們還是從x=5出發(fā)，假設(shè)經(jīng)過一輪迭代，我們求出了另一個(gè)x值，再用這個(gè)值迭代，x值又回到了5。我們用中學(xué)的數(shù)學(xué)能力建一個(gè)方程出來：

x=5, g(x)=8, 新的值x'=5 - 8 * step
g(x')=2 * (5-8*step) - 2，回到過去：x' - g(x') * step = x = 5
合并公式求解得，step=1

也就是說step=1時(shí)，求解會(huì)原地打轉(zhuǎn)，趕緊試一下：

gd(5,1,g)

[ Epoch 0 ] grad = 8, x = -3
[ Epoch 1 ] grad = -8, x = 5
[ Epoch 2 ] grad = 8, x = -3
[ Epoch 3 ] grad = -8, x = 5
[ Epoch 4 ] grad = 8, x = -3
[ Epoch 5 ] grad = -8, x = 5
[ Epoch 6 ] grad = 8, x = -3
[ Epoch 7 ] grad = -8, x = 5
[ Epoch 8 ] grad = 8, x = -3
[ Epoch 9 ] grad = -8, x = 5
[ Epoch 10 ] grad = 8, x = -3
[ Epoch 11 ] grad = -8, x = 5
[ Epoch 12 ] grad = 8, x = -3
[ Epoch 13 ] grad = -8, x = 5
[ Epoch 14 ] grad = 8, x = -3
[ Epoch 15 ] grad = -8, x = 5
[ Epoch 16 ] grad = 8, x = -3
[ Epoch 17 ] grad = -8, x = 5
[ Epoch 18 ] grad = 8, x = -3
[ Epoch 19 ] grad = -8, x = 5

果然不出我們所料，打轉(zhuǎn)了……

好了，現(xiàn)在我們基本明白了，當(dāng)步長大于1會(huì)出現(xiàn)求解發(fā)散，而小于1則不會(huì)，那么對(duì)于別的初始值，這個(gè)規(guī)則適用么？

gd(4,1,g)

[ Epoch 0 ] grad = 6, x = -2
[ Epoch 1 ] grad = -6, x = 4
[ Epoch 2 ] grad = 6, x = -2
[ Epoch 3 ] grad = -6, x = 4
[ Epoch 4 ] grad = 6, x = -2
[ Epoch 5 ] grad = -6, x = 4
[ Epoch 6 ] grad = 6, x = -2
[ Epoch 7 ] grad = -6, x = 4
[ Epoch 8 ] grad = 6, x = -2
[ Epoch 9 ] grad = -6, x = 4
[ Epoch 10 ] grad = 6, x = -2
[ Epoch 11 ] grad = -6, x = 4
[ Epoch 12 ] grad = 6, x = -2
[ Epoch 13 ] grad = -6, x = 4
[ Epoch 14 ] grad = 6, x = -2
[ Epoch 15 ] grad = -6, x = 4
[ Epoch 16 ] grad = 6, x = -2
[ Epoch 17 ] grad = -6, x = 4
[ Epoch 18 ] grad = 6, x = -2
[ Epoch 19 ] grad = -6, x = 4

果然試用，這樣一來，我們可以“認(rèn)為”，對(duì)于這個(gè)優(yōu)化問題，采用梯度下降法，對(duì)于固定步長的算法，步長不能超過1，不然問題會(huì)發(fā)散！

好了，下面我們換一個(gè)函數(shù)：，對(duì)于這個(gè)問題，它的安全閾值是多少呢？不羅嗦了，是0.25：

def f2(x):    return 4 * x * x - 4 * x + 1def g2(x):    return 8 * x - 4gd(5,0.25,g2)

[ Epoch 0 ] grad = 36, x = -4.0
[ Epoch 1 ] grad = -36.0, x = 5.0
[ Epoch 2 ] grad = 36.0, x = -4.0
[ Epoch 3 ] grad = -36.0, x = 5.0
[ Epoch 4 ] grad = 36.0, x = -4.0
[ Epoch 5 ] grad = -36.0, x = 5.0
[ Epoch 6 ] grad = 36.0, x = -4.0
[ Epoch 7 ] grad = -36.0, x = 5.0
[ Epoch 8 ] grad = 36.0, x = -4.0
[ Epoch 9 ] grad = -36.0, x = 5.0
[ Epoch 10 ] grad = 36.0, x = -4.0
[ Epoch 11 ] grad = -36.0, x = 5.0
[ Epoch 12 ] grad = 36.0, x = -4.0
[ Epoch 13 ] grad = -36.0, x = 5.0
[ Epoch 14 ] grad = 36.0, x = -4.0
[ Epoch 15 ] grad = -36.0, x = 5.0
[ Epoch 16 ] grad = 36.0, x = -4.0
[ Epoch 17 ] grad = -36.0, x = 5.0
[ Epoch 18 ] grad = 36.0, x = -4.0
[ Epoch 19 ] grad = -36.0, x = 5.0

好了，這個(gè)故事講完了。為什么要講這個(gè)故事呢？

這個(gè)故事說明了梯度下降法簡單中的不簡單（劃重點(diǎn)啊），雖然和的一些方法比起來在尋找優(yōu)化方向上比較輕松，可是這個(gè)步長真心需要點(diǎn)技巧，即使這樣一個(gè)一維的優(yōu)化問題都有這些問題，對(duì)于現(xiàn)在大火的深度學(xué)習(xí)，CNN優(yōu)化（沒錯(cuò)，說得就是你），一個(gè)base_lr基礎(chǔ)學(xué)習(xí)率+gamma學(xué)習(xí)衰減率真的可以輕松跳過像上面這樣的坑么？說實(shí)話還是需要一定的嘗試才能找到感覺。

最后多說一句，對(duì)于上面的一元二次函數(shù)，有沒有發(fā)現(xiàn)步長閾值和二階導(dǎo)數(shù)的關(guān)系呢？

本文的全部代碼可以在https://github.com/hsmyy/zhihuzhuanlan/blob/master/gd.ipynb閱覽。