分享一個(gè)Pandas應(yīng)用實(shí)戰(zhàn)案例——使用Python實(shí)現(xiàn)根據(jù)關(guān)系進(jìn)行分組

迎新年，GPT-4 Plus賬號(hào)大大降價(jià)了！

一、前言

近日，有群友提出這樣的問(wèn)題：

群友提示可以使用ChatGPT，并給出代碼：

二、實(shí)現(xiàn)過(guò)程

這里【瑜亮老師】給出了另外一個(gè)答案，與此同時(shí)，根據(jù)需求，構(gòu)造數(shù)據(jù)，使用pandas也可以完成需求，代碼如下：

        
        import pandas as pd

data = [
    ['劉備', '關(guān)羽'], ['劉備', '張飛'],
    ['曹操', '夏侯'], ['張飛', '諸葛'],
    ['夏侯', '荀彧'], ['孫權(quán)', '魯肅']
]

df = pd.DataFrame(data, columns=['發(fā)起', '接收'])


# 創(chuàng)建一個(gè)空字典用于存儲(chǔ)人名與組別的映射關(guān)系
groups = {}

# 遍歷數(shù)據(jù)框的每一行
for _, row in df.iterrows():
    sender = row['發(fā)起']
    receiver = row['接收']

    # 檢查發(fā)起者是否已存在于映射關(guān)系中
    if sender not in groups:
        # 如果不存在，則將發(fā)起者添加到映射關(guān)系中，并分配一個(gè)新的組別
        group = max(groups.values()) + 1 if groups else 1
        groups[sender] = group

    # 檢查接收者是否已存在于映射關(guān)系中
    if receiver not in groups:
        # 如果不存在，則將接收者添加到映射關(guān)系中，并分配與發(fā)起者相同的組別
        group = groups[sender]
        groups[receiver] = group

# 根據(jù)人名與組別的映射關(guān)系更新數(shù)據(jù)框的'組別'列
df['組別'] = df['發(fā)起'].map(groups)
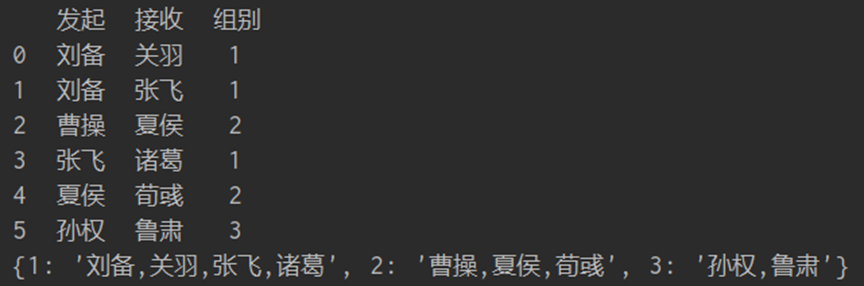
print(df)

# 同時(shí)可以將groups也用字典形式輸出
result = {}
for k, v in groups.items():
    if v not in result.keys():
        result[v] = k
    else:
        result[v] += "," + k
print(result)

      

運(yùn)行之后可以得到如下結(jié)果：

同時(shí)，根據(jù)大佬的提示，在python中這是典型的查找連通圖的問(wèn)題，直接的思路是使用現(xiàn)成的networkx包直接調(diào)用求解連通圖的算法即可，代碼如下：

        
        import networkx as nx

g = nx.Graph()
data = [
    ['劉備', '關(guān)羽'], ['劉備', '張飛'],
    ['曹操', '夏侯'], ['張飛', '諸葛'],
    ['夏侯', '荀彧'], ['孫權(quán)', '魯肅']
]
g.add_edges_from(data)

for sub_g in nx.connected_components(g):
    g_node = g.subgraph(sub_g).nodes()
    print(g_node)

      

代碼運(yùn)行后的結(jié)果如下：

使用networkx我們還可以將圖繪制出來(lái)：

        
        from matplotlib import pyplot as plt
import networkx as nx
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
g = nx.Graph()
data = [
    ['劉備', '關(guān)羽'],    ['劉備', '張飛'],
    ['曹操', '夏侯'],    ['張飛', '諸葛'],
    ['夏侯', '荀彧'],    ['孫權(quán)', '魯肅']
]
g.add_edges_from(data)
nx.draw_networkx(g)

      

代碼運(yùn)行后的結(jié)果如下：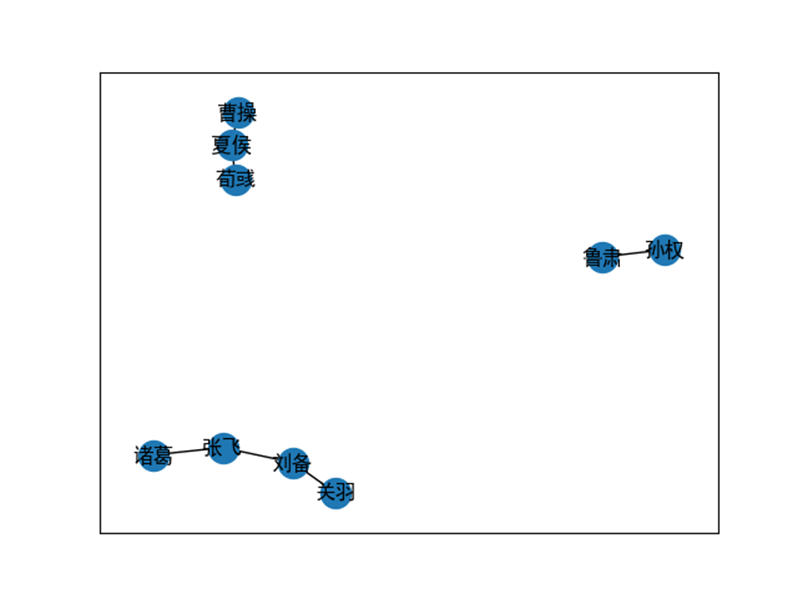

三、總結(jié)

這篇文章主要盤(pán)點(diǎn)了一個(gè)Pandas數(shù)據(jù)分析的問(wèn)題，文中針對(duì)該問(wèn)題，給出了具體的解析和代碼實(shí)現(xiàn)，幫助粉絲順利解決了問(wèn)題

GPT-4 Office 全家桶發(fā)布，我們的工作方式將永遠(yuǎn)改變！