查找算法常見的五大面試知識點與兩類實戰(zhàn)!
前言
查找(Search),又稱為搜索,指從數(shù)據(jù)表中找出符合特定條件的記錄。如今我們處在信息爆炸的大數(shù)據(jù)時代,如何從海量信息中快速找到需要的信息,這就需要查找技術。如果有什么不懂的或要查詢的,都會上網(wǎng)搜索一下,查找是最常見的應用之一。
本文解釋了查找的基本概念和查找算法的評價指標,闡述了靜態(tài)查找表的三種具體分類,以及應該如何查找哈希表,手把手教你如何解決查找沖突。最后作者結合Leetcode,帶你刷一刷查找常見題。

1. 查找的基本概念
查找也即檢索。首先,簡要說明在查找中涉及的術語。
文件:由記錄組成的集合,即含有大量數(shù)據(jù)的元素線性組合而成。
記錄:由若干數(shù)據(jù)項組成的數(shù)據(jù)元素,這些數(shù)據(jù)項也常稱作記錄中的數(shù)據(jù)域,用以表示某個狀態(tài)的物理意義。
關鍵字:用以區(qū)分文件中記錄的數(shù)據(jù)項的值。若此關鍵字可以惟一地標識一個記錄,則稱此關鍵字為主關鍵字。也就是說,對于不同的記錄,其對應的主關鍵字的值均不相同。若數(shù)據(jù)元素只有一個數(shù)據(jù)項,其關鍵字即為該數(shù)據(jù)元素的值。
查找是指根據(jù)給定的某個值,確定關鍵字值,查詢確定關鍵字值與給定值相等的記錄在文件中的位置。它是程序設計中一項重要的基本技術。查找的結果有兩種情況:若在文件中找到了待查找的記錄,則稱查找成功,這時可以得到該記錄在文件中的位置,或者得到該記錄中其他的信息;若在文件中沒有找到所需要的記錄,則稱查找不成功或查找失敗,這時,相應的查找算法給出查找失敗的信息,同時也得到記錄插入文件的位置。
如何進行查找?查找的方法很多,對不同的數(shù)據(jù)結構有不同的查找方法。例如,查電話號碼時,如果電話號碼簿是按用戶的姓名且以筆畫順序編排,則查找的方法是先順序查找待查用戶的所屬類別,然后在此類中再順序查找,直到找尋到用戶的電話號碼為止。又如,查英文單詞時,由于字典是按單詞的字母在字母表中的順序編排的,因此,查找時不需要從字典中第一個單詞開始比較,而只要根據(jù)待查單詞中每個字母在字母表中的位置查找該單詞。在設計相應的查找算法時,就是按以上的步驟進行的。
應當注意,在計算機中進行查找的方法是根據(jù)文件中的記錄是何種結構組織而確定的,對不同的結構應采用不同的查找方法。
查找算法的優(yōu)劣對計算機的應用效率影響很大,同樣的一個文件結構,選擇正確的、適合文件組織形式的查找方法可以極大地提高程序的運行速度。查找可分為靜態(tài)查找和動態(tài)查找兩種,在查找過程中不修改查找表的長度和表中內容的方法稱作靜態(tài)查找,反之稱作動態(tài)查找。
2. 查找算法的評價指標
關鍵字的平均比較次數(shù),也稱平均搜索長度ASL(Average Search Length):
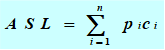
n:記錄的個數(shù) pi:查找第i個記錄的概率 ( 通常認為pi =1/n ) ci:找到第i個記錄所需的比較次數(shù)
3. 靜態(tài)查找表
3.1 順序查找
1)應用范圍:
順序表或線性鏈表表示的靜態(tài)查找表 表內元素之間無序
2)順序表的表示:
typedef struct {
ElemType *R; //表基址
int length; //表長
}SSTable;
3)順序查找的性能分析:
空間復雜度:一個輔助空間 時間復雜度: 查找成功時的平均查找長度(設表中各記錄查找概率相等):ASLs(n)=(1+2+ … +n)/n =(n+1)/2 查找不成功時的平均查找長度:ASLf =n+1
4)順序查找算法有特點
算法簡單,對表結構無任何要求(順序和鏈式)。 n很大時查找效率較低。 改進措施:非等概率查找時,可按照查找概率進行排序。
3.2 折半查找
1)算法思想:
設表長為n,low、high和mid分別指向待查元素所在區(qū)間的上界、下界和中點,k為給定值:
初始時,令low=1, high=n, mid=(low+high)/2 讓k與mid指向的記錄比較:若k = R[mid].key,查找成功 若k < R[mid].key,則high=mid-1 若k > R[mid].key,則low=mid+1 重復上述操作,直至low>high時,查找失敗
例如:
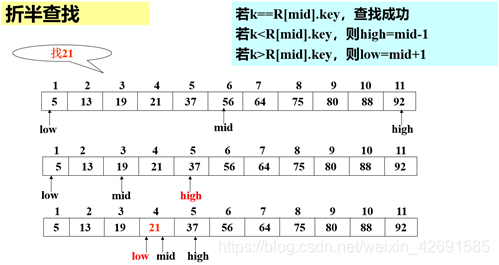
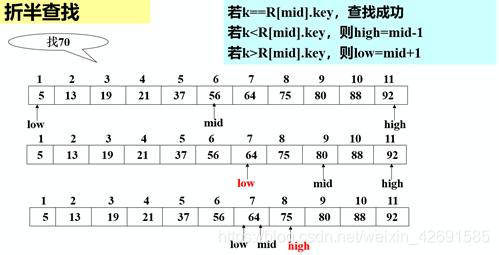
 2)折半查找的性能分析:
2)折半查找的性能分析:查找過程:每次將待查記錄所在區(qū)間縮小一半,比順序查找效率高,時間復雜度O(log2 n) 適用條件:采用順序存儲結構的有序表,不宜用于鏈式結構
3.3 分塊查找(塊間有序,塊內無序)
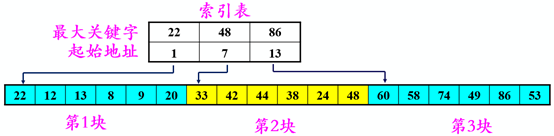
分塊有序,即分成若干子表,要求每個子表中的數(shù)值都比后一塊中數(shù)值小(但子表內部未必有序)。?然后將各子表中的最大關鍵字構成一個索引表,表中還要包含每個子表的起始地址(即頭指針)。
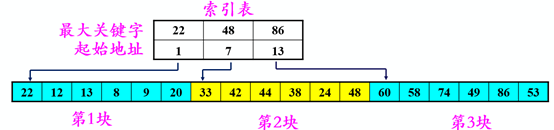 1)分塊查找過程:
1)分塊查找過程:對索引表使用折半查找法(因為索引表是有序表) 確定了待查關鍵字所在的子表后,在子表內采用順序查找法(因為各子表內部是無序表)
2)分塊查找優(yōu)缺點:
優(yōu)點:插入和刪除比較容易,無需進行大量移動。 缺點:要增加一個索引表的存儲空間并對初始索引表進行排序運算。 適用情況:若線性表既要快速查找又經(jīng)常動態(tài)變化,則可采用分塊查找
4. 哈希表的查找
4.1 理論基礎
1)基本思想:記錄的存儲位置與關鍵字之間存在對應關系:

優(yōu)點:查找速度極快O(1),查找效率與元素個數(shù)n無關。
例如:

查找方法:
根據(jù)哈希函數(shù)H(k)=k ,查找key=9,則訪問H(9)=9號地址,若內容為9,則成功。若查不到,則返回一個特殊值,如空指針或空記錄。
2)有關術語
哈希方法(雜湊法)
選取某個函數(shù),依該函數(shù)按關鍵字計算元素的存儲位置,并按此存放; 查找時,由同一個函數(shù)對給定關鍵值k計算地址,將k與地址單元中 元素關鍵碼進行比,確定查找是否成功
哈希函數(shù)(雜湊函數(shù)):哈希方法中使用的轉換函數(shù) 哈希表(雜湊表):按上述思想構造的表
 4.2 沖突解決
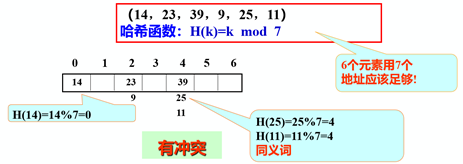
4.2 沖突解決當不同的關鍵碼映射到同一個哈希地址時,即沖突出現(xiàn):key1≠key2,但H(key1)=H(key2)。具有相同函數(shù)值的兩個關鍵字可以成為同義詞。
1)沖突現(xiàn)象舉例
 2)如何減少沖突
2)如何減少沖突實際上,沖突是不可能避免的:
 3)如何解決沖突:
3)如何解決沖突:開放定址法(開地址法)
其基本思想:有沖突時就去尋找下一個空的哈希地址,只要哈希表足夠大,空的哈希地址總能找到,并將數(shù)據(jù)元素存入。
步驟:
哈希函數(shù):
其中:m為哈希表長度,di 為增量序列
step1 取數(shù)據(jù)元素的關鍵字key,計算其哈希函數(shù)值(地址)。若該地址對應的存儲空間還沒有被占用,則將該元素存入;否則執(zhí)行step2解決沖突。 step2 根據(jù)選擇的沖突處理方法,計算關鍵字key的下一個存儲地址。若下一個存儲地址仍被占用,則繼續(xù)執(zhí)行step2,直到找到能用的存儲地址為止。

鏈地址法
基本思想:相同哈希地址的記錄鏈成一單鏈表,m個哈希地址就設m個單鏈表,然后用用一個數(shù)組將m個單鏈表的表頭指針存儲起來,形成一個動態(tài)的結構。
步驟:
優(yōu)點:
非同義詞不會沖突,無“聚集”現(xiàn)象 鏈表上結點空間動態(tài)申請,更適合于表長不確定的情況 取數(shù)據(jù)元素的關鍵字key,計算其哈希函數(shù)值(地址)。若該地址對應的鏈表為空,則將該元素插入此鏈表;
4.3 函數(shù)構造方法
1)哈希函數(shù)的構造方法
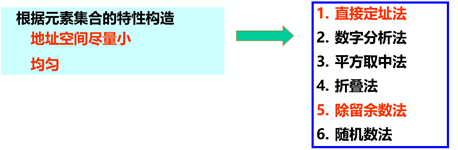 2)構造哈希函數(shù)考慮的因素
2)構造哈希函數(shù)考慮的因素執(zhí)行速度(即計算哈希函數(shù)所需時間) 關鍵字的長度 哈希表的大小 關鍵字的分布情況 查找頻率
4.4 哈希表的查找

哈希表的查找效率分析:
使用平均查找長度ASL來衡量查找算法,ASL取決于:
α 越大,表中記錄數(shù)越多,說明表裝得越滿,發(fā)生沖突的可能性就越大,查找時比較次數(shù)就越多。ASL與裝填因子α 有關!既不是嚴格的O(1),也不是O(n)。
哈希函數(shù) 處理沖突的方法 哈希表的裝填因子 
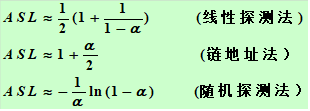
結論 對哈希表技術具有很好的平均性能,優(yōu)于一些傳統(tǒng)的技術 鏈地址法優(yōu)于開地址法 除留余數(shù)法作哈希函數(shù)優(yōu)于其它類型函數(shù)
5. 基本數(shù)據(jù)結構
第一類:查找有無–set
元素’a’是否存在,通常用set:集合 set只存儲鍵,而不需要對應其相應的值。 set中的鍵不允許重復 第二類:查找對應關系(鍵值對應)–dict
元素’a’出現(xiàn)了幾次:dict–>字典 dict中的鍵不允許重復 第三類:改變映射關系–map
通過將原有序列的關系映射統(tǒng)一表示為其他
6. 實戰(zhàn)1(查找表)
案例1:349 Intersection Of Two Arrays 1
【題目描述】
給定兩個數(shù)組nums,求兩個數(shù)組的公共元素。
如nums1 = [1,2,2,1],nums2 = [2,2]
結果為[2]
結果中每個元素只能出現(xiàn)一次
出現(xiàn)的順序可以是任意的
【解題思路】
由于每個元素只出現(xiàn)一次,因此不需要關注每個元素出現(xiàn)的次數(shù),用set的數(shù)據(jù)結構就可以了。記錄元素的有和無。
把nums1記錄為set,判斷nums2的元素是否在set中,是的話,就放在一個公共的set中,最后公共的set就是我們要的結果。
代碼如下:
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
nums1 = set(nums1)
return set([i for i in nums2 if i in nums1])
也可以通過set的內置方法來實現(xiàn),直接求set的交集:
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
set1 = set(nums1)
set2 = set(nums2)
return set2 & set1
1)解法1(哈希表:時間復雜度:O(m+n),空間復雜度:O(m))
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
hash_dict = {}
ans = []
for i in nums1:
if hash_dict.get(i) is None:
hash_dict[i] = 1
for j in nums2:
if hash_dict.get(j) is not None:
ans.append(j)
hash_dict[j] = None
return ans

2)解法2(遍歷,set函數(shù):時間復雜度:O(m+n),空間復雜度:O(m+n))
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
nums1 = set(nums1)
nums2 = set(nums2)
return nums1 & nums2
 案例2:350 Intersection Of Two Arrays 2
案例2:350 Intersection Of Two Arrays 2【題目描述】
給定兩個數(shù)組nums,求兩個數(shù)組的交集。
如nums1=[1,2,2,1],nums=[2,2]
結果為[2,2]
出現(xiàn)的順序可以是任意的
【解題思路】
元素出現(xiàn)的次數(shù)有用,那么對于存儲次數(shù)就是有意義的,所以選擇數(shù)據(jù)結構時,就應該選擇dict的結構,通過字典的比較來判斷;記錄每個元素的同時要記錄這個元素的頻次。
記錄num1的字典,遍歷nums2,比較nums1的字典的nums的key是否大于零,從而進行判斷。
代碼如下:
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
from collections import Counter
nums1_dict = Counter(nums1)
res = []
for num in nums2:
if nums1_dict[num] > 0:
# 說明找到了一個元素即在num1也在nums2
res.append(num)
nums1_dict[num] -= 1
return res
1)解法1(哈希表:時間復雜度:O(n+m),空間復雜度:O(n+m))
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
n1,n2=collections.Counter(nums1),collections.Counter(nums2)
res=[]
for i in n1:
tmp=min(n1[i],n2[i])
while tmp>0:
res.append(i)
tmp-=1
return res

2)解法2(字典)
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
nums1_map = collections.Counter(nums1)
nums2_map = collections.Counter(nums2)
res = []
for i,j in nums1_map.items():
if nums2_map.get(i):
res.extend([i]*min(j,nums2_map.get(i)))
return res

【題目描述】
給定兩個字符串 s 和 t ,編寫一個函數(shù)來判斷 t 是否是 s 的字母異位詞。
示例1:
輸入: s = "anagram", t = "nagaram"
輸出: true
示例 2:
輸入: s = "rat", t = "car"
輸出: false
【解題思路】
判斷異位詞即判斷變換位置后的字符串和原來是否相同,那么不僅需要存儲元素,還需要記錄元素的個數(shù)。可以選擇dict的數(shù)據(jù)結構,將字符串s和t都用dict存儲,而后直接比較兩個dict是否相同。
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
from collections import Counter
s = Counter(s)
t = Counter(t)
if s == t:
return True
else:
return False
1)解法1(哈希表:時間復雜度:O(n),空間復雜度:O(n))
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
dic = {}
for i in s:
if i not in dic:
dic[i] = 1
else:
dic[i] += 1
for j in t:
if j not in dic:
return False
else:
dic[j] -= 1
for val in dic.values():
if val != 0:
return False
return True

2)解法2(排序法:時間復雜度:O(nlogn),空間復雜度:o(1))
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t): return False
return True if sorted(s) == sorted(t) else False

案例4:202 Happy number
【題目描述】
編寫一個算法來判斷一個數(shù)是不是“快樂數(shù)”。
一個“快樂數(shù)”定義為:對于一個正整數(shù),每一次將該數(shù)替換為它每個位置上的數(shù)字的平方和,然后重復這個過程直到這個數(shù)變?yōu)?1,也可能是無限循環(huán)但始終變不到 1。如果可以變?yōu)?1,那么這個數(shù)就是快樂數(shù)。
示例:
輸入: 19
輸出: true
解釋:
1^2 + 9^2 = 82
8^2 + 2^2 = 68
6^2 + 8^2 = 100
1^2 + 0^2 + 0^2 = 1
【解題思路】
這道題目思路很明顯,當n不等于1時就循環(huán),每次循環(huán)時,將其最后一位到第一位的數(shù)依次平方求和,比較求和是否為1。
難點在于,什么時候跳出循環(huán)?
開始筆者的思路是,循環(huán)個100次,還沒得出結果就false,但是小學在算無限循環(huán)小數(shù)時有一個特征,就是當除的數(shù)中,和之前歷史的得到的數(shù)有重合時,這時就是無限循環(huán)小數(shù)。
那么這里也可以按此判斷,因為只需要判斷有或無,不需要記錄次數(shù),故用set的數(shù)據(jù)結構。每次對求和的數(shù)進行append,當新一次求和的值存在于set中時,就return false。
代碼如下:
class Solution:
def isHappy(self, n: int) -> bool:
already = set()
while n != 1:
sum = 0
while n > 0:
# 取n的最后一位數(shù)
tmp = n % 10
sum += tmp ** 2
# 將n的最后一位截掉
n //= 10
# 如果求的和在過程中出現(xiàn)過
if sum in already:
return False
else:
already.add(sum)
n = sum
return True
tips
#一般對多位數(shù)計算的套路是:
#循環(huán)從后向前取位數(shù)
while n >0 :
#取最后一位:
tmp = n % 10
#再截掉最后一位:
n = n // 10
1)解法1(快慢指針:時間復雜度:O(log n),空間復雜度:O(1))
class Solution:
def isHappy(self, n: int) -> bool:
f = lambda n: reduce(lambda x, y: x + y ** 2, (int(i) for i in str(n)), 0)
slow, fast = n, f(n)
while slow != fast:
slow = f(slow)
fast = f(f(fast))
if slow == 1 or fast == 1:
return True
return slow == 1

2)解法2(哈希表:時間復雜度:O(log n),空間復雜度:O(log n))
class Solution:
def isHappy(self, n: int) -> bool:
already = set()
while n != 1:
if n in already:
return False
already.add(n)
n = sum([int(x) * int(x) for x in str(n)])
return True

案例5:290 Word Pattern
【題目描述】
給出一個模式(pattern)以及一個字符串,判斷這個字符串是否符合模式。
示例1:
輸入: pattern = "abba",
str = "dog cat cat dog"
輸出: true
示例 2:
輸入:pattern = "abba",
str = "dog cat cat fish"
輸出: false
示例 3:
輸入: pattern = "aaaa", str = "dog cat cat dog"
輸出: false
示例 4:
輸入: pattern = "abba", str = "dog dog dog dog"
輸出: false
【解題思路】
抓住變與不變,筆者開始的思路是選擇了dict的數(shù)據(jù)結構,比較count值和dict對應的keys的個數(shù)是否相同,但是這樣無法判斷順序的關系,如測試用例:‘aba’,‘cat cat dog’。
那么如何能既考慮順序,也考慮鍵值對應的關系呢?
抓住變與不變,變的是鍵,但是不變的是各個字典中,對應的相同index下的值,如dict1[index] = dict2[index],那么我們可以創(chuàng)建兩個新的字典,遍歷index對兩個新的字典賦值,并比較value。
還有一個思路比較巧妙,既然不同,那么可以考慮怎么讓它們相同,將原來的dict通過map映射為相同的key,再比較相同key的dict是否相同。
代碼實現(xiàn)如下:
class Solution:
def wordPattern(self,pattern, str):
str = str.split()
return list(map(pattern.index,pattern)) == list(map(str.index,str))
tips
因為str是字符串,不是由單個字符組成,所以開始需要根據(jù)空格拆成字符list:
str = str.split()通過map將字典映射為index的list:
map(pattern.index, pattern)map是通過hash存儲的,不能直接進行比較,需要轉換為list比較list
1)解法1(哈希表:時間復雜度: O(n),空間復雜度: O(n))
class Solution:
def wordPattern(self, pattern: str, str: str) -> bool:
s = str.split()
if len(pattern) != len(s):
return False
dict1, dict2 = {}, {}
for i in range(len(pattern)):
if pattern[i] not in dict1 and s[i] not in dict2:
dict1[pattern[i]] = s[i]
dict2[s[i]] = pattern[i]
elif pattern[i] in dict1:
if dict1[pattern[i]] != s[i]:
return False
elif s[i] in dict2:
if dict2[s[i]] != pattern[i]:
return False
return True

案例6:205 Isomorphic Strings
【題目描述】
給定兩個字符串 s 和 t,判斷它們是否是同構的。
如果 s 中的字符可以被替換得到 t ,那么這兩個字符串是同構的。
所有出現(xiàn)的字符都必須用另一個字符替換,同時保留字符的順序。兩個字符不能映射到同一個字符上,但字符可以映射自己本身。
示例 1:
輸入: s = "egg", t = "add"
輸出: true
示例 2:
輸入: s = "foo", t = "bar"
輸出: false
示例 3:
輸入: s = "paper", t = "title"
輸出: true
【解題思路】
思路與上題一致,可以考慮通過建兩個dict,比較怎樣不同,也可以將不同轉化為相同。
直接用上題的套路代碼:
class Solution:
def isIsomorphic(self, s: str, t: str) -> bool:
return list(map(s.index,s)) == list(map(t.index,t))
1)解法1(哈希表:時間復雜度: O(n),空間復雜度: O(1))
class Solution:
def isIsomorphic(self, s: str, t: str) -> bool:
record = {}
if len(set(s))!=len(set(t)):
return False
for ss, tt in zip(s, t):
if ss not in record:
record[ss] = tt
else:
if record[ss] != tt:
return False
return True

2)解法2(字典)
class Solution:
def isIsomorphic(self, s: str, t: str) -> bool:
map1 = {}
map2 = {}
for i in range(len(s)):
if s[i] in map1 and t[i] != map1[s[i]]:
return False
if t[i] in map2 and s[i] != map2[t[i]]:
return False
map1[s[i]] = t[i]
map2[t[i]] = s[i]
return True

案例7:451 Sort Characters By Frequency
【題目描述】
給定一個字符串,請將字符串里的字符按照出現(xiàn)的頻率降序排列。
示例 1:
輸入:
"tree"
輸出:
"eert"
示例 2:
輸入:
"cccaaa"
輸出:
"cccaaa"
示例 3:
輸入:
"Aabb"
輸出:
"bbAa"
【解題思路】
對于相同頻次的字母,順序任意,需要考慮大小寫,返回的是字符串。
使用字典統(tǒng)計頻率,對字典的value進行排序,最終根據(jù)key的字符串乘上value次數(shù),組合在一起輸出。
class Solution:
def frequencySort(self, s: str) -> str:
from collections import Counter
s_dict = Counter(s)
# sorted返回的是列表元組
s = sorted(s_dict.items(), key=lambda item:item[1], reverse = True)
# 因為返回的是字符串
res = ''
for key, value in s:
res += key * value
return res
tips
通過sorted的方法進行value排序,對字典排序后無法直接按照字典進行返回,返回的為列表元組:
# 對value值由大到小排序
s = sorted(s_dict.items(), key=lambda item:item[1], reverse = True)
# 對key由小到大排序
s = sorted(s_dict.items(), key=lambda item:item[0])
輸出為字符串的情況下,可以由字符串直接進行拼接:
# 由key和value相乘進行拼接
's' * 5 + 'd'*2
1)解法1(字典:時間復雜度: O(nlogn),空間復雜度: O(n))
class Solution:
def frequencySort(self, s: str) -> str:
cnt = defaultdict(int)
for i in s:
cnt[i] += 1
ans = ""
for k, v in sorted(cnt.items(), key=lambda x: -x[1]):
ans += k * v
return ans
 2)解法2(Counter)
2)解法2(Counter)class Solution:
def frequencySort(self, s: str) -> str:
return "".join(k * v for k, v in collections.Counter(s).most_common())

7. 實戰(zhàn)2(二分查找)
7.1 理解
查找在算法題中是很常見的,但是怎么最大化查找的效率和寫出bugfree的代碼才是難的部分。一般查找方法有順序查找、二分查找和雙指針,推薦一開始可以直接用順序查找,如果遇到TLE的情況再考慮剩下的兩種,畢竟AC是最重要的。
一般二分查找的對象是有序或者由有序部分變化的(可能暫時理解不了,看例題即可),但還存在一種可以運用的地方是按值二分查找,之后會介紹。
7.2 代碼模板
總體來說二分查找是比較簡單的算法,網(wǎng)上看到的寫法也很多,掌握一種就可以了。以下是我的寫法,參考C++標準庫里的寫法。這種寫法比較好的點在于:
即使區(qū)間為空、答案不存在、有重復元素、搜索開/閉區(qū)間的上/下界也同樣適用 ±1 的位置調整只出現(xiàn)了一次,而且最后返回lo還是hi都是對的,無需糾結
class Solution:
def firstBadVersion(self, arr):
# 第一點
lo, hi = 0, len(arr)-1
while lo < hi:
# 第二點
mid = (lo+hi) // 2
# 第三點
if f(x):
lo = mid + 1
else:
hi = mid
return lo
解釋:
第一點:lo和hi分別對應搜索的上界和下界,但不一定為0和arr最后一個元素的下標。 第二點:因為Python沒有溢出,int型不夠了會自動改成long int型,所以無需擔心。如果再苛求一點,可以把這一行改成
mid = lo + (hi-lo) // 2
# 之所以 //2 這部分不用位運算 >> 1 是因為會自動優(yōu)化,效率不會提升
第三點:比較重要的就是這個f(x),在帶入模板的情況下,寫對函數(shù)就完了。
那么我們一步一步地揭開二分查找的神秘面紗,首先來一道簡單的題。
案例1:35. Search Insert Position
【題目描述】
給定排序數(shù)組和目標值,如果找到目標,則返回索引。如果不是,則返回按順序插入索引的位置的索引。您可以假設數(shù)組中沒有重復項。
Example 1:
Input: [1,3,5,6], 5
Output: 2
Example 2:
Input: [1,3,5,6], 2
Output: 1
Example 3:
Input: [1,3,5,6], 7
Output: 4
Example 4:
Input: [1,3,5,6], 0
Output: 0
【解題思路】
這里要注意的點是 high 要設置為 len(nums) 的原因是像第三個例子會超出數(shù)組的最大值,所以要讓 lo 能到 這個下標。
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
lo, hi = 0, len(nums)
while lo < hi:
mid = (lo + hi) // 2
if nums[mid] < target:
lo = mid + 1
else:
hi = mid
return lo
1)解法1(暴力破解:時間復雜度:O(N),空間復雜度:O(1))
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
n = len(nums)
for i in range(-1, n - 1):
if nums[i + 1] >= target:
return i + 1
return n

2)解法2(二分法:時間復雜度:O(logn),空間復雜度:O(1))
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
size = len(nums)
if size==0:
return 0
if nums[size-1] return size
left, right = 0, size-1
while left < right:
mid = (left + right) // 2
if nums[mid] < target:
left = mid + 1
else:
right = mid
return left
 案例2:540. Single Element in a Sorted Array
案例2:540. Single Element in a Sorted Array【題目描述】
您將獲得一個僅由整數(shù)組成的排序數(shù)組,其中每個元素精確出現(xiàn)兩次,但一個元素僅出現(xiàn)一次。找到只出現(xiàn)一次的單個元素。
Example
Example 1:
Input: [1,1,2,3,3,4,4,8,8]
Output: 2
Example 2:
Input: [3,3,7,7,10,11,11]
Output: 10
【解題思路】
異或的巧妙應用!如果mid是偶數(shù),那么和1異或的話,那么得到的是mid+1,如果mid是奇數(shù),得到的是mid-1。如果相等的話,那么唯一的元素還在這之后,往后找就可以了。
class Solution:
def singleNonDuplicate(self, nums):
lo, hi = 0, len(nums) - 1
while lo < hi:
mid = (lo + hi) // 2
if nums[mid] == nums[mid ^ 1]:
lo = mid + 1
else:
hi = mid
return nums[lo]
是不是還挺簡單哈哈,那我們來道HARD難度的題!
1)解法1(二分法:時間復雜度:O(logn),空間復雜度:O(n))
class Solution(object):
def singleNonDuplicate(self, nums):
l = 0
r = len(nums) - 1
while l < r:
mid = l + (r-l)//2
if mid % 2 == 1:
mid -= 1
if nums[mid] == nums[mid+1]:
l = mid + 2
else:
r = mid
return nums[l]

案例3:410. Split Array Largest Sum
【題目描述】
給定一個由非負整數(shù)和整數(shù)m組成的數(shù)組,您可以將該數(shù)組拆分為m個非空連續(xù)子數(shù)組。編寫算法以最小化這m個子數(shù)組中的最大和。
Example
Input:
nums = [7,2,5,10,8]
m = 2
Output:
18
Explanation:
There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8],
where the largest sum among the two subarrays is only 18.
【解題思路】
這其實就是二分查找里的按值二分了,可以看出這里的元素就無序了。但是我們的目標是找到一個合適的最小和,換個角度理解我們要找的值在最小值max(nums)和sum(nums)內,而這兩個值中間是連續(xù)的。是不是有點難理解,那么看代碼吧 輔助函數(shù)的作用是判斷當前的“最小和”的情況下,區(qū)間數(shù)是多少,來和m判斷 這里的下界是數(shù)組的最大值是因為如果比最大值小那么一個區(qū)間就裝不下,數(shù)組的上界是數(shù)組和因為區(qū)間最少是一個,沒必要擴大搜索的范圍
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
def helper(mid):
res = tmp = 0
for num in nums:
if tmp + num <= mid:
tmp += num
else:
res += 1
tmp = num
return res + 1
lo, hi = max(nums), sum(nums)
while lo < hi:
mid = (lo + hi) // 2
if helper(mid) > m:
lo = mid + 1
else:
hi = mid
return lo
1)解法1(二分法:時間復雜度:O(n*log(sum(nums)-max(nums))),空間復雜度:O(1))
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
lo, hi = 0, 0
for num in nums:
lo = max(lo, num)
hi += num
while lo < hi:
mid = lo + ((hi - lo) >> 1)
if self._count(nums, mid) > m:
lo = mid + 1
else:
hi = mid
return lo
def _count(self, nums, val):
count = 1
_sum = 0
for n in nums:
_sum += n
if _sum > val:
count += 1
_sum = n
return count

2)解法2(動態(tài)規(guī)劃:時間復雜度O(m_len(nums)),空間復雜度O(m_len(nums)))
class Solution:
def splitArray(self, nums: List[int], m: int) -> int:
from functools import lru_cache
n = len(nums)
def dfs(i, k):
if k == 1:
return sum(nums[i:])
res = float("inf")
cur = 0
for j in range(i, n):
cur += nums[j]
# 關鍵
if res <= cur:
break
res = min(res, max(cur, dfs(j + 1, k - 1)))
return res
return dfs(0, m)

【參考資料】
編程實踐(LeetCode 分類練習) 力扣(LeetCode)平臺
