厲害了！困擾數(shù)學(xué)家90年的猜想，被計算機搜索30分鐘解決了

本文經(jīng)AI新媒體量子位（ID：QbitAI）授權(quán)轉(zhuǎn)載，轉(zhuǎn)載請聯(lián)系出處

曉查 發(fā)自 凹非寺

數(shù)學(xué)家會代碼，就連困擾人類90年的數(shù)學(xué)猜想也擋不住。

來自斯坦福、CMU等高校的4名數(shù)學(xué)家，直接將一個數(shù)學(xué)難題轉(zhuǎn)化成了對10億個結(jié)果進行“暴力搜索”。

△?論文作者之一CMU助理教授Marijn Heule

他們把這串代碼輸入40臺電腦組成的計算集群，30分鐘后，計算機給出了一個200GB大小的證明結(jié)果：

凱勒猜想在不超過7維的空間上都是正確的。

現(xiàn)在，任何人都可以去GitHub上克隆這串代碼，驗證這一數(shù)學(xué)定理。

比較反轉(zhuǎn)的是，這段獲得計算機學(xué)術(shù)會議IJCAR（國際自動推理聯(lián)合會議）最佳論文獎的程序，上線GitHub半年，只攬獲了一顆星。

那么，這4位數(shù)學(xué)家要證明的“凱勒猜想”到底是什么？為何非要用計算機來證明？計算機證明的結(jié)果可靠嗎？

下面讓我們一一道來。

什么是凱勒猜想

假如用一批完全相同的正方形瓷磚鋪滿地面，中間不留空隙。顯然，瓷磚之間會共用一條邊，如下圖藍線所示：

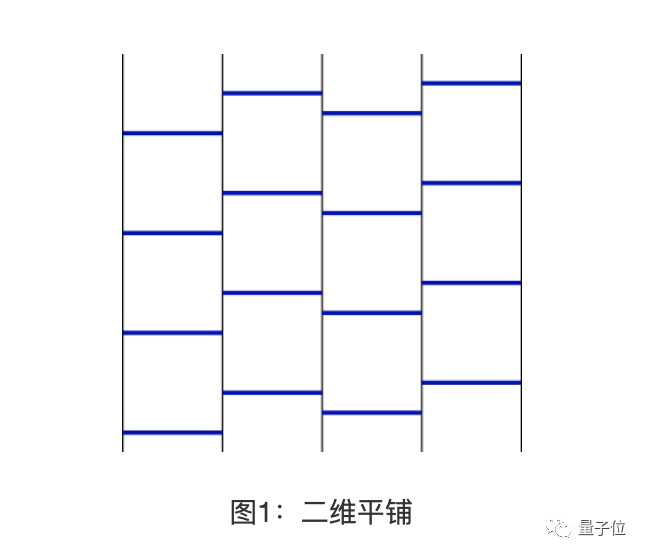
在3維空間中，如果要用立方體占滿空間，是不是也和2維空間類似呢？

想象一下，如果像下圖那樣在空間中隨便放入幾個立方體，由此展開填滿整個空間，那么唯一的辦法就是讓接上的立方體共用藍色的面。

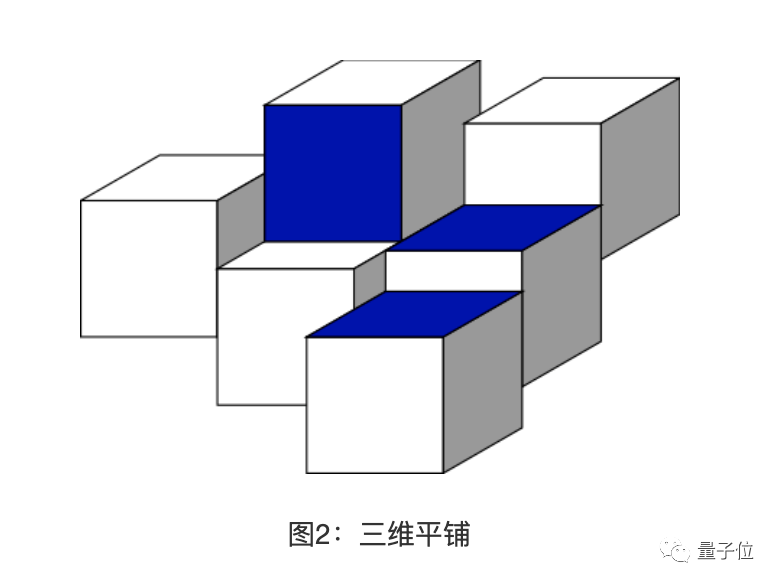
2維、3維皆如此，更高維度的空間會怎樣？

1930年，德國數(shù)學(xué)家凱勒猜測，如果用n維立方體填滿無限空間，則立方體之間必然會出現(xiàn)“面對面”，對于任意維度都成立。

這便是凱勒猜想。

但數(shù)學(xué)猜想不能僅靠直覺，必須有嚴格的證明。90年來，數(shù)學(xué)家一直不懈努力。

1940年，數(shù)學(xué)家Perron證明了凱勒猜想在1到6維空間是正確的。

1992年，另外兩位數(shù)學(xué)家Lagarias和Shor證明，凱勒猜想在10維空間上是錯誤的。

（注：這位Shor就是那個提出用量子計算機求解質(zhì)因數(shù)分解的Shor算法的數(shù)學(xué)家。）

非常不幸，凱勒猜想竟然是錯的！然而問題并沒有到此結(jié)束。

還有3個維度沒有解決呢！在7維、8維、9維三個維度空間中，凱勒猜想是否成立？

只要解決這三個維度，纏繞數(shù)學(xué)家?guī)资甑膯栴}就徹底搞定了。

數(shù)學(xué)論證表明，如果凱勒猜想在n維空間上是錯的，那么它在比n更高的維度上也一定是錯的。

2002年，數(shù)學(xué)家Mackey已證明，凱勒猜想在8維空間不成立，因此在9維空間也不成立。

至此，7維空間成為唯一的難題。

△?證明8維空間凱勒猜想錯誤的CMU教授Mackey

證明方法的改進

可能你已經(jīng)發(fā)現(xiàn)，從上世紀90年代以來，凱勒猜想的證明速度大大加快，數(shù)學(xué)家只用了10年時間就把問題縮小到三個維度。

這主要得益于兩位數(shù)學(xué)家的貢獻。

當年，Perron求解1到6維時，沒有特殊的捷徑。而到1990年，凱勒猜想的證明方法發(fā)生了巨大的變化。

數(shù)學(xué)家Corrádi和Szabó提出了一種新的思路，把原來無限空間的問題變成有限的、離散的問題，也讓計算機解決凱勒猜想成為可能。

他們巧妙地把凱勒猜想變成了圖論問題，就是構(gòu)造所謂的凱勒圖（Keller Graph），而圖論正是計算機所擅長的。

在這種方法的指導(dǎo)下，Lagarias和Shor兩人很快在2年后就證明了10維空間的情況：凱勒猜想不成立。又過了10年，Mackey證明，凱勒猜想在8維空間不成立。

那么，凱勒圖究竟是什么，它為什么能夠加速凱勒猜想的證明？

構(gòu)造“凱勒圖”

首先，我們從最簡單的2維情況說起。

現(xiàn)在，我們有一種牌，牌上畫著兩個有顏色的點。兩個點是有順序的，不能調(diào)換。比如，1黑2白≠1白2黑。

兩個點總共可以涂4種顏色，顏色分成2對：紅色對綠色、白色對黑色。

數(shù)學(xué)家已經(jīng)證明，分配給點的顏色相當于正方形在空間中的坐標。兩張牌的顏色是否配對表示兩個正方形的相對位置。

點的顏色與正方形的具體關(guān)系是這樣的：

1、兩對點完全相同，表示兩個正方形完全重疊

2、兩對點顏色都不同，且顏色都不配對，表示兩個正方形有部分重疊

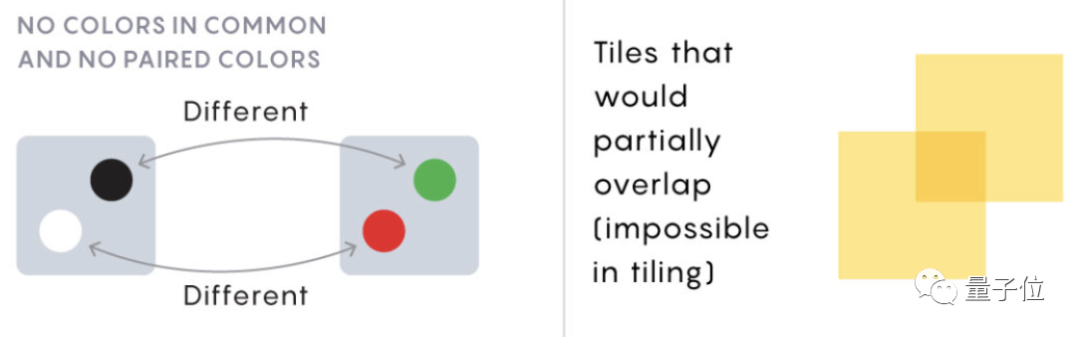
3、一對點顏色相同，另一對點顏色配對，表示兩個正方形共用一個邊

4、一對點顏色不同，另一對點顏色配對，表示兩個正方形的邊相互接觸但不重合

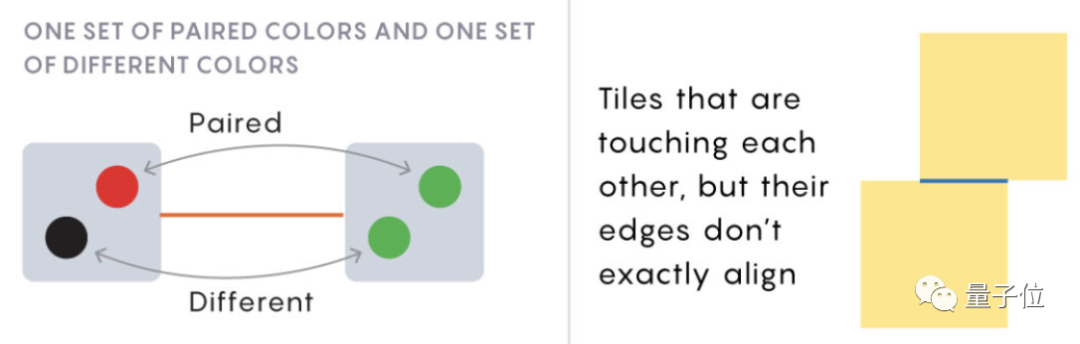
2個點的凱勒圖，要用2對顏色去填充牌面，總共有16種情況。

然后我們把這16張牌擺在桌上，只有符合前面條件4的兩張牌，才用線將二者連起來。這樣就構(gòu)成了一張“凱勒圖”。

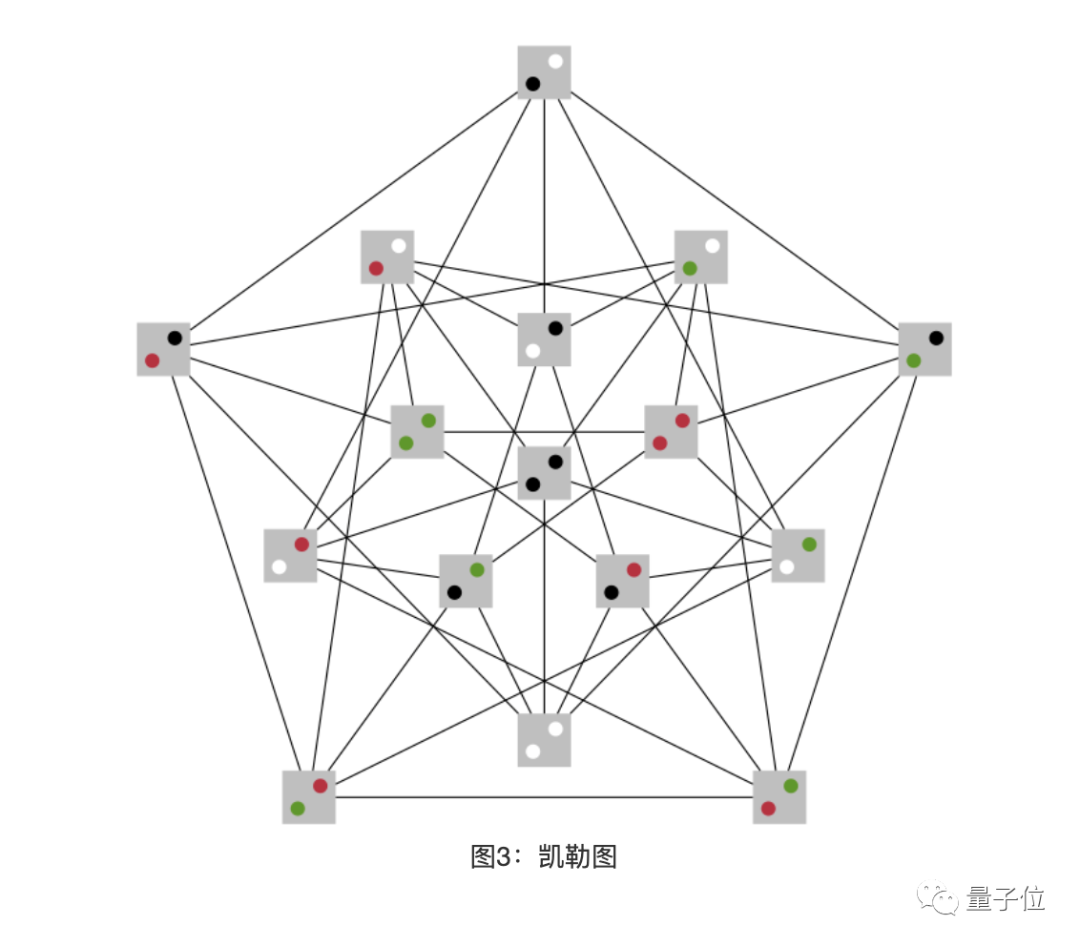
包含16張牌的凱勒圖就描繪了正方形填補平面的所有可能。

如果2維空間中凱勒猜想不成立，那么我們肯定能找到4個正方形，它們之間沒有共用的邊，但是能夠無縫隙填在一起。然后在屏幕上無限復(fù)制這4個正方形，就能填滿整個屏幕。

實際上并不可能。如果按此操作，只會得到有著無數(shù)孔隙（下圖紫色部分）的填充方式。

對應(yīng)到凱勒圖中，就是找在圖中找到4張牌，它們兩兩之間都有連線。（在數(shù)學(xué)里，這叫做完全圖。）

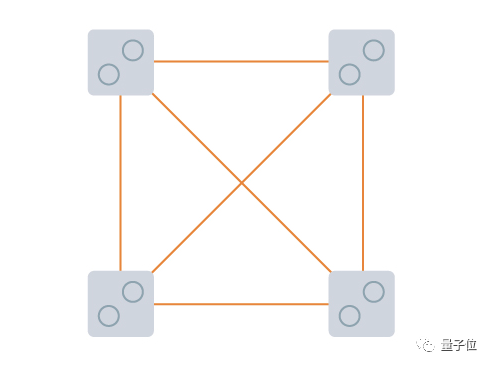
顯然，在2維問題的凱勒圖中，我們找不到這樣的4張牌。（可以自己去上面的凱勒圖中找找看。）

這樣，我們把就把n維立方體以及位移s與牌的點數(shù)n、顏色對數(shù)s聯(lián)系起來。

作為更一般的規(guī)則，如果要證明n維凱勒猜想是錯的，就要在對應(yīng)的凱勒圖中找到2ⁿ張牌，且這些牌兩兩相連。

正因為你找不到4個張牌組成的完全圖，所以2維空間的凱勒猜想是對的。

為了在3維空間中證明凱勒猜想，可以使用216張牌，每張牌上3個點，并可以使用3對顏色（這一點相對靈活）。然后，我們需要尋找2³=8張牌 ，它們兩兩之間都有連線，但還是找不到。

到了8維空間中，我們總算可以找到符合條件的256張牌，所以8維空間的凱勒猜想是錯的。

△8維空間中的一個反例（一個凱勒圖的完全子圖）

接下來的事情就是在7維空間對應(yīng)的凱勒圖上尋找完全子圖。然而這個問題卻從8維問題解決后被擱置了17年。

根據(jù)前面的說明，求解8維空間和10維空間的凱勒猜想，要尋找2⁸=256和2¹⁰=1024張牌的子圖，而7維空間只要尋找2⁷=128張牌的子圖。

后者的難度似乎更小，7維空間的問題應(yīng)該更簡單啊！其實不然。

因為，從某種意義上說，8維和10維可以“分解”為容易計算的較低維度，但7維不行。

證明了10維情況的Lagarias說：“7維不好，因為它是質(zhì)數(shù)，這意味著你無法將其分解為低維。因此別無選擇，只能處理這些圖的全部組合。”

對于人腦來說，尋找大小為128的子圖是一項艱巨的任務(wù)，但這恰恰是計算機擅長回答的問題。

計算機幫忙

說干就干，此前證明8維問題的CMU教授Mackey拉上了斯坦福的數(shù)學(xué)在讀博士Brakensiek和專長計算機輔助證明的助理教授Heule。

回憶起立項的那天，Mackey說，Brakensiek是真正的天才，看著他就像看著NBA總決賽里的詹姆斯。Brakensiek本人確實很厲害，他曾是2013/14兩屆國際信息學(xué)奧賽金牌得主。

△?論文第一作者Brakensiek

言歸正傳。為了方便計算機求解，他們換了個方向來思考：

先設(shè)定牌上有7個點、6種可能的顏色，按照前面的“條件4”對這些牌上色，看看能不能找到128種不同的填色方法。如果找不到，那么凱勒猜想成立。

用計算機輔助證明數(shù)學(xué)問題，還需要把它變成一系列邏輯運算，也就是處理01之間的與或非關(guān)系。

若要求解7維，則總共包含39000個不同布爾變量（0或1），有2³⁹⁰⁰⁰種可能性，這是一個非常非常大的數(shù)字，有11741位數(shù)。

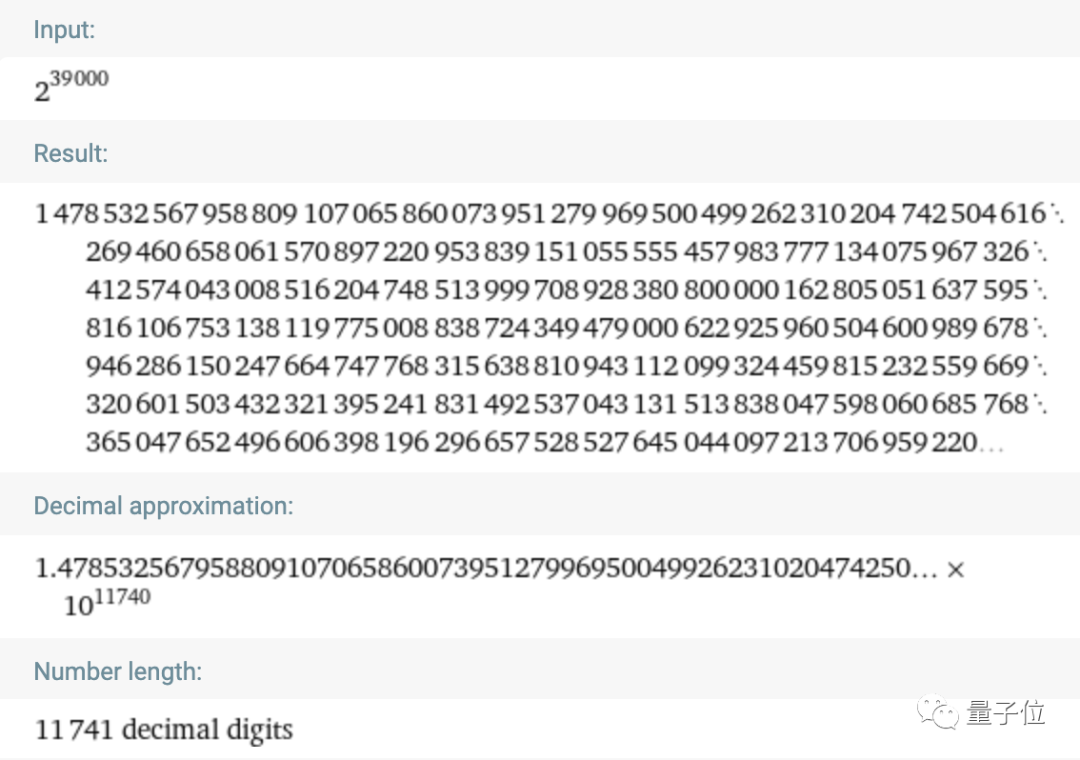
△2的39000次方（來自Wolfram Alpha運算結(jié)果）

一臺普通電腦只能處理324位數(shù)種可能，離解決問題還遠得很。就算交給超級計算機也不夠。

但是，這幾位數(shù)學(xué)家想到了排除法，只要得到結(jié)論，而不必實際檢查所有可能性。效率才是王道！

比如，用計算機規(guī)則給128張牌上色，當你涂到第12張牌的時候，發(fā)現(xiàn)找不到符合條件的下一張牌了。那么所有包含這12張牌的排列都可以排除。

提升效率的另一種方式是利用對稱性。如果已經(jīng)驗證了某種排列不可能，那與之對稱的所有情況都可以排除。

通過這兩種方法，他們把搜索空間縮小到10億（2³⁰）。這樣一來，用計算機搜索變成了可能。

最終，他們僅計算了半個小時，便有了答案。

計算機沒有找到符合條件的128張牌，所以7維空間的凱勒猜想確實成立。

實際上，計算機提供的不僅僅是一個答案，證明的內(nèi)容多達200GB。4位論文作者將證明送入計算機的證明檢查器，確認了它的可靠性。

解決了凱勒猜想后，Heule的下一個目標是用計算機證明數(shù)學(xué)里“最簡單的不可能問題”——3n+1猜想，去年陶哲軒已經(jīng)“幾乎”解決了這個問題，現(xiàn)在可能只差一步之遙了。

參考鏈接：
https://www.quantamagazine.org/computer-search-settles-90-year-old-math-problem-20200819/
https://www.cs.cmu.edu/~mheule/Keller/
https://mathworld.wolfram.com/KellerGraph.html

論文地址：
https://arxiv.org/abs/1910.03740

源代碼：
https://github.com/marijnheule/Keller-encode

以上，便是今天的分享，希望大家喜歡，覺得內(nèi)容不錯的，歡迎點擊「在看」支持，謝謝各位

更多精彩：

中國程序員VS美國程序員，太形象了...
你從未見過的“地獄級”爛項目
為什么Java中1000==1000為false，而100==100為true？

點擊“閱讀原文”，領(lǐng)取 2020 年最新免費技術(shù)資料

↓↓↓?