在分布式算法改進后，算法因為分布式情況，存在通信、等待、同步、異步等問題，導致算法的空間復雜度、時間復雜度，沒有達到預想的情況，針對機器學習的單體算法和分布式算法的優(yōu)化方法，本節(jié)就來介紹相關原理和實現(xiàn)方法

一、單體算法優(yōu)化

針對機器學習的算法模塊，我們需要將它定性成為不同的功能模塊，對算法進行優(yōu)化，并且拆解成為分布式的優(yōu)化方法，本節(jié)先來探討單體算法的優(yōu)化方法。

我們先從簡單的線性規(guī)劃進行處理，線性回歸的目標函數(shù)，如下所示：

如果使用梯度下降法法，每次更新模型，會隨著數(shù)據量和數(shù)據維度，計算量進行線性增加，我們需要采用一些方法，降低它的計算規(guī)模。

1．隨機梯度下降

最常用的單體優(yōu)化算法，是隨機梯度下降算法SGD。它采用對數(shù)據樣本，進行隨機采樣，它的更新公式，如下所示：

它的算法描述，具體如下所示：

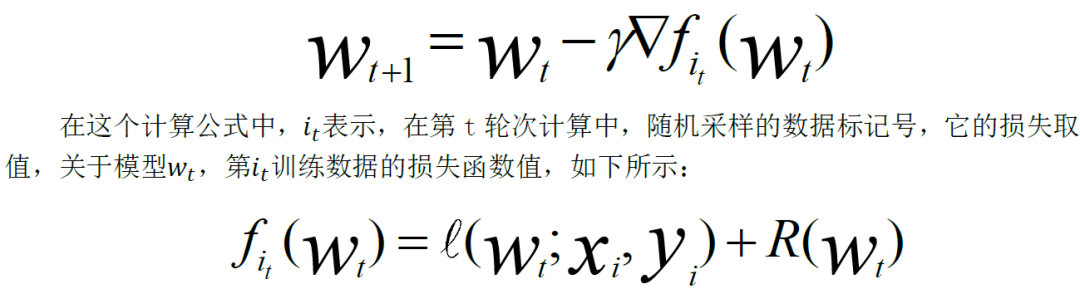
void Stochastic_gradient_descent(){  initialize:初始化w0參數(shù)  Iterate：for t= 0,1,…,T-1 遍歷所有樣本  Selecte:隨機選取樣本  計算：獲得梯度  更新：更新參數(shù)}

對于全局的樣本，都用來計算，會取得數(shù)據損失函數(shù)的平均值，我們采用隨機更新，隨機抽取樣本，可以大大減少計算量，使用隨機梯度作為梯度的自然替代，可以極大提高學習效率。

2．隨機坐標下降

除了隨機梯度的方式，也可以使用隨機坐標下降，對整體算法進行優(yōu)化。它的原理是對模型維度進行隨機采用，從而優(yōu)化算法模型的訓練，它的更新公式，如下所示：

void random_coordinate_descent(){  Initialize: 初始化w0參數(shù)  Iterate：for t= 0,1,…,T-1 遍歷所有樣本  Selecte:隨機選取模型維度  計算：獲得梯度  更新：更新參數(shù)}

3．牛頓法

牛頓法，也是一個高效的優(yōu)化算法，它的核心是使用泰勒展開式，來實現(xiàn)優(yōu)化，它的更新公式，如下所示：

當我們使用一階泰勒站開始，求取零點，計算方法如下所示：

由此，我們可以看出最優(yōu)化求解，最終迭代的形式，歸納方程，如下所示：

求解目標函數(shù)最小值，不斷迭代，沿著函數(shù)下降方向，逐步到達最優(yōu)店，牛頓法，每次迭代步長值，如下所示：

當我們在實際的模型優(yōu)化應用中，可以先對損失函數(shù)，進行一階、二階求導，具體如下所示：

（1）損失函數(shù)，如下所示：

（2）一階求導，如下所示：

（3）二階求導，如下所示：

最終求和公式，轉換為一個矩陣乘法的轉換，參與1和參數(shù)0之間的關系，可以求解如下所示：

其中H就是二階導數(shù)的簡化，它被稱為hessian矩陣，J函數(shù)表示對參數(shù)的一階求導，大寫的X和y表示矩陣，這就是牛頓法應用在最優(yōu)參數(shù)求解的應用。

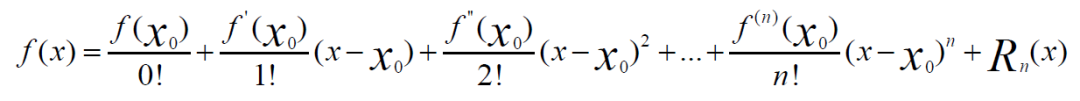
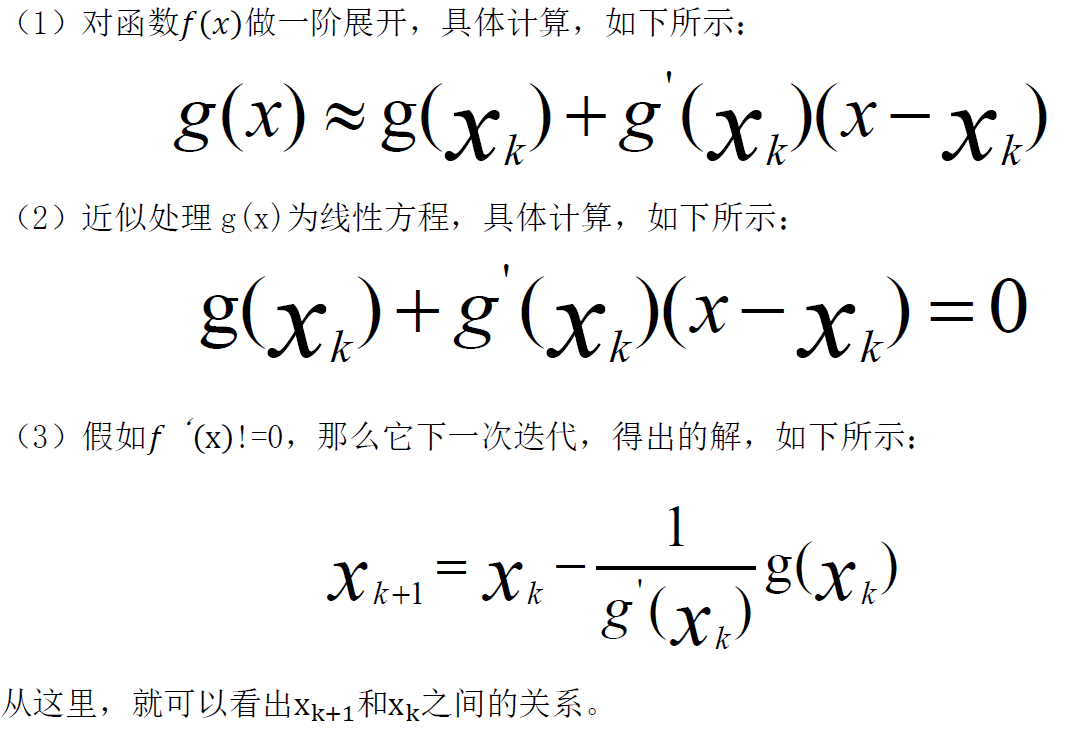
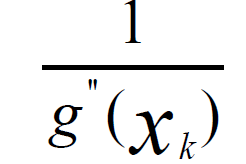
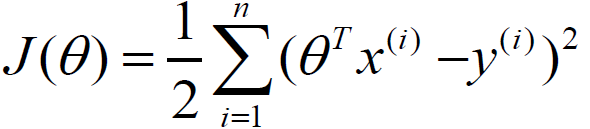
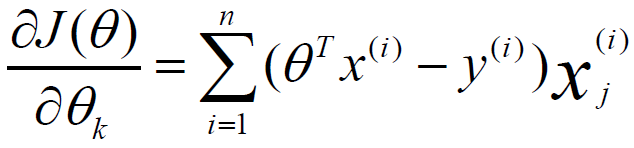
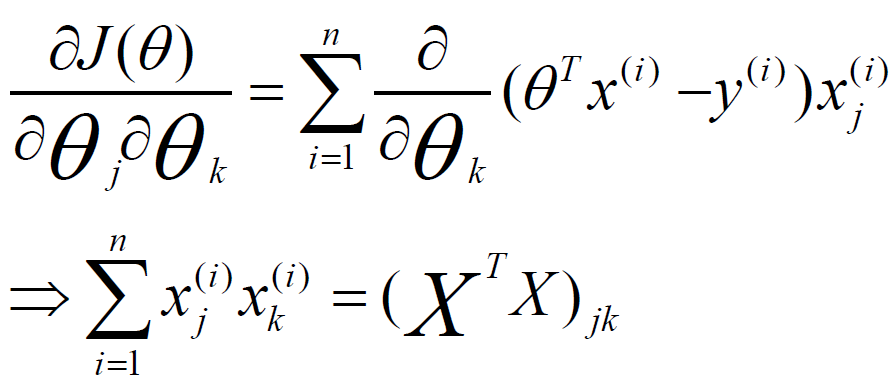
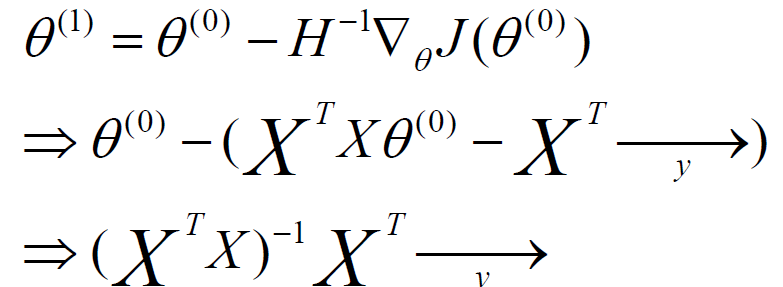
二、分布式異步隨機梯度下降

在本書中，我們介紹了幾個經典的單機優(yōu)化算法，在分布式系統(tǒng)下，我們還可以借助分布式的計算能力，再次提高優(yōu)化效率，本節(jié)應用隨機梯度下降算法為例，講解分布式的算法優(yōu)化方法。

假設我們有一個集群服務器，設置四個計算節(jié)點W1、W2、W3、W4，W1負責迭代兩個模型參數(shù)a、d，W2負責迭代產生參數(shù)b、e，W3負責迭代產生參數(shù)c、f，W4作為最后的計算節(jié)點，產生參數(shù)g，把它們的參數(shù)傳遞順序，以數(shù)字標注傳遞順序。通過BSP協(xié)議，W1、W2、W3先將參數(shù)a、b、c傳遞給參數(shù)服務器，等待W4傳遞參數(shù)g給參數(shù)服務器，參數(shù)服務器根據獲得的數(shù)據，計算平均真實梯度值，獲得最新全局參數(shù)，同步全局參數(shù)到所有工作節(jié)點，計算節(jié)點W1、W2、W3獲得參數(shù)，進入下次迭代，計算得到參數(shù)d、e、f。具體工作流程，如圖1所示：

圖1 ? ?分布式環(huán)境下參數(shù)的同步

在異步更新的情況下，傳遞參數(shù)的順序和上面相同，它不用進行等待，W1、W2、W3傳遞參數(shù)給參數(shù)服務器后，會立即獲得更新后的全局參數(shù)，進入下次迭代，這樣會導致產生多個全局參數(shù)的版本。在異步環(huán)境下，使用梯度值對全局進行更新，對于算法的收斂影響比較大，如圖2所示，是異步參數(shù)的更新情況：

圖2 ?參數(shù)異步更新和變化

針對異步更新，殘生多個全局參數(shù)，算法收斂的問題，我們可以進行如下處理：

（1）在計算節(jié)點上，分別計算梯度值，不直接發(fā)送給參數(shù)服務器，使用梯度值，計算本地權重參數(shù)。

（2）發(fā)送權重參數(shù)給參數(shù)服務器，參數(shù)服務器接收本地參數(shù)后，使用本地參數(shù)，更新全局參數(shù)。

（3）使用Wt表示當前參數(shù)服務器的全局參數(shù)，Wct表示計算節(jié)點傳的參數(shù)值，Wt+1表示計算后的新全局參數(shù)，再引入變量α，表示本地參數(shù)在全局權重，最終它的計算公式如下所示：

在工作節(jié)點更新是，不完全參數(shù)服務器上的參數(shù)，每個計算節(jié)點，智能代表它這個節(jié)點的結果，全局更新時候，需要根據所有工作節(jié)點的參數(shù)值和權重，進行根性，這里可以使用線性插值法，具體計算如下所示：

（1）計算新的本地權值參數(shù)

（2）參數(shù)服務器，接收到某個計算節(jié)點的參數(shù)，更新它的參數(shù)公式，如下所示：

（3）合并上述兩步，最終得到參數(shù)服務器參數(shù)，根據某個計算節(jié)點的權值參數(shù)，修正全局參數(shù)的公式，如下所示：

如果計算節(jié)點只有一個，和同步SGD算法的公式，也保持了一致。

算法的實現(xiàn)偽代碼，如下所示：

客戶端算法

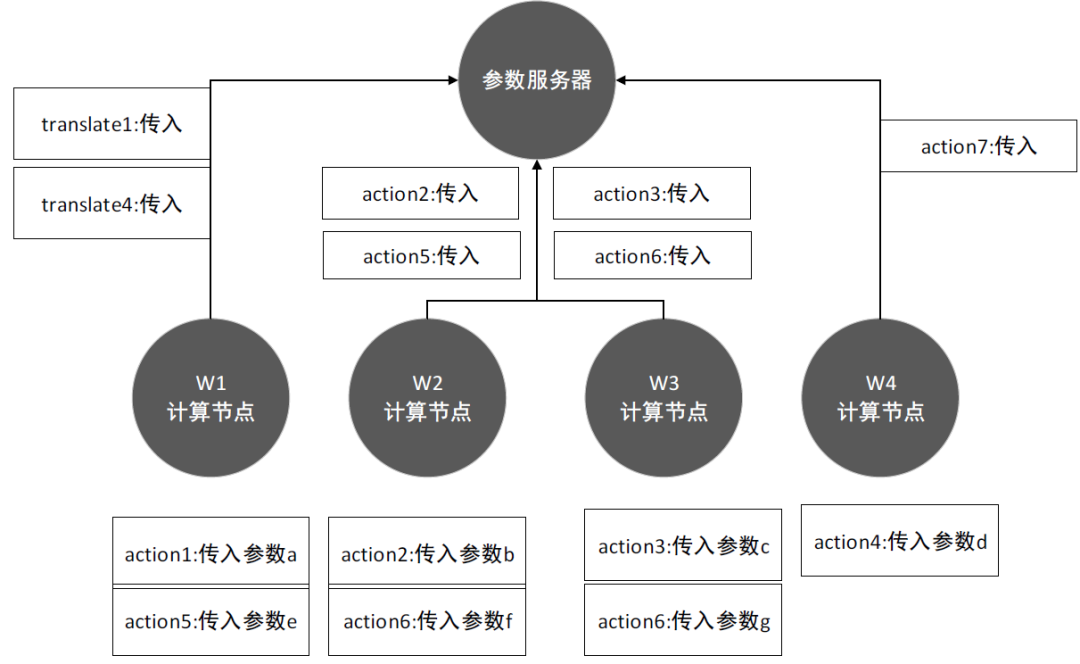
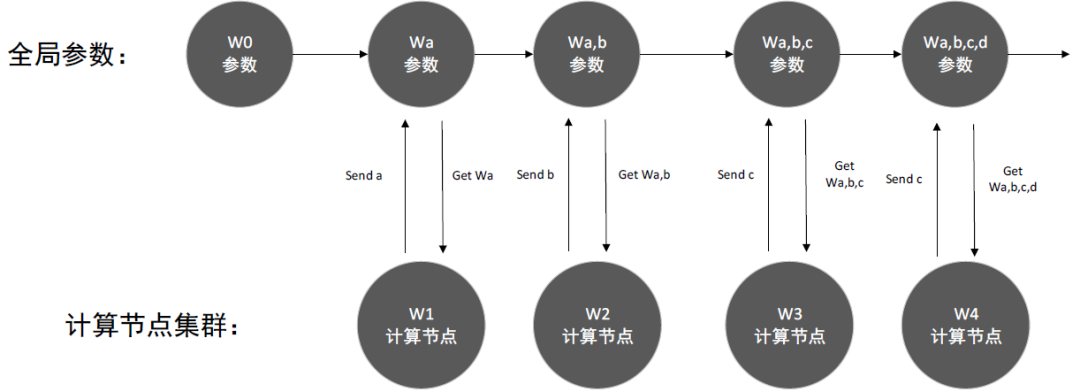
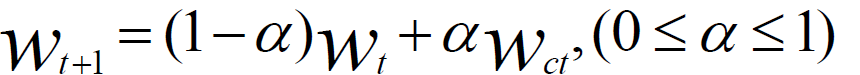
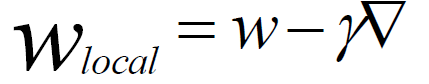
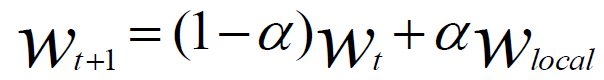
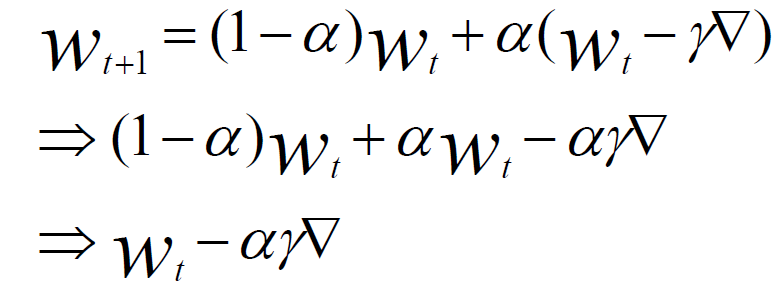
void SGD_Client(){  ProcedureWork(Parameterw,Mini-batch-sizeNc    Initialize:total gradientg = 0    For all i∈{1...Nc} do      g←g + ComputeGradient(data,w)    End For    Server.Update(c,g)    stepc ←stepc +1}

參數(shù)服務器算法

void SGD_Server(){  Procedure DispatchJob(Client c,Parameter wt)    Call procedure Work(wt,Nc)for client c  End  Procedure Update(Client c,Gradient g)    wt+1 ←wt ? AdaGrad(g)    t←t+1    If c is the last client whose stepc =the server step then      step←step+1    End If    If running then      DispatchJob(c,wt)    End If  End}

整體的運行工作流程，如圖3所示：

圖3 ?分布式異步SGD算法運行流程示意

以上我們就完成了隨機梯度下降算法，在分布式異步環(huán)境的算法改進，關于其他的算法改進，讀者可以參考上述原理，自行研究改進方法，適應應用環(huán)境。

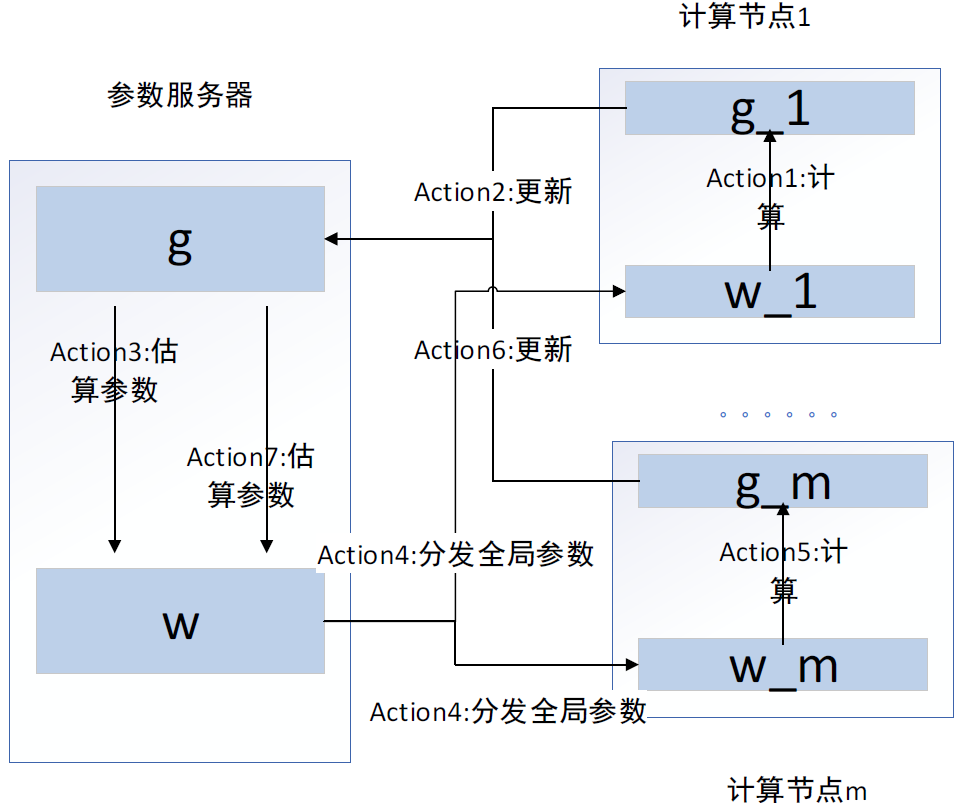
本書摘自機械工業(yè)出版社---《分布式人工智能：基于TensorFlow RTOS與群體智能體系》一書，經授權刊登此公號。

《分布式人工智能基于TensorFlow、RTOS與群體智能體系》結合分布式計算、大數(shù)據、機器學習、深度學習和強化學習等技術，以群體智能為主線，講述分布式人工智能的原理與應用。本書首先介紹分布式系統(tǒng)的概念、技術概況、計算框架、智能核心及體系架構等內容；然后介紹大數(shù)據框架、高速計算、海量存儲及人工智能經典算法等內容；接著介紹大規(guī)模分布式系統(tǒng)架構與演進，以及群體智能與博弈等內容；最后搭建《星際爭霸2》仿真環(huán)境，并開發(fā)相關的仿真對抗系統(tǒng)。

如果你對以上內容感興趣

快在留言區(qū)大聲告訴我們

截止2月1日晚八點

留言獲贊數(shù)最高的五位同學各贈一本

《分布式人工智能基于TensorFlow、RTOS與群體智能體系》

沒有抽中的粉絲不要氣餒，可在當當網購買此書，快快來搶購吧。

上述內容，如有侵犯版權，請聯(lián)系作者，會自行刪文。

送書了！分布式人工智能算法詳解

一、單體算法優(yōu)化

二、分布式異步隨機梯度下降

本書摘自機械工業(yè)出版社---《分布式人工智能：基于TensorFlow RTOS與群體智能體系》一書，經授權刊登此公號。