淺析傅里葉變換
原文鏈接:https://github.com/Jezzamonn/fourier
譯者:virtualwiz
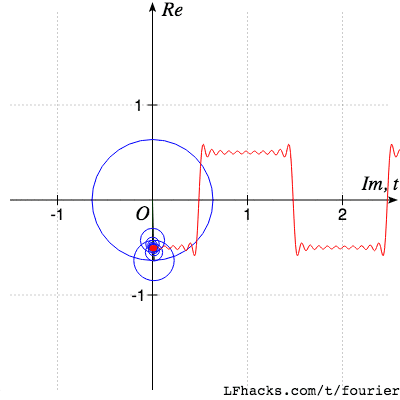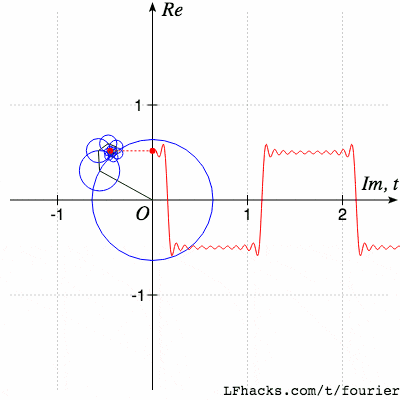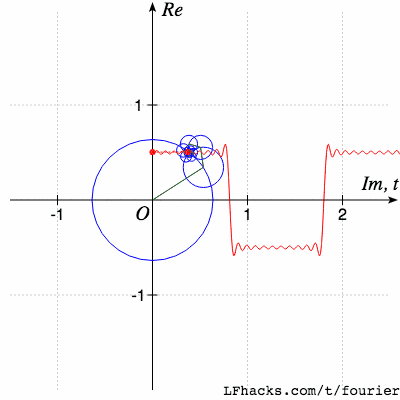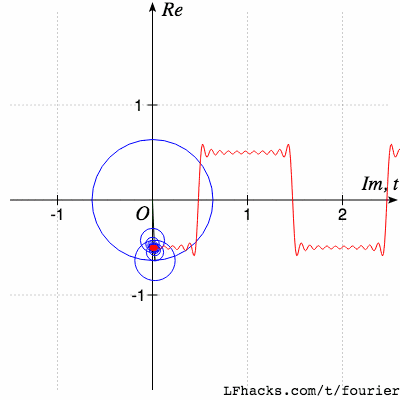
傅里葉變換是一種在各個領域都經(jīng)常使用的數(shù)學工具。這個網(wǎng)站將為你介紹傅里葉變換能干什么,為什么傅里葉變換非常有用,以及你如何利用傅里葉變換干漂亮的事。就像下面這樣:
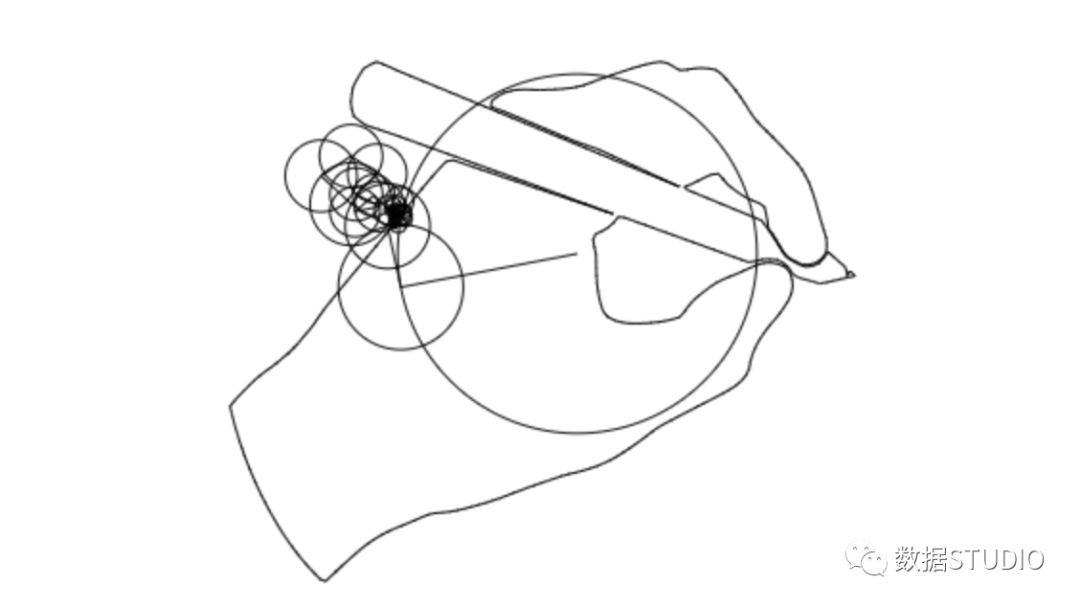
我將為你解釋這個動畫是如何工作的,沿途為你詳細地解釋傅里葉變換!
這次旅途結束后,你將會掌握下面這些知識:
什么是傅里葉變換 傅里葉變換的一些實際用途 傅立葉變換的一些很酷的用法(雖然有些沒有實際意義)
我們現(xiàn)在暫時不提那些復雜的數(shù)學公式。傅里葉背后的數(shù)學原理十分有趣,但最好還是先從它的實際應用開始,以及為什么要使用它。如果你想了解更多,下面提供了一些進一步的閱讀建議!
傅里葉變換是什么
簡而言之,傅里葉變換把一個輸入信號分解成一堆正弦波的疊加。就像大多數(shù)數(shù)學方法一樣,這個名字來自一個名叫傅立葉的人。
讓我們從一些簡單的例子開始,然后繼續(xù)前進。首先,我們來看看什么是波 —— 波隨著時間的推移,一直按照某一規(guī)律變化。
這是一個波的例子:
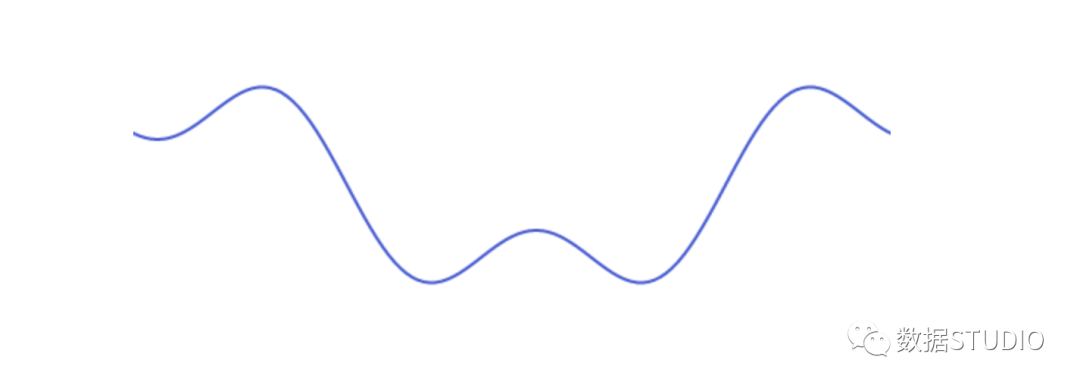
這個波可以分解為兩個正弦波的疊加。也就是說,當我們將兩個正弦波相加時,就會得到原來的波。
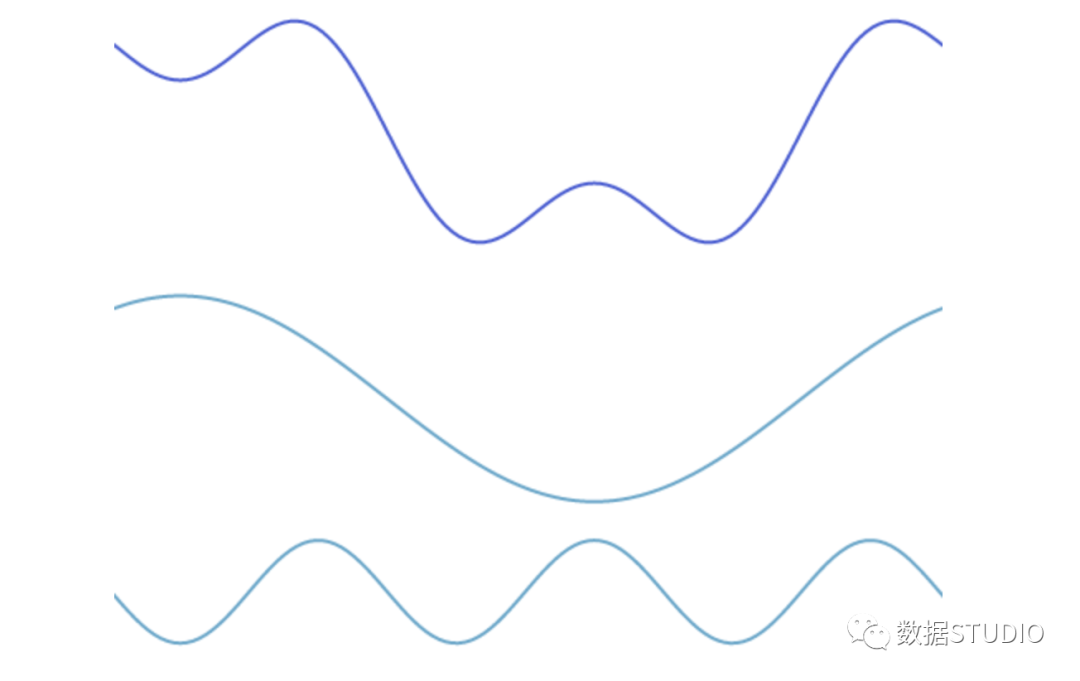
傅里葉變換可以讓我們從一個復雜的波形里面,把構成這個波的單個正弦波分離出來。在這個例子中,你幾乎可以通過“腦補”完成這一操作。
為什么?事實證明,現(xiàn)實世界中的許多事物間的互相交互,都是基于正弦波。我們通常將這種波的快慢的性質(zhì),稱為波的頻率。
最明顯的例子就是聲音 —— 當我們聽到聲音時,我們聽不到那條波浪線,但我們聽到構成聲音的正弦波的不同頻率。
能夠在計算機上區(qū)分這兩個音調(diào),我們就可以了解一個人實際可以聽到的內(nèi)容。我們可以理解聲音的高低,或弄清楚這個波包含了什么音符。
一些波看起來不像由正弦波構成,我們也可以用這個分解的過程來進行分析。
我們來看看這個家伙吧。這個波稱為方波。

雖然看起來不太可能,但它確實也可以分解成正弦波。
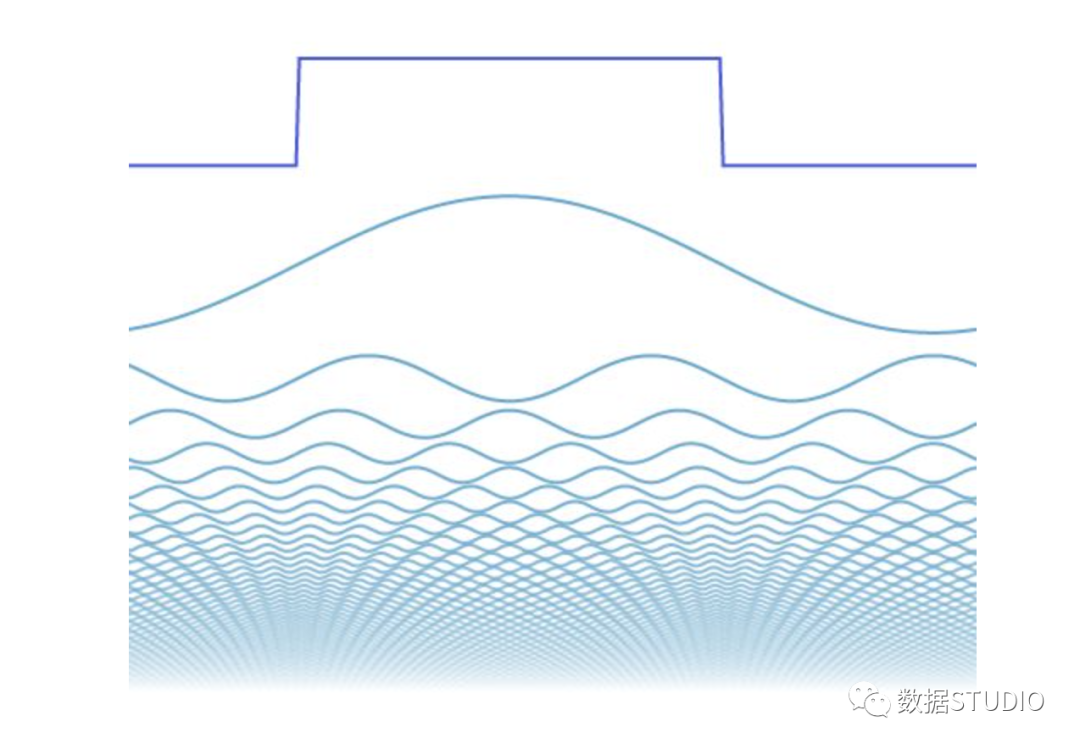
這次我們需要很多 —— 理論上是無限多的正弦波來完美地表達一個方波。隨著我們加入越來越多的正弦波,疊加出的波形就越來越接近方波。
在視覺上,你會注意到前幾個正弦波的疊加可以在結果中產(chǎn)生最大差異。滑塊滑到一半時,就有一些方波的樣子了,但它看起來搖擺不定。加上更多小的正弦波,組合出的波形看起來就平坦了。
當播放這個波形時,你會發(fā)現(xiàn)使用的正弦波少時,聲音聽起來更低沉一些。這是因為我們把高頻率的成分去掉了。
這一過程可以用來處理任何有周期的波。試一試,畫一個你喜歡的波形吧。
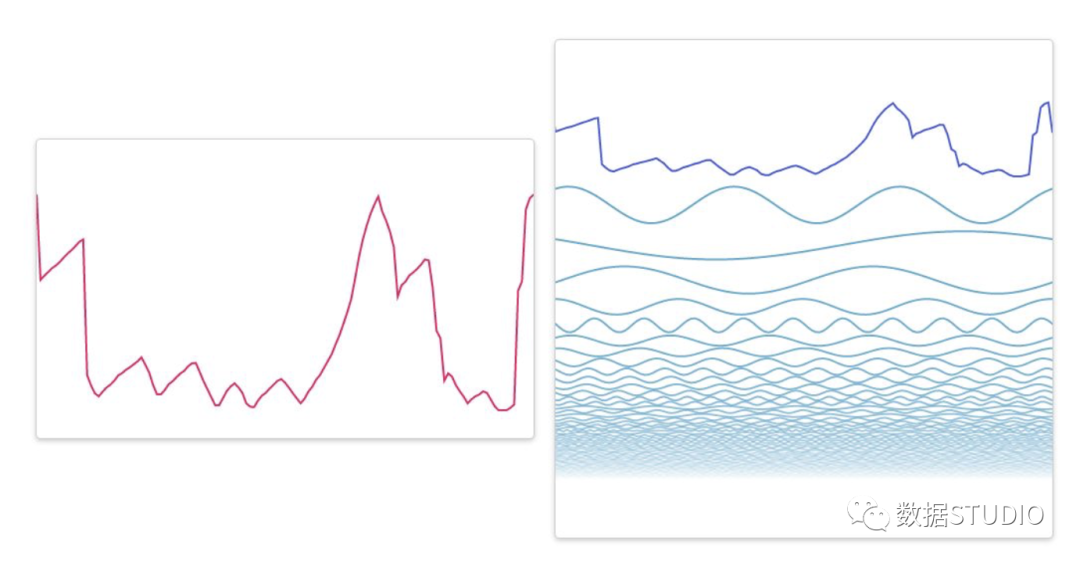
隨便畫一個波形都能用多個正弦波表示
移動滑塊來觀察,正弦波加得越多,組合出的波形越接近你畫的原始波形。
和上一個方波類似,除了有些額外的擺動之外,滑塊移動到中間位置,生成的波形就很接近你畫的了。
我們可以利用這個事實:使用傅里葉變換,我們可以把音頻中最重要的成分表達出來,并且得到和原始聲音非常接近的波形。
在計算機中,波形以一系列數(shù)據(jù)點的形式來存儲。
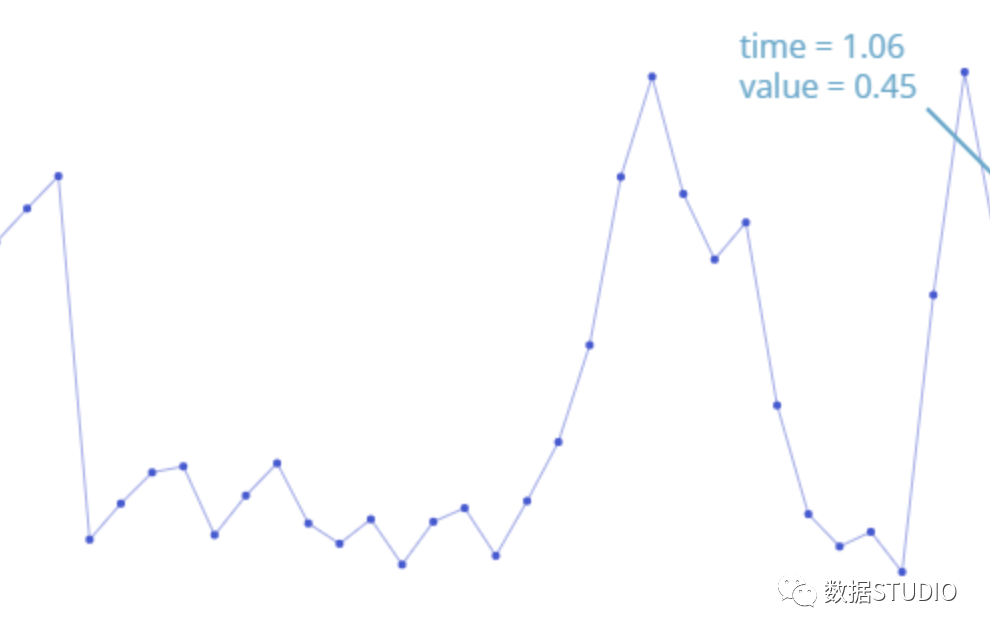
我們可以做的是,將聲音表示為一堆正弦波。然后可以通過忽略掉較小幅度的高頻成分來壓縮聲音。盡管得出的波形與原始波形不一樣,但是聽起來將會和原始聲音很接近。
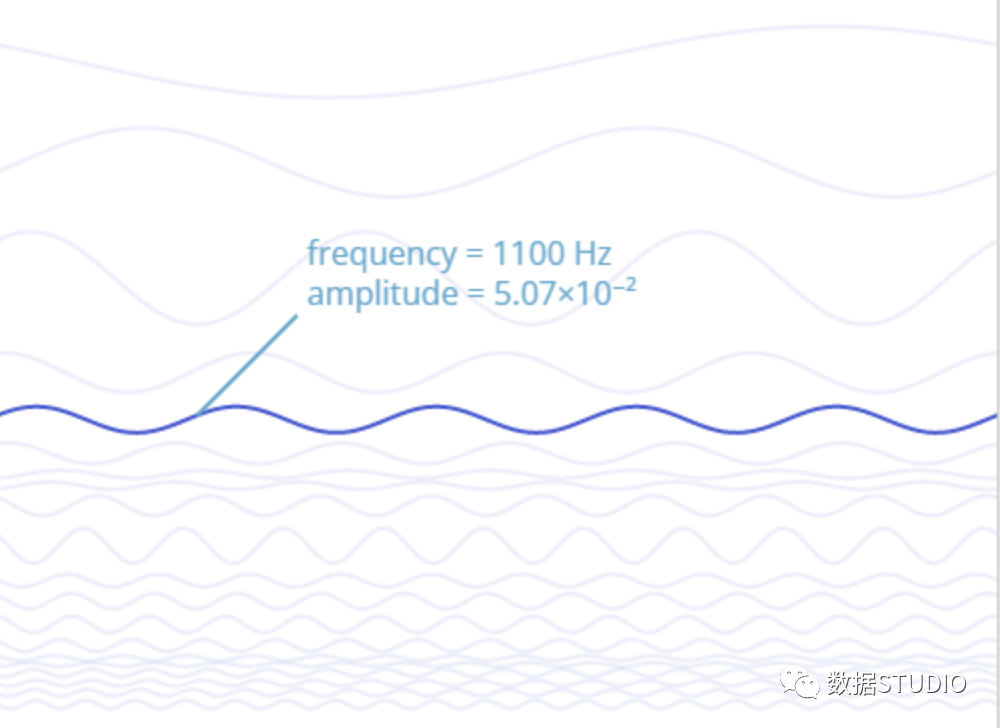
這基本上就是MP3做的事情。MP3除此之外還可以更聰明地知道需要保留哪些頻率以及扔掉哪些頻率。
所以在這種情況下,我們可以使用傅里葉變換來理解波的基本屬性,然后我們可以將它用于數(shù)據(jù)的壓縮之類的事情。
好的,現(xiàn)在讓我們深入了解傅立葉變換。下一部分看起來很酷,也讓你更加了解傅立葉變換的作用。但大多只是“看起來”很酷。
周轉圓
在開始時,我介紹了傅里葉變換可以將事物分成正弦波。但更酷的是,它產(chǎn)生的正弦波不僅僅是一般的正弦波,它們都是“三維”的正弦波。你可以稱之為“復雜的”正弦曲線,或者,“螺旋”。

如果我們從側面看,它們看起來像正弦波。但是,從正面看,它們看起來像圓圈。
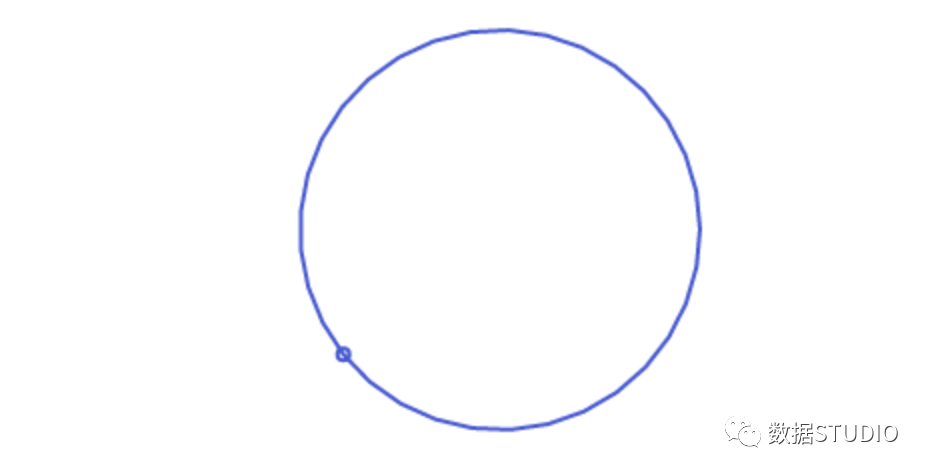
到目前為止,我們所做的一切只需要常規(guī)的2D正弦波。當我們對2D波進行傅里葉變換時,“復雜的”部分被忽略了,所以我們最終也只能得到正弦波。
但是我們可以使用3D正弦波來制作看起來很有趣的東西,就像這個:
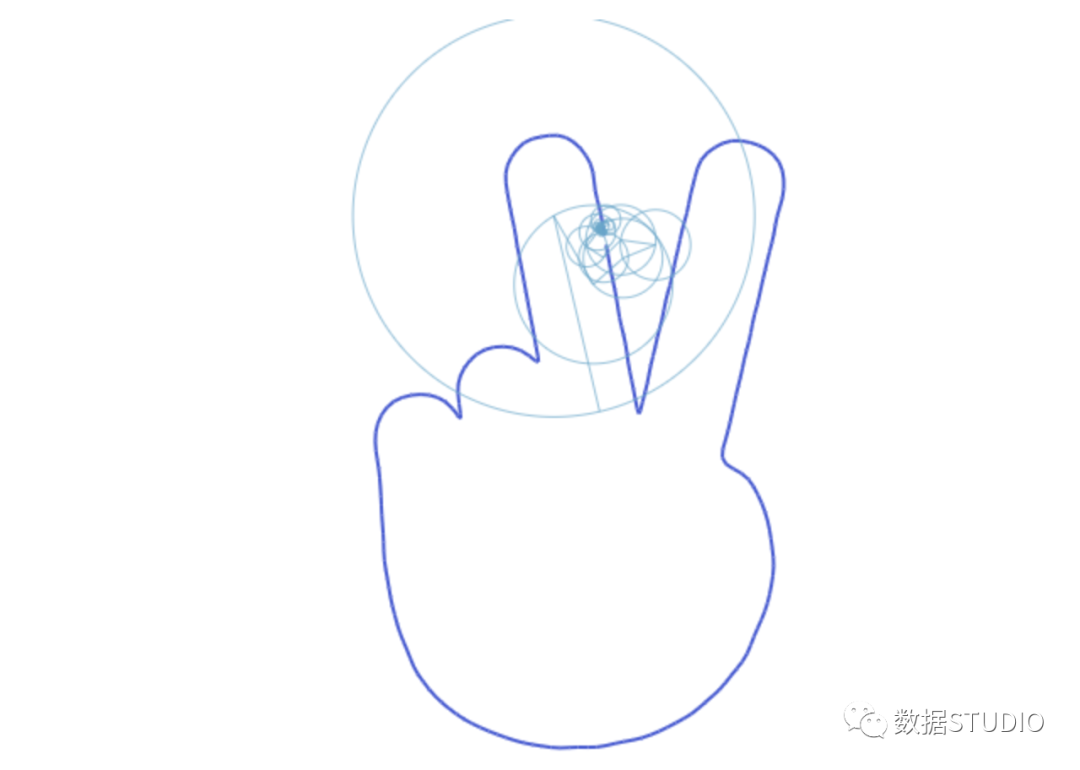
這里發(fā)生了什么事情呢?
我們可以將一個手繪圖理解為一個3D的形狀,因為點的位置在隨時間移動。如果你想象一個人正在繪制一只手,那么這三個維度就代表了某一時刻鉛筆尖的位置。除了x和y維度告訴我們筆尖的位置,還有一個時間維度。

現(xiàn)在我們有一個3D的形狀,我們不能使用常規(guī)2D正弦波把它表示出來。無論我們添加多少2D正弦波,我們都永遠不會得到3D。所以我們需要些別的東西。
我們可以使用的是之前的3D螺旋正弦波。如果我們添加很多這些螺旋,得到的東西就看起來像我們的3D形狀。
請記住,當我們從前面看它們時,這些波浪看起來像圓圈。圍繞另一個圓圈移動的圓圈圖案,被稱為“周轉圓”。
像以前一樣,我們只用幾個圓圈就可以很好地近似表達出原始圖案。因為這是一個相當簡單的形狀,所有后面添加的小圓都是使邊緣更加銳利。
這些適用于任何一個圖案。真的,現(xiàn)在你創(chuàng)作的機會來了。

同樣,你會發(fā)現(xiàn),對于大多數(shù)形狀,我們可以用很少的圓圈很好地近似表達它們,要保存一個形狀,我們不必保存形狀上所有的點。
這個方法可以應用于實際數(shù)據(jù)嗎?答案是可以!實際上,我們有另一種稱為SVG的數(shù)據(jù)格式,比我們在這里繪制圖案更好用一些。所以目前,我們只是制作了些炫酷的小GIF。
然而,還有另一種類型的視覺數(shù)據(jù)使用傅里葉變換。
JPEGs
你知道傅立葉變換除了可以表達簡單的手繪線條,還可以用于圖像嗎?事實上,我們一直都在使用它,因為這就是JPEG的工作原理!我們將相同的原理應用于圖像 —— 將某些東西分成一堆正弦波,然后只存儲重要的東西。
要處理圖像,我們需要一種不同類型的正弦波。我們需要這樣的一種“正弦波”:無論我們有什么樣的圖像,我們都可以添加一堆這些正弦波來回到原始圖像。
要做到這一點,我們使用的每個正弦波也將是一個個小圖像。我們現(xiàn)在使用一些黑白條紋的小圖像,這些更可以表達為“線”,而不是波。為了表示“波”的大小,每個圖像將具有或多或少的明暗對比。
我們也可以以類似的方式表示出顏色,但我們先從灰度圖像開始玩。為了表示灰度圖像,我們需要一些水平的波圖案,

還有一些垂直的波圖案。

就其本身而言,只有水平和垂直圖像還不足以表達出我們可以看到的圖像。我們還需要一些額外的圖案,將兩者相乘。

要得到一個8x8分辨率的圖像,這里是我們需要的所有小圖案。

如果我們把這些小圖案的對比度調(diào)整到適當?shù)闹担缓髮⑺鼈兿嗉樱覀兙涂梢缘贸鋈我鈭D像。
讓我們從一個字母"A"開始。它非常小,但我們需要它很小,否則我們最終會得到太多其他的圖像。

隨著我們添加越來越多的這些圖案,我們最終得到的東西越來越接近實際圖像。我覺得你只要添加很少一部分圖案,就能看出字母“A”的樣子來。

對于實際的JPEG圖像來說,這就是基本原理,剩下的只有一些額外的細節(jié)。
圖像被分解為8x8塊,每個塊分別進行分解。我們使用一組頻率來確定每個像素的亮度或暗度,然后是另外兩組用于顏色,一組用于紅綠色,另一組用于藍黃色。我們?yōu)槊總€塊使用的頻率個數(shù)決定了JPEG圖像的品質(zhì)。
這是一個實際的JPEG圖像,放大后我們可以看到細節(jié)。當我們改變JPEG品質(zhì)水平時,可以觀察出畫質(zhì)的區(qū)別。


總結
讓我們回顧一下:
傅里葉變換讓我們輸入一個事物,并將其分解為不同頻率的成分 頻率告訴我們有關數(shù)據(jù)的一些基本屬性 并且可以通過僅存儲重要的成分來壓縮數(shù)據(jù) 我們還可以用傅里葉變換的原理,通過一堆圓圈制作看起來很酷的動畫
這只是表面上的一些淺層次應用。傅里葉變換是一個非常強大的工具,因為將事物分解成不同頻率是十分重要的分析方法。它們被用于許多領域,包括電路設計,移動網(wǎng)絡信號,磁共振成像(MRI)和量子物理!
本文內(nèi)容來源以上網(wǎng)址及公眾號。以上內(nèi)容僅供學習使用,不作其它用途,如有侵權,請留言聯(lián)系,作刪除處理!
有任何疑問及建議,掃描以下公眾號二維碼添加交流:
