手把手教你用Python進(jìn)行時(shí)間序列分解和預(yù)測

預(yù)測是一件復(fù)雜的事情，在這方面做得好的企業(yè)會(huì)在同行業(yè)中出類拔萃。時(shí)間序列預(yù)測的需求不僅存在于各類業(yè)務(wù)場景當(dāng)中，而且通常需要對未來幾年甚至幾分鐘之后的時(shí)間序列進(jìn)行預(yù)測。如果你正要著手進(jìn)行時(shí)間序列預(yù)測，那么本文將帶你快速掌握一些必不可少的概念。

目錄

01 什么是時(shí)間序列？

顧名思義，時(shí)間序列是按照固定時(shí)間間隔記錄的數(shù)據(jù)集。換句話說，以時(shí)間為索引的一組數(shù)據(jù)是一個(gè)時(shí)間序列。請注意，此處的固定時(shí)間間隔（例如每小時(shí)，每天，每周，每月，每季度）是至關(guān)重要的，意味著時(shí)間單位不應(yīng)改變。別把它與序列中的缺失值混為一談。我們有相應(yīng)的方法來填充時(shí)間序列中的缺失值。

在開始使用時(shí)間序列數(shù)據(jù)預(yù)測未來值之前，思考一下我們需要提前多久給出預(yù)測是尤其重要的。你是否應(yīng)該提前一天，一周，六個(gè)月或十年來預(yù)測（我們用“界限”來表述這個(gè)技術(shù)術(shù)語）？需要進(jìn)行預(yù)測的頻率是什么？在開始預(yù)測未來值的詳細(xì)工作之前，與將要使用你的預(yù)測結(jié)果的人談一談也不失為一個(gè)好主意。

02 如何在Python中繪制時(shí)間序列數(shù)據(jù)？

可視化時(shí)間序列數(shù)據(jù)是數(shù)據(jù)科學(xué)家了解數(shù)據(jù)模式，時(shí)變性，異常值，離群值以及查看不同變量之間的關(guān)系所要做的第一件事。從繪圖查看中獲得的分析和見解不僅將有助于建立更好的預(yù)測，而且還將引導(dǎo)我們找到最合適的建模方法。這里我們將首先繪制折線圖。折線圖也許是時(shí)間序列數(shù)據(jù)可視化最通用的工具。

這里我們用到的是AirPassengers數(shù)據(jù)集。該數(shù)據(jù)集是從1949年到1960年之間的每月航空旅客人數(shù)的集合。下面是一個(gè)示例數(shù)據(jù)，以便你對數(shù)據(jù)信息有個(gè)大概了解。

#Reading?Time?Series?Data
Airpassenger?=?pd.read_csv("AirPassengers.csv")
Airpassenger.head(3)

現(xiàn)在，我們使用折線圖繪制數(shù)據(jù)。在下面的示例中，我們使用set_index（）將date列轉(zhuǎn)換為索引。這樣就會(huì)自動(dòng)在x軸上顯示時(shí)間。接下來，我們使用rcParams設(shè)置圖形大小，最后使用plot（）函數(shù)繪制圖表。

Airpassenger?=?Airpassenger.set_index('date')
pyplot.rcParams["figure.figsize"]?=?(12,6)
Airpassenger.plot()
pyplot.show()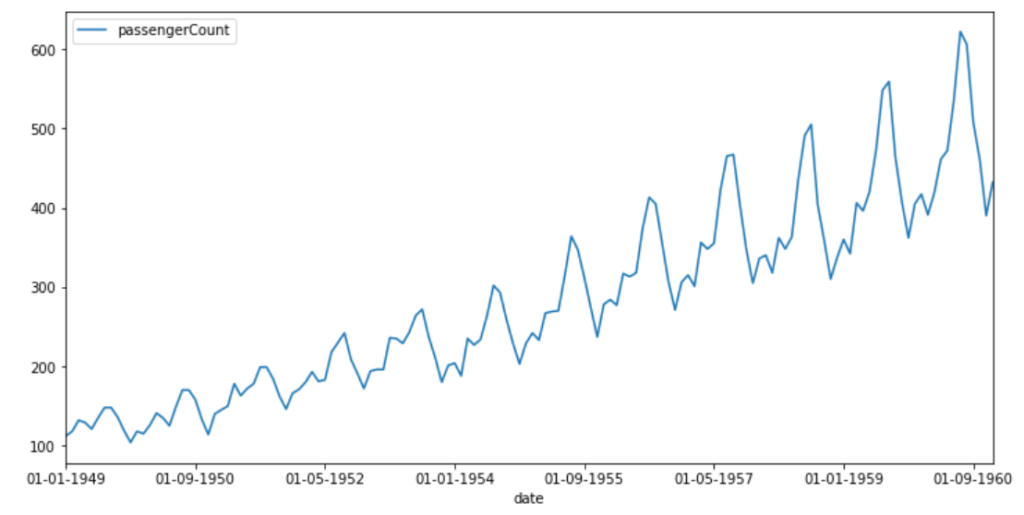

▲航空旅客人數(shù)

1949-1960年間，乘飛機(jī)旅行的乘客人數(shù)穩(wěn)定增長。規(guī)律性間隔的峰值表明增長似乎在有規(guī)律的時(shí)間間隔內(nèi)重復(fù)。

讓我們看看每個(gè)季度的趨勢是怎樣的。為了便于理解，從不同的維度觀察信息是個(gè)好主意。為此，我們需要使用Python中的datetime包從date變量中得出季度和年份。在進(jìn)行繪圖之前，我們將連接年份和季度信息，以了解旅客數(shù)量在季節(jié)維度上如何變化。

from?datetime?import?datetime
#?Airpassenger["date"]?=?Airpassenger["date"].apply(lambda?x:?datetime.strptime(x,?"%d-%m-%Y"))
Airpassenger["year"]?=?Airpassenger["date"].apply(lambda?x:?x.year)
Airpassenger["qtr"]?=?Airpassenger["date"].apply(lambda?x:?x.quarter)
Airpassenger["yearQtr"]=Airpassenger['year'].astype(str)+'_'+Airpassenger['qtr'].astype(str)
airPassengerByQtr=Airpassenger[["passengerCount",?"yearQtr"]].groupby(["yearQtr"]).sum()

準(zhǔn)備好繪制數(shù)據(jù)后，我們繪制折線圖，并確保將所有時(shí)間標(biāo)簽都放到x軸。x軸的標(biāo)簽數(shù)量非常多，因此我們決定將標(biāo)簽旋轉(zhuǎn)呈現(xiàn)。

pyplot.rcParams["figure.figsize"]?=?(14,6)
pyplot.plot(airPassengerByQtr)
pyplot.xticks(airPassengerByQtr.index,?rotation='vertical')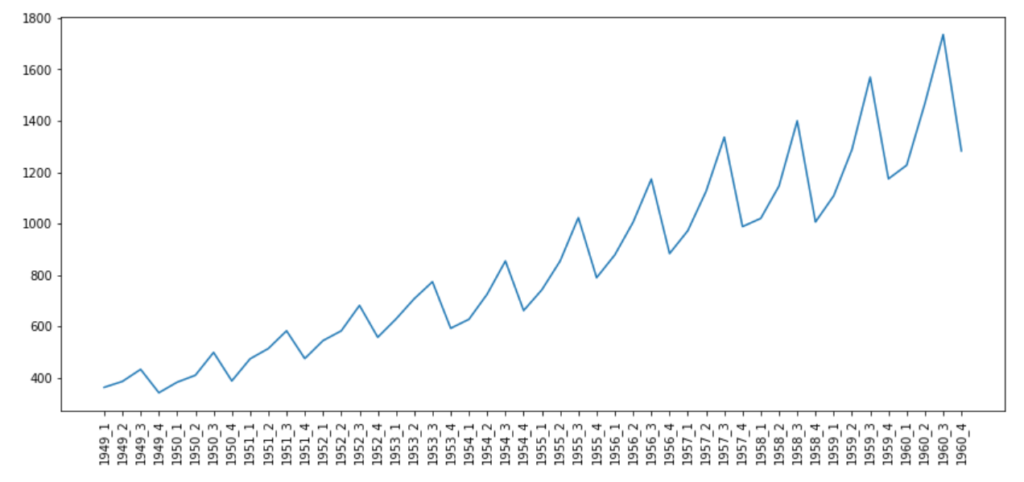

▲每季度的旅客總數(shù)

這幅圖非常有趣，它清晰地表明，在1949-1960年之間的所有年份中，航空旅客人數(shù)每季度都在顯著增加。

03 時(shí)間序列的要素是什么？

時(shí)間序列數(shù)據(jù)包含4個(gè)主要元素：

1. 趨勢性

趨勢性表示數(shù)據(jù)隨時(shí)間增加或減少的一般趨勢。這很容易理解。例如，1949年至1960年之間航空旅客數(shù)量呈增加趨勢，或者可以說呈上升趨勢。

2. 季節(jié)性

如同一年四季，數(shù)據(jù)模式出現(xiàn)在有規(guī)律的間隔之后，代表了時(shí)間序列的季節(jié)性組成部分。它們在特定的時(shí)間間隔（例如日，周，月，年等）之后重復(fù)。

有時(shí)我們很容易弄清楚季節(jié)性，有時(shí)則未必。通常，我們可以繪制圖表并直觀檢驗(yàn)季節(jié)性元素的存在。但是有時(shí)，我們可能不得不依靠統(tǒng)計(jì)方法來檢驗(yàn)季節(jié)性。

3. 周期性

可被視為類似季節(jié)性，但唯一的區(qū)別是周期性不會(huì)定期出現(xiàn)。這個(gè)屬性使得它很難被辨識(shí)。例如，地震可以在我們知道將要發(fā)生的任何時(shí)間發(fā)生，但是我們其實(shí)不知道何時(shí)何地發(fā)生。

4. 隨機(jī)噪聲

不屬于上述三類情況的時(shí)間序列數(shù)據(jù)中的突然變化，而且也很難被解釋，因此被稱為隨機(jī)波動(dòng)或隨機(jī)噪聲。

04 如何分解時(shí)間序列？

有兩種技術(shù)可以獲取時(shí)間序列要素。在進(jìn)行深入研究和查看相關(guān)Python抽取函數(shù)之前，必須了解以下兩點(diǎn)：

那么什么是可加和可乘時(shí)間序列模型呢？

可加性模型–在可加性模型中，要素之間是累加的關(guān)系。

y（t）=季節(jié)+趨勢+周期+噪音

可乘性模型–在可乘性模型中，要素之間是相乘的關(guān)系。

y（t）=季節(jié)*趨勢*周期*噪音

你想知道為什么我們還要分解時(shí)間序列嗎？你看，分解背后的目的之一是估計(jì)季節(jié)性影響并提供經(jīng)過季節(jié)性調(diào)整的值。去除季節(jié)性的值就可以輕松查看趨勢。

例如，在美國，由于農(nóng)業(yè)領(lǐng)域需求的增加，夏季的失業(yè)率有所下降。從經(jīng)濟(jì)學(xué)角度來講，這也意味著6月份的失業(yè)率與5月份相比有所下降。現(xiàn)在，如果你已經(jīng)知道了邏輯，這并不代表真實(shí)的情況，我們必須調(diào)整這一事實(shí)，即6月份的失業(yè)率始終低于5月份。

這里的挑戰(zhàn)在于，在現(xiàn)實(shí)世界中，時(shí)間序列可能是可加性和可乘性的組合。這意味著我們可能并不總是能夠?qū)r(shí)間序列完全分解為可加的或可乘的。

現(xiàn)在你已經(jīng)了解了不同的模型，下面讓我們研究一些提取時(shí)間序列要素的常用方法。

05 經(jīng)典分解法

該方法起源于1920年，是諸多方法的鼻祖。經(jīng)典分解法有兩種形式：加法和乘法。Python中的statsmodels庫中的函數(shù)season_decompose（）提供了經(jīng)典分解法的實(shí)現(xiàn)。在經(jīng)典分解法中，需要你指出時(shí)間序列是可加的還是可乘的。你可以了解有關(guān)加法和乘法分解的更多信息：

https://otexts.com/fpp2/classical-decomposition.html

在下面的代碼中，要獲得時(shí)間序列的分解，只需賦值model=additive。

import?numpy?as?np
from?pandas?import?read_csv
import?matplotlib.pyplot?as?plt
from?statsmodels.tsa.seasonal?import?seasonal_decompose
from?pylab?import?rcParams

elecequip?=?read_csv(r"C:/Users/datas/python/data/elecequip.csv")
result?=?seasonal_decompose(np.array(elecequip),?model='multiplicative',?freq=4)

rcParams['figure.figsize']?=?10,?5
result.plot()
pyplot.figure(figsize=(40,10))
pyplot.show()

上圖的第一行代表實(shí)際數(shù)據(jù)，底部的三行顯示了三個(gè)要素。這三個(gè)要素累加之后即可以獲得原始數(shù)據(jù)。第二個(gè)樣本集代表趨勢性，第三個(gè)樣本集代表季節(jié)性。如果我們考慮完整的時(shí)間范圍，你會(huì)看到趨勢一直在變化，并且在波動(dòng)。對于季節(jié)性，很明顯，在規(guī)律的時(shí)間間隔之后可以看到峰值。

06 如何獲得季節(jié)性調(diào)整值？

對于可加性模型，可以通過y（t）– s（t）獲得季節(jié)性調(diào)整后的值，對于乘法數(shù)據(jù)，可以使用y（t）/ s（t）來調(diào)整值。

如果你正想問為什么我們需要季節(jié)性調(diào)整后的數(shù)據(jù)，讓我們回顧一下剛才討論過的有關(guān)美國失業(yè)率的示例。因此，如果季節(jié)性本身不是我們的主要關(guān)注點(diǎn)，那么季節(jié)性調(diào)整后的數(shù)據(jù)將更有用。盡管經(jīng)典方法很常見，但由于以下原因，不太建議使用它們：

其他可用于分解的更好方法是X11分解，SEAT分解或STL分解。現(xiàn)在，我們將看到如何在Python中生成它們。

與經(jīng)典法，X11和SEAT分解法相比，STL具有許多優(yōu)點(diǎn)。接下來，讓我們探討STL分解法。

07 STL分解法

STL代表使用局部加權(quán)回歸（Loess）進(jìn)行季節(jié)性和趨勢性分解。該方法對異常值具有魯棒性，可以處理任何類型的季節(jié)性。這個(gè)特性還使其成為一種通用的分解方法。使用STL時(shí)，你控制的幾件事是：

同任何其他方法一樣，STL也有其缺點(diǎn)。例如，它不能自動(dòng)處理日歷的變動(dòng)。而且，它僅提供對可加性模型的分解。但是你可以得到乘法分解。你可以首先獲取數(shù)據(jù)日志，然后通過反向傳播要素來獲取結(jié)果。但是，這超出了本文討論的范圍。

import?pandas?as?pd
import?seaborn?as?sns
import?matplotlib.pyplot?as?plt
from?statsmodels.tsa.seasonal?import?STL

elecequip?=read_csv(r"C:/Users/datas/python/data/elecequip.csv")
stl?=?STL(elecequip,?period=12,?robust=True)
res_robust?=?stl.fit()
fig?=?res_robust.plot()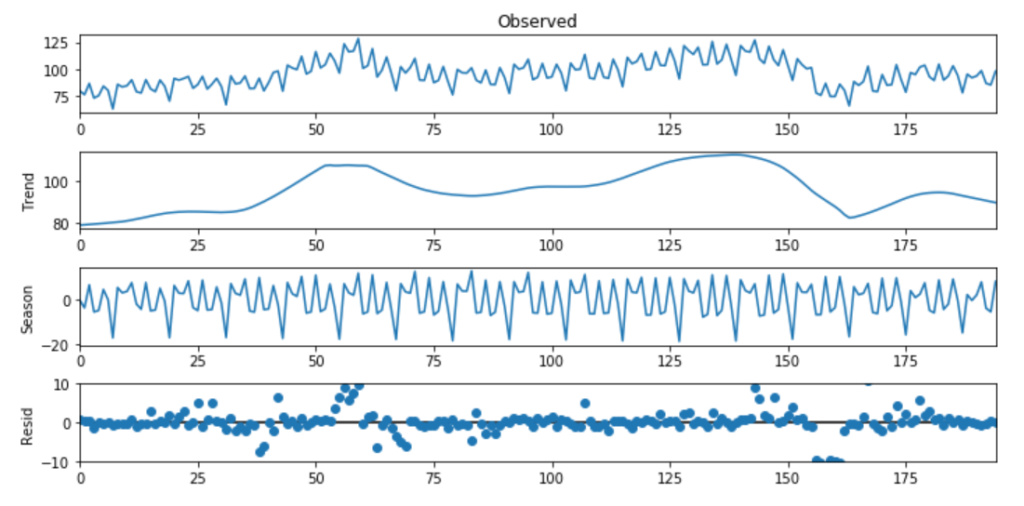

08 時(shí)間序列預(yù)測的基本方法

盡管有許多統(tǒng)計(jì)技術(shù)可用于預(yù)測時(shí)間序列數(shù)據(jù)，我們這里僅介紹可用于有效的時(shí)間序列預(yù)測的最直接、最簡單的方法。這些方法還將用作其他方法的基礎(chǔ)。

1.?Python中的簡單移動(dòng)平均（SMA）

簡單移動(dòng)平均是可以用來預(yù)測的所有技術(shù)中最簡單的一種。通過取最后N個(gè)值的平均值來計(jì)算移動(dòng)平均值。我們獲得的平均值被視為下一個(gè)時(shí)期的預(yù)測。

2. 為什么使用簡單移動(dòng)平均？

移動(dòng)平均有助于我們快速識(shí)別數(shù)據(jù)趨勢。你可以使用移動(dòng)平均值確定數(shù)據(jù)是遵循上升趨勢還是下降趨勢。它可以消除波峰波谷等不規(guī)則現(xiàn)象。這種計(jì)算移動(dòng)平均值的方法稱為尾隨移動(dòng)平均值。在下面的示例中，我們使用rolling（）函數(shù)來獲取電氣設(shè)備銷售數(shù)據(jù)的移動(dòng)平均線。

import?pandas?as?pd
from?matplotlib?import?pyplot

elecequip?=?pd.read_csv(r"C:/Users/datas/python/data/elecequip.csv")

#?Taking?moving?average?of?last?6?obs
rolling?=?elecequip.rolling(window=6)
rolling_mean?=?rolling.mean()

#?plot?the?two?series
pyplot.plot(elecequip)
pyplot.plot(rolling_mean,?color='red')
pyplot.show()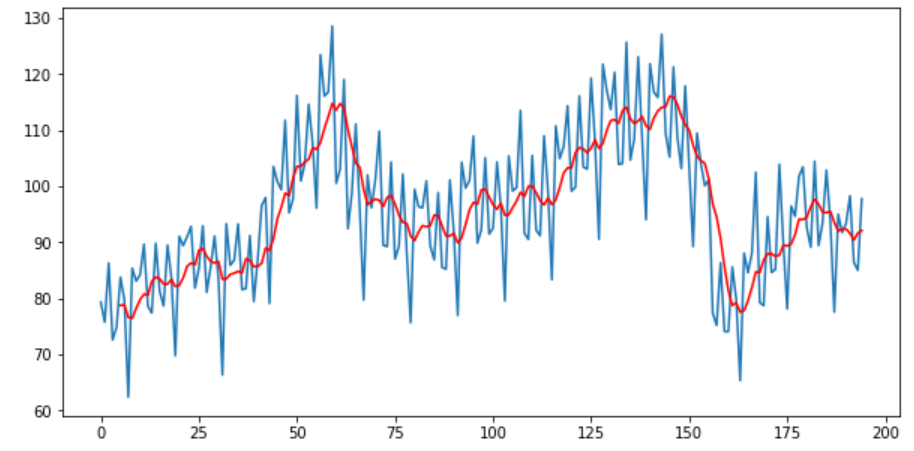

另一種方法是“中心移動(dòng)平均”。在這里將任意給定時(shí)間（t）的值計(jì)算為當(dāng)前，之前和之后的平均值。啟用center = True將提供中心移動(dòng)平均值。

elecequip["x"].rolling(window=3,?center=True).mean()

3.?Python中的加權(quán)移動(dòng)平均（WMA）

簡單移動(dòng)平均非常樸素，因?yàn)樗鼘^去的所有值給予同等的權(quán)重。但是當(dāng)假設(shè)最新數(shù)據(jù)與實(shí)際值密切相關(guān)，則對最新值賦予更多權(quán)重可能更有意義。

要計(jì)算WMA，我們要做的就是將過去的每個(gè)觀察值乘以一定的權(quán)重。例如，在6周的滾動(dòng)窗口中，我們可以將6個(gè)權(quán)重賦給最近值，將1個(gè)權(quán)重賦給最后一個(gè)值。

import?random
rand?=?[random.randint(1,?i)?for?i?in?range(100,110)]
data?=?{}
data["Sales"]?=?rand

df?=?pd.DataFrame(data)
weights?=?np.array([0.5,?0.25,?0.10])

sum_weights?=?np.sum(weights)
df['WMA']=(df['Sales']
.rolling(window=3,?center=True)
.apply(lambda?x:?np.sum(weights*x)/sum_weights,?raw=False)

)
print(df['WMA'])

4.?Python中的指數(shù)移動(dòng)平均（EMA）

在“指數(shù)移動(dòng)平均”中，隨著觀察值的增加，權(quán)重將按指數(shù)遞減。該方法通常是一種出色的平滑技術(shù)，可以從數(shù)據(jù)中消除很多噪聲，從而獲得更好的預(yù)測。

import?numpy?as?np
import?pandas?as?pd
import?matplotlib.pyplot?as?plt
from?statsmodels.tsa.api?import?ExponentialSmoothing

EMA_fit?=?ExponentialSmoothing(elecequip,?seasonal_periods=12,?trend='add',?seasonal='add').fit(use_boxcox=True)
fcast3?=?EMA_fit.forecast(12)


ax?=?elecequip.plot(figsize=(10,6),?marker='o',?color='black',?title="Forecasts?from?Exponential?Smoothing"?)
ax.set_ylabel("Electrical?Equipment")
ax.set_xlabel("Index")

#?For?plotting?fitted?values
#?EMA_fit.fittedvalues.plot(ax=ax,?style='--',?color='red')

EMA_fit.forecast(12).rename('EMS?Forecast').plot(ax=ax,?style='--',
?marker='o',?color='blue',?legend=True)

該方法具有以下兩種變體：?

1. 簡單指數(shù)平滑–如果時(shí)間序列數(shù)據(jù)是具有恒定方差且沒有季節(jié)性的可加性模型，則可以使用簡單指數(shù)平滑來進(jìn)行短期預(yù)測。
2. Holt指數(shù)平滑法–如果時(shí)間序列是趨勢增加或減少且沒有季節(jié)性的可加性模型，則可以使用Holt指數(shù)平滑法進(jìn)行短期預(yù)測。

import?numpy?as?np
import?pandas?as?pd
import?matplotlib.pyplot?as?plt
from?statsmodels.tsa.api?import?SimpleExpSmoothing,?Holt

劃重點(diǎn)??

干貨直達(dá)??

• 手把手教你用ECharts畫柱狀圖
  

• 人工智能三大關(guān)鍵能力，終于有人講明白了
  

• 數(shù)據(jù)缺失值的3種處理方式，終于有人講明白了
  

• 5G時(shí)代不可或缺的關(guān)鍵技術(shù)：詳解邊緣計(jì)算參考架構(gòu)3.0

更多精彩??